基于残差修正GM（1，1）模型的采空区残余变形预测研究

薛永安，冀 哲，张文志

（1.河南理工大学 测绘与国土信息工程学院，河南 焦作 454000；2.太原理工大学 矿业工程学院，山西 太原 030024；3.河南省采空区场地生态修复与建设技术工程研究中心，河南 焦作 454000）

地下矿产采出后，开采区周围岩土体的原始应力平衡状态被破坏，岩土体上出现位移与变形[1]，对采煤沉陷区土地再利用和建（构）筑物安全运维带来了安全隐患。剩余变形是采空区地表移动变形基本稳定后的变形，也称为采煤沉陷区的残余变形[2]。目前，针对残余变形预计的研究众多[3-9]，大多基于开采沉陷的概率积分法进行修正[6-10]，并有残余下沉系数的计算[11]，同时有基于非线性数学模型的预测方法[4,12]和组合预测模型[13-14]被实践验证，对开展残余变形精准预测模型研究具有较好的参考价值。然而，采空区残余沉降呈非线性特点，且时间跨度大、变形量小，一般很少开展长时间序列化监测，样本数据偏少，给预测模型建立及验证带来了一定的困难。灰色系统模型是目前解决非线性问题的重要数学方法之一[15]，因其建模时所需数据样本较少、计算简单且预测精度较好等特点而被广泛研究与应用[16-18]，基于灰色系统模型开展采空区地表残余变形预测具有方法可行性。灰色系统理论体系中，GM（1，1）模型属于灰色预测的核心模型，针对GM（1，1）模型的改进、优化等预测应用较多，主要从数据预处理[19]、残差修正[20]、灰色模型背景值优化[21]、综合改进[22]等角度进行了探索，研究成果及行业应用较为丰富，为灰色系统理论在残余变形预测领域的深入应用提供了理论与实践参考。基于上述研究现状，从预测结果残差修正入手，开展针对GM（1，1）模型的后改进研究，对比一元二次多项式拟合修正GM（1，1）0模型和正化残差后一元二次多项式拟合修正GM（1，1）1模型的预测精度，为老采空区残余变形精准预测模型构建进行初步探索。

1 残差修正GM（1，1）预测模型

1.1 灰色GM（1，1）模型

灰色系统模型相比较其它预测模型所需建模信息量小，但预测精度较高，且越靠近预测时间段时预测精度越高。目前，依据不同目的所建立的灰色系统预测模型较多，GM（1，1）是其中较常使用的预测模型之一，主要针对1 个变量建模进行一阶灰色预测[23]。

设非负离散数据序列x(0)为：

式中：n 为序列长度。

对x(0)进行一次累加生成，即可得到1 个生成序列x(1)＝｛x(1)（1），x(1)（2），…，x(1)（n）｝，对此累加生成序列建立一阶微分方程（GM（1，1）模型）：

式中：a、b 为灰参数；t 为时间。

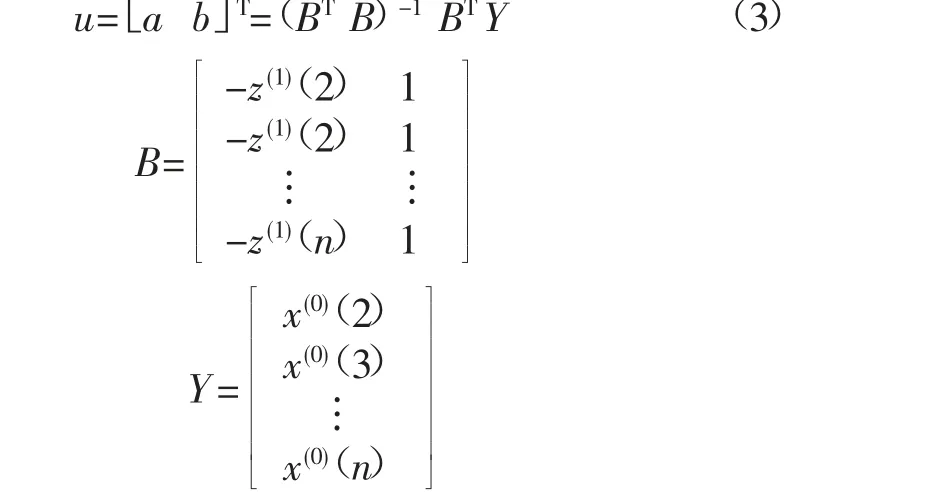
求出u 后代入式（2），并做累减生成，可得到还原后的原始数据序列预测值x(0)（k）：

当k＜n 时，x(0)（k）为模型拟合值；当k=n 时，x(0)（k）为模型滤波值；当k＞n 时，为x(0)（k）模型预测值[23]。

1.2 监测数据序列插值

GM（1，1）模型是针对等间距数据序列的预测模型，然而受各种因素影响，实际获取到的变形监测数据序列一般都是不等间距[24]，限制了GM（1，1）模型的应用场景及预测有效性。针对数据不等间距的问题，学者们从不同的角度开展了研究与模型改进[25-27]，其中，插值法通过对原始非等间距监测数据进行等距处理使其等间距化，然后按照等间距数据序列进行建模，最后将数据还原[28]。常用的插值方法包括加权平均法、三次样条法、拉格朗日法、切比雪夫多项式法和牛顿法，经过对比实验，综合考虑插值精度和构造简便性等因素，选用牛顿插值法作为等间距监测数据序列的构造方法。

设x0，x1，…，xn为n+1 个插值节点，且x≠xi（i＝0，1，2，…，n），牛顿插值多项式的表达式f（x）为[29]：

式中：Nn（x）为牛顿插值公式；Rn（x）为牛顿插值多项式余项。

Nn（x）与Rn（x）的表达式分别为：

1.3 残差非线性拟合修正

任何1 个复杂的曲线都可以采用1 个多项式来进行描述，也就是说多项式可以逼近任意函数。基于GM（1，1）预测模型所建立的残差曲线，通过预测值与观测值确定的残差序列，使残差序列的平方和最小，此时的曲线就是利用多项式所建立的残差非线性拟合曲线，利用该残差曲线修正所有的预测值，从而达到提升预测精度的目的。

针对非线性特征明显的采空区地表残余变形GM（1，1）模型预测值残差序列，采用一元二次多项式拟合方式对残差值进行拟合修正，改善GM（1，1）模型的预测精度。

设GM（1，1）模型预测值残差序列为：

式中：ε(0)（k）为观测值x(0)（k）与GM（1，1）模型预测值x^(0)（k）之间的残差；k=2，3，…，n。

对残差序列的一元m 次多项式拟合函数如下[22]：

式中：k=1，2，…，n-1；m∈［2，n/3］，cp为一元m次多项式系数。

经对比实验后取m=2，采用最小二乘原理通过迭代法求解cp值，将得到系数值代入式（9），则残差修正预测值的一元二次多项式如下：

式中：c0、c1、c2为系数。

利用式（10）求得的ε^(0)（k）对ε(0)（k）进行修正，修正公式如下：

1.4 正化残差非线性拟合修正

预测值残差序列的符号很难保持一致性，而是在正负之间跳跃，使得对符号一致性有要求的数学模型难以适用。为了提升残差修正效果，先构建原始残差值的符号矩阵B，记录残差值的正负号。

其中：

将残差序列进行正化（符号一致为正）处理，构建改进正化残差序列ε+(0)（k）：

再对正化后的残差序列利用公式（10）进行拟合，得到残差修正值ε^+(0)（k）。

将得到的残差修正值根据原始残差的符号进行正负恢复，令：

其中：

最后用ε^(1)（k）补偿残差ε(0)（k），预测值x^ε(0)（k）计算公式如下：

2 模型等级与预测精度评价

2.1 模型等级评价

GM（1，1）模型检验通常以C、P 值判定，C、P 值的计算方法见文献［23］，根据C、P 值的计算结果判定GM（1，1）模型精度等级，GM（1，1）模型精度等级评价标准见表1[23]，总体评价时一般取C 值与P 值评价结果中最高等级为模型等级。以C、P 值组合评价GM（1，1）拟合模型的精度等级。

表1 GM（1，1）模型精度等级评价标准Table 1 Accuracy grade evaluation standard of GM（1，1）model

2.2 预测精度评价

一般常用预测误差平方和、均方误差、平均绝对误差、平均绝对百分比误差和均方百分比误差5 种指标进行预测模型的预测精度评价[13]，选择均方误差和平均绝对百分比误差组合评价GM（1，1）模型的预测精度，具体计算方法如下[13]：

1）均方误差（MSE）。以预测误差值平方和取平方根的平均值MSE 作为评价指标，计算公式如下：

式中：N 为观测次数；xt（t=1，2，…，N）为观测值；x^t为xt的预测值。

2）平均绝对百分比误差（MAPE）。MAPE 以预测值相对误差绝对值的平均值作为评价指标，计算公式如下：

均方误差和平均绝对百分比误差的值越大，预测精度越低，预测模型也越差，反之亦然。

3 试例验证

3.1 试验数据

3.1.1 试验1（等间距数据序列）

收集到陕西省北部某煤矿52406 工作面开采后地表沉降监测数据集，观测方法为三角高程测量，选取地表沉降趋于稳定后的15 期实测累计沉降观测值为数据源，以A09 号监测点开展等间距数据序列残差修正GM（1，1）模型的采空区地表残余变形预测及结果验证。A09 号监测点等间距累计下沉观测值见表2。

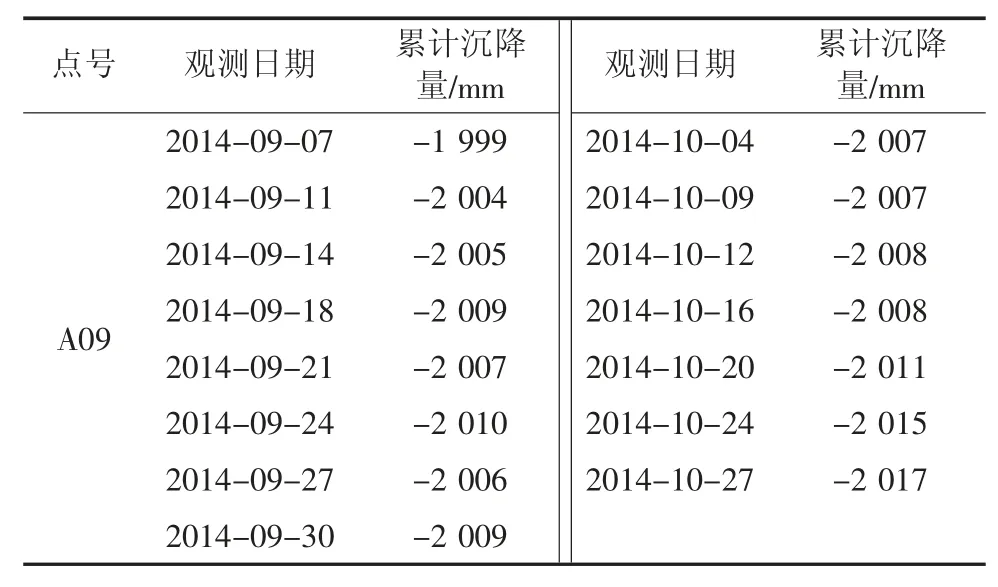
表2 A09 号监测点等间距累计下沉观测值Table 2 Accumulated observation values of A09 with equal time distance

A09 号点共有15 期近似等间距沉降观测数据，选取该数据中的前11 期数据进行GM（1，1）模型拟合，对后4 期数据进行预测，并对比观测值分析预测精度。

3.1.2 试验2（非等间距数据序列）

收集到山西省北部某大型输水线路下伏老采空区地表沉降监测数据集，观测方法为二等水准测量，选取19 期实测累计沉降观测值为数据源，以ⅡR1—1 号监测点开展非等间距数据序列残差修正GM（1，1）模型的采空区地表残余变形预测及结果的验证。ⅡR1-1 号监测点非等间距累计下沉观测值见表3。

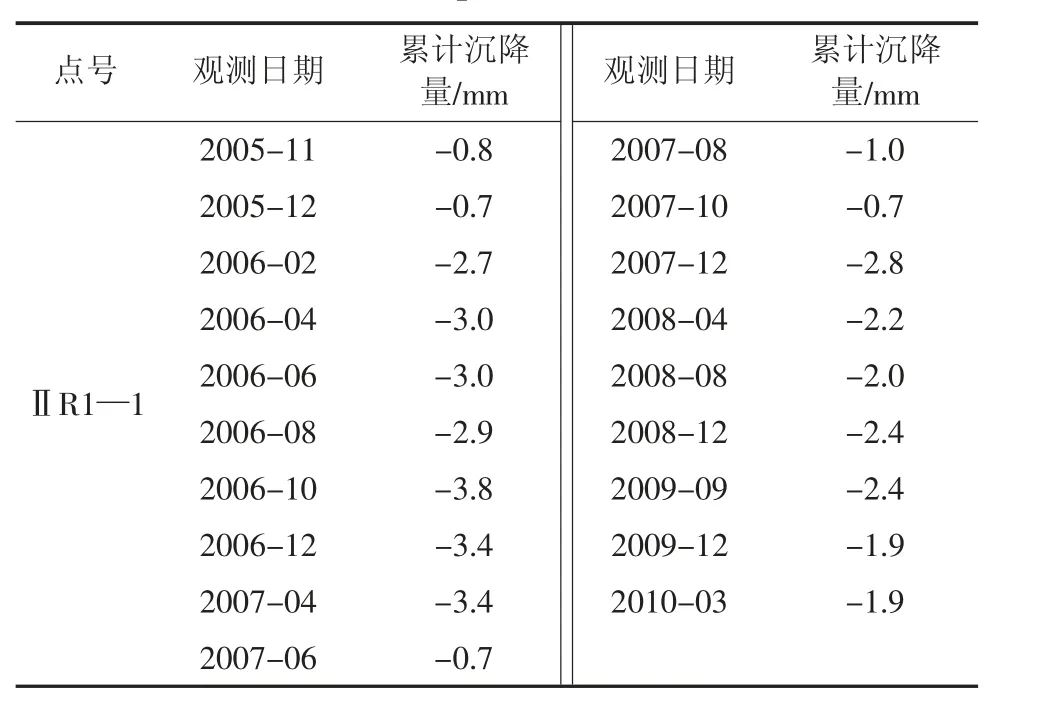
表3 ⅡR1—1 号监测点非等间距累计下沉观测值Table 3 Accumulated observation values of ⅡR1—1 with non- equal time distance

ⅡR1—1 号点共有19 期非等间距沉降观测数据，首先对非等间距监测数据按月进行牛顿插值法内插，获取到等间距监测数据共53 期，然后选取该数据序列中的前47 期数据进行GM（1，1）模型拟合，对后6 期数据进行预测，并对比内插等间距监测数据分析预测精度。

3.2 残差修正GM（1，1）模型预测结果

记传统GM（1，1）预测模型为GM（1，1），采用非线性改正进行GM（1，1）模型预测结果残差修正的模型为GM（1，1）0，采用正化残差非线性改正进行GM（1，1）模型预测结果残差修正的模型为GM（1，1）1。

分别采用GM（1，1）、GM（1，1）0和GM（1，1）1模型对试验1 与试验2，数据进行预测3 种模型在A09、ⅡR1—1 号监测点的拟合与预测结果对比见表4，3 种模型预测残差对比如图1。

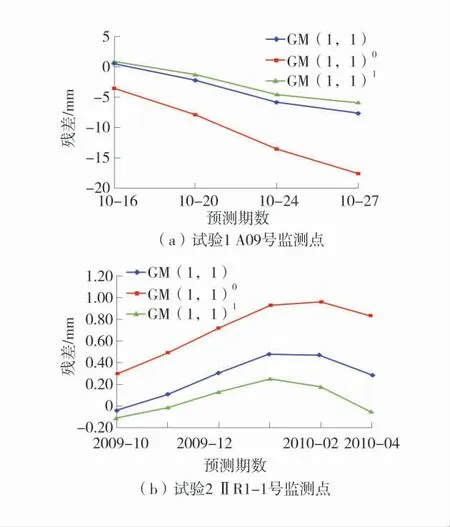
图1 3 种模型预测值残差对比图Fig.1 Residuals comparison of predicted values of the three models

表4 3 种模型预测结果对比表Table 4 Comparison of prediction results of three models

由表4 可知：GM（1，1）模型在A09 点与ⅡR1—1 点的拟合平均相对误差分别为0.07%和44.86%，GM（1，1）0模型分别为0.06%和42.58%，GM（1，1）1模型分别为0.03%和23.26%；GM（1，1）、GM（1，1）0、GM（1，1）1模型在A09 点的拟合值残差中误差分别为1.62、1.36、0.71，而在ⅡR1—1 点的预测值残差中误差分别为0.81、0.80、0.42。显然，通过对GM（1，1）模型的拟合结果进行残差修正的GM（1，1）0模型一定程度上提升了模型精度，而正化残差修正的GM（1，1）1模型精度则较GM（1，1）0模型进一步提升。

由表4 可知：GM（1，1）模型在A09 点与ⅡR1—1 点的预测平均相对误差分别为0.20%和15.38%，GM（1，1）0模型分别为0.53%和37.99%，GM（1，1）1模型分别为0.16%和6.80%；GM（1，1）、GM（1，1）0、GM（1，1）1模型在A09 点的预测值残差中误差分别为4.95、11.95、3.85，而在ⅡR1—1 点的预测值残差中误差分别为0.32、0.75、0.15。显然，试验1 与试验2 中，GM（1，1）1模型的预测平均相对误差和残差中误差总体较GM（1，1）0和GM（1，1）模型都小，预测效果改善明显。

图1 显示：试验1 与试验2 中3 种模型的预测值残差趋势一致，GM（1，1）1模型的预测值残差均最小，GM（1，1）模型次之，GM（1，1）0模型的预测值残差均最大。综合表4 中拟合平均相对误差、拟合残差中误差、预测平均相对误差和预测残差中误差，可以看出，采用一元二次多项式拟合方式对残差值进行拟合修正可以提升GM（1，1）模型拟合的精度，但是模型的预测精度没有提升，且出现了大幅降低，而采用正化残差非线性拟合修正则显著提升了GM（1，1）模型在拟合与预测中的精度。

3.3 模型检验与预测精度

计算得到各监测点在3 种预测模型中拟合值的C、P 值和预测值的MSE、MAPE 值，模型等级与预测精度评价见表5。

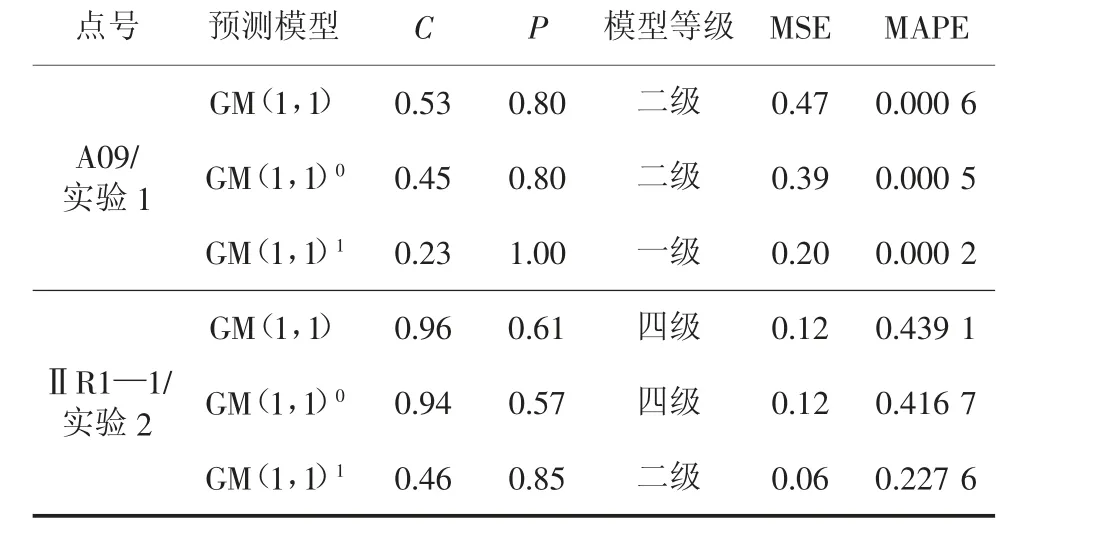
表5 模型等级与预测精度评价Table 5 Evaluation of model grade and prediction accuracy

由表5 可知：GM（1，1）模型和GM（1，1）0模型在A09 点、ⅡR1—1 点的模型等级均相同，分别为二级、四级，而GM（1，1）1模型在A09 点、ⅡR1—1点的模型等级分别为一级和二级；对比C、P 值可以看出，试验1 中，模型等级由高到低的顺序依次是GM（1，1）1模型＞GM（1，1）0模型＞GM（1，1）模型；试验2 中，GM（1，1）1模型的模型等级最高（二级），GM（1，1）模型和GM（1，1）0模型则基本一致，均为四级（不合格），通过正化残差非线性拟合修正实现了GM（1，1）模型的合格化，且模型等级提升为二级（合格）。

由MSE、MAPE 值可以看出，GM（1，1）1模型在A09 点和ⅡR1—1 点的预测精度显著高于GM（1，1）0和GM（1，1）模型。

3.4 讨 论

1）由表4 可以看出，试验1 与试验2 中，GM（1，1）0、GM（1，1）1模型的拟合精度均较GM（1，1）模型有所提升，但GM（1，1）1模型拟合精度增益更为明显。其中，GM（1，1）1模型在A09 点拟合结果残差的中误差值较GM（1，1）0、GM（1，1）模型分别降低了48.25%、56.73%，而在ⅡR1—1 点则分别降低了51.85%、52.44%，降幅均达50%左右，对提升GM（1，1）模型预测能力提供了基础保障。显然，GM（1，1）1模型相比其它2 种模型更适用于煤矿采空区地表残余变形预测。

2）由表5 可以看出，GM（1，1）0模型较GM（1，1）模型预测精度提升不明显，但GM（1，1）1模型较GM（1，1）模型预测精度则提升较大。其中，GM（1，1）1模型在A09 点预测精度的MSE 值较GM（1，1）0、GM（1，1）模型分别降低了48.72%、57.45%，MAPE 值分别降低了60.00%、66.67%。而在ⅡR1—1 点预测精度的MSE 值分别降低了50.00%、50.00%，MAPE 值分别降低了45.38%、48.17%。由此表明，对拟合结果残差先进行正化处理后再进行非线性拟合修正比直接进行非线性拟合修正后预测的效果要好。

3）残差修正模型大多对残差序列有符号要求，目前，对GM（1，1）模型的残差修正多采用GM（1，1）模型进行，这种修正方式显然未考虑残差符号各异性特征。本研究采用非线性多项式拟合作为残差修正模型，对GM（1，1）模型预测结果进行正化残差非线性修正，预测精度显著提高，且该方法对残差序列无特殊要求，适用范围更广，为变形预测模型后改进研究提供了参考。

4 结 语

1）以残差修正方式对GM（1，1）模型进行后改进处理，试例验证的平均相对误差、残差中误差、C、P、MSE 和MAPE 值统计结果一致表明，残差修正对提升GM（1，1）模型预测精度具有明显的增益，是后改进GM（1，1）变形预测模型的有效方式。

2）采用正化残差多项式拟合修正的GM（1，1）1模型对提升GM（1，1）模型预测精度具有显著作用，且该模型不受残差符号统一性的限制，可直接针对预测值残差序列进行拟合修正，预测精度进一步提升，模型适用范围更广，较GM（1，1）模型和直接采用多项式拟合修正残差的GM（1，1）0模型更适用于煤矿采空区地表残余变形预测。

3）C、P、MSE 和MAPE 值的评价结果一致，模型等级高的预测模型其预测精度高，反之亦然，这4 种指标互为补充与支撑，是评价灰色系统模型预测能力的合理评价指标组合。

本研究的工作对老采空区残余变形预测模型研究具有一定的参考价值，但本研究仅采用了后改进处理方式，未对观测数据序列进行前改进处理，如卡尔曼滤波、粗差探测与剔除等，今后应就此问题继续开展研究，推进综合“前+后”改进的GM（1，1）模型在采空区地表残余变形预测中的应用，推动非线性系统理论变形预测方法体系发展。