考虑风光荷时序波动特性的配电网投资策略多目标优化
樊晓伟,王瑞妙,朱小军,姚 龙,周兴华,张 晓,4
(1.国网重庆市电力公司,重庆 400014;2.国网重庆市电力公司电力科学研究院,重庆 401123;3.北京中恒博瑞数字电力科技有限公司,北京 100085;4.华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引言
随着国家“碳达峰”、“碳中和”目标的提出,电力行业加快构建以新能源为主体的新型电力系统。然而风、光等分布式电源发电出力具有较强的随机波动性,随着渗透率快速提升对电网安全稳定运行造成较大影响。如何应对风、光等分布式电源的时序波动特性已经成为配电网规划投资领域关注的焦点。
针对源-荷不确定性问题,文献[1]提出了综合考虑配电网运行经济性和电压良好分布的基于分布式电源选址定容的配网降损方法。文献[2],[3]提出计及时序性与相关性的分布式光伏长短期规划,但是未考虑风电、光伏发电互补。文献[4]提出“源-储-荷”多目标优化配置方法。文献[5]提出聚类网架拓扑的配电网分布式电源规划方法。文献[6]提出基于模糊理论含分布式电源的配电网网架规划方法,但未考虑风光荷时序波动特性。文献[7]提出考虑分布式电源时序特性及电动汽车时空特性的配电网规划,但未考虑电网安全稳定运行。
风电、光伏等分布式电源出力和不同类型的常规负荷大小具有明显的时序特性,而常用的恒定功率模型、概率模型都无法准确体现这一特点。本文构建了风力、光伏发电出力概率模型,应用蒙特卡洛法对其发电出力和负荷进行模拟仿真,生成大量场景;引入改进K中心点聚类算法缩减场景;从各典型场景发生概率出发,以光伏、风力电站投资效益和配电网安全稳定运行为目标,采用改进多目标遗传算法求解光伏、风力电站最优安装位置和容量。最后,利用IEEE33节点配电系统进行算例分析,验证了所提方法的可行性。
1 风光荷出力时序特性建模
光伏、风力等分布式电源发电功率与气象条件紧密相关。风力发电功率主要受风速影响,光伏发电功率则与太阳光照强度紧密相关。
根据大量风速历史数据统计分析,一定时段内风速大致服从双参数Weibull分布,其概率密度函数如式(1)所示。

式中:v为风速;k,c为Weibull分布的两个参数;vμ,vδ分 别 为 统 计 时 段 风 速 的 均 值、标 准 差。
风力发电功率PDWG与风速v的关系如下所示:

式中:vci为切入风速;vco为切出风速;vcr为额定风速。
根据大量光伏历史数据统计分析,一定时段内太阳光照强度大致服从Beta分布,其概率密度函数为

式中:s为实际光照强度;smax为最大光照强度;s/smax为晴空因子;α,β为Beta分布的两个参数。

式中:sμ,sδ分别为统计时段历史晴空因子的均值、标准差。
光伏发电功率PPV与光照强度s的关系为

式中:sr为额定光照强度;PPV_r为光伏发电额定出力。
根据大量电力负荷历史数据统计分析,一定时段内电力负荷大致服从截断Gaussian分布,其概率密度函数为

式 中:PL为 负 荷 功 率;Pup,Plow分 别 为 负 荷 的 上、下限值;Pμ,Pδ分 别为统计 时段负 荷数据的 均值、标准 差[7]。
2 基于改进K中心聚类的场景缩减
根据某地区风速、光照强度历史数据以及居民负荷、商业负荷数据,计算得出风光荷概率模型参数。应用蒙特卡洛方法,生成风光荷大规模时序仿真数据。由于大规模时序数据计算复杂度较高,因此需要对风电、光伏出力场景进行削减,以精简数据、减少计算量。
聚类法通过将具有一定相似度的曲线聚为一类进行场景缩减。文献[8]采用k-means对全年风电、光伏、负荷数据进行聚类,用于电力系统中长期规划。本文采用改进的K中心点聚类算法将风、光、荷蒙特卡洛仿真数据进行有效聚类,在保证风电、光伏、负荷分布特性的前提下减少场景数量。
2.1 风光荷曲线距离度量方法
在聚类分析中,需要评估各对象之间相似或不相似程度。距离是评估各对象之间相似程度常用的计算方法,距离越小,相似程度越高。用户负荷曲线作为一种高维数值属性对象,选择一种合适的距离计算方法是聚类分析的关键。
假 设 两 条 时 间 序 列A={a1,…,ai,…,am}和B={b1,…,bj,…,bn},m和n分 别 为A和B的 长 度,动 态 时 间 弯 曲(Dynamic Time Warping,DTW)距离 构 造 一 个m×n的 矩 阵M,元 素M(i,j)为ai与bj之间的距离。在矩阵M中寻找一条使两条序列间累 积 距 离 最 小 的 弯 曲 路 径W={w1,…,wi,…,wK},并且满足以下约束:
①有 界 约 束:max(m,n)≤K≤m+n-1;
②边 界 约 束:元 素w1=M(1,1),wK=M(m,n)分别为弯曲路径起点和终点;
③连 续 性 约 束:给 定 元 素wt=M(i,j),其 相 邻元 素wt-1=M(i′,j′)需 满 足i-i′≤1,j-j′≤1,即 弯 曲路径元素是相邻的;
④单 调 性 约 束:给 定 元 素wt=M(i,j),其 相 邻元 素wt-1=M(i′,j′)需 满 足i-i′≥0,j-j′≥0。
矩阵M中存在多条满足上述约束条件的弯曲路径,而时间序列A和B的DTW距离是最小的弯曲路径。弯曲路径采用动态规划算法求解,其最优解子结构为

式 中:i=1,2,…,m;j=1,2,…,n;d(0,0)=0,d(i,0)=(0,j)=+∞。
因此,上述时间序列A和B的DTW距离为Ddtw(A,B)=d(m,n)。相 比 于 欧 氏 距 离 和 曼 哈 顿 距离,DTW距离不仅能反映两个序列之间的距离,而且能反映二者之间的变化趋势[9]~[11]。
图1为额定功率为2000kW光伏发电典型日的出力曲线。典型日1出力曲线与其它几个典型日出力曲线的欧氏距离、DTW距离计算结果如表1所示。从图1可以看出,典型日1出力曲线与典型日6出力曲线相似性最差,与典型日4出力曲线比较相似。从表1可以看出:典型日1出力曲线与典型日6出力曲线的欧氏距离较小、DTW距离较大;典型日1出力曲线与典型日4出力曲线的欧氏距离较大、DTW距离较小。因此,DTW距离能够捕获日功率发电曲线之间的相似度。
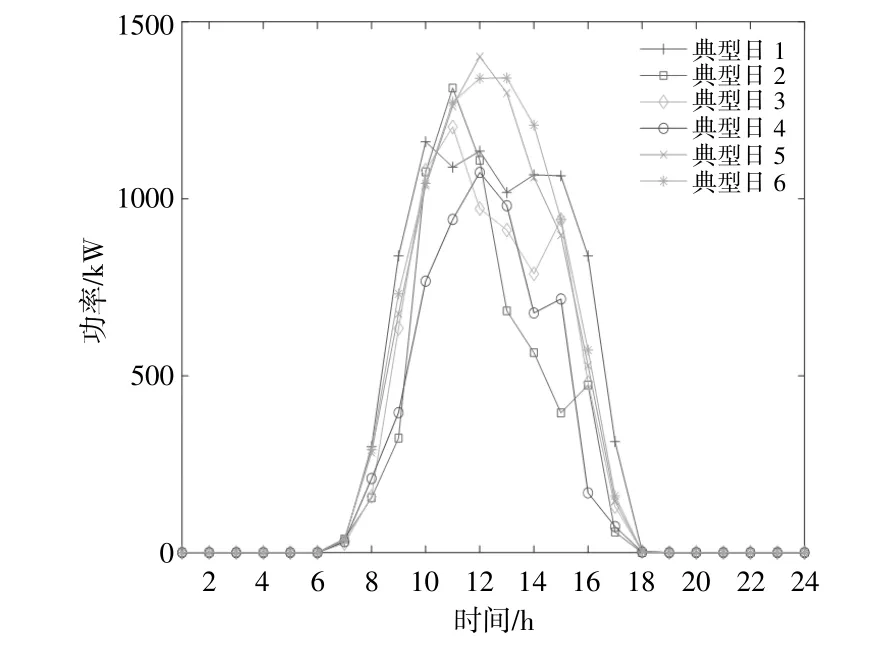
图1 光伏发电日出力曲线Fig.1 Daily power curve of photovoltaic generation
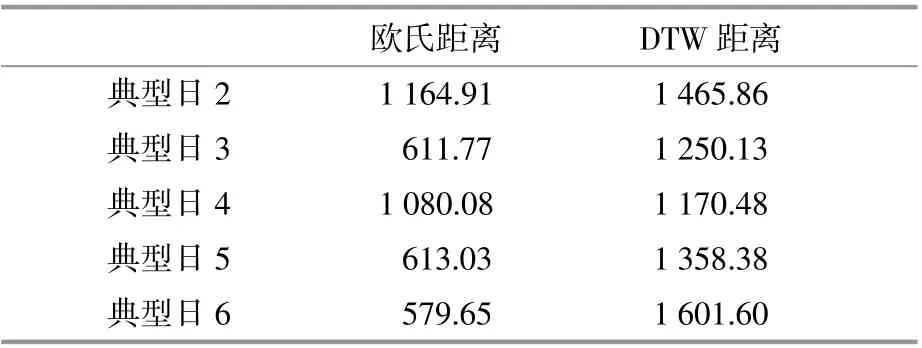
表1 典型日1与其它典型日出力曲线距离Table1 Distance between typical daily1and other typical daily output curves
2.2 风光荷仿真场景缩减
在风光荷仿真场景缩减时,首先采用DTW距离计算不同曲线之间的相似度,构建曲线相似度矩阵;然后采用K中心点聚类算法开展风力发电、光伏发电、用户负荷曲线聚类分析,各个聚类簇的中心点即为风光荷的典型模式[12],[13]。
3 基于多目标遗传算法的分布式电源投资策略
本文采用改进的K中心点聚类算法将大规模的风电、光伏出力曲线数据和负荷曲线数据缩减为几种典型场景。风、光、荷各个典型场景联合组成各种典型风光荷综合应用场景,所有场景共同刻画了真实环境下风光荷运行的随机性和间歇性。
3.1 目标函数
在分布式电源接入配电网投资规划中,不仅要考虑电网公司光伏、风电场投资效益,也要考虑配电网安全稳定经济运行。
光伏、风电场投资效益是指除了设备投资费用、运行维护费用以外的电站发电售电收益。下面以光伏为例,计算式如下:

式中:F1为电站投资回报率;Seg为电站发电售电收益;ΔCloss为分布式发电电网节能降损效益;CPV为电站设备投资安装费用;Cyun为电站设备运维费用;Pi为第i个光伏负荷联合时序场景发生概率;m为光伏负荷联合时序场景数量。
分布式电源设备投资安装费用、运维费用分别为
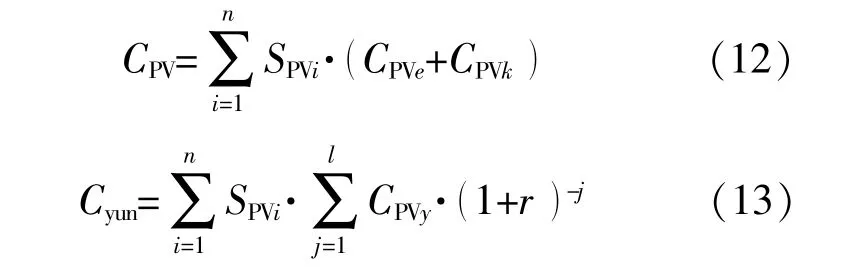
式中:n为光伏接入电网的节点数量;SPVi为i节点光伏安装容量;CPVe为单位容量光伏的设备成本;CPVk为单位容量光伏的安装成本;CPVy为每年单位容量光伏的运维费用;l为光伏的投资回收期;r为贴现率。
分布式电源设备投资回收期内发电售电收益为

式中:Ji为节点i的售电价;Qij为节点i第j年的发电量。
分布式发电电网节能降损效益为

式 中:Jbuy为 上 网 电 价 购 电 价 ;Qloss,QlossPV分 别 为 光伏安装前、后配电网每年的电网损耗。
节点电压偏差是配电网安全稳定运行的重要指标,节点电压偏差的目标函数如下:

式中:Vij为节点i在j时刻的实际电压;V′为额定电压;t为电压数据采集时刻数量。
3.2 约束条件

式中:PGi,QGi分别为节点i的发电有功功率、无功功率;PDGi,QDGi分别为节点i的分布式电源有功功率、无功功率;PLi,QLi分别为节点i的负荷有功功率、无 功 功 率;Ui,Uj分 别 为 支 路 节 点i和j的 电 压幅值;θij为以i和j为节点的支路电压相角差;Gij,Bij分别为支路的电导、电纳。
②不等式约束条件线路有功功率约束:

式中:Pi为支路i的有功功率;Pimax为支路i允许的最大功率。
分布式电源运行约束:

式 中 :PDGi,min,PDGi,max分 别 为 节 点i的DG接 入 最小、最大有功功率;PDGi为节点i的DG接入有功功率。
节点电压约束:

式 中:Vi为 节 点i的 实 际 电 压;Vimin,Vimax分 别 为 节点i电压的下限、上限。
光伏安装总容量约束:

式中:n为光伏接入电网的节点个数;SPVi为节点i的光伏安装容量;u为规划地区配电网用电负荷数;PLj为j节点的用电负荷功率;Rupper为规划地区分布式光伏容量渗透率的上限。
3.3 基于改进多目标遗传算法的配电网投资策略
与单目标优化不同,多目标优化问题通常存在一组非劣解,即帕累托最优解集。
定 义:xu,xv∈X是 两 个 可 行 解,xv相 比xu是 支配的,当且仅当:

式中:m为目标函数数量。
对于解空间X中的一个可行解xk,如果其他的任意一个可行解均不能支配xk,那么xk为该问题的帕累托最优解或者非支配解。解空间所有的帕累托最优解构成了帕累托最优解集。
非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm,NSGA)改进了遗传算法中适应度函数值的求取方法,使之可以处理多目标优化问题。在改进NSGA的基础上,NSGA-II采用快速非支配排序算法,通过拥挤度策略保证种群的多样性;同时引入精英策略,将父代种群与子代种群共 同 竞 争 得 到 下 一 代 种 群[14]~[17]。
在NSGA-II寻优过程中,如果非支配解数量超过规定数量,则需要筛选。拥挤度策略考虑非支配解之间的密集程度,当拥挤度距离越大时,该解保留下来的概率越大。
非支配解xk拥挤度距离D(xk)的计算式如下所示:

式 中 :m为 目 标 函 数 数 量 ;fq(xj)和fq(xi)为第q个目标上距离xk最近的两个非支配解;max(fq)-min(fq)为 整 个 非 支 配 解 在 第q个 目 标 上的最长距离。
但是上述拥挤度策略只计算一次拥挤度距离,存在一定的局限性,如果拥挤距离较小的多个非支配解集中在一个区域,那么这些解均将被删除。为此,本文提出了一种动态调整拥挤距离的方法,计算过程如下。
①计算相邻两个非支配解之间的距离。假设有n个 非 支 配 解,第k个 解[k∈(2,n-1)]和 第k+1个解之间的距离为

式 中:fq(k),fq(k+1)分 别 为 第k个、第k+1个 解 在第q个 目 标 上 的 函 数 值;max(fq),min(fq)分 别 为第q个目标函数的最大值、最小值。
②找 到 最 小 距 离D(k,k+1),比 较D(k-1,k)与D(k,k+1),若D(k-1,k)小,则 淘 汰xk,否 则 淘汰xk+1。
③更新相邻两个非支配解之间的距离。
④判断是否满足需要非支配解的数目。若不满足,则返回②,否则终止。
改进多目标遗传算法配电网投资策略的主要步骤如图2所示。

图2 多目标遗传算法配电网投资策略Fig.2 Investment strategy of distribution network based on multi-objective genetic algorithm
4 算例分析
本文选择IEEE33节点配电系统为算例,如图3所示,系统信息参考文献[1]。本文选择的分布式电源为风电和光伏,详细参数见文献[18]。
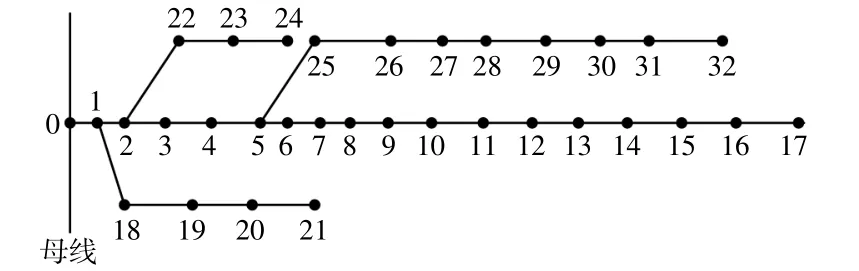
图3 IEEE33配电系统Fig.3 IEEE33distribution system
4.1 蒙特卡洛样本仿真
以日为单位,根据风力、光伏、负荷概率模型参数,应用蒙特卡洛方法对风力、光伏发电出力和负荷进行模拟仿真,生成大规模时序仿真场景。标准容量的分布式光伏出力如图4所示。

图4 光伏发电出力归一化曲线Fig.4 Normalization curve of PV power generation output
4.2 样本数据聚类分析
本文分别采用k均值和K中心点聚类算法对风力、光伏、居民负荷、商业归一化曲线数据进行聚类分析,形成不同的聚类簇和不同的样本中心点。分布式电源典型聚类场景如图5所示。

图5 分布式电源典型聚类场景Fig.5 Typical clustering scenarios of distributed power generation
居民负荷和商业负荷聚类中心点如图6所示。

图6 居民及商业负荷典型聚类场景Fig.6 Typical clustering scenarios of residential and commercial loads
4.3 节点负荷时序仿真
参照用户负荷类别1、商业负荷类别4用电规律,以IEEE33配电系统33个节点负荷为24时段平均负荷,生成为时序负荷,节点23,24,31为商业负荷,其余为居民负荷。时刻1-8各节点负荷有功功率如图7所示。

图7 33节点24时段负荷仿真Fig.7 33node load simulation of24hours
对每个时段开展潮流计算,24个时段所有线路损耗 为5.146MW·h,日 均电压 偏差 为0.051689p.u.。时刻1-8各节点电压如图8所示。末端节点在用电高峰期电压不满足要求。

图8 33节点24时段电压曲线Fig.8 33node voltage curve of node of24hours
4.4 投资规划策略对比分析
IEEE33节点配电网最大负荷为5.5MW,光伏最小单位容量为0.1MW,33个节点均可作为光伏安装位置,单节点最大光伏容量为0.3MW。1MW光伏和风电场设备投资成本均为500万元,运行维护成本均为5万元/a。光伏发电上网电价 设 为0.045万 元/(MW·h),居 民 电 价 为0.055万元/(MW·h),商 业 电 价 为0.075万 元/(MW·h)。光伏发电设备的使用寿命为20a,使用寿命期内贴现率均为0.05。
以聚类分析得到光伏发电5种典型场景,风力发电4种场景,居民负荷5种场景,商业负荷3种场景,构建300个综合时序场景。按照各综合时序场景等概率分布,构建风力、光伏发电投资规划策略。同时,分别构建只考虑风电时序特性的投资规划优化策略、只考虑光伏时序特性的投资规划策略、考虑风电+光伏时序特性的投资规划优化策略以及不考虑风光荷时序特性投资规划策略,将4种策略进行对比分析,结果如图9~12所示。

图9 光伏电站投资帕累托前沿Fig.9 Pareto frontier of photovoltaic power station investment

图10 风力电站投资帕累托前沿Fig.10 Pareto front of wind power station investment

图11 未考虑时序特性风力、光伏电站投资帕累托前沿Fig.11 Pareto front of wind power and photovoltaic power stations without considering timing characteristic
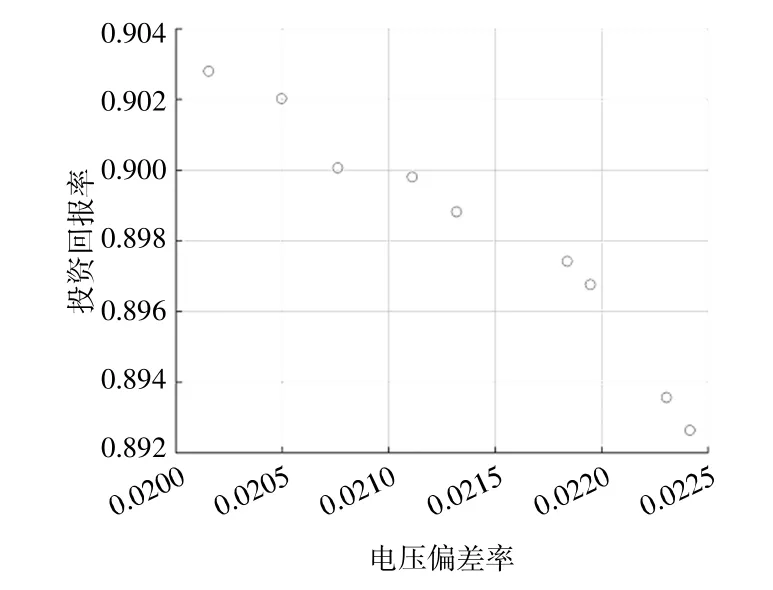
图12 考虑时序特性风力、光伏电站投资帕累托前沿Fig.12 Pareto front of wind power and photovoltaic power stations with considering timing characteristic
在电压偏差满足电能质量要求前提下,根据分布式电源电站投资回报率最大化确定最优分布式电源建设方案。上述4种投资策略下的节点平均电压偏差、投资回报率和分布式电源总容量如表2所示。

表2 4种投资策略下优化目标Table2 Optimal objectives of the four investment strategies
由表2可以看出:对比投资策略1和4,考虑风光荷时序波动特性开展分布式电源投资优化,分布式电源安装总容量更大,投资回报率和电网安全稳定性均有明显改善;对比投资策略2,3和4,考虑风力、光伏发电互补情况下开展分布式电源投资优化,在提高供电可靠性和投资回报率方面的效果优于单独风力发电和光伏发电。
充分考虑风电、光伏、电力负荷的时序波动特性,开展分布式电源投资优化,分布式电源的安装位置和容量如表3所示。

表3 考虑风光荷时序特性的DG安装位置及容量Table3 DG installation position and capacity based on the time series fluctuation of wind,photovoltaic and load
5 结论
本文考虑光伏、风力发电和负荷时序特性,利用蒙特卡洛仿真获得大量场景,并通过改进的K中心点聚类算法缩减场景,建立了计及风-光-负荷时序特性的场景概率模型;充分考虑光伏安装运维成本、售电、节能降损效益,以光伏电站投资效益最大化和电压偏差最小为目标,采用改进多目标遗传算法搜寻分布式电源最优位置和容量;并用IEEE33标准节点系统进行算例验证,风光联合发电系统在提高供电可靠性和投资回报率方面的效果优于单独的风力发电、光伏发电,风和光这两种自然资源具有明显的互补特性。

