偏航偏差角对风力机轮毂载荷的影响
冯俊恒,刘晓辉,许波峰,扶 麟,郭 敏
(1.许昌许继风电科技有限公司,河南 许昌 461000;2.河海大学,江苏 南京 211100)
0 引言
风力机通常运行在复杂的大气环境中,风速风向均在不断变化,而风轮平面法向与风速方向如果存在一定偏差,即偏航偏差角大于一定值时,风力机偏航系统就会进行对风。由于大型风力机偏航动作反应缓慢,所以风力机大部分时间都运行在存在偏航偏差角的工况下。风力机的偏航运行状态会使叶片产生较大的交变气动载荷,影响机组相关部件的载荷水平和叶片的结构变形[1],[2]。深入了解偏航偏差角状态下的风力机载荷,对优化偏航控制及保护策略具有重要意义。
有关偏航对风力机载荷影响方面的研究主要基于风洞实验和计算流体力学方法仿真。早在2001年,美国可再生能源实验室(NREL)就开展了对于Phase VI风力机的风洞实验,得到了不同偏航角度下风力机载荷随方位角变化的曲线[3]。文献[4]采用计算流体力学方法研究了MEXICO风轮在不同偏航角工况下的整体气动性能,得到了叶片截面压力系数分布、载荷系数随方位角变化规律等数据。文献[5]基于单向流固耦合分析方法对侧风条件下的小型水平轴风力机开展数值模拟,发现侧风工况下处于顺流的叶片流线分布受风向影响最大,甚至根部出现流线分流现象,同时揭示了侧风气动载荷的不对称性。文献[6]运用计算流体力学(CFD)的基本方法对NREL Phase VI风力机进行了30°偏航角范围动态偏航过程的模拟。文献[7]对NREL Phase VI风力机进行了动态偏航气动特性模拟,得到了叶片沿展向截面气动力系数载荷和有效攻角的变化规律。文献[8]将偏航模型耦合进气弹计算程序中,对某型号5MW水平轴风力机进行仿真,总结了不同偏航工况对风力机叶片变形的影响规律。
已有的研究主要利用计算流体力学方法或叶素动量编程计算方法分析风轮和叶片载荷。风力机实际运行中受到的载荷是由叶片、机舱、传动链、塔架等部件的气动特性、变形及震动耦合作用得到的结果,对于这种复杂模型,上述计算方法有一定的局限性。准确地认识风力机实际运行中的载荷表现并进行更细致的控制优化,对风力机完整建模并仿真是非常必要的。研究偏航状态下风力机的载荷时,考虑风力发电机组完整系统的仿真对进一步认识风力机运行中的载荷,改进设计和控制方案具有重要意义。
本文以某实验型3.0MW风电机组为研究对象,通过叶片气动分析和Bladed软件仿真的方法,对不同偏航偏差角下的风力机载荷进行仿真分析,以优化偏航控制和保护策略[9]。
1 风力机模型及仿真条件
本文采用的3.0MW风电机组是三叶片式双馈型风力机,其基本参数如表1所示。

表1 风力机基本参数Table1 Basic parameters of the wind turbine
该风力机叶片的设计长度为69m,叶片预弯为2.7m,重量为17.5t,塔架采用高度为87m钢筒塔架。根据以上风力机基本参数在Bladed软件中建立风力机模型(图1)。
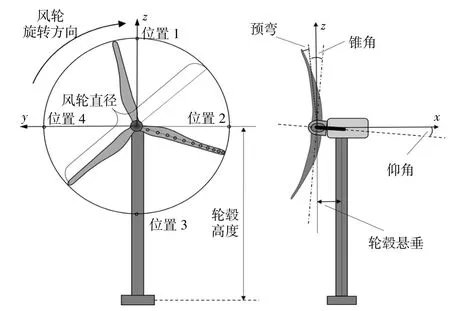
图1 风力机模型Fig.1 The turbine model
图2为该型风力机的Bladed仿真数据和测试数据对比。由图2可知,Bladed仿真的功率和塔顶弯矩与测试值的偏差均在较小范围内。说明Bladed仿真方法合理,该风力机的Bladed模型准确,能满足研究要求。

图2 仿真结果与测试结果对比Fig.2 Simulation results and measured results of the turbine
本文仿真使用的环境条件为常温环境,空气密度设为1.225kg/m3,空气粘度设为1.795×10-5kg/(m·s)。风剪切会对风轮的载荷平衡性产生影响,偏航工况下风剪切更是不能忽略的因素。本文采用风剪切指数模型,风速的分布为

式中:V(h)为实际高度处的风速;h0为参考高度;V(h0)为参考高度处的风速;h为实际高度;a为风剪切系数。
本文所研究模型中,a设置为0.2。同样要在Bladed软件中添加塔影效应[10],选择势流模型。
湍流风的风速和风向是时刻变化的,为控制偏航角的变化,本文研究偏航对风力机载荷的影响。采用稳态风进行仿真,并设垂直入流角为0°,定义风速与风轮轴向的顺时针方向夹角为偏航偏差角 α的正方向。
2 理论分析
在偏航状态下,叶片主要气动受力截面的受力状态如图3所示。

图3 偏航状态下翼型的入流状态Fig.3 Inflow of airfoil in yaw state
图 中:Vω为 叶 素 旋 转 线 速 度;V0,V1,V2为3个 方向 偏 离 风 速 主 方 向 角 度 为 δ0,δ1,δ2,且 大 小 相 同 的风速矢量,其对应的3个相对合速度为VS0,VS1,VS2;θ0,θ1,θ2均 为 叶 素 的 实 际 迎 角。
当叶片处于图1中的位置2和位置4时,偏航偏差角主要影响叶片径向入流角。径向入流角对翼型气动的影响是对称的,对风轮整体载荷平衡的影响相对较小,但叶片在这两个位置的载荷差异仍然受叶片仰角、锥角及预弯等因素的复合影响。当叶片处于图1中的位置1和位置3时,偏航偏差角主要影响叶片翼型的入流迎角及速度,叠加上风剪切形成的不同高度上风速的差异,叶片在这两个位置的载荷差异会更加明显。当偏航偏差角为正值时,位置1对应的叶素入流状态为图3中的V1风速矢量,位置3对应的叶素入流状态为图3中的V2风速矢量。当偏航偏差角为负值时,位置1对应的叶素入流状态为图3中的V2风速矢量,位置3对应的叶素入流状态为图3中的V1风速矢量。值得注意的是,以上4个位置为叶片入流分析的典型位置,其他相近位置也会有相似的表现,但入流状态和受力更加复杂。
由于δ角度并不大,所以近似认为速度矢量的法向分量V·cos δ=V不变,而合速度VS为

式中:V·sin δ为速度矢量的切向分量。
由 δ角度引起的VS0,VS1,VS2的差异不可忽略。叶素迎角θ为

式中:β为叶片叶素的位置角,数值上等于叶片桨距角与叶素扭角的叠加。
当Vω/V值较大时,由 δ引起的迎角变化很小,即 θ0,θ1,θ2差 异 并 不 大;但 当Vω/V值 较 小 时,由 δ引 起 的 迎 角 变 化 不 能 忽 略,即 θ0,θ1,θ2会 有明显差异。
叶素翼型迎角一般在非失速范围。从图3中可以分析出 δ引起的合速度VS和迎角 θ的变化是相反的。但VS和 θ两个变量与翼型的升阻力均是正相关的。所以当Vω/V值较大时,主要引起合速度值的变化,迎角变化可以忽略,能定性地影响升阻力变化;当Vω/V值较小时,合速度和迎角均发生变化,但不能确定对升阻力变化的影响。
Vω/V值与叶尖速比正相关,当风力机在额定风速以下正常运行时,叶片的叶尖速比一般大于8;在额定风速以上正常运行时,叶尖速比为4~8,风速越大,叶尖速比越小。由此可见,风力机运行在不同风速状态下的偏航对载荷的影响是不同的。
3 仿真结果及分析
变桨变速型风力机在额定风速之前处于转矩控制阶段,桨距角不变。在达到额定风速后转为通过控制桨距角进行恒功率控制。风力机运行在不同的控制阶段有不同的载荷表现。在小于额定风速的稳态风(V=6m/s)条件下,不同偏航偏差角度下的风力机的输出功率曲线如图4所示。
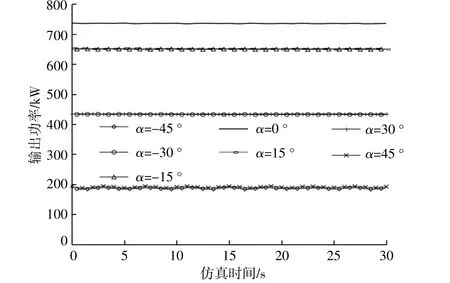
图4 风力机输出功率Fig.4 Output power of the wind turbine
由图4可知,当风速低于额定风速时,偏航偏差角的绝对值越大,风力机的输出功率越小,偏航偏差角的绝对值相同时输出功率基本一致。这是由于当风速低于额定风速时,风力机主要运行在最佳Cp条件下,偏航角的存在使风轮吸收的气动功率减小,输出功率对应下降。
轮毂中心My和Mz载荷是传导并影响机舱和塔架的主要载荷量。图5为6m/s风速下旋转坐标系下的My和Mz的载荷。

图5 旋转坐标系下的轮毂中心载荷Fig.5 Rotating hub load of the wind turbine
由图5可知:My和Mz载荷均表现出随偏航偏差角的变化而明显改变;各曲线的均值均在0kN·m附近,相比于0°偏航偏差角的载荷曲线,偏航偏差角正向越大,载荷曲线的波动幅值越大;偏航偏差角负向越大,载荷曲线波动幅值越小。由于旋转坐标系的坐标轴固定在轮毂上,在位置上随风轮旋转,所以My和Mz载荷曲线具有相似的形状,主要差异是周期变换的相位不同。
图6为6m/s风速下定坐标系下My和Mz载荷。由图6可知:当偏航偏差角为0°时,My在均值为-200kN·m的水平波动,其偏离0kN·m主要是叶片的锥角和叶片预弯及重力的共同作用导致的;当偏航偏差角小于0°时,My均值更接近0 kN·m,波动幅值也比0°偏航偏差角时小;Mz的均值和波动幅值均随偏航偏差角减小而变小;当偏航偏差角大于0°时,偏航偏差角越大,My均值的绝对值越大,波动幅值则无明显变化;而随着偏航偏差角变大,Mz的均值无明显变化,但波动幅值变大。

图6 定坐标系下的轮毂中心载荷Fig.6 Stationary hub load of the wind turbine
根据上述分析可知,在低于额定风速的转矩控制阶段,风力机的偏航偏差角对风力机轮毂中心载荷有显著影响,偏航偏差角的存在相应地降低了风力机的输出功率。但正向的偏航偏差角导致轮毂中心载荷增大,负向的偏航偏差角有一定的减小轮毂中心载荷的作用。
当风力机运行在额定风速以上时,可通过控制桨距角的变化限制转速和功率的变化。其载荷特征也与额定风速以下不同。在大于额定风速的稳态风(V=12m/s)条件下,不同偏航偏差角度下的风力机的输出功率曲线如图7所示。
由图7可知,仅在 α=±45°时,输出功率有所下降,在其它偏航偏差角度下,风力机的输出功率均为额定功率3.0MW。可见大风条件下桨距控制能一定程度上弥补偏航偏差角导致的功率下降。

图7 风力机输出功率Fig.7 Output power of the wind turbine
图8为12m/s风速下旋转坐标系下的My和Mz载荷曲线。由图8可知:当偏航偏差角为0°和±15°时,My和Mz的差异较小;当偏航偏差角为±30°和±45°时,Mz和My载 荷 均 随 偏 航 偏 差 角的绝对值变大而变大,表现为最值和波动幅值增大;相同绝对值的偏航偏差角条件下,Mz和My载荷最值和波动幅值基本一致。
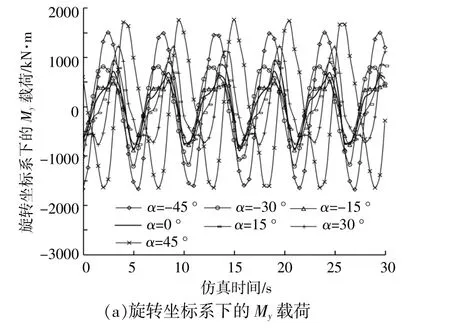
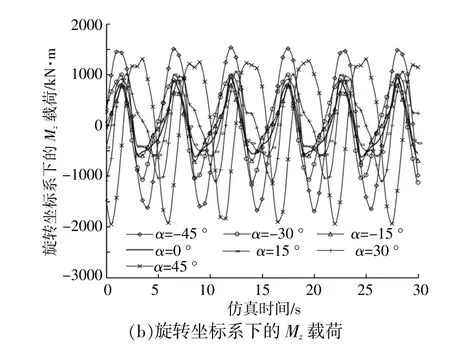
图8 旋转坐标系下的轮毂中心载荷Fig.8 Rotating hub load of the wind turbine
图9为12m/s风速下定坐标系下的My和Mz载荷曲线。由图9可知:当偏航偏差角为0°和±15°时,My载荷的差异较小,均值为450kN·m左右,其正向偏离0kN·m的原因是由于风剪切、风轮锥角和仰角的存在导致的风轮My固有的不平衡造成的;偏航偏差角的正向越大,My的均值负向越大,波动幅值越大;偏航偏差角的负向越大,My的均值正向越大,波动幅值越小;当偏航偏差角负向变大时,Mz的均值和波动幅值均在较低水平;当偏航偏差角正向变大时,Mz的均值和和波动幅值均明显增大。
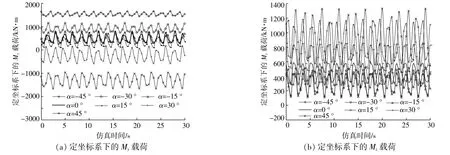
图9 定坐标系下的轮毂中心载荷Fig.9 Stationary hub load of the wind turbine
根据以上分析可知,在高于额定风速的变桨距控制阶段,在一定偏航偏差角范围内,风力机输出功率仍能保持恒定,但超过一定值后输出功率会明显下降。旋转坐标系下的My和Mz载荷均值均在0kN·m附近,波动幅值随偏航偏差角的绝对值增大而增大,并没有表现出偏航偏差角的正负引起的明显差异。但偏航角的正负会引起定坐标系下的My和Mz载荷的明显差异,正向的偏航偏差角会引起载荷更大的波动幅值,也会引起Mz更大的极限载荷。
4 结论
本文以某实验型3.0MW机组为研究对象,通过叶片气动分析和Bladed软件仿真方法研究了偏航偏差角对风力机输出功率及轮毂中心载荷的影响,得出以下结论。
①风力机运行在不同阶段的控制状态下载荷表现不同。在低于额定风速的转矩控制阶段,风力机的偏航偏差角对风力机轮毂中心载荷有显著影响,偏航偏差角的存在会相应地降低风力机的输出功率,但正向的偏航偏差角会导致轮毂中心载荷增大,而负向的偏航偏差角有一定的减小轮毂中心载荷的作用。
②在高于额定风速的变桨距控制阶段,在一定偏航偏差角范围内,风力机输出功率仍能保持恒定,但偏航偏差角超过一定值后,风力机输出功率会明显下降。旋转坐标系下的My和Mz载荷均值都在0kN·m附近,波动幅值随偏航偏差角的绝对值增大而增大,并没有表现出偏航偏差角的正负引起的明显差异。但偏航角的正负会引起轮毂定坐标系下的My及Mz载荷的明显差异,正向的偏航偏差角会引起载荷更大的波动幅值,也会引起Mz更大的极限载荷。
③不同的风速条件,偏航偏差角对风力机载荷的影响不同,相比于负向的偏航偏差角,正向的偏航偏差角会导致更大的风力机轮毂中心载荷。

