基于法向修正与位置滤波的散乱点云去噪算法*

戴士杰，东 强，季文彬，李 慨，任永潮，贾 瑞

(1.河北工业大学 机械工程学院，天津 300130; 2.河北省机器人感知与融合重点实验室，天津 300130)

0 引 言

随着计算机科学技术的迅速发展，物体表面的三维重构技术被广泛应用于计算机辅助设计(CAD)建模、逆向工程、计算机图形学以及计算机辅助工业设计等多个领域[1～3]。由于受测量设备自身缺陷和测量环境的影响使得测量得到的点云含有不同程度的噪声。因此，对三维散乱点云模型的去噪研究已成为数字化模型重构领域的热点问题之一[4]。

现有的采样模型去噪方法主要分为网格模型去噪和散乱点模型去噪。网格模型去噪需要先对采样点网格化，而散乱点模型去噪是针对获取的采样点利用其位置信息直接进行去噪处理，近年来逐步成为研究热点[5]。郭进等人[6]提出了采用密度K-means和改进双边滤波的点云自适应去噪算法，实现同时对大尺度和小尺度噪声的去噪处理。徐高鹏等人[7]在进行三维表面重建时利用Statistical Outlier Removal滤波器中的Kd-Tree算法进行去噪处理。林洪彬等人[8]提出了一种基于参数自适应各向异性高斯核的散乱点云保特征去噪，实现了散乱点云模型的各向异性保特征去噪。Fu Y等人[9]针对双边滤波算法不能同时对平坦区和尖锐区的噪声点进行光顺处理，通过改进K邻域的搜索方式，提出了保特征的点云去噪算法。Liang X H等人[10]在已有滤波技术的基础上，提出了基于自适应最优领域的散乱点云降噪算法，采用改进的三边滤波算法实现了法向矢量滤波和位置滤波。

散乱点模型去噪的基本原理是噪声点沿法向方向进行微小偏移，由于噪声的干扰使得采样点的法向估计存在较大误差，并且位置滤波时滤波因子不能随采样点局部几何特征自适应变化，使得去噪后的模型特征失真。针对上述两种问题，本文提出一种基于法向修正与位置滤波两步法的点云保特征去噪算法。首先对采样点的法向进行双边滤波修正；通过对滤波参数进行自适应取值设置，构建滤波参数自适应的高斯核函数；最后将修正后的法向与滤波参数自适应的高斯核函数相结合构建新的点云滤波模型。该算法在有效去除噪声的同时能较好保留模型的特征细节。

1 基于法向修正与位置滤波两步法的点云去噪算法

1.1 点云去噪原理

散乱点云去噪的基本原理是点沿着法向方向进行的微小偏移。如图1所示。

图1 去噪原理示意

图1中，Ω(p)为由采样点及其邻域点拟合的曲面，pi为初始噪声点的位置，ni为pi的法向，π为以ni为法向的切平面，p′i为沿法向偏移后的位置。

散乱点云滤波的数学模型为

pout=pi+ni·d

(1)

式中pout为滤波后的点云数据，d为采样点pi沿法向移动的距离，其具体表达式如下

(2)

ξij=Wc(‖pi-pij‖)Ws(‖〈pi-pij,ni〉‖)

(3)

(4)

Ws(‖〈pi-pij,ni〉‖)=

(5)

式中N(pi)为点pi的最近邻域,Wc为空间距离权重核函数;Ws为特征保持权重核函数。‖pi-pij‖为点pi与邻域点pij的欧氏距离，‖〈pi-pij,ni〉‖为采样点pi与邻域点pij的距离向量在该点法向上的投影。滤波参数σc和σs的取值决定着权重值的大小，σc越大，光滑效果越好；σs越大，特征保持效果越好，然而过大的σc值会产生过光顺，影响模型的特征保持效果。

上述去噪方法主要存在2种缺陷：1)由于噪声的干扰使得估计的采样点的法向量存有较大误差，去噪后易造成模型尖锐特征磨平失真，严重时会导致模型的缺损；2)滤波参数σc和σs的取值通常由用户自定义设置，在去噪过程中滤波参数固定且不能最优化选择，使得滤波权重不能自适应改变，导致模型的过光顺或去噪不完全。

因此，本文从法向修正和构建滤波参数自适应取值的高斯核函数2个方面对上述滤波模型进行改进，提出了基于法向修正与位置滤波的散乱点云去噪算法，实现了模型的保特征去噪，有效避免了模型特征细节失真。

1.2 点云的法向修正

高精准的法向量是点云位置滤波的重要条件，为了快速得到精准的点云法向，首先采用主成分分析法(PCA)[11,12]来粗估点云初始法向，作为点云修正的输入法向，其具体步骤如下：

假定P=(pi,i=1,2,3,…,n)为原始点云数据，pi∈R3，pi1,pi2,pi3,…,pik为采样点pi的最近K邻域，由PCA算法可知，pi的协方差矩阵C为

(6)

(7)

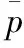
(8)

(9)

(10)

(11)

式中 参数σd和σn分别为距离偏差带宽和法向偏差带宽，在文献[11]中，参数σd和σn的取值为固定值，在平滑区域法向精度较高，而尖锐区域法向存在偏差。为了得到更精准的法向，根据采样点的局部几何特征自适应控制参数σd和σn的取值。利用采样点与邻域点的平均距离来控制距离偏差带宽σd，利用采样点法向与邻域点法向的标准偏差来控制法向偏差带宽σn。通过对参数自适应取值设置，不仅可以有效提高尖锐特征的法向精度，而且还对噪声起到了一定的光顺作用，参数σd和σn的具体表达式如下

(12)

(13)

(14)

(15)

1.3 点云的位置滤波

在进行散乱点云的位置滤波时，利用采样点与邻域点的平均距离来控制平滑因子σc，利用采样点与邻域点的距离偏差在采样点上投影的标准差来控制特征保持因子σs，通过对滤波参数自适应取值设置，构建了滤波参数自适应的高斯核函数，使得特征保持权重和光顺权重能随采样点的几何特征自适应改变，有效避免了低频区去噪不完全和高频尖锐区特征失真，保留了原始点云模型的特征细节。滤波参数σc和σs的具体形式为

(16)

(17)

(18)

(19)

将修正后的法向作为散乱点云的位置迭代方向，并结合滤波参数自适应的高斯核函数对式(1)进行改进，构建了新的点云滤波模型

(20)

(21)

(22)

(23)

(24)

本文所提基于法向修正与位置滤波两步法的点云去噪算法的基本步骤简述如下：

输入：含噪声的点云数据P。

步骤1 读取含噪声的点云数据P，设置领域点数k,法向滤波修正次数t和滤波次数γ的值。

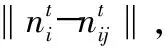
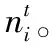
输出：去噪后的点云数据pout。

2 实验结果与分析

在VS2013编程环境下运用Pcl1.8.0进行算法的编写与测试。通过对3种不同的点云模型(Fandisk模型、Head模型、Hand模型)加入30 dB的高斯白噪声，然后利用不同的去噪算法进行对比实验。本文从法向修正精度和去噪精度2个方面对所提算法的有效性进行分析。

2.1 法向修正误差分析

本文首先利用所提法向滤波修正算法对带有30 dB高斯白噪声的Fandisk模型进行法向滤波修正实验，其修正结果如图2所示，图2(a)为滤波修正前的初始法向，图2(b)为利用本文算法迭代滤波5次后的法向修正结果。由图2(a)可知，由于噪声点的干扰，使得模型尖角和棱处的法向有较大偏差。若按此法向进行点云的位置滤波则会造成模型的边缘损坏。由图2(b)可知，经本文算法滤波修正后，模型的法向精度得到了提高，其尖角和棱上点的法向能与邻域点法向保持一致，可为点的偏移提供精准的法向。

图2 Fandisk模型法向量修正对比

对Fandisk模型进行多次迭代滤波，然后对修正后的法向误差进行分析，以无噪声模型的法向为参考法向，通过计算修正后的法向与参考法向的偏差，利用法向偏差均方根(root mean square，RMS)[11～14]定量分析本文算法的修正精度。其RMS值越小，修正后的法向精度越高。RMS的数学表达式如下

(25)

(26)

式中N为模型中点云个数；nref为参考法向，nest为滤波修正后的法向；τ为阈值，当修正后的法向与参考法向的点积大于阈值τ时，认为该法向与参考法向偏差90°。本文的τ值的选取与文献[11～14]相同，法向夹角阈值均取10°，即τ=0.984 8。图3为Fandisk模型经3种不同法向修正算法的法向偏差均方根的统计结果，由图3可以看出，3种方法的法向均方根误差均能达到收敛状态，而本文算法的收敛速度最快，并且达到收敛时误差最小，为0.624 rad。由此可以证明本文算法能较精准地估计点云的法向量。

图3 3种法向修正算法的法向偏差均方根

2.2 点云去噪结果分析

3种模型的去噪结果如图4～图6所示。对比图4(c)～(f)可以看出，本文算法能较好地保留Fandisk模型的棱角，能同时实现低频区平滑光顺和高频区保特征去噪；对比图5(c)～(f)可知，本文算法能很好地保留Head模型中眼部、嘴部等细节特征，未发生细节失真；对比图6(c)～(f)可以看出，本文算法能较好地保留着Hand模型的特征细节，去噪后模型更接近原始模型。本文算法由于对点云法向量进行了迭代滤波修正，使噪声点光顺迭代的方向更加精准，并且位置滤波时滤波参数可随采样点的几何特征自适应取值，使得高频尖锐区和低频平坦区能同时达到去噪的效果。

图4 Fandisk模型的去噪结果

图5 Head模型的去噪结果

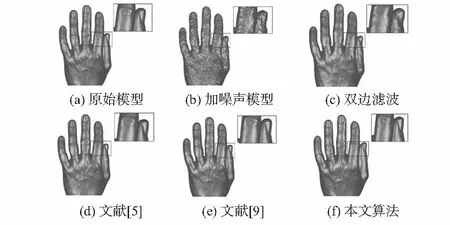
图6 Hand模型的去噪结果

在进行误差计算时，将原始点云模型作为参考，把去噪后点云模型中的各点与参考点云模型中的最近点的距离作为去噪误差。表1为对去噪后的平均误差、均方根误差和最大误差的统计结果，由表1可知，本文算法与其他去噪算法相比较，去噪后点云模型的3种误差均为最小，表明了本文算法能更好地保留原始模型的特征细节，去噪结果更接近理想模型。

表1 不同去噪算法的误差统计结果

2.3 参数的选取

本文算法中含有3个需要用户指定的参数：邻域点数k、法向修正迭代次数t和噪声点的迭代次数γ。邻域点数k的取值不当会严重影响去噪后模型的精度，过小的k值使得局部几何特征估计不准，过大的k值可能会将跨特征的领域点包含在内，去噪时会导致模型特征被磨平。本文算法经多次实验验证，当k=18时，模型的去噪效果最好；由图3中不同法向修正算法的误差分析可知，随着迭代次数的增加，法向偏差均方根先快速减小后达到收敛状态。本文算法的法向滤波修正迭代次数为5时，模型的法向误差达到收敛状态，故在本文中t=5；由图7可知，3种点云模型的均方根误差随着去噪迭代次数的增加呈现先减小后增大的趋势，当迭代次数为5时，各模型的均方根误差最小，最接近原始模型。故在本文中迭代次数γ=5。

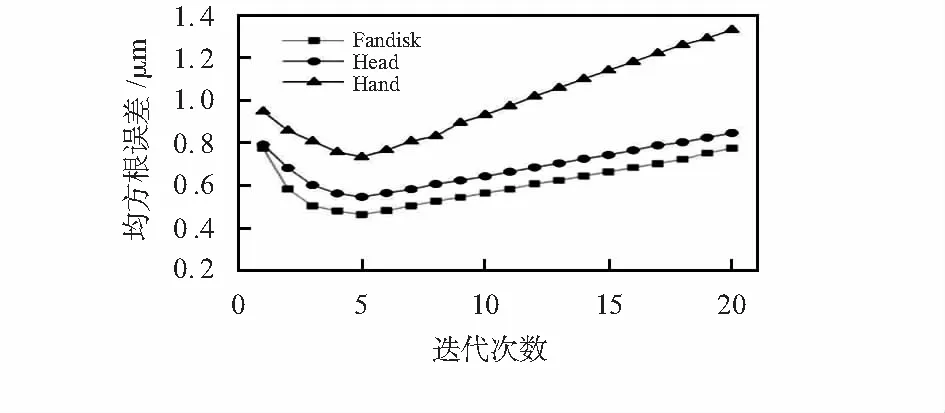
图7 不同模型的均方根误差

3 结 论

针对传统点云去噪算法易造成点云模型特征细节失真的问题，提出了一种基于法向修正与位置滤波的散乱点云去噪算法。该算法能够对邻域点法向进行双边加权，利用邻域法向加权之和更新采样点的法向，提高了模型尖锐特征处的法向精度，为散乱点云模型的位置滤波提供了精准的法向。构建了能随采样点局部几何特征自适应取值的滤波参数，使得位置滤波时模型的特征保持权重和光顺权重均能自适应改变。将修正后的法向和滤波参数自适应的高斯核函数相结合构建了新的点云滤波模型，实现了点云的各向异性保特征去噪。