基于BP神经网络的LT模型影响力最大化研究

张凯伦 ZHANG Kai-lun；汪超 WANG Chao；王璐 WANG Lu

（①安徽工业大学，马鞍山 243002；②安徽工程大学，芜湖 241000）

0 引言

随着互联网的高速发展，越来越多的人习惯在线上社交平台获取信息，社交网络中的影响力最大化问题（IMP）成为热点研究问题。影响力最大化问题，一般是指在网络中筛选出k个具有强大影响力的用户，通过给定的离散信息传播模型将信息传播至最大范围。Domingos和Richard[1]最早将IM问题数学化，随后，Kempe等[2]在此基础上，首次提出可以用离散优化的方式解决IM问题，并证明了影响力最大化问题的性质是NP难的。文献也分析了两种应用广泛的信息传播模型，分别是独立级联模型（IC model）和线性阈值模型（LT model）。IC模型由于传播概率的随机性，不稳定性偏高，而LT模型属于一种价值累计模型，能够刻画个体与个体、个体与集体之间相互影响的情形，可以避免这种情况。

在Kempe等[2]提出贪婪算法后，研究学者在贪婪算法的基础上提出了众多解决IM问题的方法。传统优化算法包括模拟退火算法[3]，禁忌搜索算法[4]等，然而传统算法总是需要遍历网络中所有节点，对于规模稍大的网络不具有适用性。为了提高计算精度和效率，一些智能优化算法被相继提出，例如常用的粒子群优化算法[5]，人工蜂群优化算法[6]等。近几年，Mirjalili等[7]提出的樽海鞘优化算法（SSA）也被应用于各种优化问题。在如今的信息化时代，复杂网络数据骤增，仅依赖智能优化算法不再能妥善处理该问题。为了尽可能多地扩散影响，数据驱动方法被应用[8]。由于数据驱动技术善于发现数据中的复杂关系，促使模型适应数据，并能够根据不同的数据而改变，在各研究领域得到广泛应用。另外，由于BP神经网络具有结构简单、易训练且预测效果良好等优点[9]，因此，本文选择经典的BP神经网络来优化预测模型。

本文结合数据驱动方法构建了基于BP神经网络的影响力最大化算法求解模式，首先以网络结构特性作为选择样本节点的标准，挖掘出具有样本代表性的部分节点，构造数据样本，用于训练模型，然后在改进的SSA算法框架下进行计算。

1 相关知识

1.1 影响力最大化问题

影响力最大化一般被定义为：给定一个图G=（V，E）及其上的一个离散时间递进性传播模型，即线性阈值模型，其中V定义为网络中所有节点的集合，E表示任意节点之间的邻边。给定一个预算k，要找到一个最多k个点的种子集合S0*，使得该种子集合的影响力扩展度达到最大。其数学公式如下：

LT模型作为一种价值累计模型，首先给网络G中每个节点分配一个阈值θv（θv≤1），节点之间的边权重由节点入度Lin(v)决定，边权重计算方式为。若活跃节点u对邻居节点v的影响力满足，则称节点u成功激活了节点v，反之激活失败。

1.2 目标函数

本文基于LT传播模型定义了目标函数：

式中，σ（S0）记录了种子集在传播中激活的所有节点，m是平衡参数。

1.3 BP神经网络

BP神经网络作为一种被广泛应用的多层前馈式神经网络，又被称为误差逆传播算法，基本模型由输入层、隐藏层和输出层组成。传播方式分为以下两个阶段：

式中，f为激活函数，w代表节点之间的权值，b代表节点阈值。tansig函数表达式为：

反向传播子过程如下式所示：

式中，E（w，b）为误差函数。

2 算法框架

2.1 优化算法

2017年，Seyedali Mirjalili等[7]提出了一种模拟樽海鞘生物的链式群行为的新型群智能优化方法（salp swarm algorithm，SSA）。在链式群中分为领导者和追随者两部分，领导者负责指挥追随者前往食物存在的方向。由于结构的特殊性，追随者只受前一个樽海鞘的影响，这使SSA算法具有很强的全局探索能力。

salps初始化信息为：

式中，D为空间维数，N为种群数量，搜索空间的上界为ub，下界为l b。

领导者初始化的方式为：

跟随者更新的方式为：

式中，Fj表示食物在第j维空间中的位置，l为当前迭代次数，L为最大迭代次数。其中sa l pij（l）为在l次迭代时，第i只salp在第j维空间中的坐标。c2和c3为区间[0，1]内的随机数，c2决定移动长度，c3决定移动方向。c1用于控制整个群体的探索和开发能力，表达式如下：

2.2 种子集更新

由于SSA算法不适用于离散型优化问题，本文使用Sigmoid函数对算法中的变量进行离散化。为了避免让算法在搜索过程中陷入局部最优，本文利用交叉变异操作来增强种群多样性。首先，从结构中心性指标排名前百分之30的节点中产生初代种子集。在产生第一个种子集后，本章节使用交叉变异[10]来确定新的种子集成员，并将SSA算法中的位置更新公式作为确定个体选择交叉位置的依据。

Sigmoid函数公式如下所示：

种子交叉位置由下式确定：

式中，Si表示经过映射之后的樽海鞘位置向量。系数w1，w2无固定数值，文中假设给定系数分别为1.4和0.8。

在交叉过程中，确定当前最优的一组个体和第二组个体中的交叉位置，将两组个体相应位置的索引进行互换，形成两组新的个体。小范围变异行为如下：若rand<0.1，则种子集将再次进行更新，然后进行新一轮的迭代计算。

3 算法仿真

3.1 数据集

为了验证该算法的有效性，本文构造了一个规模为500节点的BA网络，节点度分布与基本信息如图1和表1所示。

图1 BA网络的节点度分布

表1 BA网络数据的基本信息

3.2 实验设置与结果分析

本文首先以度中心性、介数中心性和Pagerank等网络结构特性作为选择样本节点的标准，挖掘出前百分之30具有样本代表性的节点，形成产生初始种群的节点候选池，每次从中挑选百分之20的节点，构造10000组数据样本。其次，在BP训练数据阶段，设置三层神经网络，隐藏层神经元个数设为10，两级网络的权重均设为（-1，1）之间的随机数。以节点特征作为输入变量，以节点影响力作为输出变量，其中9000组样本用于训练，1000组样本用于预测。步长设为10，迭代次数设为50000。在得到良好的预测效果后保存训练网络，利用增加了交叉变异操作的SSA算法进行计算。图2为BP神经网络对数据样本的训练效果，可以看到，训练精度达到百分之93。

图2 BP神经网络的训练精度

另外，本文罗列了几种经典的结构中心性算法与本文算法进行对比，分别是BC[2]、DC[11]、CC[11]以及Pagerank算法[12]。表2记录了几种不同的优化算法得到的种子节点影响力，可以看出，本文算法的影响力结果略高于其余算法。图3显示，本文算法获取的节点传播能力高于其余几种算法，并在计算迭代18次时呈现上升趋势。因此，在其他条件保持一致的情况下，能够看出本文算法挖掘出的节点传播性能更强。

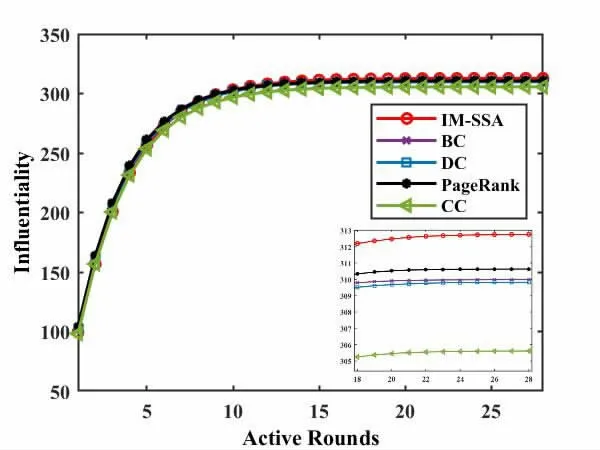
图3 IM-SSA与其他算法的传播对比

表2 IM-SSA算法与几种结构中心性算法的效果对比

4 结语

随着大数据时代的发展，数据驱动被用于各种优化问题，显示了数据驱动优化方法的优越性，因此，本文基于数据驱动思想建立代理模型，提出了一种BP神经网络下的影响力传播最大化算法。该算法基于网络结构特性生成样本数据，利用BP神经网络训练样本数据，优化预测模型，最后利用SSA算法进一步优化，并在SSA算法框架中使用交叉变异以增强样本多样性。相比于几种经典的结构中心性算法，本文算法获取了传播性能更好的节点。在以后的优化问题研究中，数据驱动或许能够发挥更重要的作用。