航空发动机燃烧室出口温度场数值模拟研究

郭青青 GUO Qing-qing；李柳 LI Liu

（①三亚航空旅游职业学院，三亚 572000；②中国航发沈阳黎明航空发动机有限责任公司，沈阳 110043）

0 引言

航天航空的发展对于飞机的运行提出了更高的要求，具体而言，要求其发动机应当有着更低的运营成本，更低的污染排放以及更高的运行可靠性。其中，对于运营成本的影响，航空发动机的涡轮叶片和导向装置的使用寿命是关键的两个因素[1]。而燃烧室出口位置的温度则对这两个结构装置的使用寿命有着极大的影响，进而影响到发动机的整体运营成本[2]。从这一方面可以看出，对于发动机燃烧室出口位置温度分布情况的研究，以及对其进行的相关计算和仿真，都有着十分重要的现实意义。尽管航空发动机燃烧室出口位置的温度分布情况测试能够完全通过计算取代，但通过计算得出的数据可以大大降低试验的工作难度以及工作量。另一方面，由于航空发动机燃烧室中各个部件的设计逐渐向着高温、升温热熔的方向发展，因此燃烧室出口的温度也在持续不断地提升。在出口位置温度场的不稳定以及分布不均匀等问题，都会造成燃烧室中各个部件热力状态向着不良趋势发展，进而使整个航空发动机出现不稳定和各项性能指标降低的问题[3]。基于此，为提高航空发动机运行稳定性，实现航空航天的可持续发展，本文下述将结合数值模拟，对其燃烧室出口位置的温度场进行深入研究。

1 航空发动机燃烧室出口温度场数值模拟

1.1 航空发动机燃烧室性能分析

由于航空发动机燃烧室的结构较为复杂，为了能够确保后续对温度场数值模拟的精度更高，在模拟前对燃烧室性能进行分析，并实现对燃烧室结构的简化。图1为燃烧室中主要的火焰筒结构简图。

图1燃烧室火焰筒结构简图

图1 中，A表示二排掺混孔；B表示一排掺混孔；C表示旋流器。结合该结构特点，对燃烧室的性能进行分析。在该燃烧室火焰筒中包括15个头部，每一个头部上各有一个旋流装置。在明确关键结构的基本组成后，为实现对燃烧室性能的分析，对燃烧室进行建模。在建模时，对头部形状予以细化处理。根据航空发动机的基本参数，结合图1中的结构，设定燃烧室的总体尺寸，如图2所示。

图2中对应主燃孔的截面为110mm，对应掺混孔的截面为130mm。火焰筒是由大量的不规则曲面和曲线切割而成，这样就可以最大限度地贴近真实的燃烧室。在冷却孔的设计中，考虑到冷却孔对整体流场的影响不大，采用环形带代替冷却孔，以满足冷却气流的流速要求。从计算复杂度和相似度两方面出发，对全燃烧室进行模拟。

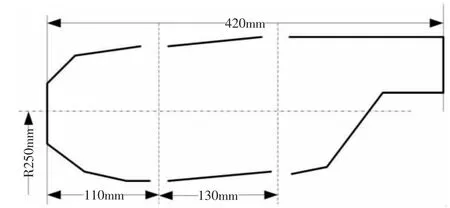
图2 燃烧室轴向截面及对应尺寸图

在燃烧室当中，流动形式均遵循质量守恒定律，即，在每一段时间内，液体微元体内的质量的增长，等于在相同的时间间隔内，进入这个微元体内的净重。从这个规律出发，可以得出一个燃烧室内流体的质量守恒的公式：

公式中，ρ表示流体密度；m表示时间；V表示速度。在此基础上，对燃烧室的性能进行分析得出：燃烧室内旋流器的下游回流区域主要受到头部结构的影响：回流段的回缩会使回流段的长度变短，回流区域变窄，回流速率变慢；旋流器在旋流较大时，会形成较强的旋流，形成小范围的回流带；旋流数较少的旋流器，其下游出现弱旋流，出现大范围的回流。通过缩短回流段长度和降低回流速率，可以有效地减少高温气体在燃烧室中的停留时间，从而实现对废气的控制。此外，喷嘴的形状还影响到喷嘴的温度分布：喷嘴的回缩可以减少局部的高温区域，提高出口的温度对称；两种旋流数目不同的旋转器列阵，使局部温度范围增大。

1.2 温度场数学建模

采用有限元方法建立燃烧室的温度场模型。用曲线拟合得到了温度场中各个物理性质的变化规律，并以此建立温度场数学模型。通过有限元法，将微分方程转变为代数方程，实现离散化处理，这一过程的原理如图3所示。

图3 有限元离散化处理原理图

根据几何对称性，基于三维结构，数学模型主题为描述控制体内三维变物性稳态热传导方程：

公式中，x表示空间单元节点横坐标；y表示空间单元节点纵坐标；z表示空间单元节点空间坐标。再将面温度场数据作为基础，构建更高精度的燃烧室温度场模型。

1.3 fluent软件的温度场数值模拟

fluent软件可以实现对燃烧室模拟区域内流畅细节的细致刻画，应用该软件实现对燃烧室温度场数值模拟能够达到更高精度效果。在运行fluent软件后，选择Fluent version选择界面，选择默认2ddp。然后打开网格文件，在菜单中按“文件→读取→Case→fin”的顺序进行操作。结合上述航空发动机燃烧室结构，为Gambit创建一个地区时，指定一个没有大小单元的计算区域，此时点击确定后，可以扩大或缩小面积。在Grid菜单中选取Scale对话方块。本文研究问题是一个稳定问题，在Solver中已被默认，只需要对温度场进行求解。通过菜单DefineModels→Models→Energy，完成对模型选择，并设置边界条件，进行对温度场的设置模拟。

1.4 最小二乘方法的温度场重建

在利用fluent软件实现对温度场数值的模拟后，结合最小二乘法，对燃烧室温度场进行重建。在温度场当中，声波沿着任意一条声波路径的飞行时间可以用下述公式形式表示：

公式中，tFLY表示声波在温度场中的飞行时间；a表示空间状态因子；s表示距离。其中，a的取值为声波速度的倒数。图4为温度场内声波的飞行路径。

图4 温度场内声波的飞行路径示意图

按照图4所示，在温度场内划分8个区域，按照逆时针的方向依次用数字1~8进行标记。在每一个区域当中，温度都是未知的，但假设温度都是均匀分布的。为了再现燃烧室的温度场，必须通过计算得到各小区的温度。在上述公式基础上，计算得出某一路径k上，通过第i个小区域时消耗的时间：

公式中，tFLYki表示在第k条路径上，通过第i个小区域的飞行时间；Ski表示在第k条路径上在第i个区域当中的长度。再结合最小二乘法，得出下述关系：

公式中，A表示空间状态因子矩阵；t表示每个小区域的平均温度；S表示路径长度。通过计算得出小区域的平均温度，并按照这一流程实现对图4中8个小区域温度的计算。再进行80×80的双三次插值，利用该方法可以获得全燃烧室温度场的分布，从而可以重构出整个燃烧室的温度场。

2 实验验证

2.1 温度场模拟效果图

根据上述论述，实现对数值模仿方法基本应用思路的设计，为验证新的数值模拟方法的实际应用效果，进行下述实验验证。在严格按照上述操作完成对温度场的数值模拟后，得到如图5所示的温度场模拟效果图。

图5 温度场模拟效果图

以某发动机主燃烧室全环试验件出口温度场为实例，采用一根5点梳状总温热电偶周向转动的方法，摇摆机构每3°停顿3s，获得1次温度场数据，总共抖动120次，采集5min左右的温度场。在完成了对温度场数据的采集后，通过测试软件向可视化软件传输温度场数据，实现了对温度场的实时监测。从图中可以看出，通过上述数值模拟方式得到的温度场模拟效果图可以更全面、更直观地反映出温度场的特点。通过鼠标的运动，可以获得温度场的任何位置、径向和圆周方向的分布，从而快速地识别出温度场的质量。温度场模拟效果的质量取决于温度点的多少。如果温度点数太低，就会忽略热区，而不能准确地反映出温度场的真伪。由于主燃烧室的结构和实验费用等原因，测试的温点也不可能无限，因此必须根据以前的实验经验，选择合适的温度点。在此基础上，增加温度点的措施为：提高电偶表面温度传感器的测量点数；减少摆动间隔角度，获得更多的位置测量值。

2.2 温度场模拟精度

为实现对上述数值模拟结果精度是否符合规定要求的验证，在燃烧室中随机位置上设置5个测点，并对其进行现场测定。再从模拟结果中找到5个测点对应的位置，并获取该点在温度场模拟结果中的温度，将记录数据绘制成表1。

表1 温度场模拟精度验证结果表

对比各个测点的实际温度和模拟结果得出，二者相差不超过±0.3°C。通过对航空发动机燃烧室出口温度场数值模拟需求分析得出，模拟结果的误差不超过±1°C的范围，产生的误差都不会对最终结果造成影响。从表1中的数据可以看出，本文设计的数值模拟方法充分符合这一精度要求。因此，通过实验验证，该数值模拟方法具备极高的模拟精度，在实际应用中可以为温度场变化研究提供更加可靠的数据依据。从上述得出的实验结果可以看出，本文设计的数值模拟方法得到的结果仍然存在一定误差，为了进一步缩小误差，提高数值模拟精度，可以根据实际运算条件，在温度场数学建模操作中设置更多的节点和单元，并实现对燃烧室出口温度场细节的进一步刻画。温度点的误差与摆动装置的角度误差以及模拟软件本身的误差有着一定关联。因此，根据实际情况，尽可能选择具备更高精度的传感器、测量仪器等，并在利用软件进行数值模拟时做好滤波处理措施，以此减少外界环境干扰因素对最终数值模拟结果造成的影响。此外，温度测量设备是以电动方式实现功率传输，其动力传输是由多个齿轮构成的齿轮驱动。由于齿轮的间隙存在一定的传动空程，所以在采集温度场数据时，需要排除因空程角引起的测量角误差。

2.3 时间成本

在实现对数值模拟方法模拟精度的验证后，再从时间成本方面对该数值模拟方法的应用性能进行研究。仍然以上述航空发动机燃烧室温度场为数值模拟对象，对模拟过程中的计算时间进行记录。将温度场按照图4所示划分为8个区域，分别为①~⑧，将每一个小区域内得到数值模拟结果的时间只作为计算时间，将相关数据记录如表2所示。

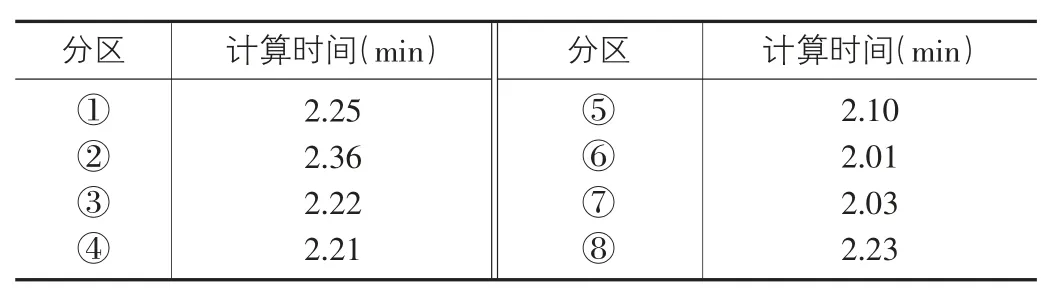
表2 数值模拟时间成本记录表

从表2数据可以看出，每个区域的数值模拟计算时间均在2~2.5min范围内，按照每个区域依次进行数值模拟生成结果，总时间成本不超过18min，而采用这种数值模拟方法可以实现对多个分区的同步模拟，因此最终时间成本远小于18min，证明本文设计的数值模拟方法消耗时间成本少，具备极高的模拟效率。

3 结论

通过本文上述论述，针对航空发动机燃烧室出口温度场进行了数值模拟研究。通过数值模拟，发现主燃烧区是燃烧区，主燃孔有一定的阻燃性，低主燃区出口及均匀温度场的加入孔起、落。同时，通过实验也实现了本文所述数值模拟方法的可行性验证，模拟结果的精度得到有效提升，且模拟效率快，为后续对燃烧室出口温度场研究，节省更多时间成本，具备极高的应用价值。同时，根据数值模拟结果也能够为航空发动机的性能优化提供依据，促进航空航天事业发展。