基于AHP-SPA的仓储智能化改造项目施工阶段风险评价

沈丹华 SHEN Dan-hua；林婷婷 LIN Ting-ting

（①新疆大学商学院，乌鲁木齐 830000；②广州大学机械与电气工程学院，广州 510006）

0 引言

近年来，随着“中国制造2025”战略的实施和推进以及智能制造技术的研究和应用，在智能制造领域不断涌现的新技术、新理念、新模式推动着智能仓储的建设。仓库是物流服务链上各环节的重要节点[1]，智能仓库运用高度自动化设备和管理模式，构成仓库的设备控制系统以及结构复杂[2]。依托现代信息技术形成的智能仓库在现代物流管理中发挥着仓储、保管、配送、加工、调运、信息传送等开发功能[3-4]，并且智能仓储具有自动化、智能化的特点，可促进仓储管理效率及企业经济效益的提升[5]。然而，在仓储智能化改造的施工阶段，软件和硬件技术相对复杂，与其他建设项目相比仓储在智能化升级过程中的风险具有更高的不确定性。因此，对仓储智能化改造项目施工阶段风险进行科学有效的评价成为仓储智能化改造项目风险管理研究亟待关注的方向之一。

对仓储智能化改造项目施工阶段指标体系进行赋权和评价是进行风险评估的核心，由于评价系统内部的复杂性与系统外部的多变性，影响风险评估指标信息的不确定。用传统的模糊综合评价法对具有复杂性和多变性的指标体系进行量化，同一层次的风险因素指标存在较大的差异。集对分析（SPA）法[6-9]可以从系统的角度来认识分析确定性和不确定性的关系，该方法是由赵克勤于1989年提出，其核心思想是确定与不确定的问题视为一个确定-不确定系统。该系统中，确定和不确定性存在相互对立、影响、联系的关系，并且在一定条件下可以相互转化。从同、反、异三个方面来描述事物之间的相互关系，并通过联系度来表达不确定性，从而把定性描述的不确定性转化为数值定量表述出来。使用的公式为：μ=a+bi+cj，其中a和b分别表示为两集合在同一问题下的“同一度”、“差异度”、“对立度”，规定a，b，c∈[0，1]，且满足归一化条件a+b+c=1；i为差异度系数，在[-1，1]区间视不同情况取值；j为对立度系数，规定其恒取值-1。公式μ=a+bi+cj计算的是三元联系数，随着系数的增加，不确定性逐渐弱化，计算分析结果会更加准确。层次分析法（AHP）是利用定量与定性方法相结合，进行多目标决策分析的方法，具有很强的实用性，能够对一些复杂和模糊的问题作出决策[10-12]。

为了更加合理客观地进行风险评价，本文采用基于层次分析法的集对分析理论（AHP-SPA）来对仓储智能化改造项目实施过程中的风险因素进行赋权，对评价信息的整体和局部分析辩证分析及数学处理，进而全面且系统的评价。

1 仓储智能化改造项目风险模型构建

1.1 建立指标体系

构建指标管理体系需要充分考虑仓储智能化改造项目系统的内部要素，确保指标能从不同方面反应出仓储智能化改造项目实施中的风险问题的实际情况，在最大程度上体现出风险评价的作用。

本文从经济风险因素、技术风险因素、组织风险因素、环境风险因素以及项目利益攸关方风险因素五个方面，以此构建了5个一级风险因素指标，20个二级风险因素指标，构建出仓储智能化改造项目施工风险评价指标体系，如图1所示。

图1 仓储智能化改造项目施工阶段风险评价指标体系

1.2 构建判断矩阵

在仓储智能化改造项目风险评价指标体系中，每个指标的重要性各不相同，确定各指标权重的合理性是依据评价结果做出正确决策的基础。判断矩阵各层级的指标因素的重要性程度赋值是由在仓储智能化改造项目实施过程中有丰富经验的5位专家，根据各指标因素发生时对项目的影响程度按1-9进行赋值。

式中Bxy为Bx相对于By的重要性，其中Bxy＞0且Bxy=Byx-1。B层以经济风险因素B1为例，B1＝{C1，C2，C3}为仓储智能化改造项目风险评价层次模型中B1对应的3级指标的集合，构造判断矩阵为：

式中Cxy为Cx相对于Cy的重要性，其中Cxy＞0且Cxy=Cyx-1

使用和值法计算判断矩阵中各风险因素的权重，首先按列向量归一化

式中αxy为判断矩阵中x行y列的数值，Wxy为αxy的归一化数值，m为矩阵的阶数。

各指标因素按行求和并归一化

式中Wx为每行判断矩阵之和；为每行判断矩阵平均值；AW为判断矩阵中各指标因素对应的权重值。

1.3 构建AHP-SPA评价模型

AHP-SPA权重计算方法是利用层次分析法构造判断矩阵并进行一致性检验，再通过集对分析理论中的同异反模型将专家组意见看作是不同的集对进行处理并归一化，最终得到权重。根据仓储智能化改造项目实施过程中的实际情况建立风险评估指标，将风险等级分为“低风险”、“中风险”、“高风险”，运用层次分析（AHP）与集对分析（SPA）耦合进行仓储改造在风险管理效果方面的动态评估。

集对分析理论是通过联系度来评估一个或多个事件的确定性和不确定性的理论方法之一，它假设两个属性可以在特定条件下相互转换[13-14]。集对分析算法运用联系度对不确定性进行描述，将不确定性的辩证认识转换为直观的数学模型，用来分析解决不确定问题。集对分析是由两个集合组成的集合体[15]，以Q（X，Y）为例，即集合X和集合Y，组成集合对Q=（X，Y）。X、Y集合之间可以用同一度、差异度、对立度来进行表述，即当评价指标处于一个确定的等级范围内时认定为同一，当评价指标在相邻等级范围内时可认为存在差异，当评价指标处于相隔的等级范围内时即可认定为对立。

在特定问题的前提下，分析了集合对的N个特征：S为Q集对中X、Y集合共有特性的个数；P为Q集对中X、Y集合相对立特性的个数；其余的特性F=N－S－P，其既不对立，又不为X、Y集合所共同具有[16]，其联系度μ表达式为

式中，i为差异度系数，i∈[-1，1]；j为对立性系数，一般情况下设定j=-1。

S/N代表X、Y两个集合的同一度，表示为a；P/N代表X、Y两个集合的对立度，表示为b；F/N代表X、Y两个集合的差异度，表示为c。

在考虑共有特性、对立特性、差异特性权重的联系度的情况下，其计算公式为:

特征元素的权重为：

由此可以将（2）式改写为：

2 实例应用

以某仓储智能化改造项目为例，建立风险评价指标体系（见图1），采用AHP-SPA风险评价模型进行风险评价。

2.1 仓储智能化改造项目专家评价

对各级指标因素层的判断因子，通过专家调查表，将各专家的权重相加，计算各层次指标因子的平均值，并进行两两比较得到各层级因子的判断矩阵，经过计算最终确定仓储智能化改造项目施工阶段风险评价指标权重表，如表1所示。

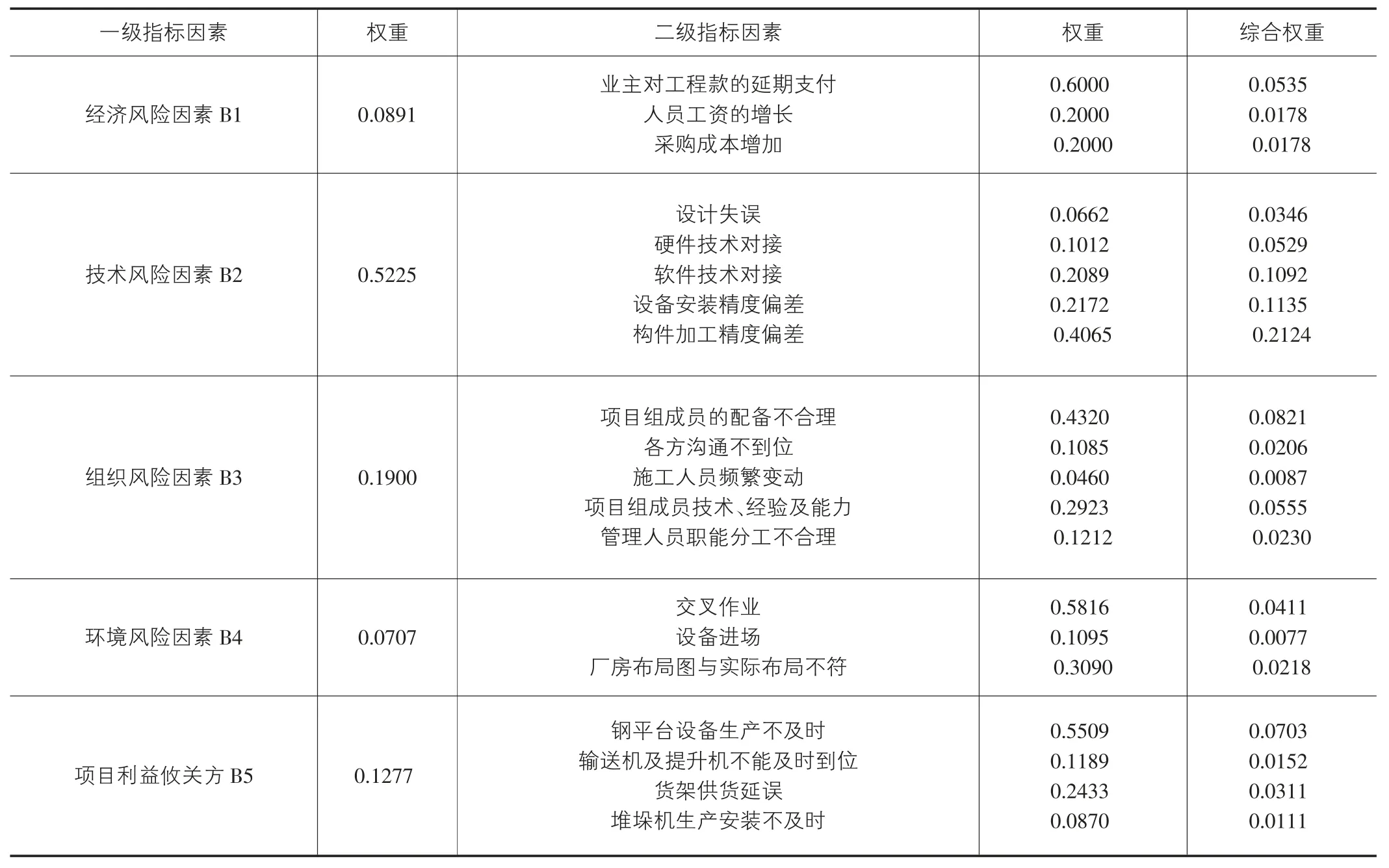
表1 某仓储智能化改造项目施工阶段风险评价指标权重

5位专家Ki（i=a，b，c，d，e）根据仓储智能化改造项目施工风险评价指标体系（图1），对该项目涉及的20个因素指标进行评价打分，打分结果按L代表“低风险”，M代表“中风险”，H代表“高风险”等级设定（见表2）。

表2 某仓储智能化改造项目施工阶段风险评价指标专家评分结果

2.2 指标因素联系度计算

根据5位专家K（ii=a，b，c，d，e）的知识背景，设各位专家权重为W1=（0.25，0.15，0.25，0.20，0.15），结合表1得到的综合权重，利用（3）式根据表2中各二级指标因素评分结果的占比情况，计算得到各专家评定的风险等级对应的联系度，见表3。为了减小层次分析法确定权重的主观性的影响，此次风险联系度计算分别对不考虑权重与考虑权重两种情况进行分析。

2.3 仓储智能化改造项目风险评价结果

①不考虑评价因素指标权重。

结合表3专家评定风险等级联系度，不考虑评价指标权重时，得出某仓储智能化改造项目施工阶段风险等级的平均联系度为：

表3 专家评定风险等级联系度

②考虑评价因素指标权重。

结合表3专家评定风险等级联系度，当考虑评价指标权重时，得出某仓储智能化改造项目施工阶段风险等级的平均联系度为：

③评价结果。

根据式（7），按照均分原则，把联系度的数值范围[-1，1]按3个 不 同 区 间 均 分 为X=[-1，-0.3333]、Y=[-0.3333，0.3333]、Z=[0.3333，1]，X、Y、Z分别代表某仓储智能化改造项目施工阶段风险程度，“高风险”“中风险”，“低风险”。由此得出：

1）在不考虑指标权重的情况下，在仓储智能化改造项目施工阶段，项目管理者需要加强风险管理，合理配置项目管理者配置、提高项目经理的风险管理意识，加强风险经理自身素质，把“中风险”等级因素指标提升为“低风险”指标因素等级。根据式（11），当i=1，j=-1时μ1=0.63，该系统处于“低风险”等级；相反，如果管理人员在风险管理过程中不能严格控制质量，减少风险因素的发生，则该体系称为“低风险”。标准因子将被降低，即当i=-1，j=-1时，得到μ2=0.01，该系统处于“中风险”等级。

2）在考虑指标权重的情况下，在项目实施过程中，项目管理人员应加强对项目的风险管理，进一步提高自身的风险意识和技术能力，根据式（12），即当i=1，j=-1时μ1=0.3415，该系统处于“低风险”等级；相反，当i=-1，j=-1时μ2=-0.2037，该系统处于“中风险”等级。

3 结论

通过对某仓储智能化改造项目施工阶段风险因素的调查与分析，从经济风险因素、技术风险因素、组织风险因素、环境风险因素、项目利益攸关方风险因素5个方面总结了业主对工程款的延期支付、人员工资的增长、采购成本增加等20个评价因素指标；建立了科学的AHP评价指标体系，根据集对分析理论，建立指标体系风险评价模型，并进行风险评价，确定风险等级。采用是否考虑权重情况进行分析，并且利用层次分析法确定指标因素权重，降低了只用专家打分来确定风险等级的主观性，使评价结果更加客观，为仓储智能化改造项目施工阶段的风险评价提供了新思路。