基于类龙伯格预测器的财务困境预警研究

任嘉嵩 伍胡星宇 任炜杰

【摘 要】 预测财务困境一直是财务管理中的重要环节，而传统基于卡尔曼滤波的动态预警算法在应对噪声分布不确定问题时难以保证预测结果的准确率，一定程度上降低了该方法的实际价值。针对其缺陷，文章创新性地提出了基于龙伯格观测器理论和线性矩阵不等式技术的预测算法，在噪声分布情况不能有效辨识或辨识误差较大时预测效果更优，同时简化了预测步骤，降低了计算复杂度。文章以沪深两市电力企业为例，结合龙伯格观测器理论设计预警模型，用线性矩阵不等式计算增益，应用数据分析和参数估计对各家电力企业财务状态进行跟踪和预测。同时与传统基于卡尔曼滤波的算法横向对比，更有力地突出类龙柏格预测器的预警效果和实用价值。

【关键词】 财务困境； 类龙伯格预测器； 线性矩阵不等式； 状态空间方程

【中图分类号】 F224.9  【文献标识码】 A  【文章编号】 1004-5937（2023）05-0038-08

一、引言

财务困境理论是公司管理中一个重要的研究领域[1]。当出现内部管理不善、行业局势动荡、产品竞争力不足等情况，可能导致公司财务状态由健康转入困境甚至导致破产。不过公司陷入财务困境是一个动态的、连续的、可预测的变化过程[2]。20世纪60年代以来，西方学者对财务困境预警展开了广泛的研究。从线性概率[3]、多元判别分析[4]、逻辑回归[5]等静态预警模型，到人工神经网络[6]、卡尔曼滤波[7]等动态预警模型，相关研究成果层见叠出。静态预测多基于发生财务困境前的单一时间样本数据，其优点是不需要考虑资金时间价值，计算简便；缺点则是忽视了不同时间点之间的有机联系。因为企业从健康转入财务困境是一个累积变异特性的过程，财务状态所表现的突变性往往是这种累积变异特性达到临界值造成的。因此，在对财务困境设计动态预警模型时应具备两个条件：第一，所选财务指标数据应该追溯数期，可反映财务陷入困境前较长时间的财务变动；第二，预警系统的设计应充分考虑到财务状态的累积变异特性。

在动态预警模型中，卡尔曼滤波作为当前较为主流的预测方法得到了广大学者的青睐[7-15]。孙晓琳等[8]将广泛应用于惯性导航、定位系统等领域的卡尔曼滤波引入财务系统，研究结果表明对？觹ST公司的财务预测拥有较高的辨识能力和跟踪精度。庄倩[9]在前人的基础上对财务预警模型做出改进，设计了超前n步预测。卡尔曼滤波通过输入输出观测数据，以实时递推的方式不断修正系统状态变量估计，且无需存储大量数据，通过观测新数据即可得到新滤波值，但在设计上存在一定的缺陷：卡尔曼滤波的增益矩阵是在线更新的，存在因计算负担过大而导致系统不稳定以致预测失败的情况[10]。同时，卡尔曼滤波需知道系统噪声和测量噪声的协方差矩阵，即噪声的统计学特征。当噪声的分布情况不能有效辨识或辨识误差较大时，预测结果的准确性将受到影响。

针对上述缺陷，本文以龙伯格（Luenberger）观测器[16]代替卡尔曼滤波作为模型设计对象。龙伯格观测器是一种有效解决动态系统控制率问题的方法，设计龙伯格观测器的初衷是为了获取模型所需的系统状态变量。这些变量本身很难直接得到，但在实际控制系统中又有明显的利用价值，基于状态空间方程建立的龙伯格观测器可将系统的输入值与输出值转化为系统状态变量以满足模型需求。龙伯格观测器结构简易，性能表现良好，控制效果优异，在工业控制工程、电液控制系统和前馈控制策略中，选择合适的反馈增益实现估计值和系统被估计值的零误差，从而得到理想的系统状态量[17]。与卡尔曼滤波方法相比，龙伯格观测器离线计算增益，既能降低计算复杂度，又能规避在线更新增益的不稳定情况。

借鉴龙伯格观测器在控制领域中采取合适的增益反馈实现系统零误差，本文采用线性矩阵不等式（Linear Matrix Inequality，LMI）技术计算增益，同时在计算过程中引入抑制噪声的设计条件，尽可能减少噪声对预警结果精确度的影响。有学者研究发现，线性矩阵不等式可用于解决非线性时滞的稳定性等工程控制问题[18]。后期，学者提出多种线性矩阵不等式数值解法，包括替代凸投影算法、内点法等。內点法又分为中心点法、投影法、原始对偶法，其共同思路都是把线性矩阵不等式问题看成凸优化问题处理。1995年矩阵实验室（Matlab）集成了线性矩阵不等式工具箱（LMI Toolbox），这使得高维的线性矩阵不等式计算变成可能，同时也推动了运用线性矩阵不等式解决系统与控制问题的热潮。

基于这两个理论在数学与控制领域的优秀表现，本文创新性地将龙伯格观测器与线性矩阵不等式技术相结合设计了类龙伯格预测器，探究其在财务领域的适用性。相比传统的卡尔曼滤波预测设计，本文的创新点如下：第一，类龙伯格预测器采用时不变的增益矩阵L，不需要实时在线更新计算，一方面降低计算复杂度，另一方面能有效保证预测系统的稳定性，规避因在线计算而造成系统不稳定的情况；第二，类龙伯格预测器无需知道系统噪声和测量噪声的协方差矩阵，因此当噪声辨识误差较大时，本文的方法依然具有较高的精确性；第三，预测系统的增益矩阵可利用Matlab中的线性矩阵不等式工具箱（LMI Toolbox）进行高效求解。

本文设计类龙伯格预测器应用于财务困境预警体系，基于龙伯格观测器理论构建类龙伯格预测系统，并运用线性矩阵不等式技术计算增益；将我国电力企业财务指标与模型相结合，同时对数据进行预处理和主成分分析；对比卡尔曼滤波方法，验证类龙伯格预测器对财务状态的跟踪和预测效果。

对全文所用到的符号做出如下解释。Rn表示n维的欧几里德空间，x∈Rn和A∈Rn×n分别代表一个n维的向量x和一个n×n维的矩阵A。矩阵P？酆0（P？刍0）表示P是一个正定（负定）的矩阵。AT为矩阵A的矩阵转置。0和I分别为合适维度的全零矩阵和单位矩阵。在一个对称矩阵中，？觹表示对应位置的元素可以由矩阵的对称性得到，例如：

■？圳■

二、预警体系设计

类龙伯格预测器是一种时域方法，它基于系统状态空间方程的构造，利用系统中的可测量和观测量误差作为系统反馈，通过选择合适的反馈增益使得反馈误差迅速逼近零，以此获得待观测量。类龙伯格预测器的关键技术之一是状态空间方程。在动态数学中，状态空间方程描述动态系统可分为三个步骤：引出状态变量、建立状态方程、建立用于观测各状态的测量方程。

本文用状态方程和测量方程构造财务困境动态预测方程组，系统中用于表征目标各时间域的最小内部变量组xk∈Rn以列向量呈现，式中x1，x2，…，xn分别对应x的n维度状态变量：

xk=x1，kx2，k■xn，k

状态空间即状态变量的集合，状态变量的维数等同于状态空间的维数。其中状态方程用于表征目标各时期财务指标间的联系，测量方程用于表征目标财务指标与财务状态的关联。引入时间序列的状态空间方程可列式为：

状态方程：

xk=Axk-1+wk-1          （1）

测量方程：

Zk=Hxk+vk           （2）

在式1和式2中，xk∈Rn是状态向量；zk∈Rp是测量向量；wk∈Rn是系统噪声向量；vk∈Rp是测量噪声向量；A∈Rn×n是状态转移矩阵；H∈Rp×n是测量矩阵。

（一）预警系统设计

1.类龙伯格预测器设计

不同于传统的基于卡尔曼滤波技术的动态系统预警方法[8-15]，本文设计全新的财务困境预测系统，即类龙伯格预测系统。该系统由如下两个子模型构成，即式3、式4。

财务过程状态预测模型：

■k+1=A■k+L（zk-H■k）        （3）

财务困境判别模型：

■k+1=H■k+1             （4）

其中，■k+1为财务状态的预测值，■k+1为根据状态预测值得到的困境判別变量，L∈Rn×p为类龙伯格预测器增益矩阵。

为了保证财务过程状态向量的估计值■k不断趋近于真实的状态值（■（xk-■k）=0），进而能够实现判别财务困境的目的，式3需要满足稳定且不断收敛的设计条件。定义ek=xk-■k为预测系统预测误差，那么期望的设计条件也等价于系统的动态误差系统稳定收敛（■ek=0），由定义可知：

ek+1=xk+1-■k+1          （5）

在式5中带入式1和式3可得：

ek+1=Axk+wk-（A■k+L（zk-H■k））

整理可得到预警系统的动态误差表达式：

ek+1=（A-LH）ek+wk-Lvk        （6）

2.增益矩阵计算

为了实时有效地预警财务困境，需要寻找合适的预警系统增益矩阵，使得预测的误差系统稳定且收敛。本节将寻找增益矩阵的问题转化为线性矩阵不等式的求解问题，在实现预测要求的同时，有效克服了传统基于卡尔曼滤波方法需要在每个时刻k计算预测增益矩阵的缺陷。接下来将提出基于线性矩阵不等式技术[18]计算财务过程状态预测模型式3中增益矩阵L的定理并给出相应证明过程。

定理1：若存在对称正定矩阵P∈Rn×n、矩阵W∈Rn×p以及标量γ>0，使得线性矩阵不等式7和式8成立。

P？酆0          （7）

■？刍0  （8）

那么，所设计的财务困境预警系统模型式3、式4是稳定收敛的，并且系统的动态误差满足如下欧几里德范数条件。

■<γ■           （9）

预警系统模型式3、式4的增益可由式10计算得到：

L=P-1W             （10）

为了简化证明过程，式6可简写为：

ek+1=（A-LH）ek+Fδk    （11）

其中，F=[In-L]，δk=wkvk。

分析系统稳定性时，本文首先选取能量函数Vk=e■■Pek，其中，P为合适维度的正定对称权重矩阵。若误差系统式11的能量不断衰减，则可以认为该系统稳定且收敛的，因为本文所考虑的财务困境预警系统模型式3、式4为离散数学模型，那么误差系统能量不断衰减用数学形式可表示为：

ΔV=Vk+1-Vk<0    （12）

即动态系统能量的差分函数始终小于零。考虑到Vk=e■■Pek和Vk+1=e■■Pek+1，同时将式11带入式12可得：

ΔV=（e■■（A-LH）T+δ■■FT）P×（（A-LH））ek+Fδk）-e■■

Pek   （13）

若式13对于k≥0始终满足小于零的条件，则动态误差系统式11是稳定的。但是考虑到状态空间系统模型式1、式2中存在未知噪声（系统噪声wk和测量噪声vk）的干扰，在设计类龙伯格预测系统时需要考虑抑制噪声的设计条件。若要满足式9所提出的范数条件，则需要能量函数的差分（ΔV）满足：

ΔV<-e■■ek+γ2δ■■δk

将式13结果带入可得到：

（e■■（A-LH）T+δ■■FT）P（（A-LH）ek-1+Fδk-1）-e■■Pek-1+e■■ek-1-γ2δ■■δk-1<0

将上式写为矩阵的形式，即：

ek-1vk-1■■ek-1■k-1<0  （14）

其中，

？渍1=（A-LH）TP（A-LH）-P+I

？渍2=（A-LH）TPF

？渍3=FTP（A-LH）

？渍4=FTPF-γ2I

观察可知，式14为二次型形式，故式14成立等价于：

■？刍0    （15）

根据矩阵Schur补引理[19]，由式15继续推导可以得到：

■？刍0

由定义可知，F[In -L]，对上式进一步推导可得

■？刍0

不难发现，当前所得到的不等式为非线性的矩阵不等式（即存在待求得权重矩阵P和增益矩阵L以乘积PL的形式出现），求解上存在一定难度，故令W=PL∈Rn×p，可得到线性矩阵不等式8。

（二）卡尔曼滤波算法

作为类龙伯格预测器的对照组，基于卡尔曼滤波的预警方法同样依赖于状态空间模型式1和式2，并且在应用卡尔曼优化迭代算法时需要提供系统噪声（wk）和测量噪声（vk）的协方差矩阵，故需假定wk和vk都是均值为零、相互独立并且符合正态分布的高斯白噪声序列，则其协方差矩阵分别定义为Q和R，用公式可表示为：

E[wk]=0，E[wkw■■]=Q

E[vk]=0，E[vkv■■]=R

E[wkv■■]=E[vkw■■]=0

参照张东等[14]设计的财务危机预警机制，本文基于卡尔曼滤波的算法可概括为如下五个步骤。

第一步，假定k-1时最优估计■■已知，进行一步预测：

■■=A■■■

第二步，计算一步预测误差方差矩阵：

P■=A■P■A■■+Qk-1

第三步，计算卡尔曼增益矩阵：

Kk=P■H■■[HkP■H■■+Rk]-1

其中，K为基于卡尔曼滤波的财务困境预警所需的增益，本文类龙伯格预测器所用增益为L。

第四步，基于卡尔曼增益，结合最小均方误差原则修正第一步的预测结果■■，得到最优估计值：

■■=■■+Kk[Zk-Hk■■]

第五步，计算最优估计值■■的误差方差矩阵：

P■=[I-KkHk]P■

卡尔曼滤波在随机线性離散系统中的滤波计算是不断重复预测与修正的递归过程，类龙伯格预测器的预测过程与之类似，但两者仍存在以下区别：（1）本文所用方法以时不变的增益矩阵计算结果，而基于卡尔曼滤波方法的增益矩阵需要不断更新[14]；（2）本文方法在预测时不涉及协方差矩阵Q和R的计算，而基于卡尔曼滤波方法的预测效果与噪声分布情况（即Q、R）能否有效辨识高度相关。这两点都会对最终的测量结果造成影响，因此，可将卡尔曼滤波预测结果设置为对照组对比两者的预测精准度。

三、实证分析

利用我国电力企业的财务指标对上文所设计的类龙伯格预测器展开印证。首先进行样本数据的筛选；其次对数据做指标一致性和无量纲化处理，通过主成分分析得到公司综合得分；最后界定模型参数和阈值，为财务困境预警分析做准备[12]。

（一）样本筛选

电力行业的碳排放强度一直远高于其他行业，习近平总书记多次强调要加速绿色环保发展，革新高碳产业技术，提倡资源高效利用。未来市场局势变幻莫测，技术革新的同时往往伴随着市场经济下滑等风险。因此，基于财务指标对电力企业展开财务困境预警将具有较高的现实意义。电力企业本身具有技术成熟度高、知识体系全面、发展趋势稳定的行业特征，利用公开数据可以较为准确地衡量不同时期电力企业的发展变化。本文选取沪深两市电力企业为研究对象，依据现有财务指标进行财务困境预警研究。

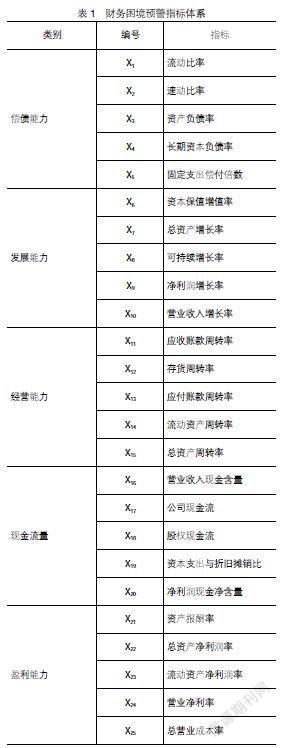
本文参考庄倩等[11]从偿债能力、发展能力、经营能力、现金流量、盈利能力5个财务类别中筛选资产负债率、可持续增长率、营业净利率等25项指标，从电力企业中挑选？觹ST公司和健康公司作为研究对象，考虑季节波动性大、半年度指标参考价值不高等因素，以一年为一个周期，将公司被？觹ST当期记为k，向前追溯10期，分别对应k-1，k-2，…，k-10，用于各年财务状态的记录和对比。

本文数据主要取自国泰安数据库，对于缺失数据通过查阅公司年报等资料进行了核实和补充。最终选取32家？觹ST公司和32家健康公司，将每家公司为期11期的25项财务指标（指标体系见表1）作为样本数据。

（二）数据分析

1.指标预处理

财务困境预警结果由各指标所表达的信息决定，但不同指标数值大小与其表达信息的效果并不一致，即存在正负指标混杂的情况，需对其进行指标一致化处理。同时，指标的单位不同，则数据之间不具备可比性，可通过无量纲化处理，在保留数据差异性的同时将数值确定在[0，1]之间。

（1）正指标预处理公式

X'j=■

（2）负指标预处理公式

X'j=■

式中，Xmax和Xmin为该指标对应公司各年份财务状态的最高值与最低值，Xj和X'j为该指标预处理前后的数值。

2.主成分分析

为反映电力企业的真实情况，指标的选择需全面且有代表性。但若处理所有的数据不仅会导致信息重叠，指标间的多重线性关系，还会引起较大误差，增加预测结果的不确定性和复杂程度。因此，本文选择主成分分析法，不仅能减少区别度不高的冗余指标个数，还能尽可能地保留原有数据信息。主成分辨别时可依据两项原则：（1）特征值>1；（2）累计贡献率>97%，可较好地实现数据降维目的。最终，本文使用Matlab R2018b提取每家公司相应的主成分。受篇幅限制，仅将？觹ST东方主成分分析结果（表2）呈现于文中。

在确认？觹ST东方主成分个数的同时，还可通过主成分分析得出基于这6个主成分11期的Z得分。依据主成分贡献度数值和Z得分对应权重计算最终的综合得分，得到公司不同时期的财务状态。

（三）参数估计

若要进行有效预警，需要对式3和式4中的参数A和H进行参数辨识。另外，虽然本文提出的预测方法无需知道噪声的统计学特征，但为了对比张东等[14]所用方法的预测效果，系统噪声协方差矩阵（Q）、测量噪声协方差矩阵（R）也需要通过辨识得到，同时本文沿用其极大似然估计方法辨识系统参数。以？觹ST东方公司的综合得分为例，用Matlab R2018b计算可得出A=-0.153，H=1，对卡尔曼滤波预测模型中的协方差矩阵可辨识为Q=0.638，R=0。

（四）阈值确定

财务困境预警是依据财务判别阈值对不同时刻的财务状态做出相应预警信号的，因此如何设置合理的阈值对预测准确度而言至关重要。本文依照中国证券监督管理委员会发布的“针对财务状况异常”的界定标准，借鉴庄倩等[13]的统计分析法设立本文财务困境判断阈值，在95%置信水平计算财务困境的置信上下限。

置信上限=XNST-za/2■

置信下限=XST+za/2■

式中，XNST和XST分别指样本中所有？觹ST公司和健康公司财务状态的平均值，za/2为置信系数，■和■分别指样本中所有？觹ST公司和健康公司财务状态的标准差。

利用Matlab R2018b计算得到财务困境判断阈值：置信上限为-1.079，置信下限为-2.232。当预测值高于-1.079时，可判定该时刻财务状态健康；当预测值介于-1.079和-2.232之间时，可判定该时刻公司面临轻度财务困境；当预测值低于-2.232时，可判定该时刻公司陷入重度财务困境，公司必须及时管控风险，否则将面临破产。

四、财务困境预警效果分析

（一）预测结果动态分析

本文对64家样本公司进行动态预测，参照张东等[14]文献中的模型参数设定卡尔曼滤波对照组，并与本文所用方法对照呈现于图中，受篇幅限制仅呈现4家财务状态预测结果（图1—图4），并在本节最后展示全部公司的财务预警正确率。

本文的方法是针对基于卡尔曼滤波方法在噪声分布问题上存在的缺陷而设计的，为突出本文设计方法的预测优势，对？觹ST华电进行特殊处理（对噪声协方差矩阵设定50%的不确定性）。同时以曲线图展现预警结果，可更直观地展现数据跟踪和预警结果。

1.？觹ST公司预测结果

图1为？觹ST东方公司，该公司在2008年（k-2）以前财务状况一直呈良好波动的发展趋势，但在2009年（k-1）财务变化趋势陡降，数值由-0.786跌落至-3.689，陷入重度财务困境；2010年（k）状态略微好转，但仍低于置信下限值。相比之下，基于卡尔曼滤波的预测值虽整体趋势与真实值保持一致，但当财务状态出现较大变动时，预测效果变差。该公司2010年被沪深证券标记？觹ST，而通过模型可以提早一年给出预警，也证明了类龙伯格预测器的良好表现。

2.健康公司预测结果

图2和图3是对皖能电力和宝新能源的预测，虽都为健康公司，但这两家公司的财务状态并不相似。皖能电力自2002年（k-10）以来，虽在2008年（k-4）存在财务状态下滑的情况，但整体趋势都是稳步上升；而宝新能源虽然还未被标记成？觹ST，但在2017年（k-2）和2018年（k-1）数值都处于重度财务困境的边缘，亟须得到企业的关注。宝新能源应当攻克现有难题，努力调整公司运营和财务状态，规避财务困境。

从图2和图3中不难发现，两个模型对企业的财务状况都进行了较好的跟踪和预测。对皖能电力而言，两种预测方法都能精准地体现财务变化趋势，辨识出企业不断上升的财务状态。对宝新能源公司而言，虽并未标记？觹ST，但预测结果显示其财务状态并不乐观，这说明本文所用方法对一些尚处在“健康”状态的公司同样具有一定的警示作用。

3.特殊处理后预测结果

图4和图5为？觹ST华电的特殊处理前后对比图，此处的特殊处理为参数A和H保持不变，系统噪声（wk）和测量噪声（vk）对应的协方差矩阵Q和R各设定50%的不确定性，即模拟噪声误差对预警效果带来的影响。如图所示，两种预测方法原先都有很好的预警效果，特殊处理后，类龙伯格预测器的预测曲线几乎没有变化，而卡尔曼滤波方法无法辨识出重度财务困境，失去了预警效果。

噪声误差是一种客观存在的未知干扰，数学建模无法保证每次都能得到最优结果，当系统中的噪声存在较大误差时，轻则干扰预测结果精确度，重则严重偏离真实的模型动态。鉴于类龙伯格预测器无需系统噪声和测量噪声的协方差矩阵，因此当噪声的分布情况不能有效辨识或辨识误差较大时，该方法的预测结果依然具有较高精确性。

（二）预警正确率分析

本文选取样本32家？觹ST公司和32家健康公司应用分类识别错误率对本次预警系统正确率进行测试。参考孙晓琳[15]采用的错误分类识别规定如下：当一家？觹ST公司被错误识别为健康公司时，可认为属于型I类错误；当一家健康公司被错误识别为？觹ST公司时，可认为属于型II类错误。两种预警模型的识别正确率见表3。

对比预警模型的识别正确率，可发现两种模型都较好地实现了对财务状态实际得分的追踪和预警。而本文方法的优势在于：当噪声分布情况不能有效辨识或辨识误差較大时，依旧拥有较好的预测水平。建模、测量手段，甚至是财务数据真实性、市场波动等因素都会使得系统存在较大误差，故本文提出的预警方法在兼顾了预测性能和设计复杂度的同时，还具有相对较强的可适用性。

五、结论

针对财务动态预警中存在的噪声误差、在线计算量大等问题，本文创新性地设计了类龙伯格预测器模型，对电力企业财务状态展开预测，并设置卡尔曼滤波方法作为对照组。依据分析结果可知，类龙伯格预测器在财务领域具有较高的实践价值，同时在处理噪声和增益方面比卡尔曼滤波更具优势，预测成本小，预警正确率也更高。

总的来看，实验结果大致符合建模预期。考虑到本文首次基于龙伯格观测器与线性矩阵不等式技术设计类龙伯格预测器进行财务困境预警，缺少与现有管理系统的有机结合，在未来可作为学习研究方向继续挖掘类龙伯格预测器在财务领域的潜在价值。

【参考文献】

［1］ GILSON S C.Management turnover and financial distress［J］.Journal of Financial Economics，1989，25（2）：241-262.

［2］ JOHN T A.Accounting measures of corporate liquidity，leverage，and costs of financial distress［J］.Financial Management，1993，22（3）：91-100.

［3］ PURI M，ROCHOLL J，STEFFEN S.Global retail lending in the aftermath of the US financial crisis：distinguishing between supply and demand effects［J］.Journal of Financial Economics，2011，100（3）：556-578.

［4］ LIN T H.A cross model study of corporate financial distress prediction in Taiwan：multiple discriminant analysis，logit，probit and neural networks models［J］.Neurocomputing，2009，72（16-18）：3507-3516.

［5］ CHEN M Y.Predicting corporate financial distress based on integration of decision tree classification and logistic regression［J］.Expert Systems with Applications，2011，38（9）：11261-11272.

［6］ LI Y，MA W.Applications of artificial neural networks in financial economics：a survey［C］.2010 International Symposium on Computational Intelligence and Design，2010.

［7］ OZBEK L，OZLALE U.Employing the extended Kalman filter in measuring the output gap［J］.Journal of Economic Dynamics and Control，2005，29（9）：1611-1622.

［8］ 孙晓琳，田也壮，王文彬.基于Kalman滤波的企业财务危机动态预警模型［J］.系统管理学报，2010（4）：408-414.

［9］ 庄倩.基于卡尔曼滤波的财务困境预测动态性研究［M］.南京：东南大学出版社，2016.

［10］ 潘雅琼，刘艳.科技型企业财务危机预警研究——基于生存分析法［J］.会计之友，2021（8）：64-70.

［11］ 庄倩，陈良华.基于卡尔曼滤波的企业财务困境动态预警模型［J］.统计与决策，2015（24）：190-192.

［12］ 吴树畅，张雪，于静.经营风险与财务杠杆关系研究——基于异质性负债视角［J］.会计之友，2021（19）：59-64.

［13］ 庄倩，陈良华.财务困境理论的预测动态性改进与应用［J］.审计与经济研究，2014，29（5）：69-76.

［14］ 张东，姚乔茜，王樂，等.基于卡尔曼滤波的财务困境预测方法与应用研究——以电力企业为例［J］.东南大学学报（哲学社会科学版），2017（5）：132-140.

［15］ 孙晓琳.基于状态空间的财务危机动态预警模型在中国的实证研究［J］.中国软科学，2013（4）：140-147.

［16］ LUENBERGER D.An introduction to observers［J］.IEEE Transactions on Automatic Control，1971，16（6）：596-602.

［17］ 任炜杰，郭胜辉，朱树先.无人驾驶转向预瞄控制系统状态区间估计［J］.控制工程，2021，28（9）：1773-1779.

［18］ 杨晓光，张庆灵，靖新.内点法在解线性矩阵不等式问题中的应用［C］.中国数学力学物理学高新技术交叉研究学会第十二届学术年会论文集，2008.

［19］ 俞立.鲁棒控制：线性矩阵不等式处理方法［M］.北京：清华大学出版社，2002.