基于SDP图像和MobilenetV2的滚动轴承故障诊断*

刘昕宇，姜长泓，王其铭，张同晖

(长春工业大学电气与电子工程学院，长春 130012)

0 引言

滚动轴承作为旋转机械的关键零件，起着承受载荷与传递动能的作用，被誉为“工业的关节”。但滚动轴承长期处于高负荷运转的工况下，这会导致其很容易发生各种故障[1]。滚动轴承一旦发生故障，不仅会造成经济利益损失，甚至会造成安全事故发生。有统计表示，轴承在机械设备中发生的故障占所有故障的30%～40%。所以对轴承的状态进行实时监测，实现故障诊断的智能化，是降低设备维护成本和保证设备可靠运行的必然要求。

故障诊断本质上是一个故障特征提取和识别的过程。许立等[2]将轴承振动信号小波包分解得到多个小波能量矩，并将其作为故障特征输入BP神经网络，实现了圆锥滚子轴承的故障诊断。杨望灿等[3]将齿轮振动信号EEMD分解后模态分量的模糊熵作为故障特征，输入支持向量机(SVM)分类，完成了齿轮的故障诊断。

近年来，随着深度学习在数据开发、图像处理和语音识别等领域的普及[4-6]，端到端的智能故障诊断方法，逐步成为热门研究。CNN作为深度学习的重要分支，能很好的提取特征和抑制过拟合现象。刘伟等[7]使用时域轴承信号作为CNN的输入，完成轴承故障诊断。徐昌玲等[8]将轴向柱塞泵的振动信号制作成样本集,然后输入到CNN中进行信号特征提取和分类，完成轴向柱塞泵的故障诊断。

由于时域信号不能直接反映出故障特征。一些学者试图从图像处理的角度实现设备故障的诊断研究，以提供一种新的诊断思路。DING等[9]利用深度卷积网络识别小波包能量生成的图像的多尺度特征。用于轴承故障诊断。谷玉海等[10]将轴承振动信号经EMD分解后的IMF分量生成频谱图，再将频谱图压缩成二值化图像作为CNN的输入，实现滚动轴承故障诊断。不同于上述图像转换，对称点模式(symmetrized dot pattern，SDP)方法将一维时间序列转换为极坐标下的对称雪花图，图形差异直接反映不同类型的故障特征。SDP方法被应用于机械设备故障的故障诊断。郑一珍等[11]将振动信号EMD分解后的IMF分量和SDP进行特征融合，并用CNN进行识别，完成了轴承保持架的故障诊断。YANG等[12]通过将声音信号时域波形转换为SDP图，诊断出了发动机产生的故障。

CNN网络由于参数和运算量庞大，对计算机硬件要求很高。很多移动、嵌入式设备的硬件条件有限，难以运行这样的模型。轻量级网络(MobileNet)具有参数少、网络模型简单，运算量小等优点，在图像分类领域得到广泛的应用[13-14]。

本文结合SDP图像和Mobilenet在图像识别和特征学习方面的优势，提出了一种滚动轴承故障的智能诊断方法。将轴承振动信号转化为SDP图像，通过MobilenetV2学习和识别不同轴承故障状态下SDP图像的特征，实现滚动轴承的故障诊断。

1 滚动轴承振动信号的SDP图像转化

1.1 轴承振动信号去噪预处理

滚动轴承广泛应用于复杂机械系统中，传感器采集的振动信号是随机且非平稳的。再加上强烈的干扰噪声，采集的轴承振动信号中难以避免地会混入噪声信号。所以在振动信号生成SDP图像之前，对信号进行去噪预处理是很有必要的。

本文采用ICEEMDAN[15]对轴承振动信号进行分解，并保留主要的故障特征分量，对于不太重要的其他分量给予舍弃。具体步骤如下：

步骤1：对初始轴承振动信号x(t)进行ICEEMDAN分解，得到N(N≥5)个模态分量Mi，i=1,2,…,n；

步骤2：计算初始轴承振动信号x(t)与各模态分量Mi的相关系数Ri。相关系数Ri计算公式如下：

(1)

式中，x为初始轴承振动信号；Mi为各模态分量，i=1,2,…,n。

步骤3：计算轴承正常振动信号xnor(t)与各模态分量Mi的相关系数γi；

步骤4：定义联合相关系数ωi为Ri与γi的差值，即ωi=Ri-γi；计算相关系数因子αi，相关系数因子αi表达式为：

(2)

式中，min(ωi)为联合相关系数ωi的最小值；max(ωi)为联合相关系数ωi的最大值，i=1,2,…,n。

步骤5：将αi从大到小排列，对于前5个αi对应的Mi分量进行叠加重构，得到去噪后的轴承振动信号X(t)。将余下的N-5个Mi分量作为干扰噪声并舍去。

1.2 SDP方法

SDP方法的原理是将一维时间序列转换为极坐标下的对称雪花图，即SDP图像。令X={x1,x2,…,xn}为轴承振动信号序列，xi、xi+l为i、i+l时刻对应的轴承振动信号的幅值。l为时间间隔，将xi与xi+l通过一系列坐标变换，使它们成为极坐标U[ri,θi,φi]中的点。图1是SDP方法的原理图。

图1 SDP方法原理图

图中r(i)为极径，Ox为极轴，θ(i)为坐标点沿极轴逆时针旋转角度，φ(i)为沿极轴顺时针旋转角度。

r(i)、θ(i)、φ(i)计算公式如下：

(3)

(4)

(5)

式中，l为间隔参数；xmin、xmax为轴承振动信号幅值的最小值和最大值；θ为镜像平面旋转角度，θ=360°m/n；(m=1,2,…,n)；n为镜像平面个数；ζ为放大因子(ζ≤θ)。

1.3 参数选取

在极坐标空间中，为了更好地区分和显示不同轴承故障信号的特征，参数ζ、θ、l的选择至关重要。θ通常取值是60°。l和ζ选取合理可以提高SDP图像之间的分辨率，从而增大不同类型信号间的差别。通常l的取值为1～10，ζ取值为20°～60°时，生成的SDP图像比较理想。

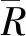
(6)

式中，M为滚动轴承故障信号的SDP图像二维矩阵；N为滚动轴承正常工况信号的SDP图像二维矩阵；m、n为图像二维矩阵的大小。R的取值在0～1之间，当R=0时，表示两张图片完全不同。当R=1时，表示两张图片完全相同。

表1 ζ=30°时，不同l取值下正常工况与各故障工况SDP图像间的相关系数

图2给出了轴承正常工况和故障尺寸0.014 in下不同故障类型的轴承振动信号的SDP图像。从图2能看出，不同故障类型的轴承振动信号在SDP图像上都有不同的表现。具体表现在花瓣的饱满程度、图像中心点的密集程度和花瓣边缘点的稀疏程度等。因此，通过SDP图像的具体表现形式就可以判断轴承的故障类型。

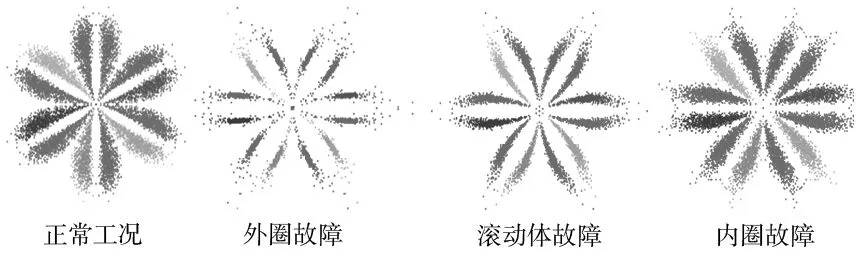
图2 正常工况和3种轴承故障信号的SDP图像

不同故障类型的轴承振动信号的SDP图像在理想状况下的表现差异较大，通过诊断经验便能识别出各类故障。在实际工程中，滚动轴承故障的种类较多，加上采集的轴承振动信号中伴有干扰噪声。这使得生成的SDP图像很难进行人为区别。为了克服这一问题，本文采用MobileNetV2网络对不同类型的轴承信号的SDP图像进行分类识别，从而实现滚动轴承故障智能诊断功能。

2 MobilenetV2网络模型

相比于CNN，MobileNetV2的优点如下：①用深度可分离卷积(depthwise separate convolution，DSC)替代普通卷积，减少了网络计算量和参数。②用ReLU6代替ReLU作为激活函数，避免了因精度缺失，而导致的特征提取和识别的问题。③提出了倒残差结构和线性瓶颈层，在加深网络结构的同时增强了特征提取能力和减小了低维特征信息的损失。

2.1 深度可分离卷积

DSC由逐点卷积(pointwise convolution，PC)与逐深度卷积(deepwise convolution，DC)互相堆叠而成。DC是在每一个图像输入通道上使用1个卷积核进行卷积。PC是1×1的普通卷积，用于特征通道的扩展和压缩。图3是DSC结构图。

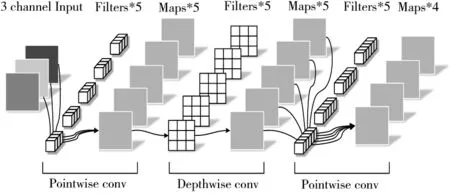
图3 DSC结构图

2.2 激活函数

一般CNN的激活函数为ReLU，但在MobilenetV2中这一函数被替换为ReLU6。ReLU6减少了移动、嵌入式设备用低精度float16描述大范围数值时引起的精度缺失，进而影响特征提取和识别准确率。ReLU6激活函数表达式如下：

ReLu(6)=min(max(x,0),6)

(7)

2.3 倒残差和线性瓶颈

倒残差结构实现了特征的复用，减小了网络模型的结构和计算量。它首先使用1×1的PC将输入的特征图升维，再通过3×3的DC降维，最后输出图片特征。虽然深度可分离卷积和倒残差结构减少了参数量和优化了网络模型，但是也会造成特征信息的丢失，同时ReLU6也会造成低维度特征信息的丢失。为了避免上述问题，MobileNetV2降维后的激活函数ReLU6被线性函数Linear替代，此结构被叫做线性瓶颈。图4给出了倒残差和线性瓶颈的结构图。图中inputb表示数据输入，output表示数据输出。

图4 倒残差和线性瓶颈结构图

2.4 MobilenetV2网络整体结构

本文采用的MobilenetV2网络整体结构如表2所示。

表2 MobilenetV2网络整体结构

在表2中，扩展因子指的是瓶颈结构中通道扩展的倍数，堆叠数指的是重复操作的次数。步幅仅仅作用于重复的瓶颈结构，目的在于改变输出尺寸的大小，其余的步幅均取1，输入图片大小为128×128×3。

3 基于SDP图像和MobileNetV2的滚动轴承故障诊断流程

图5为本文设计的滚动轴承故障诊断方法流程，具体步骤如下：

图5 本文滚动轴承故障诊断方法流程

步骤1：将传感器采集的振动信号ICEEMDAN分解并保留有效故障信息，达到去噪预处理目的；

步骤2：运用对称极坐标变换将去噪后的滚动轴承振动信号转化为SDP图像，并确定生成轴承振动信号SDP图像的最优参数；

步骤3：将生成的SDP图像进行分类并划分为SDP图像训练集和测试集；

步骤4：将SDP图像训练集输入MobilenetV2网络模型中自适应提取故障特征和识别，并调整网络训练参数；

步骤5：将SDP图像测试集输入网络模型中进行测试，得到分类结果，实现滚动轴承的故障诊断。

4 试验

4.1 试验数据

本文验证所提方法的数据来自凯斯西储大学轴承数据中心。滚动轴承故障位置包括外圈、内圈和滚动体。损伤尺寸分为0.021 in、0.014 in、0.007 in，加上正常工况共10类故障状态。每种故障状态生成500个SDP图像样本，并按4:1划分训练和测试集。每1024个采样点生成一张SDP图像样本，每张SDP图片样本大小为128像素×128像素，表3为试验数据集具体描述。

表3 数据集描述

4.2 试验结果

将划分好的SDP图像训练数据集输入MobilenetV2网络模型中，自适应地提取故障特征和进行分类。网络参数设置：学习率为0.001，每次输入样本数量为16，迭代次数为100。实验所得混淆矩阵如图6所示。

图6 模型混淆矩阵

通过图6模型的混淆矩阵能看出，10类故障状态的平均识别准确率为98.2%。其中Normal、IR007、OR021类型故障的诊断正确率均达到了100%。剩余7类故障的诊断正确率相对低一些，但最低也达到了96.1%。这说明本文所提出的滚动轴承故障诊断方法能准确识别适量样本下滚动轴承在不同位置和不同损伤尺度下的10种故障状态。

4.3 对比试验

为了验证所提出的轴承故障诊断方法的准确性和稳定性，笔者设计了3个对比试验。

试验1：提取振动信号的能量比、偏度、峰值因子、脉冲因子、均方根、裕度因子、峭度、波形因子。将所提取特征输入BP神经网络。设置隐层数为3，输出层数为10。此方法用“特征提取+BP表示”。

试验3：将时域滚动轴承振动信号作为输入，输入到一维CNN网络中提取故障特征和分类,实现故障诊断。CNN采用2个卷积层(卷积核大小均为5×5)，2个池化层和2个全连接层。此方法用“1D-CNN”表示。本文提出的诊断方法用“MBV2+SDP图像”表示。

MBV2+SDP图像的诊断方法与其他3种诊断方法的10次随机试验诊断准确率结果如图7所示。

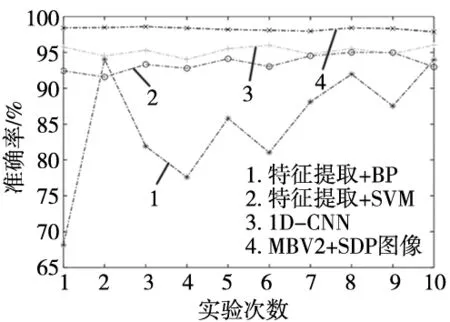
图7 10次随机实验诊断准确率

可以看出，MBV2+SDP图像诊断方法的10次诊断准确率均在97.5%以上且稳定性较好。同时为了准确比较4种方法的诊断精度和稳定性，本文计算了4种方法的10次随机试验的平均诊断准确率和标准差，结果如表4所示。

表4 10次随机实验的平均诊断准确率及其标准差

从表4能看出：在平均诊断正确率方面，MBV2+SDP图像诊断方法最高，达到了98.28%；特征提取+BP诊断方法最低，仅有85.01%。在诊断稳定性方面，MBV2+SDP图像诊断方法最好，其诊断正确率标准差仅为0.23。特征提取+BP诊断方法最差，其诊断正确率标准差高达8.11。对于特征提取+SVM和1D-CNN这两种诊断方法在诊断准确率和稳定性方面均优于特征提取+BP方法，但都不如MBV2+SDP图像诊断方法。以上结果能够说明:在诊断准确率和诊断稳定性方面，MBV2+SDP图像诊断方法相比于其它3种诊断方法具有一定的优势。

4.4 加噪试验

通常，传感器采集的轴承振动信号中难以避免地会混入噪声信号。但某大学的轴承数据是在较为理想的环境下采集到的，振动信号中含噪量很少。为了测试本文所提出方法的抗干扰能力，在10种故障状态的轴承振动信号中加入了5 dB的高斯白噪声。图8为正常工况时轴承振动信号加噪前后的时域波形对比。

图8 轴承正常工况加噪前后时域波形对比

可以看出，加入高斯白噪声后，图像峰值上出现了一些毛刺，初始信号的波形更加平滑。

图9是滚动轴承正常工况下和故障尺寸0.007 in下3种不同故障信号的SDP图像加入5 dB高斯白噪声前后的对比，从左到右依次为正常工况、0.007 in故障尺寸外圈、滚动体和内圈故障。

(a) 未加入噪声时正常工况和3种故障信号的SDP图像

可以看出，加噪后4种故障信号的SDP图像的花瓣外侧边缘的点都变得更加稀疏。花朵中心的信号点分布有所不同。对于正常工况和0.007 in故障尺寸外圈故障这两种状态的SDP图像，它们的花朵中心点由稀疏变得更加密集。对于0.007 in故障尺寸滚动体故障和内圈故障这2种故障状态的SDP图像，它们的花朵中心的点由密集变得更加稀疏。总体上来看，加噪前后滚动轴承振动信号的SDP图像的轮廓变化不大。说明SDP图像具有一定的抗干扰能力。

为进一步验证噪声对SDP图像特征提取的影响，笔者将加入5db高斯白噪声后的10种滚动轴承故障振动信号按照参数l=2，ζ=30°，θ=60°生成SDP图像。并将生成的SDP图像，按本文表3所述划分SDP图像数据集。网络参数设置为：学习率为0.001，每次输入样本数量为16，迭代次数为100。加噪前后的训练结果如图10所示。

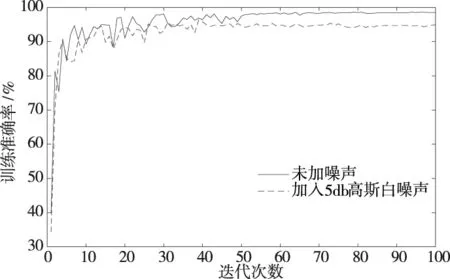
图10 加噪前后训练结果

可以看出，两种样本在训练50次左右时，训练正确率均趋于稳定。在西储大学轴承数据中加入5 dB的高斯白噪声后，模型诊断准确率为94.4%，同不加噪的西储大学轴承数据的诊断准确率98.2%相比，仅下降了3.8%，说明噪声对SDP图像的特征提取有一定的影响，但整体的影响并不大。证明了笔者所设计诊断方法具有一定的抗干扰能力。

5 结论

本文提出了一种基于SDP图像和MobilenetV2的滚动轴承故障诊断方法。将经去噪处理后的轴承振动信号转化为SDP图像，并输入到MobilenetV2网络中自适应地提取故障特征和分类，实现了对滚动轴承不同故障类型的诊断。试验表明：所提诊断方法在诊断正确率和稳定性方面，相比于其它传统的深度学习诊断方法具有一定的优势。在初始轴承信号中加入5 dB的高斯白噪声后，故障识别准确率仍能达到不错的效果。后续还将继续研究如何提高模型的诊断精度和鲁棒性，使其更加精确和智能化。