基于混沌麻雀搜索算法的PMSM直接转矩控制*

左亚辉，谢 源，邹定江，刘世昌，洪炫宇

(上海电机学院电气学院，上海 201306)

0 引言

随着可持续发展的倡议，绿色生活成为了当代主流，新能源汽车使用越发广泛[1]。永磁同步电机(PMSM)因结构特性成为新能源汽车的主要驱动电机，其控制策略成为了当下的研究热点。直接转矩控制(DTC)通过对转矩和磁链的估计，对电机进行控制，因此减少了的坐标变换过程，从而省去复杂的计算工作量，由此直接转矩控制在永磁同步电机中得到了广泛应用[2]。

在直接转矩控制中，常采用的是PI控制器，但其控制性能受到控制参数的影响，难以满足电机在实际中的实时应用[3]。由此如何对PI控制器的控制参数进行合理的优化，对永磁同步电机直接转矩的控制是至关重要的。在起初的PI控制参数是通过人工经验和试凑法进行参数寻优[4]，但这种方式时间较长、效率较低，难以找到最优的PI参数，很难对电机系统进行有效控制。由此有的学者提出应用一些智能算法来进行对PI控制参数的寻优，当前主流的智能算法有神经网络[5]、蚁群算法[6]、遗传算法[7]等。但在采用这些优化算法进行寻优过程，容易出现局部的最优值，收敛速度不快，难以取得较高的控制精度等问题[8]。

根据上诉的问题，本文提出了一种混沌麻雀搜索算法(CSSA)的新型智能算法，对直接转矩控制中的PI控制参数进行寻优。麻雀搜索算法(SSA)相比于其他智能算法具有求解效率高、稳定性好等特点，但在靠近全局最优解时，也容易陷入局部最优的情况。因此提出Sine混沌映射初始化麻雀种群，解决了麻雀搜索算法存在的局部最优，收敛速度较慢的问题。最后通过MATLAB/Simulink仿真实验结果证明，本文基于混沌麻雀搜索算法的直接转矩控制系统，具有很好的动态响应速度和稳定性，同时可以有效抑制电机的转矩和磁链波动。

1 永磁同步电机数学模型

根据文献[9]可以得到PMSM在d-q轴坐标系下的电压数学模型如式(1)所示：

(1)

式中，ud、uq、id、iq分别为PMSM定子电压、电流在d、q轴坐标系下的分量；Ld、Lq分别为PMSM在d、q轴坐标系下的电感分量；ψf为PMSM永磁体磁链；ωe和R分别为PMSM的电角度、定子电阻。根据式(1)可将表贴式PMSM的电磁转矩方程写为：

Te=1.5pnψfiq

(2)

式中，Te为电磁转矩；pn为PMSM的极对数。永磁同步电机直接转矩控制策略主要是对电机的电磁转矩以及磁链进行控制。传统的永磁同步电机直接转矩控制系统中主要使用PI控制来实现对电机转速，转矩以及磁链这3个变量的控制。而控制器性能的优劣将直接影响到系统整体的控制性能，接下来将具体分析不同智能算法对于PI控制器的优化效果。

2 混沌麻雀搜索算法优化PI控制

2.1 基本麻雀搜索算法

麻雀搜索算法(SSA)[10]，主要对麻雀种群的觅食行为和反捕食行为进行模拟，麻雀种群寻找食物的过程也可以表示为一种发现者-加入者模型，并且在此基础上还加入了侦察预警机制。发现者在种群中有着很强的适应度，搜索区域广，在种群中起到搜索和觅食的作用，加入者主要是跟随发现者，其适应度较低。在种群中当预警者发现捕食者时，会为种群发出警告信息。当安全值小于警告值时，发现者会将种群向其他安全的区域进行迁徙，处于种群边缘的麻雀会很快的达到安全范围，而处于种群中间的麻雀将会随机走动，跟随周围的麻雀以此跟随种群[11-13]。

麻雀种群可以用n*d的矩阵表示：

(3)

式中，n为麻雀种群的数量；d为维度。

SSA种群的适应度函数表示如下：

(4)

式中，f为每只麻雀的适应度值。

在麻雀搜索算法中，发现者在种群中有着很好的适应度值，所以在寻找食物的过程中有着向导的作用，为加入者寻找食物提供了方向，发现者的具体位置更新可以由如式(5)所示。

(5)

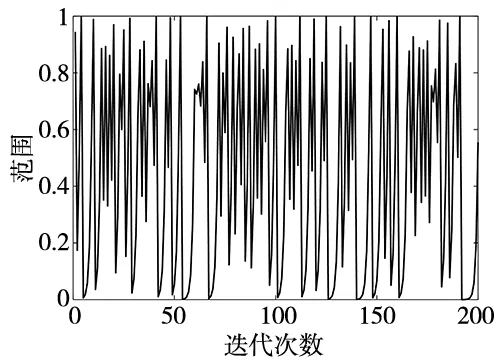
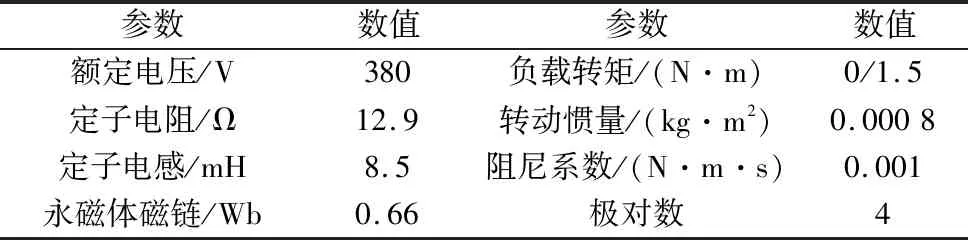
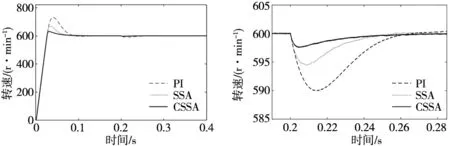
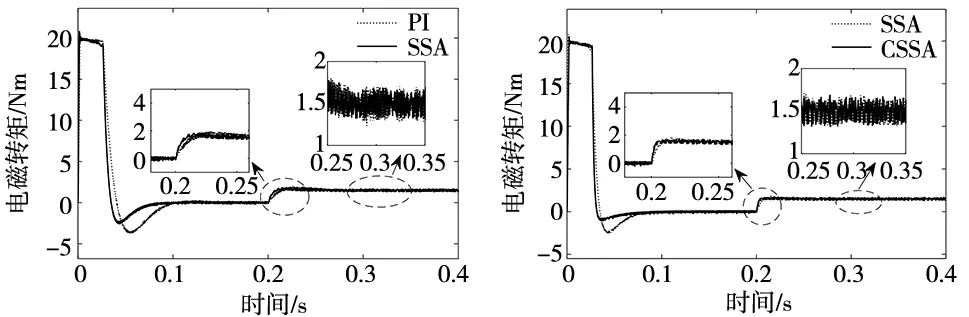
式中，t为算法的迭代数；Xi,j为第i只麻雀在第j维；L为单位行向量；α为[0,1]的随机；NM为最终的迭代次数；Q为标准的正态分布随机数；R2为警告值，并且R2∈[0,1]；ST为安全值，同时取值范围为[0.5,1]。当R2

在种群觅食的过程中，加入者总是跟随着发现者以获取食物，所以加入者位置更新可以表示为：

(6)

式中，Xworst为当前时刻下种群最差的位置；Xq为当前时刻下发现者的最佳位置；D为1×d阶矩阵，其元素为±1的随机值。

在种群中大概有10%～20%的麻雀能够感觉到危险，被称为预警者。位置的更新情况如下所示：

(7)

式中，fi为目前麻雀的适应度；fb为全局最佳位置的适应度；fw为全局最差位置的适应度；Xbest为当前时刻下的全局最佳位置；β为步长的控制参数，β是正态分布的随机数，β的方差等于1，均值等于0；K表示一个范围为[-1,1]的随机数；ε为接近0的常数。在fi≠fb表示为麻雀正处于种群的边缘位置容易遭遇危险。fi=fb表示为位于种群中心区域的麻雀感受到了危险信息，向其他麻雀靠近，来避免被捕食者捕食的风险。

2.2 Sine混沌映射麻雀搜索算法

麻雀搜索算法在搜索范围内随机建立初始种群，这样有可能会使麻雀的种群分布不均匀，搜索范围不足等问题。因为混沌映射有着很好的随机性和规律性，能够对算法的全局搜索能力进行优化，解决算法陷入局部最佳的情况[14]。因此，本文利用Sine混沌映射来对SSA的种群初始化。Sine混沌映射是一种单峰映射，其定义为：

Yi+1=ρsin(πYi)

(8)

(9)

式中，Yi表示为范围为[-1,1]的混沌序列；ρ表示为控制参数；Uj、Lj分别表示为每只麻雀在第j维的上下限。

Sine混沌映射有着很好的混沌特性，Sine混沌映射迭代200次的分布图如图1所示。

图1 Sine映射迭代图

可以看出，Sine映射分布范围在[0,1]，将采用混沌的特性性来对算法的随机初始化改进，使麻雀种群在搜索空间内更加均匀分布，进而可以改善算法容易陷入局部最佳的问题。

2.3 混沌麻雀搜索算法优化PI控制参数

本文采用混沌麻雀搜索算法来对PI控制器的两个参数进行搜索寻优，将比例系数和积分系数作为麻雀位置向量的两个维度，并限定上下边界[15]。发现者不断带领跟随者进行位置更新，逐渐逼近最优的位置，使得永磁同步电机的控制达到最好效果。混沌麻雀搜索算法优化PI控制器的结构图如图2所示。

图2 CSSA优化PI控制器系统结构图

基于CSSA优化PI控制器参数的流程图如图3所示。

图3 CSSA优化PI控制器流程图

3 系统仿真及实验结果

如图4所示为基于混沌麻雀搜索算法的PMSM直接转矩控制系统框图，系统利用空间矢量调制技术替换传统直接转矩中的开关表，通过转速环、磁链环和转矩环对电机系统进行控制。

图4 基于CSSA优化PI的直接转矩控制框图

选用的PMSM参数如表1所示。

表1 永磁同步电机仿真参数

为了验证本文所提出的改进控制策略的优越性，通过MATLAB/Simulink仿真平台搭建了传统的直接转矩控制系统、基于SSA-PI控制的直接转矩控制系统和基于CSSA-PI控制的直接转矩控制系统。设置控制系统的仿真时间为0.4 s，额定转速为600 r/min，电机在0 N·m情况下启动，并且为了验证抗干扰性，在0.2 s后突加1.5 N·m的负载转矩。算法中设置最大的迭代次数为50，麻雀种群数为10，转速环中Kp、Ki的取值范围均为[0,30]，磁链环中Kp、Ki的取值范围分别为[0,2500]、[0,40000]，转矩环中Kp、Ki的取值范围分别为[0,2000]、[0,1000]。所得仿真结果如图5～图11所示。

图5 SSA与CSSA适应度对比曲线

由图可知，麻雀搜索算法在迭代次数为41，适应度才可以达到收敛，混沌麻雀搜索算法在迭代次数为14，适应度就已达到收纳。由此可以看出CSSA相比于SSA有着更快的迭代速度。

由表2和图6可以得出，相比传统的PI控制器，加入麻雀搜索算法的PI控制器在空载启动的时候，超调量降低了10.22%，调节时间减少了0.011s。采用混沌麻雀搜索算法的PI控制器进一步降低了启动时的超调量和调节时间，使得电机的动态响应能力进一步的提升。

图6 3种控制策略转速对比图 图7 3种控制策略转速局部放大对比图

表2 3种PI控制器空载启动性能

由表3和图7可以看出，在0.2 s时突加负载时，SSA-PI相比于PI控制器动态响应速度更快，转速波动更小，减少了4.5 r/min，到达稳定时间缩短了0.013 s。当采用CSSA-PI控制器时，转速的波动范围进一步缩短为2.2 r/min，同时恢复时间更加的迅速，拥有着更好的抗干扰能力。

表3 3种PI控制器突加负载时性能

图8和图9为3种控制策略永磁同步电机电磁转矩波形对比图。CSSA-PI控制器在启动时，在0.08 s就达到了稳定，而SSA-PI控制器和PI控制器达到稳定的时间分别为0.087 s、0.105 s，相比于这两种控制器达到稳定时间分别下降了0.007 s、0.025 s。在加入负载时，CSSA-PI控制器达到稳定时间为0.207 s，转矩脉动为1.42 N·m～1.67 N·m。SSA-PI控制器达到稳定时间为0.213 s，波动范围为1.43 N·m～1.74 N·m。而PI控制器达到稳定的时间为0.223 s，波动范围为1.42 N·m～1.91 N·m。由此可以得出CSSA-PI控制器相比于其他两种控制器，达到稳定的时间更短，并且转矩的波动范围更小，进而提高了电机系统的控制精度。

图8 PI与SSA电磁转矩对比图 图9 SSA与CSSA电磁转矩对比图

由图10可以看出，PI控制器的磁链波动范围0.648 Wb～0.678 Wb，波动差值为0.03 Wb。SSA-PI控制器的磁链波动范围0.644 Wb～0.68 Wb，波动差值为0.036 Wb。由图11可以得出，CSSA-PI控制器的磁链波动范围0.653 Wb～0.673 Wb，波动差值为0.02 Wb。CSSA-PI控制器相比SSA-PI控制器和PI控制器磁链脉动分别降低了0.016 Wb、0.01 Wb。由此可以看出CSSA-PI控制器对于直接转矩控制中的磁链脉动也有一定的抑制作用。

图10 PI与SSA磁链对比图 图11 SSA与CSSA磁链对比图

4 结论

通过MATLAB/Simulink仿真证明了，相比于传统的直接转矩控制系统，和普通麻雀搜索算法，本文提出的基于混沌麻雀算法的PMSM直接转矩控制系统在各项性能上均有较大提升。

(1)优化后的PMSM直接转矩控制系统各项动态性能指标均得到大幅提升。电机转速，转矩的调节时间，超调量以及上升时间都得到了大幅降低。

(2)优化后的PMSM直接转矩控制系统的稳定性和抗干扰能力也得到一定增强，突加负载后电机的转速，转矩和磁链能够快速恢复到给定值，且转速受负载转矩干扰较小，同时系统的磁链和转矩脉动得到了较好的抑制。