高阶次Caputo 型分数阶微分算子及其图像增强应用
王相海 张文雅 邢俊宇 吕 芳 穆振华
1(辽宁师范大学地理科学学院 辽宁大连 116029)
2(辽宁师范大学数学学院 辽宁大连 116029)
尽管分数阶微积分与整数阶微积分几乎同时期出现,但分数阶微积分不像整数阶微积分一般具有较直观的几何含义和物理意义,这样在发展初期,分数阶微积分由于缺少物理和工程等背景学科的支持,几乎很少受到工程领域界的关注[1-2].随着对分数阶微积分及分数阶微分方程研究的不断深入,特别是当物理及工程领域中遇到的一些实际问题难以通过整数阶微积分和整数阶微分方程准确地反映其复杂特性时,而分数阶微积分具有的诸如记忆性和非局部性等特性可为相应问题的解决奠定很好的数学基础[3-4],分数阶微积分被物理、工程、金融经济和生物学等诸多领域重视并得以应用[5-7].近年来对于图像处理领域,得益于分数阶微积分对图像边缘、纹理信息的独特应用,即分数阶微分可在有效提高图像高频信息的同时,非线性地保留图像的低频信息;而分数阶积分则可在有效提高图像低频信息的同时非线性地保留图像的高频信息[8],使得分数阶微积分被应用于诸如图像增强、图像去噪、图像配准和图像识别等重要领域,取得了很好的处理效果[9-10].
分数阶微积分问题的讨论最早可追溯到Newton和Leibniz 创立的微积分时代,但直到19 世纪末其理论体系才被建立并逐渐发展,直到20 世纪后期分数阶微积分的应用性研究才得以快速发展.不同于传统的整数阶微积分,分数阶微积分的定义通常会依据所研究问题的角度而给出不同的表现形式,目前比较经典的3 种定义形式[11-12]有:G-L(Grünwald-Letnikov)型、R-L(Riemann-Liouville)型和Caputo 型定义.其中,G-L 型分数阶微积分通过对整数阶微积分差分近似公式的极限来定义,该种类型的分数阶微积分将“微分”和“积分”统一为一种表达方式,通过阶数参数的正、负取值来分别表示函数的分数阶微分和分数阶积分,并且具有计算的实值性、连续性和线性等特性,同时可通过卷积运算来完成其数值计算;R-L 型分数阶微积分在一定意义上可以看成是对G-L 型分数阶微积分的改进和扩充,该类型分数阶微积分以变限积分形式给出,这样可通过分部积分公式和Taylor展开对其进行级数表示,从而简化了计算过程,特别对于确定一些简单函数分数的解析解具有较大优势;Caputo 型分数阶微积分也可以看成是G-L 型分数阶微积分的改进,其表现形式也是一种变限积分形式,但不同的是R-L 型分数阶微积分是先积分再微分,而Caputo 型分数阶微积分是先微分再积分,避免了R-L 型的超奇异特性,同时Caputo 定义方便解决分数阶微分方程的初边值问题,从而为工程领域分数阶微积分的有效应用奠定了基础.尽管3 种分数阶微积分的定义从不同角度各有侧重,但其在一定条件下具有等价性,具体理论分析可参见文献[11].
图像增强的目的是有选择地突出图像中的重要特征,同时衰减和抑制图像中不需要的噪声,改善图像质量,为进一步的图像分析和理解奠定基础,图像增强作为图像处理的一个重要分支一直受到重视[13-14].在图像增强过程中,图像的纹理、边缘等有用特征一般都需要保护和增强,而污染的噪声则需要去除.近年来随着基于分数阶微积分图像处理研究的不断深入,越来越多的基于分数阶微分的图像增强方法被提出[15-16].目前基于分数阶微积分的图像增强方法总体包括变换域方法和空间域方法2 大类.变换域方法利用诸如分数Fourier 变换和分数Wavelet 变换等分数变换[17-18]将图像变换到分数频率域,依据各分数变换的特性对频率域系数进行调节以达到图像增强的目的[19-21].由于分数变换具有较强的处理非平稳信号的能力,该类方法通常能很好地提高图像的对比度并获得理想的纹理效果,该类方法的不足在于在对图像进行变换处理的过程中通常会有少量噪声被引入.基于空间域的方法是直接对图像的像素实施分数阶微分操作以实现图像增强[22-25],在实现图像增强的同时避免了噪声的引入,同时具有较快的计算速度.在该类方法中,分数阶微分掩模算子的设计显得尤为重要[22,26-28].然而,由于分数阶微积分图像处理的研究相对较晚,再加上分数阶微积分目前还缺少一个统一的定义形式,而不同定义形式的分数阶微分掩模算子研究进展不平衡且表现出一定的差异性,比如目前相对于G-L 型和R-L 型定义形式,基于Caputo型定义形式的微分掩模算子相对较少,而G-L 型和RL 型形式的分数阶微分尽管对图像纹理细节具有较好的增强效果,但对图像对比度的提升较少[29].这样对适应不同定义形式分数阶微分掩模算子的研究就显得更为有意义,同时也为实际应用所需要.
本文对高阶次Caputo 型分数阶微分算子进行研究,给出了一种基于向前差分的(1,2)阶、(2,3)阶次Caputo 型分数阶微分掩模算子的表现形式,并进行了误差证明,同时对更高阶Caputo 型分数阶微分算子的一般形式进行了分析和讨论;在此基础上将本文所提出的Caputo 型分数阶微分掩模算子应用于图像增强处理中,针对不同阶次、不同大小模板掩模算子进行了图像增强实验.研究结果表明,高阶次Caputo 型分数阶微分算子对于提升图像增强处理的整体质量具有很好的效果,特别对于提升图像的对比度、清晰度和平均梯度具有较为明显的优势.
1 相关工作
1.1 Caputo 型分数阶微分定义及其工程应用分析
在3 种经典的分数阶微积分定义形式中,由意大利物理学家Caputo 提出的Caputo 型分数阶微积分定义是距今最新的一种,其定义形式为[11,30]:
设函数f(x)定义在区间(a,b)上,n为整数,v为(n−1,n)间的分数,定义f(x)的Caputo 型v阶导数为式(1)
这里Γ(·)是Euler Gamma 函数.
Caputo 型导数又可分为左侧Caputo 型导数和右侧Caputo 型导数,具体形式分别如式(2)和式(3)所示:
定义f(x)的Caputo 型v阶积分为[11,31]
如果G-L 型和R-L 型表现形式在分数阶微积分理论和纯数学应用方面发挥着重要作用,Caputo 型表现形式则在现代工程应用方面更加实用,其中的一个主要原因是由于在实际工程应用中所构建的分数阶微分系统通常要求利用物理上可解释的初始条件,比如f(a) ,f′(a)等,而这一点只有Caputo 型表现形式可以做到,具体原因为:
假设0≤n−1
可以看出,Caputo 型微分定义不仅能像G-L 型和R-L型那样提供整数阶导数之间的插值,同时包含Caputo导数的分数阶微分方程的初始条件,呈现出与整数阶微分方程相同的形式,而函数整数阶导数的物理意义是清晰和明确的,这一点对于工程应用领域中选择适当的Laplace 变换公式求解实际问题中的分数阶微分方程十分重要.
1.2 分数阶微分掩模算子分析
随着分数阶微积分算子研究的不断深入,人们对相应掩模算子进行了积极的研究,其中Tiansi 算子作为一种经典的G-L 型分数阶微分掩模算子较早被提出[32-33],该算子依托一元信号f(t)(持续期为[a,t])的G-L 型v阶微分的差分形式(按间隔为1 进行持续时间等分)[34]:
进一步,对二维图像信号,分别以图像的长和宽区间作为x和y方向信号的持续期,选取各自方向信号按式(4)分解的前3 项,采取5×5的分数阶掩模构造了如图1 所示的8 方向的分数阶微分掩模算子-Tiansi 算子,并将其应用于图像的边缘提取,取得了较好的效果.由于Tiansi 算子本身是对分数阶微分的近似表示,这样便为构造更加精准的微分掩模算子提供了进一步改进的空间,比如文献[35]将8 方向的Tiansi 掩模算子分解为8 个具有独立方向的3×3小模板,对于每一个像素可获得按照这8 个模板的加权平均值,通过对这8 个值进行分组处理获得增强幅值的3 种方法,文献[35]方法被用于岩石节理缝隙图像的纹理信息增强取得了较好的效果.
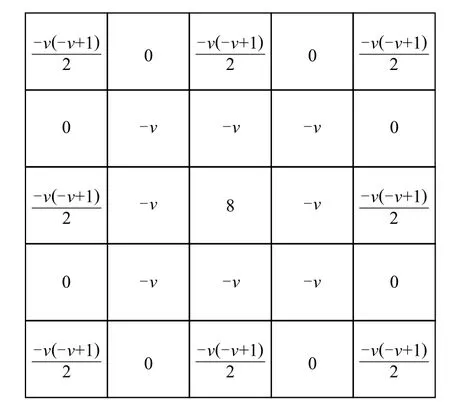
Fig.1 G-L fractional order differential Tiansi operator图1 G-L 型分数阶微分Tiansi 算子
进一步,文献[36]从G-L 型和R-L 型分数阶微分定义的去极限和去积分等近似表示入手,从便于计算和提高精度的角度给出了2 种类型分数阶微分的不同近似表现形式,针对各种近似表现形式的系数构建了一类分数阶微分掩模算子,该类掩模算子共包括6 种形式,每种形式给出了负x轴方向、负y轴方向、正x轴方向、正y轴方向、左下对角线、右上对角线、左上对角线和右下对角线8 个方向的分数微分掩模,取得了较传统整数阶微分算子更好地处理纹理信息等精细结构的能力.该类掩模算子在受到重视的同时,人们也在对其不断地完善和改进,比如文献[37]针对其没有考虑分数阶的优化问题提出一种无监督优化算法用于分数阶参数的选择,并将改进后的掩模算子应用于图像增强[38].此外,Caputo 型分数阶微分算子的数值计算和掩模算子也受到重视,文献[29]从一维信号的Caputo 型分数阶微分定义出发,按照前向差分格式确定其差分近似表达式,并通过将表达式转换为简单的加法、乘法运算将其视为信号与系数函数的卷积,获得卷积模板系数;进一步将此过程推广到二维图像获得8 个方向的卷积模板系数;最后通过将8 个方向的模板系数进行合并形成最终的Caputo 型分数阶微分掩模算子.文献[39]针对左侧Caputo 型导数进行了数值化研究,通过基于分段两次插值逼近实现了一种L1-2 离散方案;而文献[40]则对右侧Caputo 型导数的数值化进行了研究,通过对右侧α(0<α<1)阶Caputo 分数阶导数进行L2-1 离散,获得了逼近格式,这些结果为进一步构造高效的掩模算子奠定了基础.
近年来,人们在不断挖掘有效的分数阶微分掩模算子,将其应用于不同的图像处理领域.比如,文献[41]从G-L 型分数阶微积分定义出发,依据式(2)的近似表示系数和图像像素间的局部相关性构建了8 方向的3×3 掩模,并将其求和,形成最终的3×3 掩模算子,该算子被用于脑部医学核磁共振(magnetic resonance imaging,MRI)图像的增强;文献[42]基于R-L 型分数阶微积分的卷积表示系数,构建了一种具有自适应分数阶优化的R-L 型微分掩模算子,并将其应用于尺度不变特征变换(scale-invariant feature transform,SIFT)算法;文献[43]依据R-L 型分数阶微积分的2阶后向差分表示方案对传统的8 方向微分掩模算子进行了改进并将其应用于指纹图像增强;文献[44]对Caputo 型分数阶微分提出一种基于Lagrange 差值的近似方案,给出了其局部截断误差分析,并将其应用于一类拓展的边值方法来求解问题.
1.3 (0,1)区间分数阶微分掩模算子分析
对于Caputo 型分数阶微分定义(参见式(1)),对于阶数v∈(0,1),此时定义式中的n=1;不失一般性,选取a=0,即f(x)的定义域区间为[0,x],将[0,x]进行N等分(每个等分大小为∆x=x/N),并令xk=k∆x=kx/N,则按照前向差分格式获得相应的一维信号(0,1)区间Caputo 分数阶微分的差分格式(此时可设h=∆x=1)[29]:
其中
进一步,对二维图像f(x,y)分别沿x,y方向进行微分的近似差分近似表示,其中沿x,y方向定义域区间的间隔步长 ∆x和 ∆y均选为1,获得f(x,y) 沿x,y方向(0,1)区间Caputo 型分数阶偏微分的差分格式,其表示如式(7):
为了使掩模算子在图像处理中具有抗旋转性,与上述x,y正方向的分解系数相似,获取0°,45°,90°,135°,180°,225°,270°,315°,共8 个方向的偏导数分解系数,并据此构建如图2 所示的5×5 Caputo 型微分掩模算子.
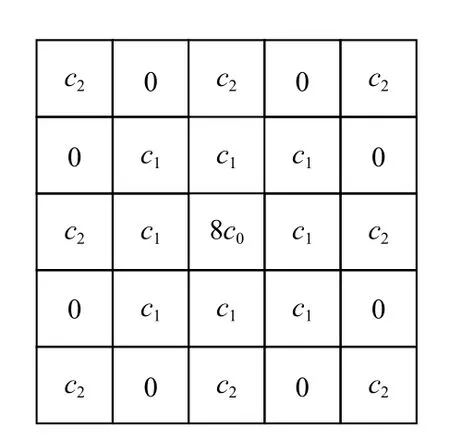
Fig.2 Caputo fractional order differential mask operator with order in (0,1)图2 (0,1)区间Caputo 分数阶微分掩模算子
2 分数阶微积分算子阶数对信号的影响
对于平方可积的能量函数f(x)∈L2(R),其Fourier变换为
对f(x)进行分数阶v(v∈R+)微分[45]:
进一步,由Fourier 变换特性可得
为了进一步分析分数阶微积分中阶数的大小对信号分析的影响,图3 和图4分别依据对v∈(0,3)的分数阶微分算子和v∈(−3,0)的分数阶积分算子的幅频特征曲线进行了绘制,其中横轴代表频率 ω,纵轴代表幅值
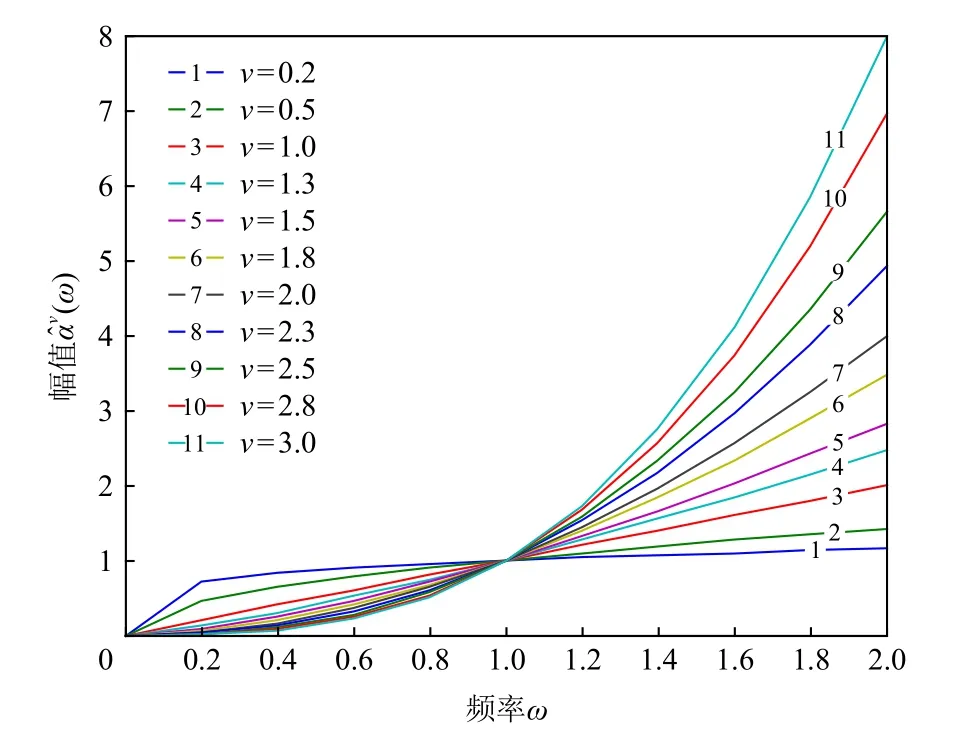
Fig.3 Amplitude frequency characteristic curves of fractional order differential图3 分数阶微分的幅频特征曲线

Fig.4 Amplitude frequency characteristic curves of fractional order integral图4 分数阶积分的幅频特征曲线
由图3 可以看出,对于信号的高频部分(ω>1),分数阶微分算子对信号具有增强作用,且随着阶数的提高,幅值在一定程度上也随之增加,比如属于(1,2)和(2,3)区间阶的分数阶微分算子的高频幅值明显高于(0,1)区间阶的分数微分算子的高频幅值;同时对于信号的低频部分(ω<1),分数阶微分算子对信号具有一定的非线性削减作用,且随着阶数的提高,削减的幅度在一定程度上得以减少,比如属于(2,3)和(1,2)区间阶的分数阶微分算子的低频幅值要低于(0,1)区间阶的分数阶微分算子的低频幅值.这样基于高阶次的分数阶微分算子较低阶次的分数阶微分算子在图像处理过程中总体上具有可更加有效地对高频信息进行区分和对低频信息进行保护的特性,从而为提高诸如在图像增强、图像分割和图像识别等图像处理的质量奠定了基础.
同理由图4 的分数阶积分算子的幅频特征曲线也可获得相应的结论.该算子对于信号低频信息的敏感程度远大于分数阶微分算子信号低频信息的敏感程度,同时可以非线性地对高频信号进行精细化处理,从而为诸如图像去噪等图像处理应用提供了有效工具.
3 高阶次Caputo 分数阶微分算子研究
3.1 (1,2)区间阶 Caputo 分数阶微分掩模算子
对于阶数v∈(1,2)的Caputo 型分数阶微分,其定义为
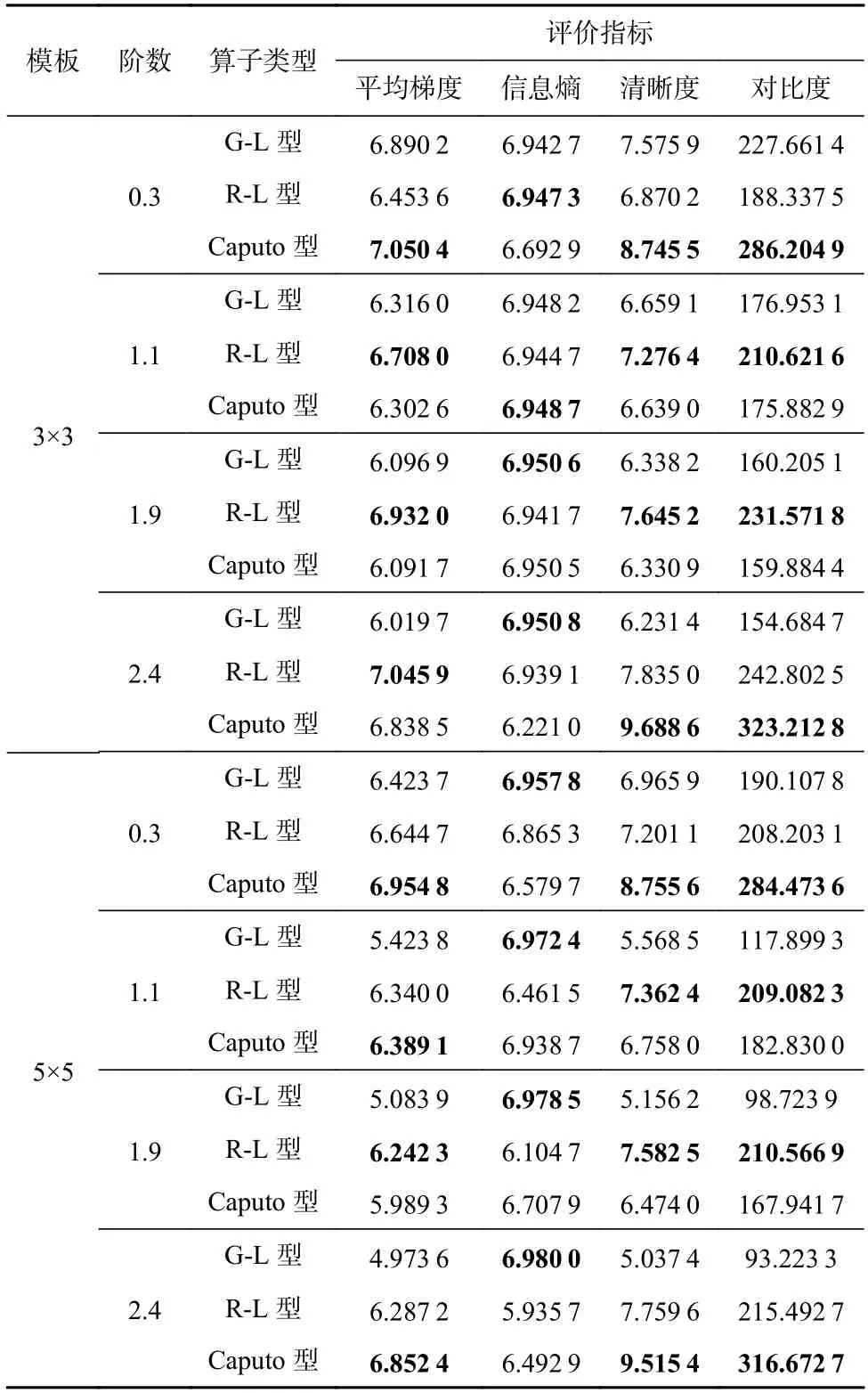
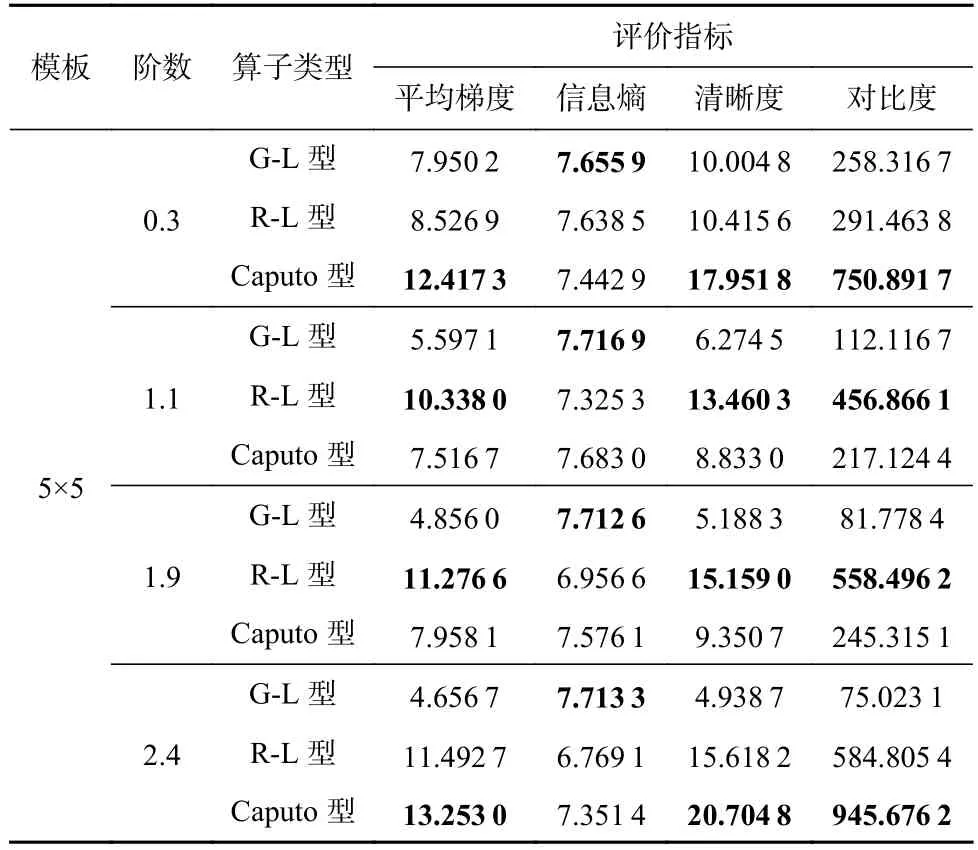
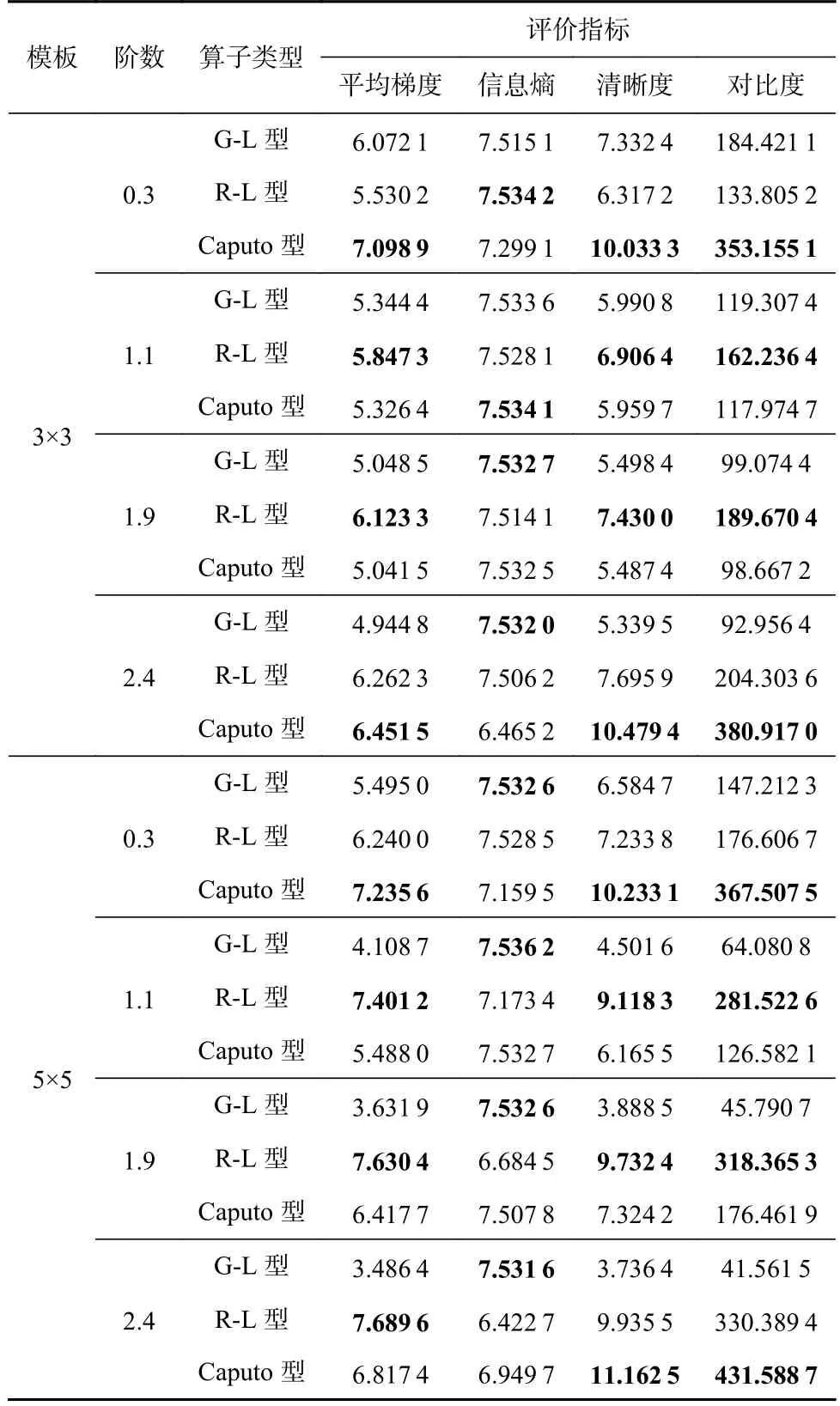
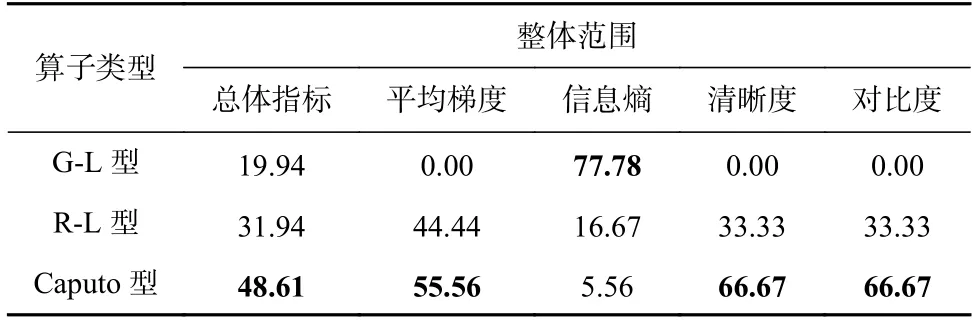
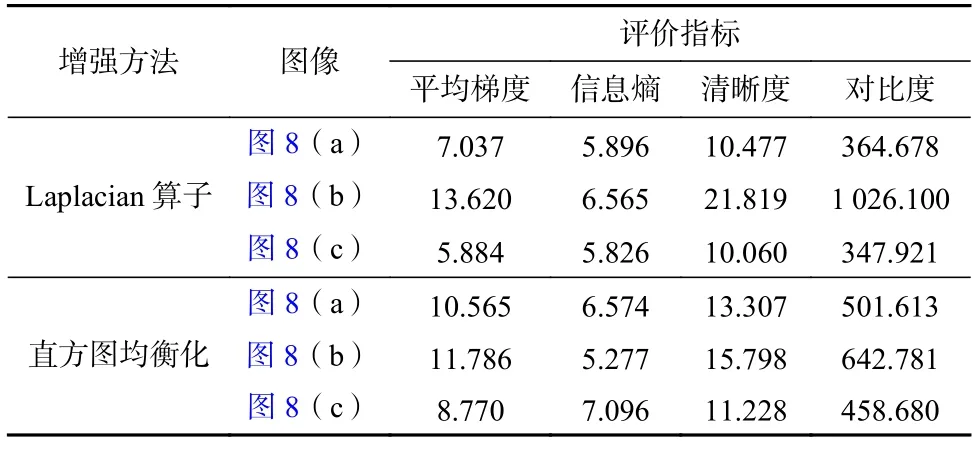
将f(x)的定义域区间[0,x]进行N等分,令h=x/N,记xk=kh,其中k∈{0,1,···,N},0=x0 进一步通过(xN−ξ)进行换元可得 由向前差分格式可得 对于图像信号,相邻像素之间的间距为1,故可令微分步长h=1,从而有n=[x/h]h=1=[x],xk=kh=k,此时式(12)变换为 其中 引理1.设函数f(x)∈C2[0,x],将区间[0,x]进行n等分,令h=x/n,xk=kh,0 ≤k≤n,0=x0 其中 证明.对区间[xk−1,xk]⊂[0,x] 及ξ ∈[xk−1,xk],对f(xn−ξ)进行线性插值,有 进而有 可以看出,一阶向前差分格式可以看成对应端点线性插值的一阶导数. 进一步,有 由分部积分法可得 其中 而由插值余项定理可得 定理1.设函数f(x)∈C3[0,x],将区间[0,x]进行n等分,令h=x/n,xk=kh,0 ≤k≤n,0=x0 证明.令g(x)=f′(x),α=v−1,则有α ∈(0,1),g(x)∈C2[0,x]. 由阶数在(1,2)区间的Caputo 型分数阶微分的定义(参见式(11))可得 由引理有: 对二维图像按对其x和y方向进行分离,可分别获得沿着这2 个方向的式(13)的离散格式,进一步可利用其前3 项分解系数构造如图5 所示的(1,2)区间阶5×5 Caputo 型微分掩模算子. Fig.5 Caputo fractional order differential mask operator with order in (1,2)图5 (1,2)区间Caputo 分数阶微分掩模算子 对于阶数v∈(3,4)区间的分数阶微分,根据定义有: 将区间[0,x]进行n等分,令h=x/n,xk=k h,0 ≤k≤n,即0=x0 由向前差分格式可得 考虑图像处理情况中行或列相邻像素之间单位间距为1,这样离散过程中可选取h=1,从而有xk=kh=k(0 ≤k≤n).此时,式(19)可化简为式(20).由此我们得到阶数在(2,3)区间的Caputo 分数阶微分的离散形式为式(21). 其中 定理2.设函数f(x)∈C4[0,x],将区间[0,x]进行n等分,令h=x/n,xk=kh,0 ≤k≤n,0=x0 其中 证 明.令φ(x)=f′′(x),β=v−2,则 有β ∈(0,1),φ(x)∈C2[0,x]. 由阶数在(3,4)区间的Caputo 型分数阶微分的定义(参见式(15))可得 由引理有 同理对二维图像,可按对其x和y方向进行分离,分别获得沿着这2 个方向的离散格式.在此基础上可构造如下的(2,3)区间阶Caputo 型微分掩模算子: 1)3×3 型掩模算子 取式(17)的前2 项分解系数,即f(x) 和f(x−1)项的系数,按照如图6 所示的形式构造(2,3)区间阶Caputo 微分的3×3 型掩模算子. Fig.6 Caputo fractional order differential 3×3-type mask operator with order in (2,3)图6 (2,3)阶Caputo 分数阶微分3×3型掩模算子 2)5×5 型掩模算子 取式(17)的前3 项分解系数,即f(x) ,f(x−1),f(x−2)项的系数,按照如图7 所示的形式构造(2,3)区间阶Caputo 微分的5×5 型掩模算子,其中 Fig.7 Caputo fractional order differential 5×5-type mask operator with order in (2,3)图7 (2,3)阶Caputo 分数阶微分5×5 型掩模算子 事实上对于式(20)的(2,3)区间的Caputo 分数阶微分的离散形式,理论上可以依据其n+1 系数(参见式(18))构造其(n+1)×(n+1)型的分数阶微分掩模算子,但实际图像处理应用中由于图像所具有的局部相关性,该掩模算子一般不宜过大. 对于v阶(0 将区间[0,x]进行n等分,令h=x/n,xk=kh,0 ≤k≤n,0=x0 进一步按照向前差分格式可得 其中 实际应用中可令h=1,n=[x/h]h=1=[x],则有 由此便可根据m来确定其分数阶微分算子.然而,式(25)的表现形式还是很复杂,从而给具体应用带来困难.本文对其做进一步的简化,给出基于矩阵化的表现形式.为此令 其中Qk为关于参数k的m+2维行向量,Cm为关于参数m的m+2维列向量,即有 简化 式(26)的 计算 中,对Qk中k−(m−i)<0或k−(m−i)>n(i=1,2,···,m−1,m)的情况,令(k−(m−i))m−v=0. 分数阶微分可以增强图像高频部分的幅值并同时非线性保留低频信息,因此分数阶微分算子常被应用于图像增强.具体通过将掩模算子与像素点所对应的区域依次进行卷积操作实现图像的空间滤波. 本文实验中对图像增强质量采用主、客观评价方式评判,其中客观评价采用了平均梯度、信息熵、清晰度和对比度4 种指标.具体计算方法为: 设图像I的大小为M×N,I(i,j)为图像中(i,j)位置处像素的灰度值,其中i=0,1,···,M−1;j=0,1,···,N−1. 2)信息熵(S) S反映图像中的纹理丰富程度,图像越平滑信息熵越小;纹理越丰富信息熵越大.其定义为 其中Pi j是模板内具有与I(i,j)相同灰度值的概率. 3)清晰度(D) D反映图像的局部信息及边界的清晰程度,图像中边缘轮廓越模糊,清晰度越低,而边缘轮廓越清晰,清晰度则越高,其定义为 其中Ix(i,j) 和Iy(i,j)分别表示图像I在x和y方向上的导数. 4)对比度(C) C表示图像从黑到白的渐变层次,对比度越大图像的渐变层次越多,色调越丰富.其计算公式为 其中δ(i,j)=|i−j|表示相邻像素间灰度值的差值,Pδ(i,j)表示相邻像素灰度值差值为δ(i,j)的分布概率.实验图像选择了如图8 所示的3 幅灰度图像. Fig.8 Experimental images图8 实验图像 对于3.2 节中给出的(2,3)阶Caputo 微分掩模算子的表现形式(参见图7),本文依据其对实验图像进行了增强实验,发现增强后的图像在边缘处会出现一些“伪影”现象,并且随着模板尺寸的增大而变得明显.进一步,本文给出了(2,3)阶Caputo 微分掩模算子的其他表现形式(参见图9),其中{e1,e2,e3}参见式(21). Fig.9 The other forms of Caputo differential mask operator图9 Caputo 微分掩模算子的其他种表现形式 图10 列出了利用2 种(2,3)阶Caputo 微分掩模算子模板分别对“轮胎”图像增强后的结果,其中,第1 种模板参见图6、图7;第2 种模板参见图9. 从图10 的实验结果可以看出,第2 种(2,3)阶Caputo 微分掩模算子模板不仅没有“伪影”现象,无论是3×3形式模板,还是5×5形式模板,均能使增强后图像的纹理边缘较原图更加清晰,可以清楚看到轮胎衔接处纹理及凹凸变化处的边缘.值得说明的是第2 种算子模板形式是在第1 种算子模板形式的基础上通过系数“收缩”微调,并通过大量仿真实验验证获得.以下对比实验中关于(2,3)阶Caputo 微分掩模算子均采用了第2 种模板形式. Fig.10 Comparison of image enhancemental effects of two kinds of Caputo differential mask operator templates with order in (2,3)图10 2 种(2,3)阶Caputo 微分掩模算子模板的图像增强效果对比 为了验证本文所提出(1,2),(2,3)区间阶次Caputo型分数阶微分掩模算子的有效性,将其与G-L 型分数阶微分掩模算子[35]、R-L 型分数阶微分掩模算子[46]以及(0,1)区间阶次Caputo 型分数阶微分掩模算子[33]进行了图像增强实验对比.实验环境为:操作系统Windows 10,处理器Inter®CoreTMi7-4790CPU@ 3.60 GHz,内存16.0 GB. 4.3.1 3 种类型算子的对比实验 从主观视觉效果来看(参见图11~13),总体而言Caputo 型掩模算子能够使增强后图像的边缘信息更加丰富,同时图像也更加清晰,R-L 型掩模算子次之,G-L 型掩模算子相对最差;同时对于相同阶数,5×5模板的增强效果总体上要好于3×3模板的增强效果. Fig.11 Enhancemental effects of different differential mask operator templates on Fig.8(a)图11 不同微分掩模算子模板对图8(a)的增强效果 从客观评价指标效果来看,依据统计数据的占优情况(参见表1~3 的黑体数字指标),表4~6 分别对3 种类型掩模算子的总体占优率及分项评价指标占优率进行了统计.从表4~6 统计表可以看出: 1)从表4 中实验的总体指标来看,Caputo 型算子的占优率最高,占48.61%,其次是R-L 型算子,占31.94%,最后是G-L 算子,占19.94%,这与主观评价的结果一致;同时从整体的平均梯度、信息熵、清晰度和对比度来看,G-L 型算子的信息熵的占优率为77.78%,明显高于其他2 种算子,而Caputo 型算子的其他3 项指标占优率均达到了50%以上.2)从表5 中实验的3×3模板和5×5 模板指标分别来看,总体趋势与表4 相一致,特别是G-L 型算子信息熵的占优率在仍延续了占优优势的情况下,5×5 模板的信息熵占优率达到了100%,明显高于3×3 模板信息熵占优率的55.56%.3)从表6 中掩模算子的阶数来看,阶数为0.3 时,Caputo 型算子的平均梯度、清晰度和对比度的占优率均为最高,而G-L 型算子和R-L 型算子的信息熵要高于 Caputo 算子;阶数为1.9 时,R-L 型算子的平均梯度、清晰度和对比度的占优率均为最高,而G-L型算子的信息熵要高于其他2 个算子;阶数为2.4时,Caputo 型算子的平均梯度、清晰度和对比度的占优率呈现最高的情况,而G-L 型算子的信息熵则为最高. Fig.12 Enhancemental effects of different differential mask operator templates on Fig.8 (b)图12 不同微分掩模算子模板对图8(b)的增强效果 4.3.2 与其他类型算子的对比实验 为了进一步说明本文提出的高阶次Caputo 型分数阶微分掩模算子的效果,将其与经典的Laplacian算子和直方图均衡化方法进行了图像增强对比实验. Fig.13 Enhancemental effects of different differential mask operator templates on Fig.8 (c)图13 不同微分掩模算子模板对图8(c)的增强效果 图14 给出了实验图像通过Laplacian 算子和直方图均衡化方法处理后的可视化效果,表7 是与之对应的客观评价指标计算结果.为了更明显突出算法特征,经Laplacian 算子处理后的实验图像并未进行归一化处理. 从实验的视觉效果来看,Laplacian 算子作为经典的整数阶微分算子,在图像增强处理中更倾向于边缘的锐化,对边缘更敏感,但显然对噪声也比较敏感;直方图均衡化作为图像增强的基本方法,其能够提升图像的对比度,且操作可逆,但会导致图像细节的丢失,这一现象在图8(b)的平坦区域体现得较为明显.总体而言高阶次Caputo 型掩模算子能够在对高频信息进行区分的同时对低频信息进行保护,达到更好的效果;而从客观评价指标来看,Laplacian算子与高阶次Caputo 型掩模算子性能指标差距不是很大,且对实验图像的类型要求较为稳定,而不同类型实验图像均对直方图均衡化方法的性能有较大影响. Table 1 Comparison Results of the Objective Indicators of Enhancemental Effects on Fig.8 (a)表1 图8(a)增强效果的客观指标结果对比 Table 2 Comparison Results of the Objective Indicators of Enhancemental effects on Fig.8 (b)表2 图8(b)增强结果的客观指标结果对比 续表 2 Table 3 Comparison Results of the Objective Indicators of Enhancemental Effects on Fig.8 (c)表3 图8(c)增强结果的客观指标结果对比 Table 4 Statistics of Overall Dominance Rate of Objective Indicators of Experimental Images表4 实验图像客观指标总体占优率统计% Table 5 The Dominant Rate Statistics of Objective Indicators of Experimental Images According to the Size of Template表5 按模板大小统计实验图像客观指标占优率% Table 6 The Dominance Rate Statistics of Objective Indicators of Experimental Images According to Different Orders表6 按不同阶数统计实验图像客观指标占优率% Fig.14 Enhancement effects of Laplacian operator and histogram equalization method on experimental images图14 Laplacian 算子和直方图均衡化方法对实验图像的增强效果 Table 7 The Objective Indicators Results of the Enhancemental Effects of Laplacian Operator and Histogram Equalization Method on Experimental Images表7 Laplacian 算子和直方图均衡化方法对实验图像的增强效果客观指标结果 分数阶微积分所具有的记忆性、非局部性等为相应工程问题的解决奠定了很好的数学基础.近年来得益于分数阶微积分对图像边缘、纹理信息的独特应用,其在图像处理领域受到关注.不同于传统的整数阶微积分,分数阶微积分的定义通常会依据所研究问题的角度而呈现不同的表现形式,每种形式又各有侧重.由于分数阶微积分图像处理的研究相对较晚,从目前常见的G-L 型、R-L 型和Caputo 型3种定义形式来看,基于Caputo 型定义形式的微分掩模算子相对较少,而G-L 型和R-L 型形式的分数阶微分尽管对图像纹理细节具有较好的增强效果,但对图像对比度、清晰度的提升相对较弱.目前针对图像处理的Caputo 型微分掩模算子多限于对(0,1)范围内的低阶情况,而对高阶次情况的研究相对较少,本文对(1,2)阶次和(2,3)阶次的Caputo 型微分掩模算子进行了研究,给出了具体掩模算子的表现形式,同时对更高阶Caputo 型分数阶微分算子的一般形式进行了分析和讨论;在此基础上将其应用于图像增强处理中,针对不同阶次、不同模板大小的应用情况进行了实验统计分析和对比.研究结果表明,高阶次Caputo 型分数阶微分算子对于提升图像增强处理的质量,特别是提升图像的对比度、清晰度和平均梯度具有良好的效果. 作者贡献声明:王相海负责提出论文思路、研究工作指导和论文修改;张文雅负责理论推导、实验程序设计及论文撰写;邢俊宇负责定理的证明;吕芳负责理论推导与数据分析;穆振华负责实验结果分析与整理.
3.2 (2,3)区间阶Caputo 型分数阶微分掩模算子

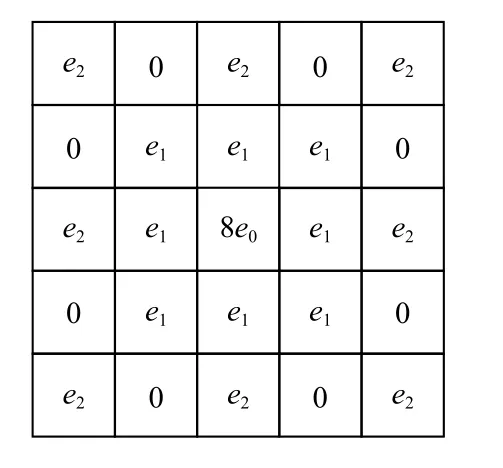
3.3 关于更高阶Caputo 型分数阶微分算子的讨论
4 Caputo 分数阶微分算子的图像增强应用
4.1 评价指标及实验图像

4.2 Caputo 微分掩模算子的其他表现形式


4.3 实验结果与分析







5 结束语

