面向近红外成像超透镜的设计与仿真

王 杰,黎相孟,2,吉卓琪,祝锡晶

(1.中北大学 先进制造技术山西省重点实验室,山西 太原 030051;2.西安交通大学 机械制造系统工程国家重点实验室,陕西 西安 710049)

1 引 言

由超构表面组成的平面光学透镜是近些年来研究的热门课题之一。超构表面是由亚波长尺寸的单元结构按一定规律排列组成[1-4],此结构通过更改相关参数可以实现对光波的精准调控。而由超构表面组成的平面超透镜更是在相位调控,偏振操控,全息成像,负折射率隐身等多方面展示出极大的发展潜力[5-9]。超构透镜的优点在于实现多种调控的同时,也达到了轻量化、微型化、易集成等特点,这意味其投入在实际应用中变得越来越成熟。哈佛大学Capasso团队设计出基于二氧化钛的消色差超表面透镜,针对可见光波段聚焦效率最高达86 %,但基于几何相位调控原理只能实现圆偏振态的入射光聚焦[10]。加州理工学院Faraon课题组提出MEMS可调节超透镜实现了40°视场调控的三维成像[11],并利用偏振相位可调的亚波长空间分辨率全息图谱使光学传输效率从72 %提高到97 %[12]。新加坡国立大学报道了超材料红外光谱仪,通过集成超表面光源、传感器、滤波器和探测器件,实现了便携式环境监测及生物传感器[13]。武汉大学郑兴国教授设计了一种光学超材料的表面织构设计、制造与应用表征,实现了光学防伪和全息成像等功能[14]。上述研究充分表明,超表面透镜在光学元件设计领域具有广泛研究前景。

近红外成像技术是当今社会快速发展的一项高新技术,通过比较待检测对象与背景面板之间的光线强度的差异,来实现对目标的探测识别和轨迹跟踪。近红外成像技术在军事防务、生物医疗、成分检测等领域发挥着不可替代的作用。但是在器件的理论设计与实际制备过程中一直存在差异性问题。针对器件设计应具备轻量化、低成本、易集成的发展趋势,结合硅基超透镜微型、可集成并且支持CMOS工艺可批量生产的特点,本文设计了一款近红外波段的偏振不敏感超透镜。利用有限元数值仿真软件FDTD Solution对超表面单元结构的参数进行优化扫描,并分析得出最优解。由具有最优参数的单元结构形成的超透镜实现聚焦效率为68.3 %,数值孔径(NA)为0.56。研究结果为近红外波段超透镜的高效平面化提供了一定的理论依据。

2 设计原理

在超构透镜的设计中,目前成熟且主流的相位调控原理有传输型相位调控和几何型相位调控,尽管几何相位型在可见光波段的消色差、相位调控能力出众,但由于其对圆偏振态入射光的要求,故本文选择在短波红外应用成熟且对入射光偏振态无特殊要求的传输型相位调控原理。

传输型相位调控超构表面对光波的相位调控是通过光波在其中传播时所产生的光程差来实现的,具体方式是通过调节各周期内单元结构体的占空比来改变结构体的等效折射率,从而达到相位调控的目的[15-17]。光波在传输过程中积累的相位差φ满足以下表达式:

φ=k0nd

(1)

其中,ko=2π/λ表示自由空间的波矢量;λ为入射波在真空中的波长;n为介质的等效折射率;d为传播距离。传统光学透镜通过增加d来扩大相位调控范围,其使用曲面外形既增加了加工难度也不利于集成制造。而超透镜在不改变透镜厚度d的基础上通过调节等效折射率n来实现相位调控,这使得透镜制作实现平面化、批量化成为可能。

结合短波红外波段对材料的要求,本文选择基底材料为高折射率且加工技术成熟的非晶硅,衬底材料为低折射率高透过率的二氧化硅。图1为超透镜工作原理图及单元结构参数示意图。图1中(a)所示,超透镜表面由若干单元结构按照一定规律排列而成,入射的平面波沿Z轴由衬底位置射入,经过基底材料时发生相位突变,平面波变为球面波最终实现焦点处汇聚。图1中(b)和(c)分别为单元结构的俯视图和侧视图。为实现偏正不敏感透镜设计,单元结构应采用对称结构,本文对非晶硅采用加工方式简单、易高效制造的柱状结构；对衬底结构选用易编程操控的方形结构。单元结构的周期为P,纳米硅柱的半径为R,高度为H,这三个参数是影响单元结构相位突变和透过率的主要因素,接下来会经过仿真得到最优参数范围。

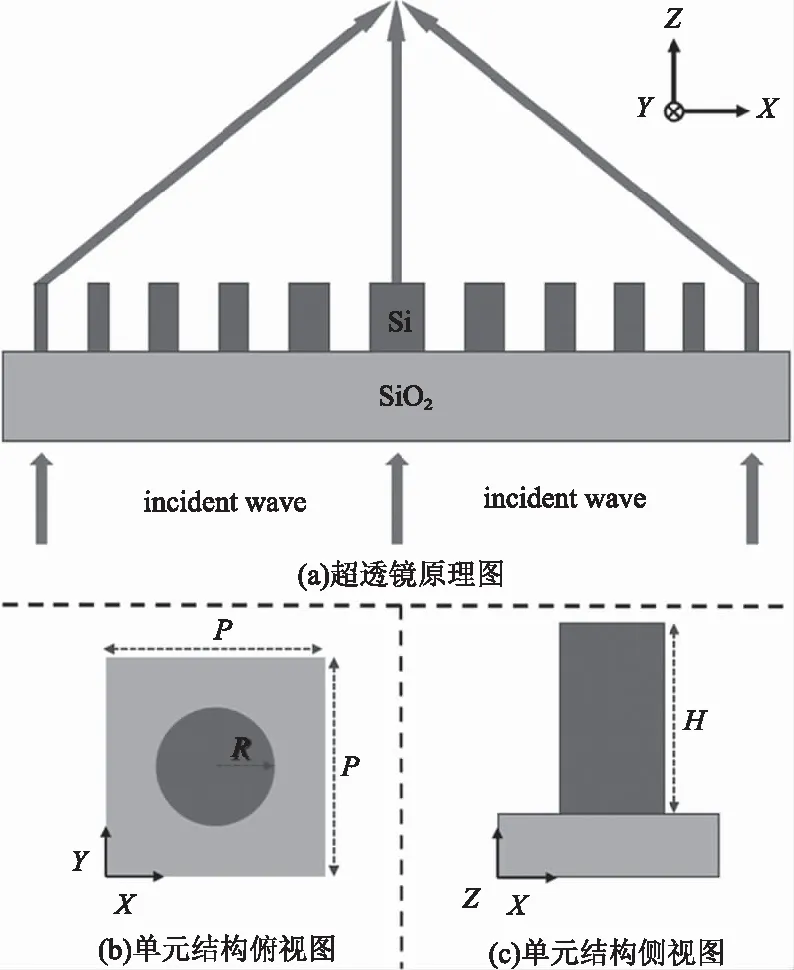
图1 超透镜工作原理图

3 仿真设计

本文以下仿真步骤和参数获取均基于加拿大公司开发的光学仿真模拟软件FDTD Solution,其分析精度高,界面美观简单,是业内公认的专业光学模拟软件。仿真分为单元结构优化和超透镜整体设计两部分。

3.1 单元结构的设计与优化

在软件中建立三维单元结构仿真模型,添加光源并设置入射平面光波长为1μm,入射方向为沿z轴正方向,偏振方向为x方向,入射角度和起始相位均设置为0,幅值为1,平面波类型选择周期波；添加网格精度为六的仿真区域并设置各边界条件,为提高仿真效率x方向选择反对称条件,y方向选择对称条件,z方向选择吸收电磁波的完美匹配层(PML);添加点监视器作为单元结构的相位监视器；添加x-y面监视器来获取透过率的数据。

首先在预定半径范围内采用固定单元结构的高度H寻找周期P的最佳值,然后利用所得最优P值重新扫描高度H,得到高度的最佳值。初始扫描时设置H=0.5λ=500 nm,半径R扫描范围35～160 nm。由奈奎斯特采样定律可知周期P需要满足下式:

(2)

其中,λ为目标波长;nsubstrate为衬底材料的折射率,故仿真周期P的扫描范围设置成350～650 nm,每25 nm取一个扫描点,共十三个扫描点。扫描所得相位变化图谱和透过率图谱如图2(a)和(b)。从相位图(a)中观察可知,H=500 nm时,在规定半径变化范围内,随着周期的增大,均能实现0～2π的全相位调控,但能实现全相位调控的有效半径范围在减小；从透过率图(b)中可以看出,在P>500 nm时会有光栅衍射级次出现外,在350 nm400 nm均可实现0～2π全相位全相位调控,但H>475 nm时存在相位不稳定越变情况,由透过率图(d)可以看出,H<425 nm时存在光栅衍射级次情况。H值越大,固定半径变化范围得情况下透镜的深宽比越高,加工难度越大,综合考虑最终选定H=450 nm。

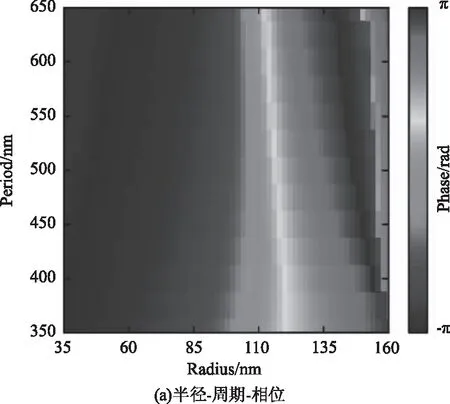
图2 相位透过率变化图

经过优化单元结构的参数变化范围如图3所示,在周期P=400 nm、高度H=450 nm,半径R=35～155 nm时就可以实现0～2π的相位变化,对应参数下的单元结构平均透过率为95.69 %,最大深宽比为6.4。

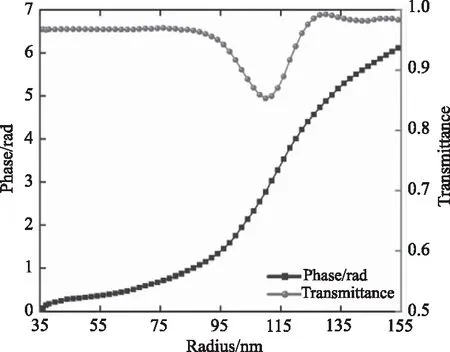
图3 单元结构优化结果

3.2 超透镜的设计与仿真

超透镜表面任意位置的相位分布函数φ(x,y)满足下式:

(3)

式中,λ表示超透镜的工作波长;f表示焦距；本次设计超透镜焦距为15 μm,透镜直径为20 μm,数值孔径0.56,通过φ(x,y)求得目标相位,再由图3中相位数据拟合出纳米柱半径与相位的关系式。在FDTD Solution中编写程序对半径不同的硅纳米柱进行排列,获得可以实现聚焦功能的超透镜模型。在衬底侧设置x方向偏振的全场散射光源沿Z轴正向射入,仿真区域边界设置xmin和ymin为PML,xmax选择对称条件,ymax选择反对称条件,z方向设置为PML。

4 讨论与分析

所设计超透镜聚焦结果如图4所示,图4(a)所示为y=0时x-z面的能流分布情况,图4(b)为沿光轴方向的能流归一化分布图,可以看到实际焦距为14.85 μm,比设计焦距相差0.15 μm,焦点偏移率为1 %。产生偏移的原因有两点:一是模拟设计超透镜相位的离散分布与理想透镜相位的连续分布；二是相邻单元结构之间存在的耦合作用。图4(c)所示为焦平面内能流分布情况,图4(d)为焦平面上y=0处沿x轴的能流归一化分布图。焦点的半高全宽FWHM为0.996 μm。

图4 超透镜聚焦场强分布图

对超透镜聚焦效率的定义为在焦平面上以焦点为中心,三倍半高全宽为直径的圆形区域内能量与总入射能量的比值,通过计算超透镜的聚焦效率为68.3 %。

本文同时研究了所设计超透镜对宽窄波段入射光的聚焦情况如图5所示,图5(a)展示了超透镜在宽波段0.9～1.1 μm工作时能流沿Z轴方向的归一化分布图,可以看出除个别低波段(0.9 μm、0.92 μm)外,其余波段均聚焦正常,并由此得到各波段的焦点位置情况如图5(b)所示。可以看出入射光波长与焦距呈负相关,且随着入射光波长的增加,焦移情况程递减趋势,焦点位置均在±2 μm内波动。图5(c)和(d)分别为超透镜在窄波段0.95～1.05 μm工作时能流分布图和焦点位置情况。显然超透镜在窄波段聚焦效果很好,焦点位置波动范围仅为±0.7 μm。

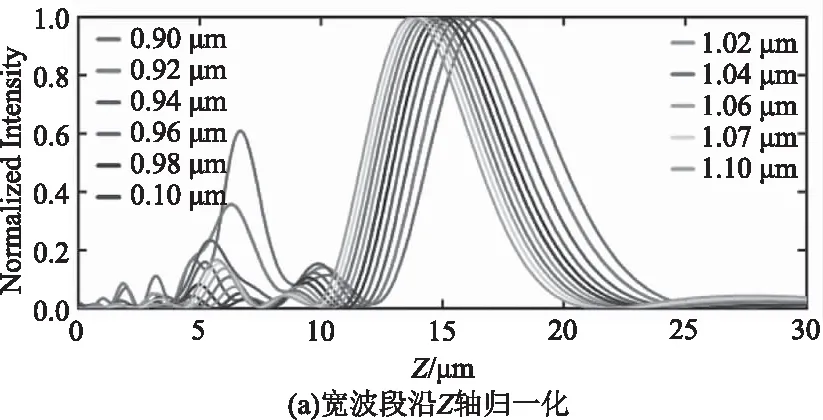
图5 超透镜在宽窄波段的聚焦特性

5 结 论

本文理论研究并数值模拟了一种硅基偏振不敏感近红外超透镜,通过对单元结构的周期P、纳米柱高度H、半径R参数的扫描优化,分析得出其对光波相位、透过率的影响并寻得最优解。工作波长为1 μm的超透镜焦距为15 μm,直径为20 μm,数值孔径(NA)为0.56,聚焦效率为68.3 %。通过对超透镜在目标波长±700 nm的色散特性研究,发现所设计透镜具有负相关散射特性,也验证在该波段范围内具有良好的聚焦效果。接下来将针对超透镜的聚焦效率、宽带消色差等问题进一步研究,为红外超透镜实现高效聚焦平面化进一步探索。