基于分数阶模型的牡蛎壳动力学特性研究*
袁良柱,陆建华,苗春贺,王鹏飞,徐松林,2
(1.中国科学技术大学中国科学院材料力学行为和设计重点实验室,安徽 合肥 230027;2.中国地震局地震预测研究所高压物理与地震科技联合实验室,北京 100036)
黏弹性材料是生活中最常见的材料之一,工业材料(塑料、橡胶、树脂、玻璃、陶瓷、混凝土等)、地质材料(岩石、土壤、沥青、石油等)、生物材料(肌肉、血液、骨骼等)常常同时具有弹性和黏性两种性质[1]。
作为一种天然复合材料,贝壳因其独特的强-弱层状结构表现出轻质高强的特性[2]。这样的结构设计也被大量应用于材料设计中,有大量工作仿照天然贝壳的结构构造,制造出了具有良好的强度、断裂韧性和冲击性能的人造仿生材料[3-5]。从结构成分上来说,贝壳由1%~5%的蛋白质和95%~99%的矿物组成,其中蛋白质的弹性模量和强度均不高(弹性模量在50~100 MPa 之间,强度仅有20 MPa),贝壳的矿物成分CaCO3的强度也不高(弹性模量在50~100 GPa 之间,而强度仅有30 MPa)[2]。但因为贝壳内部的珍珠层具有独特的多尺度、多级次的砖泥结构[5],使贝壳本身的强度能达到100~300 MPa 之间[2]。不仅如此,贝壳材料的动态力学特性同样优异。Huang 等[6]发现贝壳珍珠层在高应变率(103s-1)下的强度(500 MPa)比低应变率(10-3s-1)下的强度(200 MPa)要高得多。贝壳独特的结构特点以及其优异的力学特性引起了广泛的研究兴趣[2,6]。
贝壳因其独特的结构特征表现出相当复杂的力学特性,这种复杂材料含有大量的多尺度细微观结构,也使得材料中的应力波产生弥散和衰减现象[7-8],体现出了一定的黏弹性特性[2]。复杂材料中应力波传播有较多的研究成果[9-10],其特性均与复杂介质的细微观结构相关。Huang 等[11]研究了颗粒体系介质中分形维数与应力/破碎程度的关系,以及对局部波动效应的影响。徐松林等[7]、谭子翰等[8]基于波动方程的格林函数解,结合边界积分的方法研究了椭圆形孔洞、裂纹等细微观缺陷对波传播规律的影响。Ting 等[12]研究了周期性分层介质的波传播规律。张鸣[13]基于波传播理论,推导了梯度密度介质的波传播方程,李毅等[14-15]在此基础上,推导了梯度密度和层状介质的波传播方程,并以此分析了牡蛎壳试样的波传播规律,发现牡蛎壳试样的黏弹性会随着密度的变化而变化。这些研究所用的本构模型均是整数阶模型,在材料细微观结构的研究方面具有一定限制,无法较好反映复杂介质的细微观结构对波传播的影响规律。
传统模型如Maxwell 模型、Kelvin 模型所预测的材料松弛和蠕变过程,应力和应变满足时间的自然指数形式[16]。然而,大量的实验发现,多数黏弹性材料的松弛和蠕变过程,应力和应变往往表现为时间的幂函数形式[17]。不同于传统模型,分数阶模型的应力和应变满足时间的幂函数形式,如分数阶Kelvin 模型在蠕变下的应力应变表达式为多个幂函数之和[16]。也有学者在传统整数阶模型的基础上,通过引入多个导数项和材料参数来表征变形或应力的历史或演化,使得本构模型和实验能较好地贴合[18-23],但模型也变得更加复杂了。而与传统模型相比,分数阶模型参量少,并且能够很好地涵盖传统本构模型。例如当Abel 分数阶模型(σ(t)∝dαε(t)/dtα)中的阶数α=0 时,模型就是弹簧元件;当α=1.0 时,模型则变为牛顿黏壶元件[16]。分数阶本构关系也能更接近黏弹性的流变特性[24-25]。寇磊[26]通过矩形板蠕变的算例表明,分数阶黏弹性模型比经典黏弹性模型的适应性要好。尹耀得等[27]应用分数阶Kelvin-Voigt 模型建立了考虑记忆特征时间长度的黏弹性本构关系,对8 组不同拉伸速率下的丙烯酸弹性体单轴拉伸实验数据进行参数拟合,得到了具有高拟合决定系数的材料参数。Zhao 等[28]针对介电弹性体的黏弹性问题,建立了一种基于分数阶Kelvin-Voigt 黏弹性模型的三维本构,可被用来预测材料在自由振荡和激励振荡下的蠕变行为。牡蛎壳材料由于其内部珍珠层和粉末层两种成分的巨大差异,使得不同密度的牡蛎壳材料表现出较大的力学性能差异,并且由于其珍珠层-粉末层这种软硬交替的结构使得牡蛎壳材料表现出一定的黏弹性特性[15]。因此使用简单的整数阶模型并不能很好地表征其黏弹性特性,而分数阶黏弹性模型在复杂材料的动力学研究工作中已经取得了众多成功[29]。
本文中,首先基于时间分数阶的微积分定义,分别以Abel 模型和分数阶Maxwell 模型作为材料的本构,结合一维波传播理论得到材料的控制方程;然后利用Laplace 变换得到应力与位置坐标x、Laplace 变换参量s 的关系式,并通过数值Laplace 逆变换的方法,研究Abel 模型和分数阶Maxwell 模型中各个参数对波衰减的影响;最后,基于Abel 模型和分数阶Maxwell 模型,利用CO2脉冲激光加载技术和激光干涉测速装置,从分数阶模型参数的角度定量地分析相同加载条件下牡蛎壳试样的动力学特性与试样密度/珍珠层占比的关系。
1 牡蛎材料与CO2 脉冲激光加载技术
牡蛎壳材料具有与贝壳相似的砖泥结构特征和力学性质,由珍珠层和粉末层组成,其中的CaCO3含量在95%以上[30]。但是,牡蛎壳结构复杂,不同部位的珍珠层和粉末层含量和厚度差异大。粉末层具有多孔的细观结构特性,从放大的粉末层结构剖面中可以看到排列不规则的片状和丝状的方解石成分;珍珠层结构相对比较光滑,具有平整的纹理,放大的珍珠层结构剖面可以看到排列整齐的方解石柱。其中,珍珠母内单个文石片的平均厚度约为0.45 µm,各文石片层边沿之间间距平均约为2.35 µm,具有典型的砖泥结构特征[31]。本文中所选材料为东海出产的牡蛎壳(图1(a))。使用带有空心钻孔的电钻在牡蛎上钻下圆柱形试样,然后分别采用电磨机、砂纸逐次进行打磨。制备得到圆片形牡蛎壳试样,直径为(13.0±0.5) mm,厚度为0.4~1.0 mm(图1(a))。图1(b)为对应的牡蛎壳试样纵剖面的扫描电镜(scanning electron microscope,SEM)照片。

图1 牡蛎壳材料、圆形实验试样、试样纵剖面电镜照片与局部放大Fig.1 Oyster shell material, circular sample, longitudinal section electron microscopy (SEM) and local magnification
由于制备的牡蛎壳试样密度分布变异性很大,采用常规SHPB 装置中直径较大的入射杆进行实验(即便采用4~6 mm 直径的入射杆)不能很好地反映牡蛎壳试样结构的局部动态力学性能。因此,本文中应用CO2脉冲激光加载技术,将其光斑聚集到直径1 mm,对牡蛎壳试样进行加载,结合激光干涉测速(laser interferometer velocimetry system,VISAR)装置进行自由表面粒子速度波形的测量。
图2 为CO2脉冲激光对贝壳试样进行冲击加载及速度信号采集的示意图。实验中,在试样冲击面放置光电传感器作为实验信号的触发源,在试样的另一面放置VISAR 系统中的光纤探头(光纤探头与试样贴近但不接触),VISAR 系统中的光纤探头可以发射测速激光并收集试样表面反射回的激光信号,反射光信号通过与VISAR 系统相连的示波器采集,利用反射光信号,就可以分析得到试样表面的粒子速度。实验时,由CO2脉冲激光器发射一束激光,经凸透镜会聚后冲击牡蛎壳试样。当激光冲击试样时,试样前表面的光电传感器触发信号,光纤探头连接的VISAR 系统开始采集牡蛎壳试样表面的信号。通过改变透镜与试样之间的距离,可以调整激光光斑的大小与能量密度,以此来调整冲击加载的强弱。本文中所有实验试样与透镜的距离均相同,并且激光冲击试样的区域也相同,以此来达到控制相同密度试样相同加载的条件。

图2 CO2 脉冲加载与激光干涉测速系统(VISAR)Fig.2 CO2 pulse loading and laser interferometer velocimetry system (VISAR)
由于牡蛎壳试样的密度可以反映所含珍珠层的占比,取密度为0.5、0.7、1.2 和1.4 g/cm3共4 种牡蛎壳试样进行实验,以此来探讨不同珍珠层占比对牡蛎壳试样黏弹性的影响。
由于牡蛎贝壳类材料内部的砖泥结构使其表现出微观异构、宏观连续的特征,传统的整数阶微分本构模型不能很好地描述它们的力学行为,而时间分数阶导数可以更加准确地体现复杂材料的力学行为[16]。因此,下面将结合分数阶导数的定义,推导得到应用分数阶模型的动力学控制方程及其应力解,基于此,结合激光冲击实验来研究牡蛎材料的动力学特性。
2 时间分数阶本构模型及动力学控制方程
2.1 时间分数阶微积分与黏弹性模型
从分数阶导数被提出以来,不断有学者从不同的角度出发提出几种分数阶微积分定义。其中,Riemann-Liouville、Caputo、Grünwald-Letnikov 和Riesz 定义在基础数学和工程应用中比较常用。Grünwald-Letnikov 定义主要用于数值计算中差分格式的计算;Riesz 定义是关于空间分数阶的定义。Riemann-Liouville 定义和Caputo 定义均是基于多重积分思想的定义,Riemann-Liouville 型分数阶导数在数学理论分析中较常用,但具有超奇异性;而Caputo 定义具有弱奇异性,更适合地球物理建模。因此本文将采用Caputo 定义的分数阶微分定义来描述黏弹性材料的应力应变行为。
对于任意实数α>0,Riemann-Liouville 分数阶积分定义[16,32]:

在式(1)的基础上,Riemann-Liouville 型分数阶微分定义为:

Riemann-Liouville 型微分定义是先求积分再求微分,与此相反,Caputo 型微分定义是先求微分再求积分,其表达式[16]为:

将分数阶时间导数应用于分析黏弹性材料的力学行为,目前主要是将传统模型中的牛顿黏壶替换为Abel 黏壶。Abel 黏壶模型示意图如图3(a)所示,本构关系为:

图3 几种分数阶本构模型Fig.3 Several fractional differential constitutive models

式中:σ(t)为模型整体受到的应力;ε(t)为模型整体的应变;η 为Abel 黏壶的黏性系数,其量纲随着分数阶阶数α 的变化而变化,单位可写为Pa·sα[28]。可以发现,当α=0,Abel 黏壶变为弹簧元件,代表弹性固体;当α=1.0 时,Abel 黏壶变为牛顿黏壶,代表牛顿流体。
分数阶Maxwell 模型由1 个弹簧元件和1 个Abel 黏壶串联而成。模型示意图如图3(b)所示,本构关系为:

式中:E 为模型中弹簧元件的弹性模量。
特别地,当初始条件满足σ(t)|t=0=0、ε(t)|t=0=0 时,则Abel 黏壶和分数阶Maxwell 模型的Laplace 变换分别为:

2.2 基于分数阶本构模型的动力学控制方程求解
对于一个半无限长的复杂介质(内部含有孔洞、间隙、界面等细微观结构),应用时间分数阶本构模型(以Abel 黏壶为例),则一维应变下的控制方程组为:

式中:σ、ε、v 分别为单元体的应力、应变和速度,x 为Euler 坐标系下的坐标,t 为时间,ρ 为材料密度,α、η 为Abel 黏壶的分数阶阶数和黏性系数。
当初始条件满足σ(t)|t=0=0、ε(t)|t=0=0 时,应用式(6a),并对式(7)进行Laplace 变换,整理得到:

可以发现,式(8)满足Euler 方程的形式,求解得到其解析解为:

式中:A(s)为经过Laplace 变换的积分常量。
同理,可以得到分数阶Maxwell 模型下控制方程的应力解为:

式中:E 为模型中弹簧元件的弹性模量,B(s)为经过Laplace 变换的积分常量。
对于式(9)~(10)中的Lapalce 积分常量A(s)、B(s),可以通过x=0 处的边界条件得到。以式(9)为例,假定一个函数p(t)作为x=0 处的边界条件,通过Laplace 变换将p(t)转变为P(s),最后代入式(9)得到:

将式(11)代回式(9),得到:

同理,利用边界条件,由式(10)也可以得到:

为简化问题,以图4 所示的单个半脉宽正弦函数作为x=0 处的边界条件,其相应的Laplace 变换式为:

图4 单个半脉宽正弦函数Fig.4 Single half pulse width sine function

式中:A0和w0分别为正弦函数的幅值和频率,u(t)为单位阶跃函数,图中T=2π/w0为正弦函数的周期。

同样,以Abel 黏壶模型为例。假定材料密度ρ 为1 000 kg/m3,分数阶导数阶数α 为0.5,η 为1 MPa·s0.5。若输入正弦信号的幅值和脉宽分别为100 MPa 和100 µs,可得到波传播到各个位置处的波形,如图5(a)所示。可以发现,随着传播距离的增大,波的幅值逐渐减小,体现出了分数阶模型的黏弹性特性。从图5(b)可以看出,正弦波传播到x=20 mm 处的波形脉宽远远大于100 µs,相比加载的时间,波形卸载的时间要远比入射波长,这同样体现了分数阶模型的黏弹性特性。

图5 正弦波在Abel 黏壶模型介质的衰减Fig.5 Attenuation of a single half pulse width sine wave in Abel model media
2.3 分数阶模型参数敏感性分析
对于Abel 黏壶而言,当α=0 时,σ=ηε=ηΔl/l,此时应力与介质的变形量Δl 有关,反映出模型的弹性特性;当α=1.0 时,σ=ηdε/dt=ηv/l,此时应力与介质的速度v 有关,反映出模型的黏性特性;当α=2.0 时,σ=ηd2ε/dt2=ηa/l,此时应力与介质的加速度a 有关,可以认为模型此时反映的是介质的惯性特性。若介质是完全弹性的(α=0),系数η 为弹性模量,此时波传播不会产生衰减;若介质是黏性的(α=1.0),系数η 为黏性系数,此时波传播会产生衰减。那么当介质是惯性(α=2.0)的时,其波传播同弹性介质和黏性介质会有什么区别?
当α 分别为0、1.0 和2.0 时,式(12)变为:


以图4 所示的正弦波为输入信号,分别计算了阶数α 为1.0 和2.0 时,波传播在各个系数η 下的波形,如图6(a)所示。当α=1.0、η=1 kPa·s 时,波产生了衰减,并且波的脉宽变得很长,表现出明显的黏弹性特征。随着系数η 的上升,波的脉宽逐渐接近输入信号的脉宽(100 µs),并且波的衰减也很小,说明介质黏性(α=1.0)对波的衰减和波长均会产生影响。从图6(b)可以看出,当α=2.0、η=1 kPa·s2或η=1 MPa·s2时,波也会产生衰减,但衰减的程度很小,波形和α=1.0、η=1 MPa·s 的形状相似,说明这两种情况对波衰减的作用相近。虽然当α=2.0、η=0.1 Pa·s2时,得到的波形的幅值与α=1.0、η=1 kPa·s 的相近,但脉宽或者说波长相差甚大,十分接近输入信号的脉宽(100 µs)。这体现了惯性特性与黏性特性的不同之处,即介质的黏性会使波的幅值和波长均改变,而惯性特性仅仅改变波的幅值。

图6 当α 分别为1.0 和2.0 时的波传播特性Fig.6 The property of wave propagation when the order α is 1.0 and 2.0 , respectively
为了进一步探究阶数α 和系数η 的取值对波传播的影响,仍以图4 所示的正弦波为输入信号,分别以 Abel 模型和分数阶Maxwell 模型作为材料本构,讨论其中的参数对波传播幅值衰减的影响。
假定材料密度ρ 为1 000 kg/m3,α 从0 变化到1.4,设η 为1、2 和3 MPa·sα等3 种情况。若输入信号的幅值和脉宽分别为100 MPa 和100 µs,可得到其传播至x=10 mm 处的应力波幅值与α、η 之间的关系,如图7(a)所示。

图7 参数α、η 和E 对幅值衰减的影响Fig.7 Influence of parameters α, η and E on amplitude attenuation
从图7(a)可以看出,在η 不变的情况下,应力波的幅值衰减程度随着阶数α 的增大呈现出非单调的变化,α 存在一个中间值,能使波的衰减达到最大。此外,当阶数α 不变时,η 越大,波的幅值衰减程度越小。
与Abel 黏壶模型相比,分数阶Maxwell 模型更加多样化,与控制方程联立得到的应力解形式也更加复杂。分数阶Maxwell 模型含有3 个参数:弹簧弹性模量E、黏性系数η 和分数阶阶数α。同样设定材料密度ρ 为1 000 kg/m3,α 从0 变到1.4;在E 值(10 GPa)不变时,取η 为1、2 和3 MPa·sα等3 种值;在η 值(1 kPa·sα)相对较小时,取E 为1、5、10 和100 GPa。若输入正弦波信号的幅值和脉宽分别为100 MPa 和100 µs,可得到传播至x=10 mm 处的应力波幅值与α 之间的关系如图7(b)和图7(c)所示。
从图7(b)可以看出,对于分数阶Maxwell 模型,阶数α 和黏性系数η 对幅值衰减的影响同Abel 黏壶相同。从图7(c)可以看出,在黏性系数η 相对较小时,E 对波衰减的影响很小。因此,可以认为,应力波的衰减主要由分数阶Maxwell 模型中的Abel 黏壶控制。
3 冲击下牡蛎材料的黏弹性特性
3.1 牡蛎材料在激光冲击下的力学特性
图8 所示为不同密度、不同厚度的牡蛎壳试样在脉冲激光冲击下的速度时间信号,从图中可以看出,输出信号的幅值随着试样厚度的增大而变小,这反映了牡蛎壳试样的黏弹性特性。比较特别的是:通过对不同密度牡蛎壳试样的输出信号进行比较,发现试样密度越大,其粒子速度的幅值衰减得也越大。这与一般认为的密度越大、材料黏弹性越小相反。其原因在于:CO2激光脉冲器发射的激光波长约为1.064 µm,产生的冲击脉冲宽度为几个微米,这与珍珠层中文石片边沿的平均间距(2.35 µm)比较接近,即与砖泥结构间的缝隙尺寸相近,使得激光脉冲在珍珠层中发生较大的散射,产生更大的能量损耗。此外,由于牡蛎材料具有较复杂的层状结构的特征,局部存在一定的交互层错结构。当存在这种交互层错结构时,由激光脉冲激发的短脉冲波就会在局部产生反射波和透射波,这些复杂波系的相互作用,会使速度信号产生局部的极值。

图8 各个密度下不同厚度牡蛎试样的速度信号及拟合曲线Fig.8 Velocity signals and fitting curves of oyster samples with different thicknesses and densities
3.2 牡蛎材料的分数阶模型参数拟合方法
由于激光干涉测速系统只能测得牡蛎壳试样背面的速度信号(即输出信号)。对于冲击信号(即输入信号),无法得到其具体数值。因此下面将基于输出信号,推导在CO2激光加载实验中获取牡蛎壳试样分数阶黏弹性参数的方法。

利用式(22) 等号右边和拟合得到的相同密度、不同厚度牡蛎壳试样的速度时间曲线,用数值Laplace 进行计算得到一组数据后,再用式(22)等式左边(即ρtα+1/[ηΓ(α+2)])对其进行拟合可得到对应密度牡蛎壳试样的Abel 黏壶模型参数α 和η。
同理,可以得到分数阶Maxwell 模型参数的拟合式为:

与获取Abel 黏壶模型参数的过程相同,同样可以得到分数阶Maxwell 模型参数α、η 和E。此外,拟合得到的参数中,分数阶阶数0<α<2.0,其中的整数0、1.0 和2.0 分别对应了材料的弹性、黏性和惯性。黏性系数η 和弹性模量E 为大于0 的实数,弹性模量E 应与材料的杨氏模量量级相当。
值得注意的是,由于式(22)~(23)中含有1/(hk-hkʹ)2项,因此需要选择相近密度下厚度不同的牡蛎壳试样的速度信号进行分数阶模型参数的拟合。并且为了统一实验信号的拟合条件,设定信号范围从0 开始,至峰值点结束,且同一密度的牡蛎壳试样的实验信号的时间范围均取一致。图8 所示的不同密度、不同厚度牡蛎壳试样的输出速度信号,其形状类似正弦形,因此,类比式(12)~(13)的结果,在单个正弦函数的基础上乘上时间衰减项ebt,即:

式中:Δt=Δx/c=(hkˊ-hk)/c 为波在厚度分别为hkˊ和hk的牡蛎壳试样中传播的时间差,c 为波速。根据李毅[15]对牡蛎壳试样的研究,c 可取为(0.369 m4·s-1·kg-1) ρ + 1 744 m·s-1。
3.3 牡蛎材料的分数阶模型参数及黏弹性分析
通过3.2 节的拟合方法,应用式(26)对0.5、0.7、1.2 和1.4 g/cm3密度的牡蛎壳试样分别进行Abel 黏壶模型和分数阶Maxwell 模型的参数拟合,记式(26)中等号右侧为aL,单位为s3/m2。
图9(a)~(b)所示为不同密度牡蛎壳试样对应曲线的拟合情况,曲线拟合的结果良好。表1 给出了各密度牡蛎壳试样的Abel 黏壶模型和分数阶Maxwell 模型的拟合参数值。对于0.5 和0.7 g/cm3等较低密度的牡蛎壳试样,拟合得到的分数阶阶数小于1.0,此时材料的性质表现为黏弹性特性;对于1.2 和1.4 g/cm3等密度较高的牡蛎壳试样,拟合得到的分数阶阶数大于1.0,此时材料的性质逐渐向惯性靠拢。
分数阶阶数、黏性系数随密度变化的趋势如图9(c)所示,阶数与密度的关系近似呈线性关系,而黏性系数与密度的关系近似呈指数衰减关系。牡蛎壳试样的珍珠层占比与试样的密度是成正比的,这说明拟合得到的阶数α 可以侧面反映牡蛎壳试样的结构特性。
由于不同密度试样对应的分数阶阶数和黏性系数均不同,无法对不同密度的牡蛎壳试样的黏弹性进行定量的比较。因此固定分数阶阶数α,对不同密度的牡蛎壳试样的黏弹性参数进行拟合。固定的分数阶阶数α 取为表1 中4 种密度试样拟合得到的α 平均值。对于Abel 黏壶模型来说,固定的分数阶阶数为1.0;对于分数阶Maxwell 模型来说,其值为0.94。当α=1.0 时,Abel 黏壶模型变为牛顿黏壶模型,此时模型没有了弹性部分,因此对此种情形不进行拟合。当α=0.94 时,用分数阶Maxwell 模型得到拟合的结果如图9(d)中所示,对应的拟合参数如表2 所示。

表1 牡蛎壳试样分数阶模型的拟合参数Table1 Fitting parameters of the fractional model of the oyster sample

表2 固定分数阶阶数情况下,牡蛎壳试样分数阶Maxwell 模型的拟合参数Table2 Fitting parameters of fractional Maxwell model for oyster shell samples in the case of fixed fractional order
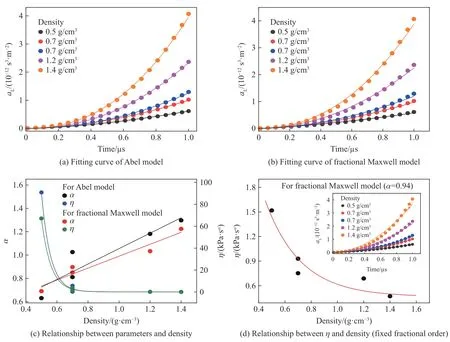
图9 牡蛎试样分数阶模型的拟合曲线及参数与牡蛎试样密度的关系Fig.9 The fitting curve of the fractional model of the oyster sample and relationship between parameters and oyster sample density
可以看出,在固定分数阶阶数的情况下,随着牡蛎壳试样的密度的增大,分数阶模型的黏性系数在减小,试样的黏性在增大。并且黏性系数与试样密度的关系并不是线性关系,而是近似呈现指数衰减关系,在牡蛎壳试样的密度达到1.2~1.6 g/cm3时,黏性系数的数值趋于平稳。这进一步说明,牡蛎壳试样的密度越大,或者说牡蛎壳试样中珍珠层的占比越高,试样的黏性越大;但当密度达到一定数值后,或者说珍珠层占比达到一定值后,珍珠层占比的增加对波衰减的提升将不再显著。这对复合材料的结构设计具有一定的指导意义。
4 结 论
本文中从波传播理论出发,基于Caputo 分数阶微分的定义,以Abel 黏壶模型和分数阶Maxwell 模型作为材料本构,得到了相应的波传播控制方程,通过Laplace 变换得到了控制方程的解析解。结合解析解,通过Laplace 数值逆变换分别分析了Abel 黏壶模型和分数阶Maxwell 模型中分数阶阶数α、黏性系数η 及弹性模量E 对波衰减的贡献;结合CO2脉冲激光实验测试信号给出了拟合分数阶本构模型参数的方法。在相同的加载条件下,分别得到了4 种密度(0.5、0.7、1.2 和1.4 g/cm3)的牡蛎壳试样的分数阶模型参数。得到的主要结论如下。
(1) Abel 模型和分数阶Maxwell 模型中分数阶阶数α 和黏性系数η 对应力波的衰减均有贡献,而弹性模量E 对波衰减的影响很小。波的衰减并不随着阶数α 的增大而单调变化,α 存在一个中间值,能使波的衰减达到最大。特别地,当α=2.0 时,波传播表现出幅值衰减、形状不变的特征。
(2)在相同的加载条件下,牡蛎壳试样的密度越大,或者说牡蛎壳试样中珍珠层的占比越高,试样的黏性越大。这是由于CO2激光脉冲器发射的激光波长与牡蛎壳试样珍珠层的砖泥结构间的缝隙尺寸相近,使得激光在冲击牡蛎壳试样中的珍珠层时发生较大的散射。
(3)在不固定阶数α 的情况下,拟合得到的阶数α 反映出牡蛎壳试样随着密度的增大由黏弹性机制向惯性转变的趋势。在固定阶数α 的情况下,随着牡蛎壳试样密度的增大,分数阶模型的黏性系数η 减小,但关系并不是线性的,而是近似为指数衰减。这说明当密度达到一定数值后,或者说珍珠层占比达到一定阈值后,珍珠层占比的增加对波衰减的提升将不再显著。

