钢箱梁悬索桥风致响应与静力分析

文海泉，马小淇，江阿兰

(大连交通大学土木工程学院，辽宁 大连 116622)

现代桥梁不断朝着大跨度和轻质量的方向快速发展，导致桥梁结构刚度和阻尼不断降低，从而大大增加了结构对风荷载的敏感性。钢箱梁悬索桥同时具备这两样优点，如今在跨江大桥中得到广泛应用，随之而来我们更需要考虑风荷载对桥梁的影响，风荷载已经成为悬索桥结构设计和施工的主要控制荷载[1-2]。

风经过桥梁结构时，会将风的动能转化为桥梁的能量，造成了桥梁振动，反之，振动起来的桥梁又会影响空气的流动，改变空气作用力，形成了风与结构的相互作用。例如，1940年美国塔科马大桥设计不当发生颤振，2020年虎门大桥因连续设置水马，改变了钢箱梁的气动外形，引起了涡振现象。主梁的选型与尺寸，整体桥梁的跨度都对桥梁抗风性能有着至关重要的影响。

以某座钢箱梁悬索桥为例，采用有限元软件对主梁进行数值风洞模拟，分析桥梁风致响应情况，对整桥进行静力分析，验证桥梁的安全性。

1 桥梁模型

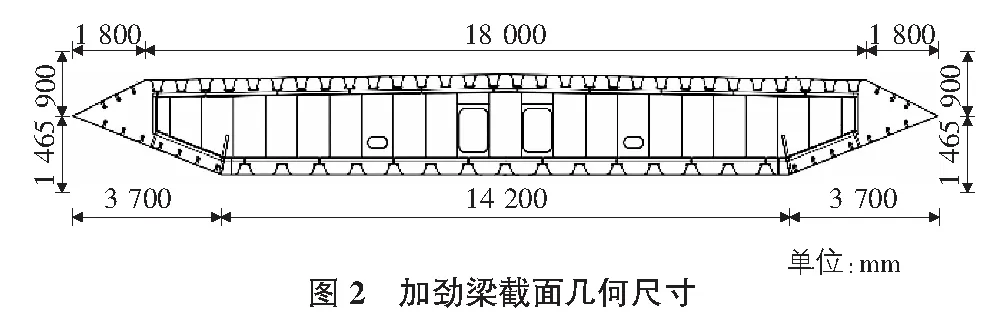
桥梁模型为(125+405+125)m地锚式两塔连续钢箱梁悬索桥。加劲梁共有两对竖向支座，设于两个锚碇上。主缆中跨矢跨比为1/10.5，主梁中心距为19 m，加劲梁是闭口扁平流线型钢箱梁，高2.5 m，宽21.6 m(含风嘴)。桥梁总体布置和加劲梁断面尺寸见图1，图2。

主缆和吊索设置为节点有三个线自由度的索单元，用于模拟仅能受拉的杆件。主缆锚固处和索塔底为固结；主缆在塔顶主鞍中心处按永不脱离点考虑；加劲梁梁端约束竖向、横桥向的位移和绕X轴(顺桥向)的转动；约束索塔下加劲梁横桥向的位移。

2 静力三分力

平均风对桥梁作用力称为静力三分力，按照体轴坐标，体轴系分为阻力系数FH、升力系数FV、扭矩系数FM三个分量，按照风轴坐标，风轴系分为阻力系数FD、升力系数FL、扭矩系数MT三个分量。

风轴坐标下的静力三分力系数可表示为[3]：

阻力系数：

(1)

升力系数：

(2)

扭矩系数：

(3)

其中，U为断面来流平均风速；ρ为空气密度；D，B分别为桥梁断面的高度和宽度。

风轴坐标系和体轴坐标系下的三分力系数存在如下换算关系，转换式如式(4)所示，示意图如图3所示。

(4)

2.1 计算模型

采用有限元软件建立二维流场，模型尺寸大小与实际相同，为了提高计算效率，对路灯、栏杆等进行忽略处理[4]。计算区域为95 m×35 m，流场几何尺寸见图4。

2.2 网格划分

将流场分为5个区域进行网格划分，对桥梁截面周围进行网格加密，网格尺寸取0.02 m，同时也为了平衡计算精度和计算速率，离截面较远的流场区域，受到截面的干扰小，网格尺寸取0.1 m，在上下两端的边缘区域尺寸取0.4 m。0°攻角下流场的网格划分如图5所示。

2.3 CFD边界条件

流场的湍流模型采用大涡模拟湍流模型，桥梁截面壁面函数选取无滑移壁面函数，流场上下端选取滑移壁面函数[5]，线入口风速设置10 m/s，线出口压强为0，对应计算模型的雷诺数为1.61×106，湍流动能0.107 8 m2/s2，湍流长度尺寸为0.175 m，湍流黏度比为2.08×103，其他参数均采用默认设置。流场材料选用空气，定义密度为ρ=1.184 5 kg/m3，黏度为μ=1.844 4×105kg/(m·s)。亚松弛因子等计算参数均采用默认值，时间增量0.005 s，步骤数30 000。

流场边界条件设置如图6所示。

2.4 静力三分力计算结果

静力三分力系数能够反映桥梁在静风作用下三个分量的受力与截面的关系，体现截面在风荷载作用下的气动性能。CFD模拟主梁断面-12°～+12°的三分力系数汇总图见图7(a),图7(b)。

根据风轴和体轴的坐标系图，看到钢箱梁的静力三分力系数数值变化较为平滑，没有出现数值骤变情况。主梁设计阻力系数在0攻角时最小，说明此时主梁受到的风荷载阻力最小，角度越大受到的阻力越大；升力系数随攻角增大逐步上升，风荷载对桥梁的升力作用由向下到向上；扭转系数增大幅度并不明显，可以推测主梁在风荷载作用下扭转可能性不大。

3 桥梁风致响应分析

3.1 桥梁结构动力特性

为了保证桥梁结构的稳定性与安全性，我们需要确定结构的动力反应分析，即结构频率、自振周期等，为分析结构性能提供依据[6]。

采用多重Ritz向量法进行结构动力特性求解，表1为桥梁前五阶基频、周期、振型及振型特点。

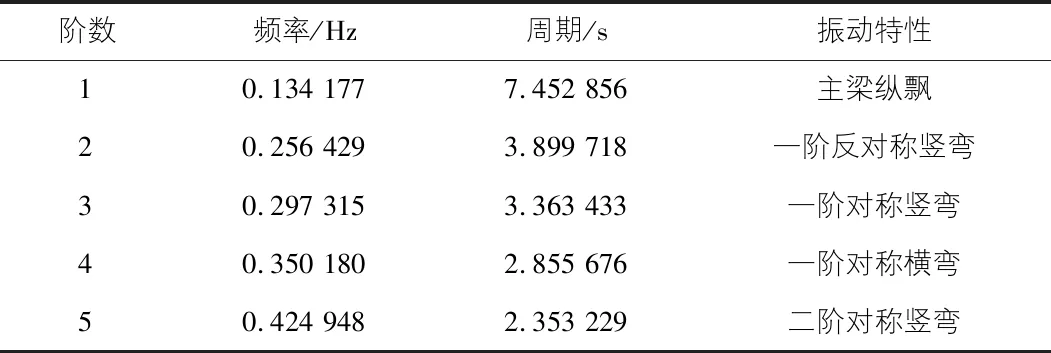
表1 结构动力特性

3.2 驰振稳定性分析

驰振是桥梁在运动中不断吸收能量，产生负阻尼使加劲梁振动逐渐增大，发生空气动力失稳的一种现象[7]。根据Den Hartog驰振理论，桥梁阻尼项的正负决定结构振动是否稳定，当气动力引起的负阻尼大于结构自身阻尼才会导致结构的驰振发散。本文模型采用混凝土桥塔，阻尼较大，只需要对钢箱梁进行验证。公式为：

(5)

(6)

(7)

其中，Cg为结构断面驰振力系数，用于判断驰振稳定性。

代入桥梁断面静力三分力系数，可知宽高比大于4，驰振力系数大于0，力的变化与速度方向相同，不会产生负阻尼，桥梁驰振稳定性良好，与桥梁结构动力特性扭转振型靠后情况相符。

3.3 颤振稳定性分析

颤振稳定性If反映了颤振稳定性能要求与桥梁颤振稳定性的关系，可以通过该系数判别桥梁颤振综合性能[8]，按下式计算：

(8)

(9)

其中，Ks因闭口箱梁取12;μ为桥梁结构与空气密度比，经计算μ=176.5;Ud=50.1 m/s;ft为主梁梁扭转基频，取主梁的扭转基频0.742;B=21.6 m;ρ=1.184 5 kg/m3;b为主梁特征长度,为10.8 m。

If计算得2.8，因为2≤If<4，根据规范桥梁的颤振临界风速Uf按下式计算：

Uf=ηsηαUco

(10)

(11)

其中，ηs为形状系数,取0.7;ηα为攻角效应系数,取0.8;Uco为与主梁相同宽度的理想平板颤振临界风速;r为桥梁惯性半径,为1.05;b=10.8 m;ft=0.742。

主梁颤振检验风速为：

Ucr=kμfUd2

(12)

其中，k为考虑风洞试验误差及设计、施工中不确定因素的综合安全系数,取1.2；μf为考虑风速的脉动影响及水平相关特性的无量纲修正系数,取1.24。

Uf=92.8 m/s≥Ucr=74.6 m/s，所以本桥发生颤振的可能性很小，满足颤振稳定性要求。

3.4 涡振稳定性分析

涡激振动发生时，结构的振动将对漩涡的脱落产生反馈作用，使涡脱频率在相当长的风速范围内被结构自振频率所俘获，这种现象被称为“锁定”，这段风速范围被称为“锁定风速区间”，在锁定风速区间内，涡振振幅先增加后减小，存在一个极大值(见图8)。

先计算加劲梁断面的斯特罗哈尔数St，由下式计算：

(13)

其中，fs为涡流脱落频率，由升力系数卓越频率经傅里叶变换得到;D为桥梁断面的高度;V为来流平均风速。

再计算涡激共振发生风速：

(14)

其中，fn为弯曲或扭转振动频率，取动力特性竖弯振型频率。

将升力系数卓越频率的傅里叶变换，在30 m/s风速下涡流脱落频率为3.52，斯特劳哈尔数为0.283(见图9)。

采用CFD软件对桥梁截面进行涡振分析，在-6°～+6°攻角范围内出现涡旋脱落时，最大振幅为0.06 m，对桥梁整体安全性影响不大，同时由于桥梁跨度不大且风作用对桥梁影响较小 ，可以认为该桥在自然风作用下不会发生较大的涡振振幅(见图10)。

根据静力三分力系数对钢箱梁进行驰振、颤振与涡振分析，判断出本桥主梁风致响应情况较好，不会出现明显的风致振动。

4 桥梁结构静力分析

4.1 桥梁风环境

W1和W2两个风作用水平对应的风速分别为重现期10 a与重现期100 a对应的风速值[9-10]。W1风作用水平体现了频遇荷载的概念，当风荷载与汽车荷载及相关荷载作用组合时，风荷载按W1风作用水平确定；在W2风作用水平下进行相关极限状态设计时，汽车荷载不参与荷载组合。

在weather spark上查得该地区地面以上10 m高，频率分别为1/10和1/100平均年最大风速，按最大风速服从极值Ⅰ型分布，可得10 a的10 min平均年最大风速期望值为U110=24.31 m/s，100 a最大风速期望值U210=29.18 m/s。

桥梁位于入海口，地表粗糙度类型按Ⅰ类场地计算。主梁构件高度高出水面37 m，所以桥梁设计基准风速可按下式计算：

Ud1=kfktkhU110=34.22 m/s

(15)

Ud2=kfktkhU210=43.07 m/s

(16)

其中，kf为抗风风险系数,取值1.02；kt为地形条件系数,取值1.0；kh为地表类别转换及风速高度修正系数,取值1.38。

根据抗风设计规范，当W1风作用在主梁上的风速值大于25 m/s时，取Ud1=25 m/s；W2风作用风速取Ud2=43.07 m/s。

4.2 W2风作用下等效静阵风荷载

如今在工程实例中一般将风荷载等效成静力作用进行分析，本文将风对加劲梁和桥塔的作用以梁单元荷载施加到结构上，对主缆和吊索的作用以节点荷载施加到单元两端。

W2风作用下主梁等效静阵风风速Ug2可表示为：

Ug2=GVUd2

(17)

其中，GV为等效静阵风系数，按照规范取值1.22。

加劲梁上单位长度等效静阵风荷载按下式计算[11]：

(18)

(19)

(20)

其中，主梁的静气动力系数CH,CV,CM选用-3°～+3°范围内的最不利值;ρ为空气密度；D,B分别为桥梁断面的高度和宽度。

作用桥塔、主缆、吊索的横桥向等效静阵风荷载只需要计算风荷载引起的阻力，按下列公式计算：

(21)

Ug=GVUd

(22)

其中，桥塔的风速按0.65塔高处风速计算，GV为等效静阵风系数;CD为各构件阻力系数;An为构件单位上顺风向的投影面积，都按规范取值。

4.3 W1风作用下等效静阵风荷载、温度荷载、汽车与人群荷载

W1风作用下主梁等效静阵风风速Ug1可表示为：

Ug1=GVUd1

(23)

作用在加劲梁、桥塔、主缆、吊索的风荷载都按式(18)～式(21)计算。

风灾是自然灾害中发生最频繁的灾害之一，但桥梁在正常使用阶段，不仅仅要考虑风荷载的影响，同时温度荷载与车道荷载也是常见荷载，需要考虑不同荷载组合的工况。

温度荷载按体系升温(钢结构升温20.9 ℃，混凝土索塔升温14.4 ℃)；体系降温(钢结构降温-20.8 ℃，混凝土索塔降温-11 ℃)。

汽车荷载采用公路—Ⅰ级车道荷载，按照规范换算成均布荷载，横向4个车道，横向车道布载系数为0.67，纵向折减系数为0.96，普通车换算集度为27.09 kN/m，重车换算集度为43.12 kN/m。当W1风荷载与汽车荷载组合时，作用在汽车上的横向风荷载增加值取为1.5 kN/m。

人群荷载集度为12 kN/m(两侧)。

4.4 计算结果分析

为了分析不同的荷载工况对桥梁的影响，将荷载工况分为以下三种：①工况1：升温荷载；②工况二：升温荷载+W2风荷载；③工况三：升温荷载+W1风荷载+车道荷载。

通过分析表2～表5的数值模拟结果得出结论。

表2 加劲梁与塔顶位移 cm

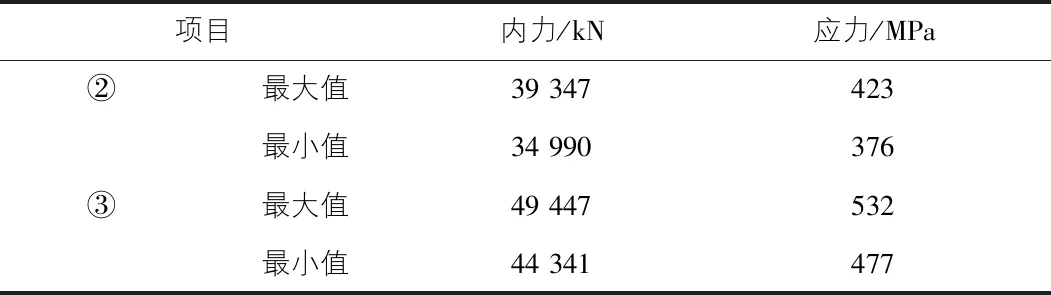
表3 主缆内力及应力表

表4 桥塔内力表(轴力受压为正)

表5 加劲梁内力表(轴力受压为正)

1)荷载工况①中升温作用下加劲梁最大纵向位移为8.17 cm，最大竖向位移向下且为31.89 cm，如图11(a)所示，温度对钢箱梁悬索桥变形的影响需要重点考虑。

2)荷载工况②中，W2风荷载作用桥梁产生最大横向位移在跨中14.10 cm，如图11(b)所示，横向位移挠跨比1/155满足规范要求最大横向位移挠跨比。

3)荷载工况③中，荷载组合引起的最大竖向位移为149.10 cm，如图11(c)所示，竖向位移挠跨比为1/300,大于规范要求的1/250。

整理上表不同荷载工况下的主缆、桥塔与加劲梁位移与内力，温度荷载对桥梁竖向位移影响较大，W2风荷载对桥梁横向有较大影响，W1风荷载与车辆荷载工况下产生对桥梁最大的竖向位移。

5 结论

本文通过某座钢箱梁悬索桥为计算模型，通过CFD软件求出主梁断面的静力三分力，并对桥梁结构进行风致响应分析与结构静力分析，得出以下主要结论：

1)对桥梁截面进行二维CFD分析，得到主梁断面-12°～+12°的三分力系数，根据数据可知该桥梁截面的气动性能较好，为接下来分析桥梁风致响应有数据支撑和可预见性的帮助。2)在桥梁风致响应分析中，驰振、颤振与涡振均满足规范要求，主梁抗风动力性能良好，发生风致振动可能性较低，符合关于静力三分力数值的预测。3)温度荷载、风荷载与车道荷载对桥梁结构都造成了明显的横向位移或竖向位移，所以钢箱梁悬索桥因为跨度大、刚度小的原因，更需要在设计阶段和施工阶段考虑桥梁这些荷载的影响，满足结构性能需求和使用要求。