峰值速度和峰值位移对6 层钢结构弹塑性地震反应影响的研究1
王 飞 张郁山 尤红兵 赵凤新
1)北京市地震局, 北京 100080
2)中国地震灾害防御中心, 北京100029
引言
地震动本身是一个复杂的随机过程,在诸多因素的影响下,实际的地震动记录具有较强的随机性(杨溥等,2000;王国新等,2008;Katsanos 等,2010),包含了不同的地震动峰值加速度、峰值速度、峰值位移、频谱特性以及地震动持时等多种信息。地震动的三要素包括地震动峰值、频谱特性和持时,这3 个要素对结构地震反应起着决定性的影响作用(Chopra,2001;胡聿贤,2006)。关于地震动峰值特性,以往的认识主要集中在对于峰值加速度的研究上,然而峰值特性不仅包括峰值加速度,还包括峰值速度和峰值位移。近年来对峰值速度和峰值位移的研究逐渐引起重视(张斌等,2021)。
对于峰值速度的研究主要集中在近断层速度脉冲方面。Bertero 等人的研究开辟了此类研究的热潮(Bertero 等,1978),在随后的几十年,近断层速度脉冲对结构影响的研究如火如荼。研究首先从速度脉冲对简单体系地震反应的影响开始(Sasani 等,2000;Alavi 等,2000;Mavroeidis 等,2004),后来逐渐发展到建立实际工程的结构模型,深入研究速度脉冲对钢筋混凝土框架结构(Seneviratna 等,1997;Ghobarah,2004;Ayan 等,2004;Alavi 等,2004;韦韬,2005;赵凤新等,2008)和钢结构(Anderson 等,1987;Hall 等,1995)等结构地震反应的影响。随着分析技术的不断发展,对基础隔震结构(Makris 等,2000;Hall 等,2000;Jangid 等,2001;贺秋梅,2012)和桥梁结构(李新乐等,2004;周媛,2006;贺秋梅,2012)的研究也逐渐深入。上述研究表明,人们对速度脉冲的认识在逐渐加深,且当前的认识已经较为深入,一致认为在结构抗震设计中应考虑速度脉冲对结构弹塑性地震反应的影响。
然而对于峰值速度影响规律的研究来说,仅有速度脉冲的研究是不够的,对其影响规律的研究尚需要深入开展。郝明辉等(2016)研究了峰值速度对单自由度体系地震反应的影响;尤红兵等(2011)开展了地震动峰值速度对地下隧洞内力的影响研究;胡良明等(2019)分析了地震动峰值速度与峰值加速度对重力坝动力响应的影响。峰值位移的影响也需要深入研究。杜修力等(2015)研究了地震动峰值位移对高拱坝地震反应的影响;张郁山等(2011)研究表明地震动峰值位移的增大将会显著增加较长周期结构的弹塑性速度与位移反应;孙忠贤(2009)研究了峰值速度和峰值位移对2 个钢筋混凝土结构地震反应的影响,这是较早开展峰值速度和峰值位移对结构影响规律的研究。杜修力等(2018)研究了峰值速度和峰值位移对地下结构地震反应的影响。地震动峰值速度和峰值位移对结构地震反应的影响机制研究还需要继续探索和推进。
本文将由相同加速度反应谱人工合成的具有不同峰值速度和峰值位移的4 个序列地震动时程作为输入,开展6 层钢结构的弹塑性地震反应分析,从结构变形、结构内力和结构延性等3 个方面分析探讨峰值位移和峰值速度变化对选定结构的弹塑性地震反应的影响。
1 人工地震动合成
地震动时程的选取有2 个来源,一个是现有的强震动观测记录,另一个是人工合成地震动。然而由于已有的强震观测记录中满足要求的地震动时程较少,因此必须借助于人工合成地震动的方法,按照特定的数值分析方法合成多个人工地震动序列,用以模拟地震动时程的特性。人工合成地震动通常被用于结构的地震动输入,用于结构抗震设计中的时程反应分析以及结构的动力学试验。人工合成地震动另一个重要用途是用于研究地震动的工程特性(王彬等,2000;Wang 等,2002;陈健云等,2003)。通过人工合成地震动时程,有效地拓宽了地震动工程特性研究的范围和深度。
基于Fourier 变换与微分运算的线性性质,通过在时域内叠加一系列窄带时程并运用迭代调整技术,赵凤新等(2006)提出了同时满足目标加速度反应谱、目标峰值速度与目标峰值位移的人工地震动时程的合成方法,分析表明所合成的时程对目标值具有较高的拟合精度。本研究基于这种窄带时程叠加法合成多个序列的地震动时程,并开展地震动峰值速度和峰值位移对地震动工程特性的影响研究。
本研究中的目标加速度反应谱的选取参照我国GB 50011-2010《建筑抗震设计规范》(中华人民共和国住房和城乡建设部等,2010)第5.1.5 条规定的地震影响曲线形式,其中峰值加速度(PGA)按照7 度区基本加速度0.10g设防取为1.0 m/s2,场地类别为Ⅱ类,设计地震动分组为第2 组,即特征周期(Tg)取为0.50 s,阻尼比ζ=0.05,目标反应谱曲线如图1 所示。基于该目标反应谱,采用窄带时程叠加的方法人工合成4 个序列的地震动时程,每个序列各有30 条时程,其中各序列的幅值特性如表1 所示。

表1 人造地震动特征Table 1 The characteristics of peak values of artificial ground motion
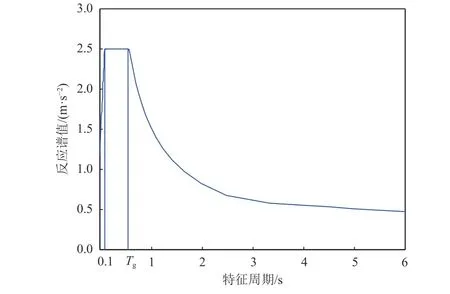
图1 目标加速度反应谱Fig.1 Target acceleration response spectrum
2 参数选择与模型构建
2.1 参数选择
由于结构地震反应参数形式各异,种类较为繁多,因此选择合适的结构地震反应参数至关重要,它直接关系到影响规律的总结和提取。层间位移角也是被广泛应用于结构抗震能力分析的一个参数,Stephens 等(1987)研究了最大层间位移角、塑性层间位移与结构破坏之间的关系,将层间位移角作为限定结构在地震作用下破坏程度的首要参数(任志林,2004)。在各类抗震设计规范中均根据结构层间位移角来判定结构弹塑性状态,通过弹性变形与弹塑性变形验算,以弹性变形限值和弹塑性变形限值为界,保证结构在小震作用下非结构构件不产生明显破坏,大震作用下结构不倒塌,层间位移角反映出结构整体的抗震性能,但有时不能很好地定位结构的薄弱楼层和位置(王飞等,2016)。
良好的延性有助于减小地震作用,吸收和耗散地震能量,避免结构倒塌。结构延性较好说明它能承受较大的非弹性变形且其强度并不明显降低,结构不至发生失稳或倒塌。虽然延性不能很好地反映出结构和构件在地震动作用下的累积破坏,但依然被认为是关键的结构抗震设计参数(Reitherman,1985),并在结构性能评估等领域得到广泛应用(Sordo 等,1989)。由于结构存在多种力-变形关系曲线,因此结构就有多种类型的延性表达形式。如果结构本构关系采用楼层剪力和楼层侧移关系曲线,那么据此便可求出结构的层间侧移延性(张新培,2003;陆新征等,2009)。
2.2 结构概况
美国加州联邦政府办公楼是一座6 层的钢结构,该结构设计建造于1976 年,参照1973 年颁布实施的《统一建筑规范》。结构矩形平面尺寸为36.6 m ×36.6 m,楼板由7.5 cm 的钢板上覆厚度8.2 cm 的轻质混凝土板组成,结构边柱为抗弯构件,用于抗御水平剪切荷载,内柱为铰接构件,主要承担竖向荷载,如图2(a)所示,标准层平面图如图2(b)所示,表2 为梁柱截面配置(Kunnath 等,2004)。

表2 结构梁柱截面配置表Table 2 Section configuration of the beams and columns
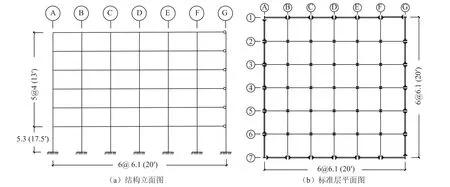
图2 结构立面图及其标准层平面布置Fig.2 Structural elevation and its typical floor plan
该结构所在的城市地震活动频繁,周围活动断层较为密布,是开展地震观测相关研究的适宜位置。加州强震动观测计划项目选择在该政府办公楼的主体结构上布设结构地震反应观测系统以便记录结构在强震中的响应情况,如图3 所示。系统由13 个观测通道组成,传感器分别布置在1 层地面、2 层地面、3 层地面和6层顶板上,以便记录结构在地震中的反应情况。该系统建成后成功记录了多次地震,其中包括1994 年1 月17 日的Northridge 地震(Shakal 等,1994)。结构1 层的最大加速度在南北向和东西向的分量分别为293.0 cm/s2和208.6 cm/s2,而地震波传播到顶层的最大加速度反应在南北向和东西向的分量分别达到441.1 cm/s2和270.7 cm/s2,各层的峰值加速度如表3 所示。Northridge 地震发生后,为保障结构的安全性,结构工程师对该结构开展了现场检查,未发现结构发生明显破坏现象。

表3 楼层加速度反应统计Table 3 Amplitude statistics of floor acceleration response

图3 6 层钢结构地震反应观测系统传感器布设位置Fig.3 The sensor location of the structural seismic response observation system in the 6-story steel building
2.3 结构建模与检验
本文采用OpenSees 作为结构地震反应分析工具,该软件已经成为地震工程领域最具影响力的开放科研平台之一。Anderson 等(1997)对该结构的材料属性和荷载分布情况开展了深入的实验分析和研究,相关成果为广大结构工程师们研究该结构提供了更加详实的资料。Kunnath 等(2005)开展了该结构的数值分析研究,建立了该结构的二维模型并进行结构动力分析,研究结构抗震设计中的地震动选择方法。本研究以Northridge 地震记录为基础,开展结构系统识别研究,构建频率响应函数实施奇异值分解,基于复模态指示函数方法,计算响应函数矩阵的特征值,得到结构前9 阶自振频率,然后在OpenSees 程序中按照结构几何尺寸和材料的动力特性建立三维结构模型,梁柱构件采用基于力的非线性纤维单元Nonlinear Beam Column模拟,梁柱截面宽翼缘钢纤维截面,材料采用最常用的钢材料Steel 01 本构,采用双线型骨架曲线。利用该模型开展结构模态分析,计算出结构的自振频率和振型。对比系统识别出的自振频率和数值分析的自振频率,通过不断调整结构刚度和质量参数,使二者较好的吻合。结构自振频率对比情况如表4 所示,可以发现二者差别较小。以此模型为基础,通过模态分析,计算出该结构的前9 阶自振振型,如图4 所示,振型属性依次为y方向平动、x方向平动和扭转。基于该自振频率,计算瑞雷阻尼,如图5 所示,计算出不同阻尼比下的结构质量和刚度系数。将不同阻尼比下的质量和刚度系数应用于结构动力模型并开展结构反应对比分析,在4%阻尼比下的结构质量和刚度系数分别为0.116 1 和0.011 6,此时结构数值模拟结果与实际地震记录能较好吻合,其他阻尼比下的一致性较差。
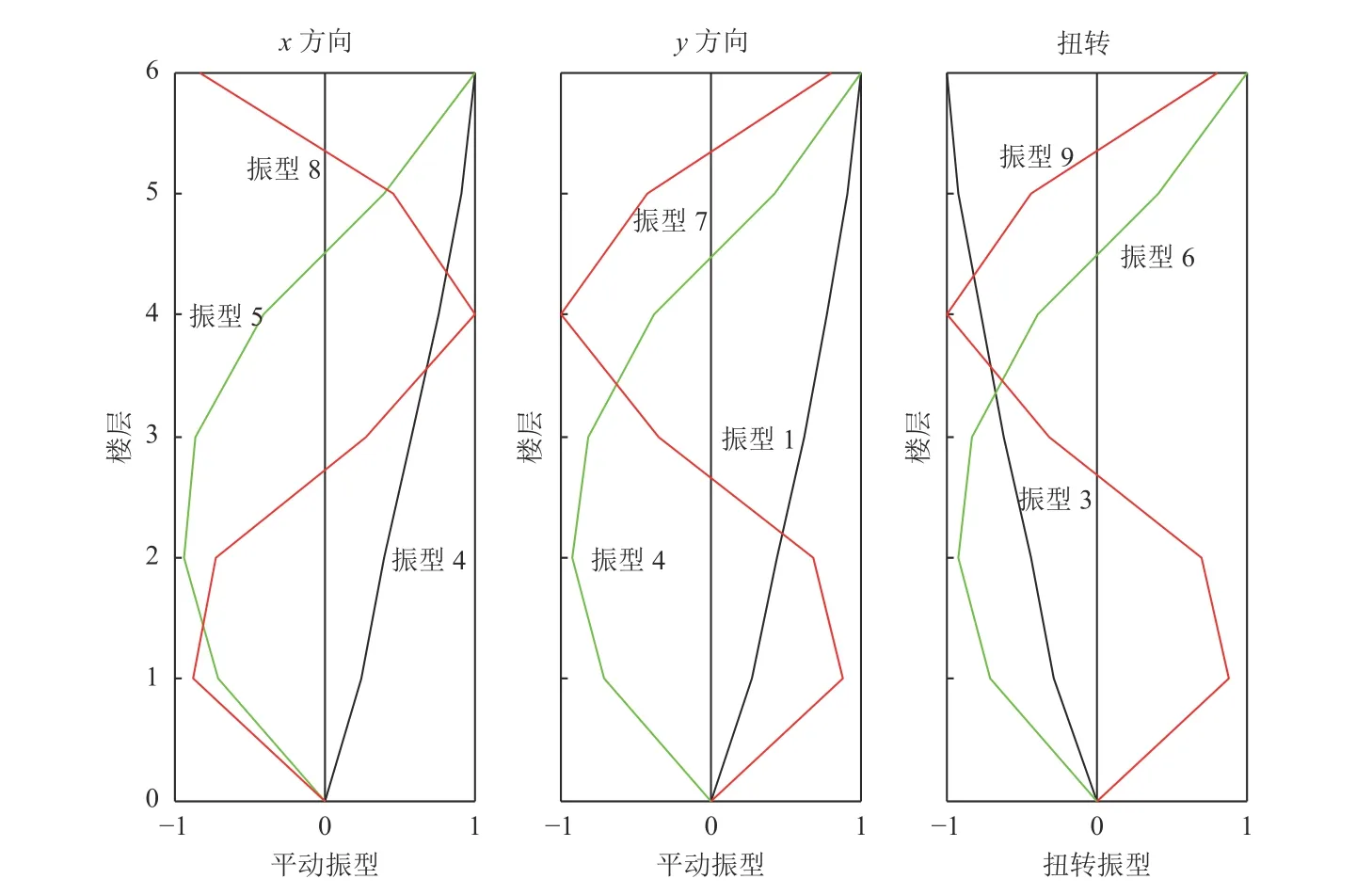
图4 模态分析计算出的结构前9 阶自振振型Fig.4 The first 9 vibration modes of the building identified from modal analysis
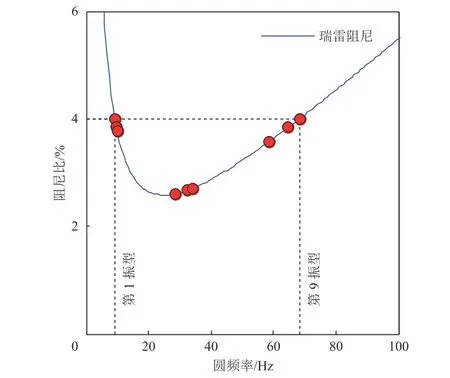
图5 基于自振频率的瑞雷阻尼比计算Fig.5 Rayleigh damping ratio based on the first 9 natural frequencies
将4%阻尼比下的质量系数和刚度系数计算结果,分别设置在结构弹塑性地震反应分析模型中,以记录的1 层的加速度时程地震动作为输入,并开展结构地震反应分析。经过结构弹塑性状态识别后,将分析结果与强震动记录进行对比分析,校核该结构模型与实际结构的一致性。首先对比结构加速度反应分析结果与加速度记录的差异,东西向和南北向的加速度对比如图6 所示。将观测到的结构加速度进行转换计算得到相应的位移记录,并将结构模型的位移反应与计算得到的位移记录时程进行对比,东西向和南北向的位移反应对比如图7 所示。通过结构动力反应的计算值与地震动记录观测值对比,发现不管是东西向还是南北向,二者加速度和位移之间的一致性较高,这说明该结构模型与实际结构的动力特性较为吻合。经过加速度和位移2个参数模型对比校核,认为此模型满足结构动力反应分析研究的精度要求,基于此模型的分析结果可信度较高。
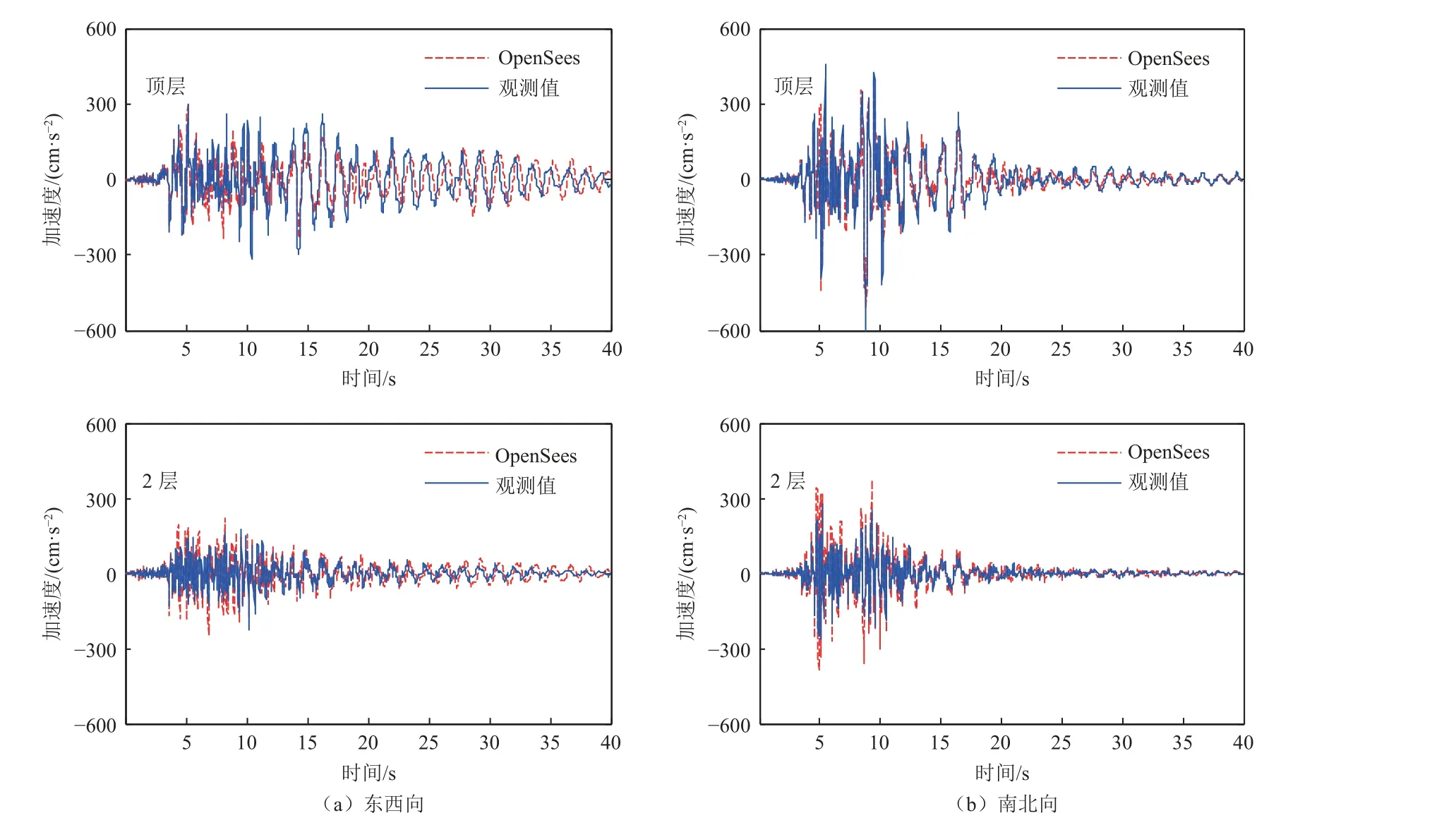
图6 结构数值模拟结果与观测结果的加速度时程对比Fig.6 Comparison of acceleration time history between simulated results and observation results
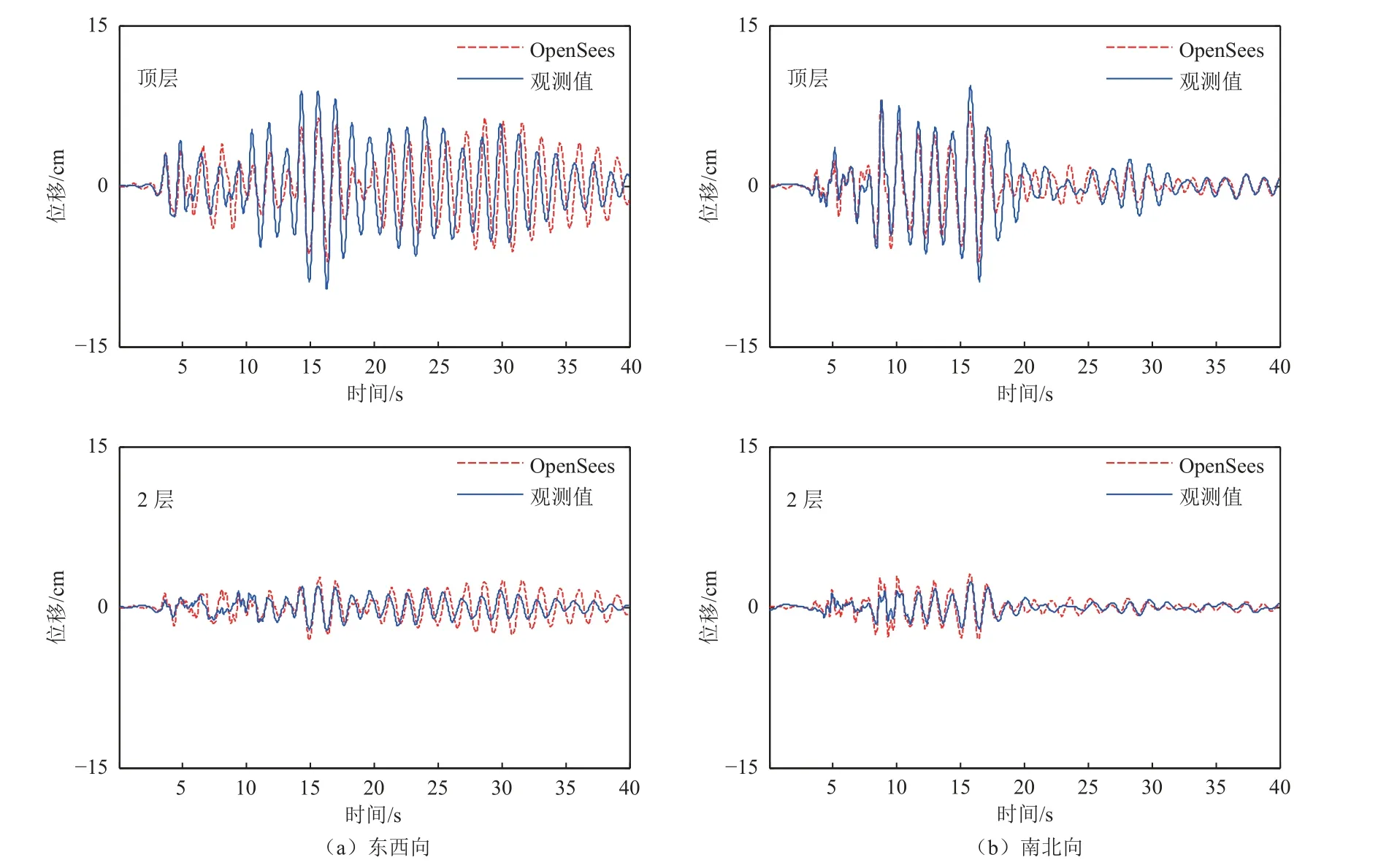
图7 结构数值模拟结果与观测结果的位移反应对比Fig.7 Comparison of displacement time history between simulated results and observation results
3 结构弹塑性分析与对比
将4 个序列的30 组地震动分别分为2 组,通过设置4 和8 的放大倍数将所有地震动的峰值加速度分别标定至400 cm/s2和800 cm/s2,按照双向地震动输入的方式开展该6 层钢结构的地震反应分析,分别计算出同一个加速度水平的不同序列地震动作用下的结构反应,得出15 条加速度时程输入下的结构层间位移角、结构延性系数的结果及其平均值。
3.1 结构层间位移角对比分析
在400 cm/s2地震动作用下,不同序列地震动引起的响应较大的单一水平方向结构层间位移角的计算结果如图8 所示,4 个序列得到的层间位移角的平均值如图9 所示。不同序列地震动作用下结构层间位移角的最大值都集中在1 层上。结构在第1 序列地震动作用下的层间位移角平均值为0.022 28,最小值为0.014 8,最大值为0.030 73,其标准差为0.005 4,层间位移角变异系数为24.2%。而结构在第2 序列地震动作用下的层间位移角的平均值为0.025 34,最小值为0.015 28,最大值为0.047 85,标准差为0.009 4,变异系数为37.1%。结构在第3 序列地震动作用下的层间位移角的平均值为0.022 7,最小值为0.014 07,最大值为0.040 64,标准差为0.007 9,变异系数为34.8%。结构在第4 序列地震动作用下的层间位移角的平均值为0.026 52,最小值为0.017 89,最大值为0.037 19,标准差为0.007,变异系数为26.4%。
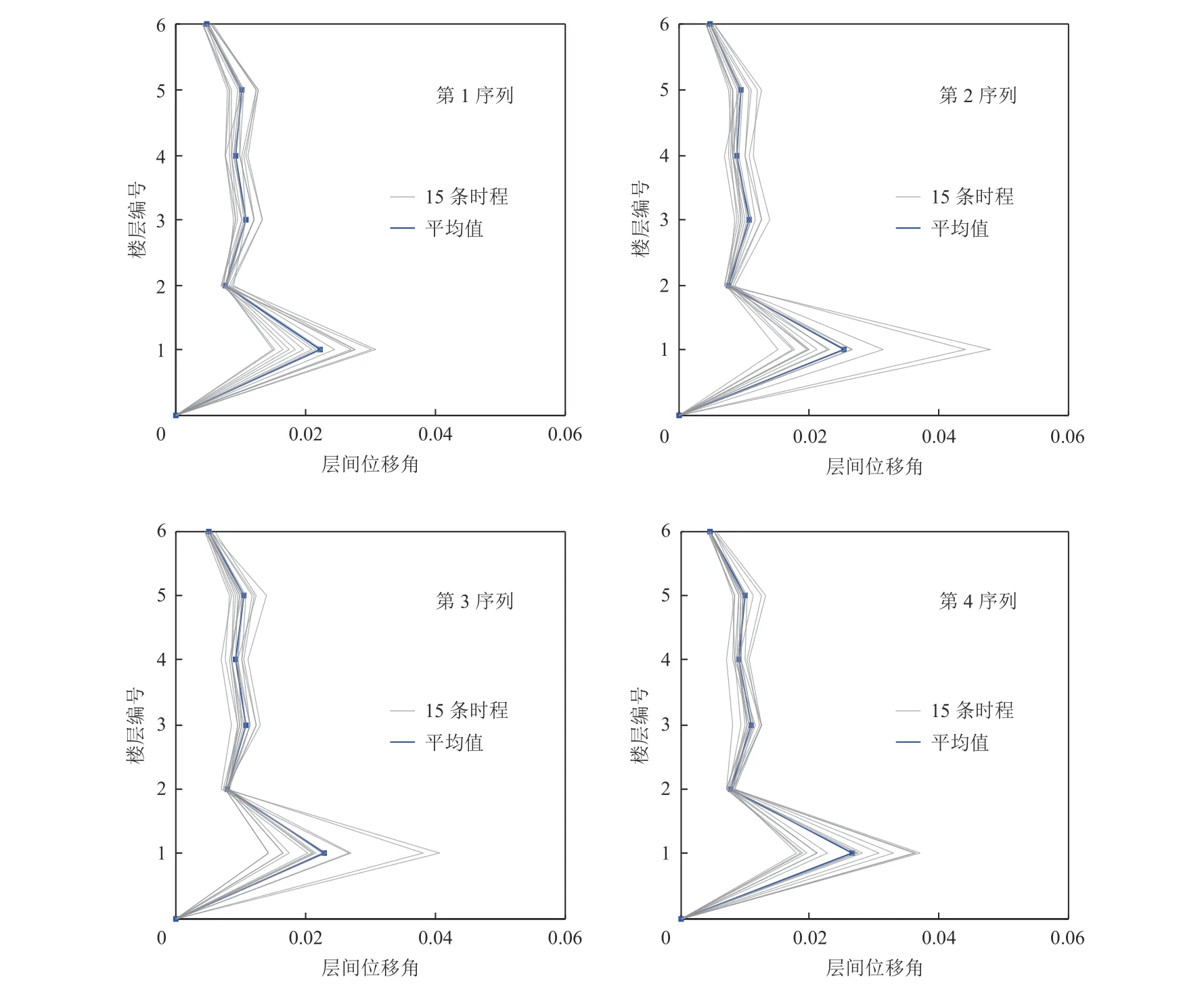
图8 地震动输入为400 cm/s2 时4 个序列地震动作用下的结构层间位移角分布Fig.8 Inter-story drift distributions for four sets of ground motions when the input acceleration amplitude is 400 cm/s2
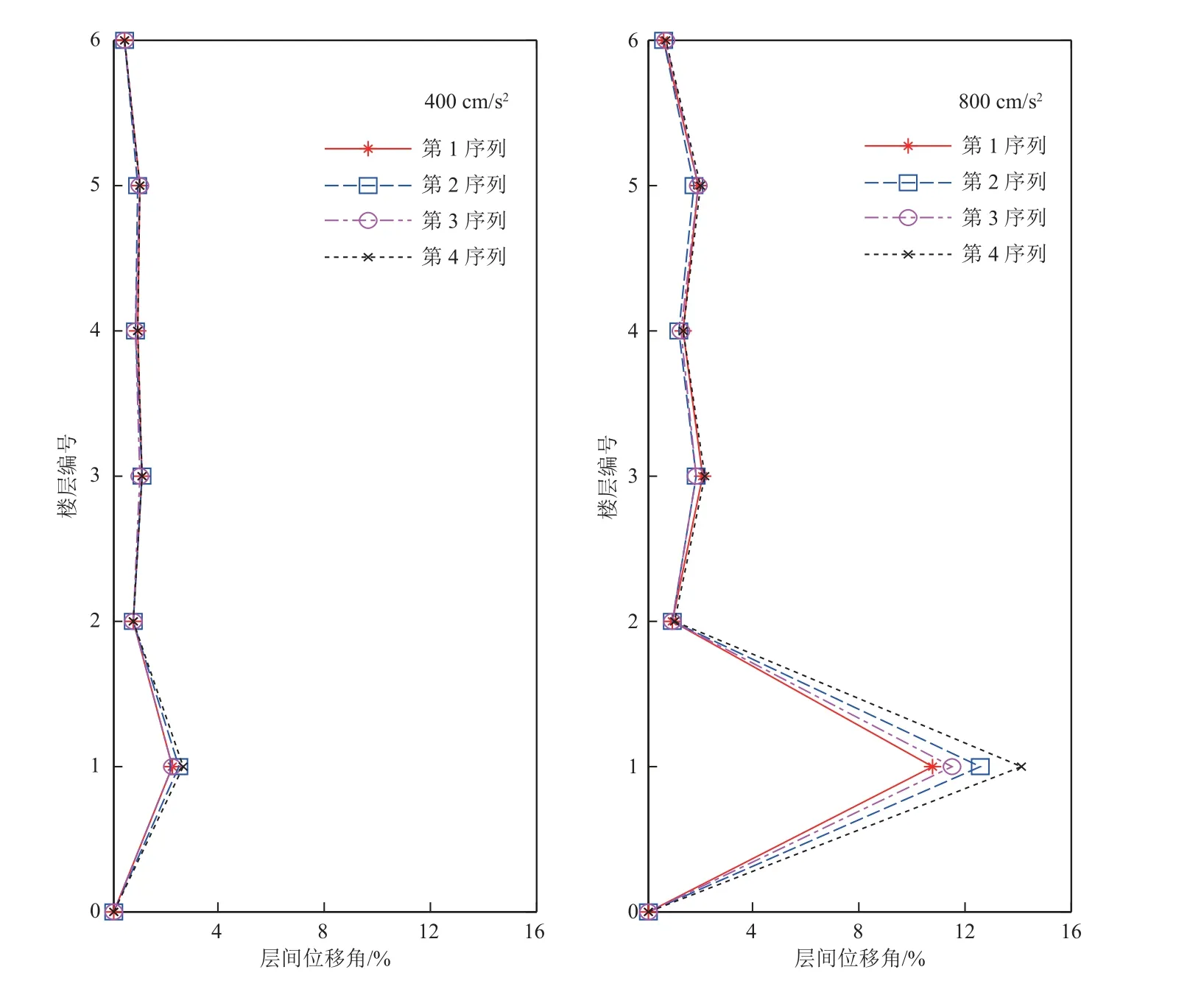
图9 不同地震动输入下的结构层间位移角平均值Fig.9 Average inter-story drift ratio for four sets of ground motions with different input acceleration amplitudes
当峰值加速度增大至 800 cm/s2时,第1 序列地震动作用下的结构1 层的层间位移角平均值为0.107 8,最小值为0.048 18,最大值为0.227 6,标准差为0.064 9,变异系数为60.2%。第2 序列地震动作用下的结构1 层的层间位移角平均值为0.125 6,最小值为0.053 9,最大值为0.238 8,标准差为0.063 8,变异系数为50.8%。第3 序列地震动作用下的结构1 层的层间位移角平均值为0.115 6,最小值为0.051 42,最大值为0.238 1,标准差为0.049 6,变异系数为42.9%。第4 序列地震动作用下的结构1 层的层间位移角平均值为0.141 1,最小值为0.081 23,最大值为0.231 5,标准差为0.044 2,变异系数为31.3%。对比400 cm/s2地震动作用下的结构层间位移角分布情况,输入地震动峰值增加1 倍,结构层间位移角的平均值明显增加,800 cm/s2是层间位移角平均值约为400 cm/s2时的5 倍,充分表明结构的非线性水平较为强烈,且随着输入地震动峰值加速度的增加,结构层间位移角的变异系数也明显增加,最大值达到60.2%,说明同一序列中的不同地震动作用引起的结构层间位移角的差别越来越大。
3.2 延性系数对比分析
当输入地震动加速度峰值标定至400 cm/s2和800 cm/s2时,分别计算不同序列地震动作用引起的结构延性系数的分布、延性系数平均值及其标准差分布,如图10 所示。

图10 不同地震动输入下的结构延性系数平均值Fig.10 Average ductility coefficient for four sets of ground motions with different input acceleration amplitudes
当输入地震动峰值为400 cm/s2时,在第1 序列地震动作用下,结构1 层的延性系数最小值为11.63,最大值为65.28,平均值为30.34,标准差为18.371,计算得出相应的变异系数为60.6%。在第2 序列地震动作用下,结构延性系数的最小值为15.04,最大值为74.96,平均值为34.66,标准差为15.041,相应的变异系数为43.4%。在第3 序列地震动作用下,结构延性系数的最小值为12.67,最大值为58.5,平均值为30.69,标准差为21.682,相应的变异系数为70.0%。最后在第4 序列地震动作用下,结构延性系数的最小值为21.39,最大值为60.4,平均值为38.4,标准差为13.478,相应的变异系数为35.1%。当输入地震动峰值加速度达到800 cm/s2时,第1 序列地震动作用下的结构最大延性系数为30.34,为400 cm/s2时的4.9 倍,第2序列地震动引起的结构最大延性系数为34.66,为400 cm/s2时的5.2 倍。第3 序列地震动引起的结构最大延性系数为30.69,为400 cm/s2时的5.0 倍,第4 序列地震动作用下的结构最大延性系数为38.4,最大值增大为400 cm/s2时的5.4 倍之多,变化较为显著。4 个序列地震动作用下的结构楼层延性的分层一致性较好。第2 序列地震动作用下的最大延性较第1 序列地震动作用下的最大值增加14.2%,而第4 序列地震动引起的结构延性最大值比第1 序列地震动引起的结构地震反应增加25.1%,增加幅度更加明显。对比发现,在800 cm/s2地震动作用下,峰值速度变化引起的结构延性系数变化更大,而峰值位移变化引起的延性系数变化相对较小。
4 结论
本文按照峰值速度和峰值位移的不同将基于相同加速度反应谱合成的人工地震动时程分为4 个序列,将全部地震动时程分别标定至400 cm/s2和800 cm/s2,输入选取的6 层钢结构并开展结构弹塑性地震反应分析,从结构变形、结构内力和结构延性等3 个方面研究了峰值位移和峰值速度变化对结构弹塑性地震反应的影响。
(1)根据布设在该结构上的地震反应系统得到的Northridge 地震强震动记录,分别计算基于强震动记录的结构自振特性、加速度时程和位移时程结果,并用这些结果校正结构数值模型,直至数值模拟计算得出的结构自振特性、加速度和位移时程与地震记录结果之间一致性较好,对比分析认为,本文构建的结构模型满足结构抗震分析的精度要求,可用于后续的弹塑性地震反应分析。
(2)随着输入地震动峰值的增大,地震动峰值速度和位移的差异对结构反应的影响程度逐渐增加。当输入地震动峰值由400 cm/s2增大到800 cm/s2时,第1 序列和第2 序列地震动作用下的结构层间位移角增加16.5%,结构延性系数增加14.2%,而第3 序列和第4 序列地震动引起层间位移角和延性系数增幅分别为22.1%和25.1%。综合对比发现,对于该6 层结构而言,输入地震动峰值速度和峰值位移差异会引起结构弹塑性反应的变化,而峰值速度引起的结构弹塑性反应的增幅比峰值位移引起的增幅更大。
(3)根据结构弹塑性地震反应分析结果,该结构的层间位移角和结构延性系数的最大值都集中在结构1 层,1 层以上各层明显减小,据此判断该6 层结构薄弱层为1 层,需引起注意。

