回归本质 注重联系

缴志清　郝旭岚

摘  要：以2022年全国各地区中考试卷中“图形与坐标”部分试题为载体，依照课程标准的具体要求，结合试题的特点，从七个不同的角度对“图形与坐标”专题内容进行分析，并给出解题方法和备考建议. 把握好这类问题的一般性研究策略，有助于提升学生的数学思维品质，同时有助于教师更好地理解中考改革方向.

关键词：图形与坐标；试题特点分析；优秀试题赏析；备考建议

随着《义务教育数学课程标准（2022年版）》（以下简称《标准》）和《深化新时代教育评价改革总体方案》的颁布，中考改革正在稳步推进.“图形与坐标”是“图形与几何”领域的重要内容，平面直角坐标系是“图形与坐标”内容的重要组成部分，它是数轴的拓展，是沟通代数与几何的桥梁. 数形结合、分类讨论等思想直指该部分中考数学试题命制思路的本质，指导教师在教学中要不断优化教学过程，提炼出一般性的思维策略，从而进一步提升学生的数学思维品质.

一、试题特点分析

1. 凸显核心素养的考查

2022年中考数学试题的命制以《标准》为指导思想，贯彻德智体美劳全面发展的教育方针，落实立德树人根本任务. 2022年全国各地区中考“图形与坐标”试题设计灵活多样，更加注重指向数学核心素养的考查，以达到减少教学中让学生“机械刷题”的目的. 在落实“双减”政策、引导教学、减少死记硬背方面做出了新的探索.

2. 展现立德树人的要求

2022年全国各地区中考“图形与坐标”试题结合数学学科特点，展现了立德树人的要求. 例如，湖北宜昌卷第10题以学生的教室平面图为背景，建立适当的平面直角坐标系，求与小丽相邻且能比较方便地讨论交流的同学座位的坐标，这既要求学生养成平时善于观察的学习习惯，又让学生体会到了讨论交流是促进学习发展的一种很好的手段.

3. 体现数学与实际生活的融合

2022年全国各地区中考“图形与坐标”试题还展现了数学在实际生活中的应用. 例如，山东烟台卷第12题和湖北鄂州卷第14题都是以象棋棋盘为背景，建立适当的平面直角坐标系，求某棋子的坐标. 这两道试题把平面直角坐标系与象棋文化相结合，考查了学生应用数学知识解决实际生活问题的能力.

4. 落实课程标准的要求和数学本质的考查

初中阶段，“图形与几何”领域包括“图形的性质”“图形的变化”和“图形与坐标”三个主题，分别从演绎证明、运动变化、量化分析三个方面研究图形的基本性质和相互关系. 这三个方面的知识又是相辅相成、相互影响的. 因此，试题的呈现形式要综合这三个方面的知识.《标准》中，“图形与坐标”的具体内容包括两个方面：一是图形的位置与坐标；二是图形的运动与坐标.

2022年全国各地区中考“图形与坐标”试题的考查符合《标准》要求，关注数学本质，立足学生数学核心素养的发展. 例如，天津卷第10题将一个等腰三角形与平面直角坐标系相结合，考查了三角形各个顶点的位置；山东泰安卷第14题将平行四边形与平面直角坐标系相结合，考查平行四边形的性质、点和线段的平移规律. 这些试题都重点考查了学生的理性思维能力及分析和解决问题的能力. 对于“图形与坐标”部分的试题，必须利用好平面直角坐标系这个沟通代数与几何的桥梁，学会用坐标表示图形上点的位置、用坐标表达图形的变化、用坐标表达简单图形的性质，即用代数方法研究图形，体会数形结合的数学思想，提高分析和解决问题的能力.

二、优秀试题分析

2022年全国各地区中考数学试卷中，“图形与坐标”内容主要考查的知识点包括以下几个方面：（1）用坐标表示图形的位置；（2）用坐标表示图形的性质；（3）用坐标表示图形的变化；（4）用坐标表示动点的变化规律；（5）用坐标表示动点的函数图象；（6）平面直角坐标系中图形性质与函数图象的综合问题；（7）平面直角坐标系中的作图问题；等等. 该部分试题的考查形式灵活，涉及选择题、填空题、解答题，其中蕴含了数形结合、分类讨论、转化、建模等数学思想，以及推理能力、几何直观、空间观念、模型观念等素养.

1. 用坐标表示图形的位置

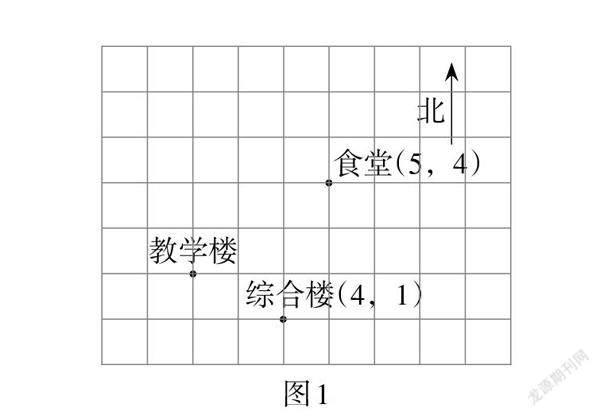
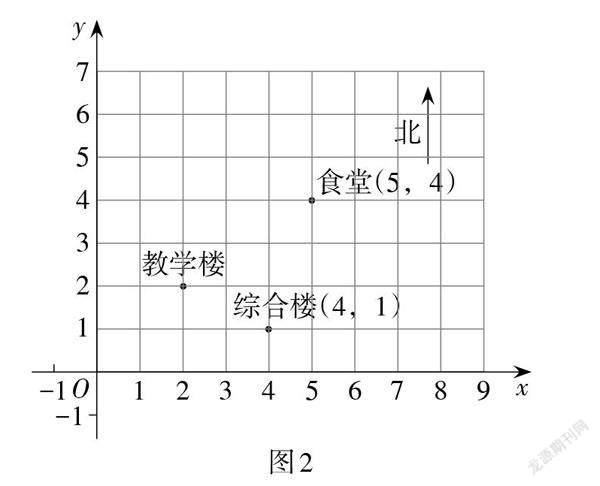
例1 （广西·柳州卷）如图1，这是一个利用平面直角坐标系画出的某学校的示意图，如果这个坐标系分别以正东、正北方向为x轴、y轴的正方向，并且综合楼和食堂的坐标分别是（4，1）和（5，4），则教学楼的坐标是（  ）.

（A）（1，1） （B）（1，2）

（C）（2，1） （D）（2，2）

目标解析：此题主要考查在实际问题中建立适当的平面直角坐标系描述物体的位置. 这类试题直接考查点的位置与坐标，以及基础知识和基本技能，属于简单题.

解法分析：如图2，根据综合楼和食堂的坐標分别是（4，1）和（5，4），建立适当的平面直角坐标系，可得教学楼的坐标是（2，2）. 故此题答案选D．

试题分析：这类试题一般源于教材，在教材课后习题的基础上进行改编. 平面上的点与坐标之间是一一对应关系，根据两个点的坐标可以建立适当的平面直角坐标系，然后再用坐标描述点的位置. 根据题意建立适当的平面直角坐标系是解决此类试题的关键．

类题赏析：类似的试题还有山东烟台卷第12题、浙江金华卷第7题、湖北宜昌卷第10题、甘肃兰州卷第14题等，这些试题体现了实际生活与数学相联系的特点，体现了数学既源于生活，又应用于生活.

2. 用坐标表示图形的性质

例2 （天津卷）如图3，△OAB的顶点O（0，0），顶点A，B分别在第一、四象限，且AB⊥Ox，若AB = 6，OA = OB = 5，则点A的坐标是（  ）.

（A）（5，4） （B）（3，4）

（C）（5，3） （D）（4，3）

目標解析：此题考查的是图形的性质与坐标，以及学生的推理能力和运算能力，旨在发展学生的几何直观素养.

解法分析：如图4，设AB与x轴交于点C.

因为OA = OB，OC⊥ AB，AB = 6，

所以AC =[12]AB = 3.

由勾股定理，得OC =[OA2-AC2=52-32]= 4.

所以点A的坐标为（4，3）.

故此题选择D．

试题分析：此题是求点的坐标. 解题思路是先根据题意求出线段OC的长，再根据点的位置确定这个点的坐标. 解题过程中用到了等腰三角形“三线合一”的性质和勾股定理. 这类试题的考查难度一般较小，但是涉及的图形性质较多，需要在熟练掌握图形性质的基础上求线段的长度，从而得出点的坐标.

类题赏析：类似地，青海卷第5题、吉林卷第12题、贵州铜仁卷第2题、贵州黔西南州卷第10题也考查了图形的性质与坐标的知识. 其中，吉林卷第12题还考查了圆的垂径定理.

3. 用坐标表示图形的变化

（1）坐标与图形的对称.

例3 （浙江·丽水卷）三个能够重合的正六边形的位置如图5. 已知点B的坐标是（[-3]，3），则点A的坐标是       ．

目标解析：此题主要是用坐标描述几何图形的对称性，考查学生的几何直观素养.

解法分析：根据正六边形的性质，可得点A和点B关于原点对称. 因为点B的坐标是（[-3]，3），所以点A的坐标是（[3]，-3）. 故此题的答案为（[3]，-3）．

试题分析：此题中，利用正六边形的对称性能够知道点A和点B关于原点对称. 解决这类试题既要能准确判断图形的对称性，还要熟练掌握关于x轴、y轴、原点对称的点的坐标特点.

类题赏析：类似地，浙江台州卷第6题也考查了坐标与图形的对称的知识.

（2）坐标与图形的平移.

例4 （山东·临沂卷）如图6，在平面直角坐标系中，△ABC的顶点A，B的坐标分别是A（0，2），B（2，-1）. 平移△ABC得到△A′B′C′，若点A的对应点A′的坐标为（-1，0），则点B的对应点B′的坐标是

目标解析：此题考查的是用坐标描述图形的平移. 这类试题利用平面直角坐标系将几何与代数完美地结合在了一起，充分体现了数形结合思想.

解法分析：由题意可知，将点A从（0，2）平移至（-1，0），可以看作是将△ABC先向下平移2个单位长度，再向左平移1个单位长度（或者先向左平移1个单位长度，再向下平移2个单位长度）. 再由点B的坐标为B（2，-1），可得平移后的对应点为B′（1，-3）. 故此题的答案为（1，-3）．

试题分析：此题由点A的平移可以判断出点B的平移规律，从而利用平移前后点的坐标特点来解决问题. 解决这类试题最重要的是掌握平移的性质和平移前后对应点坐标的变化规律.

类题赏析：类似地，山东泰安卷第14题、辽宁大连卷第13题、广西百色卷第10题、山东威海卷第6题等也考查了坐标与图形平移的知识点. 其中，山东泰安卷第14题需要利用平行四边形两组对边分别平行的性质，可以看作将线段DC平移到线段AB，从而利用平移的性质解决问题.

（3）坐标与图形的旋转.

例5 （黑龙江·绥化卷）如图7，线段OA在平面直角坐标系内，点A坐标为A（2，5），线段OA绕原点O逆时针旋转90°，得到线段OA′，则点A′的坐标为（  ）.

目标解析：此题考查的是用坐标描述图形的旋转. 学生在解决此类问题时，要灵活应用相关知识点，体会各个知识点之间的联系，以及数学思维的深刻性，彰显数学的本质.

解法分析：如图8，过点A作AB⊥Ox于点B，过点A′作A′C⊥Ox于点C.

因为点A的坐标为A（2，5），

所以OB = 2，AB = 5.

由题意，得∠AOA′ = 90°，OA = OA′．

所以∠AOB + ∠A′OC = 90°．

因为∠A′OC + ∠A′ = 90°，

所以∠A′ = ∠AOB．

在△A′OC和△OAB中，

因为[∠A′= ∠AOB，∠A′CO=∠OBA=90°，OA′=AO，]

所以△A′OC ≌ △OAB（AAS）．

所以A′C = OB = 2，OC = AB = 5.

所以点A′的坐标为（-5，2）．

故此题选择A．

试题分析：此题是在过点A作AB⊥Ox于点B，过点A′作A′C⊥Ox于点C后，利用“一线三等角”和三角形全等，求出A′C和OC的长度，从而得出点A′的坐标. 这类试题往往具有以下特点：（1）旋转角度为特殊角或者旋转到某个特殊位置；（2）问题设置一般是求图形旋转前后点的坐标；（3）有时会在网格的背景下进行旋转. 解决这类试题常作的辅助线是过某点向x轴或y轴作垂线，利用图形的性质求解相应的线段长度，这是解题的关键. 这里要注意抓住旋转的两大特点：（1）对应点到旋转中心的距离相等；（2）两组对应点分别与旋转中心的连线所夹的角相等. 解决此类问题时还经常会用到三角形全等的性质和勾股定理等知识.

类题赏析：类似地，江苏苏州卷第8题、黑龙江牡丹江卷第19题、四川内江卷第9题、湖南湘潭卷第17题也考查了坐标与图形旋转的知识点. 其中，江苏苏州卷第8题要分别过点C作x轴、y轴的垂线段，然后利用等边三角形的性质和勾股定理，把相关线段的长度用含m的代数式进行表示，再利用线段之间的关系建立方程模型，求出m的值．

（4）坐标与图形的位似.

例6 （贵州·黔西南州卷）如图9，在平面直角坐标系中，△OAB与△OCD位似，位似中心是坐标原点O. 若点A（4，0），点C（2，0），则△OAB与△OCD周长的比值是       ．

目标解析：此题考查的是用坐标描述图形的位似，以及学生的识图能力，旨在发展学生的几何直观素养.

解法分析：因为△OAB与△OCD位似，位似中心是坐标原点O，而点A（4，0），点C（2，0），

所以相似比为4∶2 = 2∶1.

所以△OAB与△OCD周长的比值为2．

故此题的答案为2．

试题分析：此题考查平面直角坐标系中的图形位似的问题. 如果位似变化是以原点为位似中心，相似比为k，那么位似图形对应点的坐标之比等于k或-k．熟练掌握位似变化前后点的坐标的变化规律，是解决此类问题的关键.

类题赏析：类似地，四川巴中卷第6题也考查了位似图形与平面直角坐标系相结合的问题.

（5）坐标与锐角三角函数.

例7 （湖北·荆州卷）如图10，在平面直角坐标系中，点A，B分别在x轴负半轴和y轴正半轴上，点C在OB上，OC∶BC = 1∶2，连接AC，过点O作OP∥AB交AC的延长线于点P．若P（1，1），则tan∠OAP的值是（    ）.

（A） [33] （B） [22]

（C） [13] （D） 3

目标解析：此题属于图形的变化与坐标的内容，这里主要考查的是坐标与锐角三角函数的结合.

解法分析：如图11，过点P作PQ⊥Ox于点Q，

因为OP∥AB，

所以∠CAB = ∠CPO，∠ABC = ∠COP.

所以△OCP ∽ △BCA.

所以CP∶AC = OC∶BC = 1∶2 .

因为∠AOC = ∠AQP = 90°，

所以CO∥PQ.

所以OQ∶AO = CP∶AC = 1∶2 .

因为P（1，1），所以PQ = OQ = 1.

所以AO = 2.

所以tan∠OAP =[PQAQ=12+1=13].

故此题答案选C.

试题分析：解决这类试题的关键是根据题目的已知条件发现图形中的相似或全等模型，利用常用的辅助线作法“向坐标轴作垂线”构建直角三角形，利用图形的性质求解相关线段的长度，然后利用锐角三角函数的定义解决问题.

类题赏析：四川泸州卷第11题也考查了平面直角坐标系与锐角三角函数相结合的問题.

4. 用坐标表示动点的变化规律

例8 （河南卷）如图12，在平面直角坐标系中，边长为2的正六边形ABCDEF的中心与原点O重合，AB∥Ox，交y轴于点P. 将△OAP绕点O顺时针旋转，每次旋转90°，则第2 022次旋转结束时，点A的坐标为（  ）.

（A）（[3]，-1） （B）（-1，[-3]）

（C）（[-3]，-1） （D）（1，[3]）

目标解析：此题主要考查点的运动与坐标的变化规律，以及学生的观察能力、推理能力、归纳概括能力等，属于综合类试题.

解法分析：如图13，由正六边形的性质可得A（1，[3]）. 再由每次旋转90°，可知每旋转4次为一个循环. 由2 022 ÷ 4 = 505…2，可知点A2 022与点A2重合，故求出点A2的坐标可得答案. 因为点A2与点A关于原点O对称，所以A2（-1，[-3]）. 因此第2 022次旋转结束时，点A的坐标为（-1，[-3]）. 故此题答案选B.

试题分析：此题以正六边形为背景，由正六边形的性质可以得出坐标的变化规律．解决这类试题的关键是正确识别图形，利用图形的性质等知识找到动点的变化规律，难度较大.

类题赏析：类似地，黑龙江齐齐哈尔卷第17题、贵州毕节卷第20题、湖北荆门卷第15题、贵州黔西南州卷第20题、山东菏泽卷第14题也都考查了坐标与动点的变化规律. 其中，黑龙江齐齐哈尔卷第17题先利用函数解析式可得点A，B的坐标，从而得出∠BAO = 30°，进而根据三角函数的定义，得出点的坐标的变化规律，最终得到答案.

5. 用坐标表示动点的函数图象

例9 （山东·潍坊卷）如图14，在[?]ABCD中，∠A = 60°，AB = 2，AD = 1，点E，F在?ABCD的边上，从点A同时出发，分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动，到达点C时停止，线段EF扫过区域的面积记为y，运动时间记为x，能大致反映y与x之间函数关系的图象是（  ）.

目标解析：此题主要考查的是动点的函数图象问题. 这类试题考查学生的画图、识图能力，以及分析问题和解决问题的能力，属于综合类试题，难度较大.

解法分析：过点F作FH⊥AB于点H. 如图15，当0 ≤ x ≤ 1时，在Rt△FAH中，AF = x，∠A = 60°，则FH = AF·sin A =[32]x. 所以线段EF扫过区域的面积y =[12]x·[32]x =[34]x2，图象是开口向上的抛物线的一部分.

如图16，当1 < x ≤ 2时，过点D作DP⊥AB于点P，则DP = AD·sin A =[32]. 所以线段EF扫过区域的面积y =[12]（x - 1 + x） ×[32]=[32x]-[34]，图象是y随x的增大而增大的线段.

如图17，当2 < x ≤ 3时，过点E作EG⊥CD于点G，则CE = CF = 3 - x. 所以EG =[32]（3 - x）. 所以线段EF扫过区域的面积y = 2 ×[32-12]（3 - x） ×[32]（3 - x） =[3-34]（3 - x）2，图象是开口向下的抛物线的一部分.

试题分析：此题以平行四边形为背景，考查了动点问题中的函数图象、平行四边形的性质、三角形的性质、一次函数和二次函数的图象及性质，具有较强的综合性. 解决此类问题的关键是根据图形的特点和动点的运动情况进行分类讨论，通过分析各个时间段的图形特点，分别写出各个时间段的函数表达式. 在考场上，对于此类选择题，有时候并不需要写出最终的函数表达式，可以通过排除法判断各个时间段的函数圖象特点，从而得出答案.

类题赏析：辽宁鞍山卷第8题、山东菏泽卷第8题、内蒙古鄂尔多斯卷第10题都考查了动点的函数图象问题.

6. 平面直角坐标系中图形性质与函数图象的综合问题

例10 （四川·泸州卷）如图18，在平面直角坐标系xOy中，矩形OABC的顶点B的坐标为（10，4），四边形ABEF是菱形，且tan∠ABE =[43]. 若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分，则直线l的解析式为（  ）.

（A）y = 3x （B）y =[-34x+152]

（C）y = -2x + 11 （D）y = -2x + 12

目标解析：此题考查的是坐标与图形的性质和函数图象相结合的综合问题. 这类试题考查了学生的推理能力及建立函数模型的能力，是对数学核心素养的深度考查.

解法分析：如图19，连接OB，AC，交于点M，连接AE，BF，交于点N，则直线MN为符合条件的直线l.

因为四边形OABC是矩形，所以OM = BM．

因为点B的坐标为B（10，4），

所以M（5，2），AB = 10，BC = 4．

因为四边形ABEF为菱形，所以BE = AB = 10．

过点E作EG⊥AB于点G，

在Rt△BEG中，因为tan∠ABE =[43]，所以[EGBG=43].

设EG = 4k，则BG = 3k.

所以BE =[EG2+BG2]= 5k.

因为5k = 10，所以k = 2.

所以EG = 8，BG = 6. 所以AG = 4．

所以E（4，12）．

因为点B的坐标为B（10，4），且AB∥Ox，

所以A（0，4）．

因为点N为AE的中点，所以N（2，8）．

设直线l的解析式为y = ax + b（a ≠ 0），

所以[5a+b=2，2a+b=8.] 解得[a=-2，b=12.]

所以直线l的解析式为y = -2x + 12.

故此题选择D．

试题分析：此题要平分一个矩形和一个菱形所组合图形的面积，利用两个图形的中心对称性质，分别求出矩形OABC和菱形ABEF的中心的坐标，利用待定系数法，求经过两个图形中心的直线解析式即可得到答案. 解决此类问题的关键是充分利用图形的性质和函数图象性质求解出特殊点的坐标，难度较大.

类题赏析：类似地，黑龙江齐齐哈尔卷第15题、浙江绍兴卷第15题、浙江宁波卷第16题、四川乐山卷第16题等，都考查了平面直角坐标系中的综合问题.

7. 平面直角坐标系中的作图问题

例11 （广西·河池卷）如图20，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（4，1），B（2，3），C（1，2）．

（1）画出与△ABC关于y轴对称的△A1B1C1；

（2）以原点O为位似中心，在第三象限内画一个△A2B2C2，使它与△ABC的相似比为2∶1，并写出点B2的坐标．

目标解析：此题考查了在平面直角坐标系和网格中的作图问题. 此题既考查了作轴对称图形和位似图形. 除此之外，还可以考查作中心对称图形、旋转后的图形等. 这类试题主要考查学生的动手操作能力，要想画出准确的图形，必须熟练掌握图形的性质.

解法分析：（1）如图21，△A1B1C1为所求；

（2）如图21，△A2B2C2为所求，点B2的坐标为（-4，-6）.

试题分析：此类试题还可以与圆的知识结合，如弧长公式、扇形的面积等. 解决这类问题的关键是掌握图形变化前后的坐标变化规律，先确定关键点，再确定图形.

类题赏析：陕西卷第19题、黑龙江龙东地区卷第22题也考查了在平面直角坐标系和网格中的作图问题.

三、复习备考建议

1. 注重基础，回归数学本质

“图形与坐标”这部分内容的本质是用坐标表达图形的性质和图形的对称、旋转、平移变化的规律. 在中考复习备考时，教师要引导学生回归数学本质，注重基础知识. 学生要熟练掌握三角形、平行四边形、矩形、菱形、正方形等基本图形的性质；充分理解平面直角坐标系中各象限点的坐标特点，以及将图形进行对称、平移、旋转变化时坐标的变化规律；要熟练掌握建立平面直角坐标系、描点、画图等基本操作. 复习这些基础知识时，要以教材为主，充分发挥教材的导向作用；要重视坐标与图形的性质和变化等知识之间的联系，从“大单元”的角度深度学习，注重知识的整体性. 教师要引导学生用好平面直角坐标系这个联系代数和几何的桥梁，能用代数方法表达图形的性质和变化.

例如，内蒙古赤峰卷第18题考查了抛物线与[x]轴的交点、二次函数图象上点的坐标特征、等腰直角三角形的判定与性质、轴对称的性质等知识. 解决此类问题的关键是熟练掌握二次函数图象上点的坐标特征、轴对称性质等数学本质内容．解决此题不仅要利用数形结合思想直观感知试题中的一些关系，而且要注意利用二次函数进行计算和说理时，需要在求函数解析式的基础上进行逻辑推理，从而探究出所求点的坐标. 这也落实了《标准》中的新增内容——了解代数推理.

2. 注重方法，提高思维品质

众所周知，数学是思维的科学，数学是思维的体操. 数学教学的核心任务之一是要培养学生的思维能力，使学生在掌握数学基础知识的过程中，学会感知、观察、归纳、类比、想象、抽象、概括、推理、证明和反思的逻辑思考的基本方法.

对于“图形与坐标”这部分内容，在复习备考时，要注意解题方法的提炼. 在解题时，要注意对条件展开合理的联想，形成条件关系网. 例如，看到求点的坐标的题目，对条件展开联想：能否作坐标轴的垂线？能否构造三角形全等或相似？能否利用勾股定理建立方程？对于给出的一个问题需要尝试从不同的角度去思考，从而得出不同的解决问题的方法.

数学学习是一个不断优化的过程，只有通过不同方法的比较，才能优化解题的思路. 在平时做题时，学生要注意总结如何思考、如何转化、如何作辅助线等问题，使数学学习超越具体的知识和技能，由反思解决具体题目的过程和方法，过渡到提炼出一般性的思维策略，在训练过程中把逻辑思维能力推向多方向、多层次，举一反三，触类旁通，从题海中解脱出来，从而减轻学习负担，进一步提升数学思维的品质.

3. 注重理解，提升运算能力

《标准》指出：运算能力，主要是指根据法则和运算律进行正确运算的能力. 能够明晰运算的对象和意义，理解算法与算理之间的关系；能够理解运算的问题，选择合理简洁的运算策略解决问题；能够通过运算促进数学运算能力的发展，运算能力有助于形成规范化思考问题的品质，养成一丝不苟、严谨求实的科学态度.

“图形与坐标”这部分的试题往往需要结合勾股定理、锐角三角函数、三角形全等或相似、圆的相关性质、弧长和扇形面积公式等知识，求解相关线段的长度或图形的面积. 在这个过程中会应用到解方程、二次根式的化简、锐角三角函数的计算等代数推理. 因此，提升运算能力对这部分试题的解答会有很大的帮助. 在复习备考过程中，要认真总结运算错误的原因，如公式记忆不准、缺乏简便运算的技巧、算理不清等. 例如，对弧长及扇形面积公式记忆不准确，导致计算错误. 对此，在学习时要重视公式的形成过程，在彻底了解公式的来龙去脉后，对公式的记忆会更加准确，即便生疏了，自己也能推导出来. 又如，用勾股定理计算PA7 =[242-122]，可以运用平方差公式进行简便计算，即[242-122=24+12×24-12=][36×12=123]. 这样的运算过程显然计算量更小，不易出错. 所以在学习平方差公式或者勾股定理的课程时，要注意掌握类似的计算方法，提高运算的准确性，从而提升运算能力.

四、典型模拟题

以上總结了2022年全国各地区中考试卷针对“图形与坐标”这一模块的考查方向，下面向大家展示四道模拟试题，有不妥之处，还望各位同仁批评指正.

1. 点[M-tan60°，cos45°]关于[x]轴对称的点的坐标是（    ）.

（A）[32， 12] （B）[-33，-12]

（C）[-3， 22] （D）[-3，-22]

答案：D.

【评析】此题将点的坐标与三角函数相结合，考查了学生对相关基础知识的掌握情况.

2. 在平面直角坐标系中，直线y = 2x + 3与x轴的交点坐标是（    ）.

（A）（0，3） （B）（3，0）

（C）[0，-32] （D）[-32，0]

答案：D.

【评析】此题考查了一次函数与坐标轴的交点坐标，是对学生基础知识和基本技能的考查.

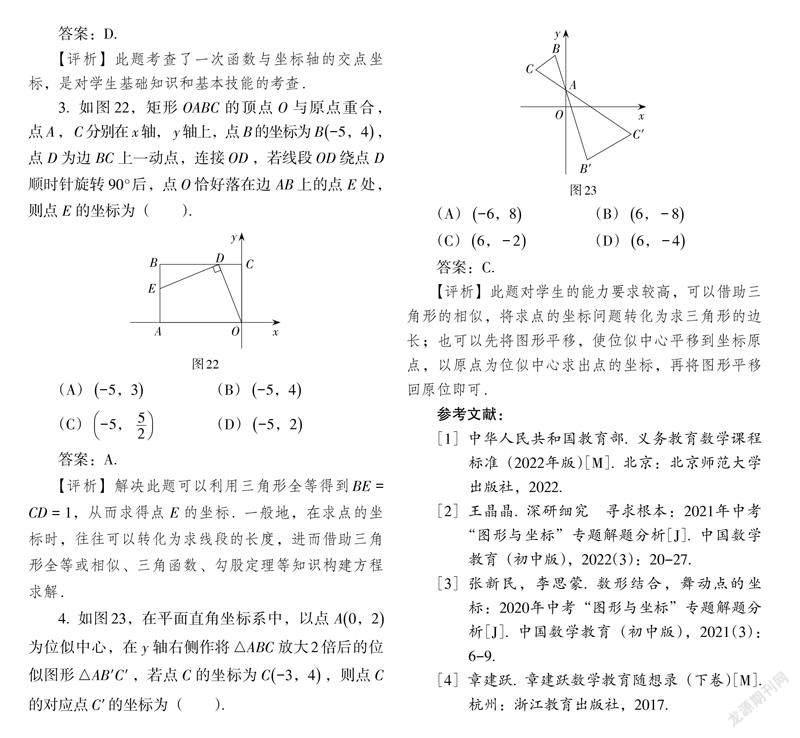
3. 如图22，矩形[OABC]的顶点[O]与原点重合，点[A]，[C]分别在[x]轴，[y]轴上，点[B]的坐标为[B-5，4]，点[D]为边[BC]上一动点，连接[OD]，若线段[OD]绕点[D]顺时针旋转[90°]后，点[O]恰好落在边[AB]上的点[E]处，则点[E]的坐标为（    ）.

（A）[-5，3] （B）[-5，4]

（C）[-5， 52] （D）[-5，2]

答案：A.

【评析】解决此题可以利用三角形全等得到BE = CD = 1，从而求得点[E]的坐标. 一般地，在求点的坐标时，往往可以转化为求线段的长度，进而借助三角形全等或相似、三角函数、勾股定理等知识构建方程求解.

4. 如图23，在平面直角坐标系中，以点[A0，2]为位似中心，在[y]轴右侧作将[△ABC]放大2倍后的位似图形[△AB′C′]，若点[C]的坐标为[C-3，4]，则点[C]的对应点[C′]的坐标为（    ）.

（A）[-6，8] （B）[6，-8]

（C）[6，-2] （D）[6，-4]

答案：C.

【评析】此题对学生的能力要求较高，可以借助三角形的相似，将求点的坐标问题转化为求三角形的边长；也可以先将图形平移，使位似中心平移到坐标原点，以原点为位似中心求出点的坐标，再将图形平移回原位即可.

参考文献：

［1］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［2］王晶晶. 深研细究  寻求根本：2021年中考“图形与坐标”专题解题分析［J］. 中国数学教育（初中版），2022（3）：20-27.

［3］张新民，李思蒙. 数形结合，舞动点的坐标：2020年中考“图形与坐标”专题解题分析［J］. 中国数学教育（初中版），2021（3）：6-9.

［4］章建跃. 章建跃数学教育随想录（下卷）［M］. 杭州：浙江教育出版社，2017.

作者简介：缴志清（1961— ），男，正高级教师，主要从事课程、教学与考试评价研究；

郝旭岚（1971— ），女，高级教师，主要从事中学数学教学研究.