逆高斯纹理复合高斯杂波对异常样本稳健的三分位点估计方法

水鹏朗 田 超 封 天

(西安电子科技大学雷达信号处理国家级重点实验室 西安 710071)

1 引言

IG-CG( Compound-Gaussian model with Inverse Gaussian texture)是复合高斯海杂波模型的重要类型之一[1–3]，其能够作为K-分布[4,5]，广义Pareto强度分布[6]，对数正态纹理复合高斯模型(Compound-Gaussian model with LogNormal texture, LN-CG)[7]的重要补充刻画中高距离分辨率的海杂波。而且IG-CG模型下的近最优计算可实现的相干检测器的两种形式已经在最近被发现[8,9]。因此，对于高分辨海用雷达，IG-CG模型在目标检测中的使用的重要前提是在海杂波IG-CG模型参数的精确估计[10]。在CFAR (Constant False Alarm Rate)检测中，参数估计精度决定了虚警率的控制精度，参数估计越准确，虚警率控制越精准[8,11]。而且使用匹配于杂波逆形状参数的最优、近最优相干检测器时，不精确的参数估计会导致最优或近最优检验统计量失配，带来性能损失。由于雷达接收的数据中包含了高幅度的异常样本，其主要来自海面目标、岛礁等的强回波，传统基于样本矩和迭代最大似然(Iterative Maximum Likelihood, IML)估计的方法[12]由于其对异常样本的敏感性难以使用。

文献[12]基于数据样本分位点对异常样本的稳健性，提出了对异常样本稳健的双分位点(Bi-Percentile, BiP)估计方法。该方法能够在存在异常样本的情况下稳健估计海杂波IG-CG模型的尺度参数和逆形状参数。仿真和实测数据处理结果表明：两个分位点的位置明显影响估计对异常样本稳健性和精度。受K-分布下对异常样本稳健的三分位点估计方法[13]的启发，本文提出了估计IG-CG分布逆形状参数和尺度参数对异常样本稳健的三分位点(Tripercentile, Tri-per)估计方法。按照文献[12]中的结果，两个分位点的比率是逆形状参数的单调函数，不同的分位点位置对应不同的逆形状参数估计器。从大量的仿真实验发现了达到逆形状参数估计最小均方根误差的双分位点位置的经验公式。在逆形状参数估计中，上分位点的位置由其对异常样本的稳健性要求确定，下分位点位置由经验公式确定，从而得到了逆形状参数估计的最优参数设置。基于估计的逆形状参数，进一步确定具有最小均方根误差的第三分位点位置得到尺度参数的估计。这样得到了具有最优分位点位置设置的三分位点参数估计方法，其明显改善了参数估计性能。

本文内容安排如下。第2节回顾了海杂波的IGCG幅度模型以及对异常样本稳健的双分位点估计方法。第3节提出了具有最优分位点位置设置的三分位点估计方法。第4节基于仿真和实测数据检验了提出方法的性能并与已有方法进行对比。第5节总结了全文的工作。

2 海杂波的IG-CG分布模型与双分位点参数估计

复合高斯模型是公认的描述海杂波的有效模型，该模型中海杂波表示为两个独立随机变量的乘积，反映功率起伏的纹理分量和描述散斑的复高斯分量，海杂波表示为

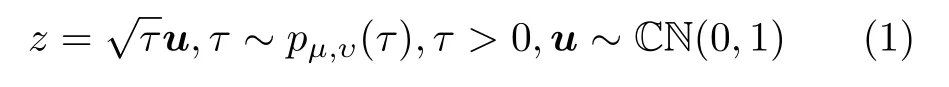
其中，μ和υ分别是纹理分布的尺度(杂波功率)和逆形状参数(传统形状参数的倒数)，u是零均值单位方差的复高斯随机变量。纹理的概率密度函数取不同分布类型对应于不同的复合高斯模型。典型的，Gamma分布纹理、逆Gamma分布纹理、逆Gaussian分布纹理和对数正态纹理分别对应于K-分布[4,5]、广义Pareto强度分布[6]、IG-CG分布[1]和LN-CG分布[7]。IG-CG幅度分布的概率密度函数(Probability Density Function, PDF)和累积分布函数(Cumulative Density Function, CDF)的表达式分别为其中，r=|z|表 示幅度，µ表示尺度参数。逆形状参数越大，幅度分布拖尾越重，海杂波的非高斯性越强。当υ=0时，式(2)退化为瑞利分布，杂波是高斯杂波。当样本为纯杂波数据时，矩估计方法(Method Of Moment, MOM)[1]和IML估计方法[12]能够得到IG-CG模型参数的高精度估计。由于实际回波数据不可避免含异常样本，MOM和IML估计方法由于对异常样本敏感，估计值会严重偏离其真实值。文献[12]提出的IG-CG分布参数的BiP估计方法，由于其使用数据的样本分位点进行参数估计，其估计性能对异常样本稳健[14]。

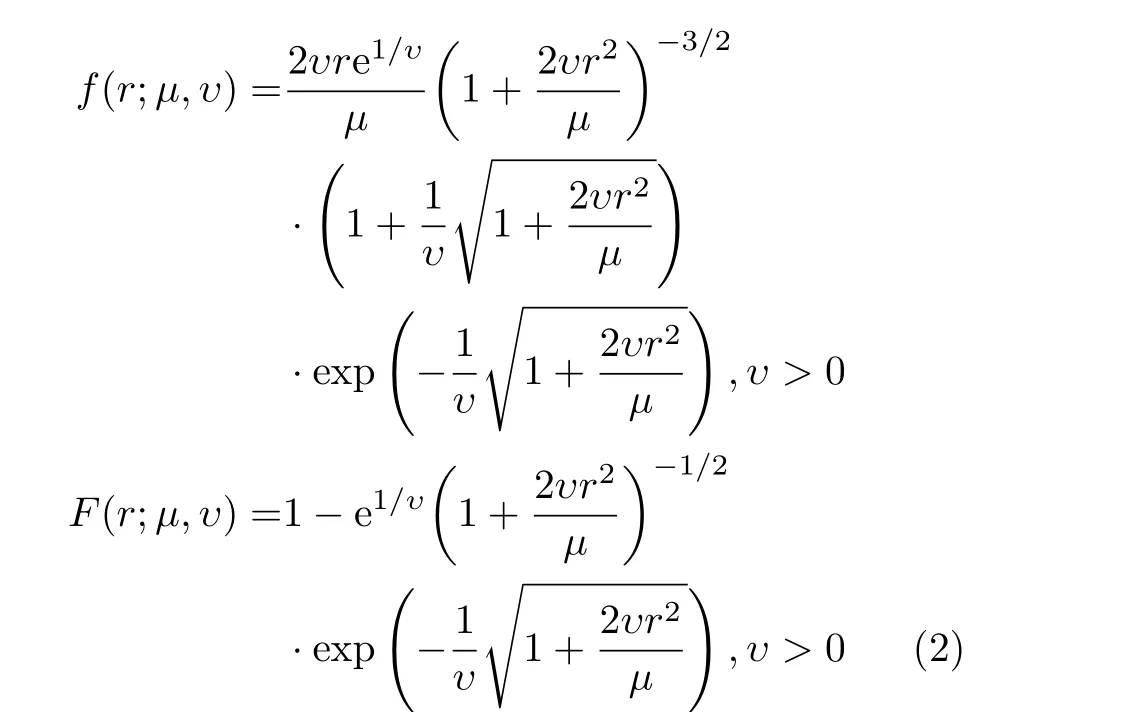
对于任意值0 <α<1 ， 位置为α的分位点rα是方程

其中，W(x)是Lambert W-函数,y=xex函数的反函数。对于任意的0<α<β<1，可以得到两个分位点的比是与尺度参数无关的逆形状参数的单调函数[12]，即

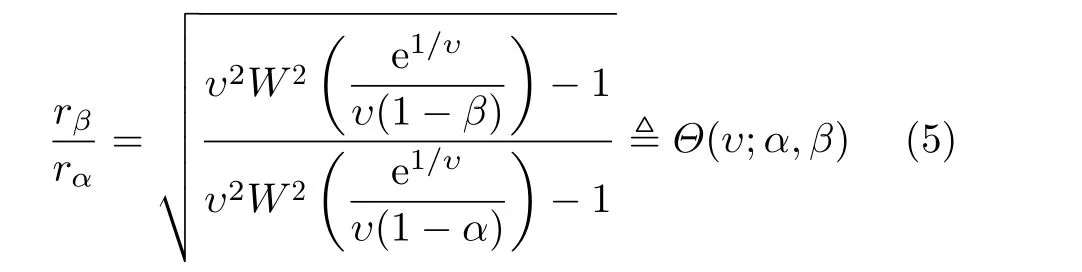
因此，函数Θ(υ;α,β)的反函数存在，记作Λα,β(⋅)。由于缺乏解析表达式，使用时对给定的0<α<β<1，函数Λα,β(⋅)可以通过查表法实现。当逆形状参数已知，尺度参数可以从任意分位点估计，例如

当式(5)和式(6)中的分位点被样本分位点代替后，就得到了异常样本稳健的BiP估计方法[12]。设{ri,i=1,2,...,N}是 幅度样本，{r(i),i=1,2,...,N}是把样本从小到大排列得到的序列，IG-CG分布模型的双分位点参数估计方法的表达式为

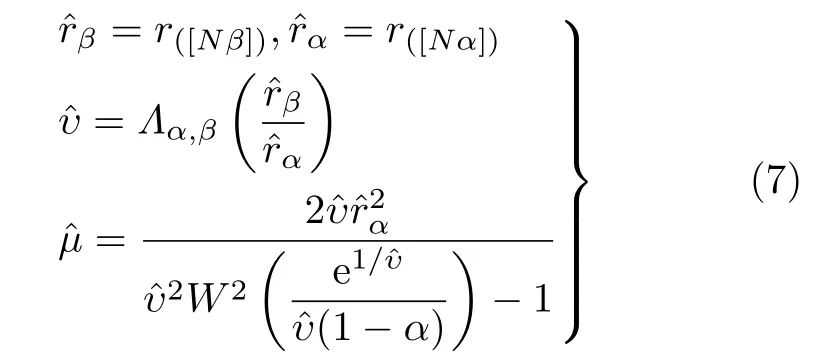
其中，[x]表示取最接近x的整数，rˆα和rˆβ分别是下和上样本分位点。显然，不同的0<α<β<1对应于不同位置的BiP估计。上分位点位置β的选择基于对异常样本的稳健性，1–β必须小于数据中异常样本可能的最大比例。下分位点位置α的选择也明显影响估计性能[12]。

3 分位点位置优化配置与三分位点估计方法

BiP估计方法中, 分位点位置α和β会影响参数估计的性能。受K-分布三分位点估计方法[13]的启发，本文通过3个分位点位置的优化设置改进参数估计的精度。首先，通过两个分位点位置的优化设置改进逆形状参数的估计精度，然后在逆形状参数估计的基础上寻找第三分位点的最优位置改进尺度参数的估计精度。

按照式(7)的估计，当数据样本中不存在异常样本时，对于给定的分位点位置α和β，逆形状参数的估计性能可以用相对均方根误差衡量，它是位置参数和样本数目的函数，记为

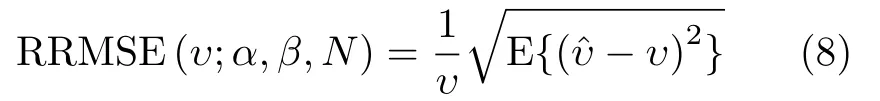
其中，υˆ是逆形状参数的估计值。然而，很难得到上面相对均方根误差的解析表达式，位置参数α和β的优选只能依赖于Monte-Carlo试验得到的估计值。首先，α和β的优选不应该依赖于逆形状参数本身的值，因为其估计之前是未知的。需要找出对所有逆形状参数公用的最优的位置参数设置。不失一般性，假定海杂波逆形状参数υ具有先验分布pυ(υ)，那么对于给定的样本数N，分位点位置参数的优选归结为优化问题

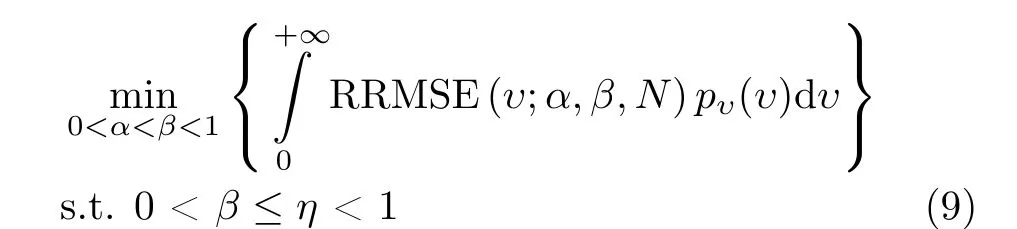
其中，η是控制估计对异常样本稳健性的参数。一般来说，数据中异常样本的比例要小于1–η。

本文通过Monte-Carlo试验的方法验证上面的近似结果，假设逆形状参数γ服从区间[0,100]上的均匀分布。对给定的α,β和N，计算优化问题式(9)中的目标函数的值，计算积分时通过按照均匀分布随机生成105个随机的逆形状参数的值取其相对均方根误差的平均值实现。其中样本数分别取做N=1000, 3000, 5000, 10000，下分位点位置α在区间[0.1,0.6]上均匀取值，其间隔为0.01，上分位点位置β在区间[α+0.1,0.99]上均匀取值，取值间隔为0.01。如图1所示，本文画出了4个样本数情况下目标函数的等值线图。在每条等值线上，总体的逆形状参数估计相对均方根误差是相等的。图中紫色曲线由每个β值下总体相对均方根误差达到最小的α的最优分位点位置(α,β)构成。可以看到：在N很大时，式(9)中逆形状参数估计的相对均方根误差与N无关。为了获得最优参数设置的经验公式，本文通过二次函数拟合最优参数设置中α和β的关系，得到了经验公式

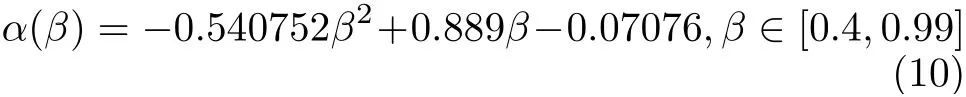
拟合曲线在图中用黑色曲线表示，可以看到拟合曲线和紫色曲线很好吻合。

可以发现，从图1中的经验公式的曲线正好是综合相对均方根误差的等值线与β=常数的垂直线的共切点组成的曲线。由于所有等值线都是凸曲线，因此经验公式曲线上的每个点都意味着：选择的分位点位置是所有具有相同综合相对均方根误差的位置配置中具有最小β值的配置。而小的β值意味着逆形状参数估计对异常样本更稳健。换句话说，就是分位点最优位置选择就是在估计性能固定的情况下选择对异常样本最稳健的配置，这能够从优化问题式(9)的对偶规划得到合理性解释。下面研究当逆形状参数估计得到情况下尺度参数估计性能的优化问题。不同于BiP估计中，尺度参数从下样本分位点和估计的逆形状参数进行估计，本文选择第3个样本分位点估计尺度参数。按照式(6)，当逆形状参数已知时，尺度参数的平方根正比于第3个分位点的值。按照样本分位点的渐进公式，当尺度参数的平方根从第3个位置在γ的样本分位点进行估计时，估计是渐进高斯的，即

图1 实验选取最佳分位点组合

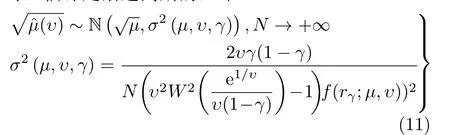
按照式(11)够大时，尺度参数的估计性能由正态分布的变差系数(CV)决定

于是，第3个分位点的最优位置就是给定逆形状参数时函数h(υ,γ)的最小值点，即

可以证明式(15)中的函数γ(υ)满足

按照式(16)函数在两个极端情况下的情况以及图2中数值计算得到的曲线式(15)的图像，本文用下面形式的指数函数拟合曲线

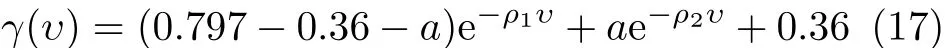
通过最小二乘拟合得到参数a=0.06923,ρ1=0.4824,ρ2=0.03648。可以看到：图2中的拟合曲线和从式(16)的数值计算得到的曲线拟合得很好。此外，由于第3分位点的位置γ(υ)≤0.797是远离1的，尺度参数的估计对异常样本是稳健的。

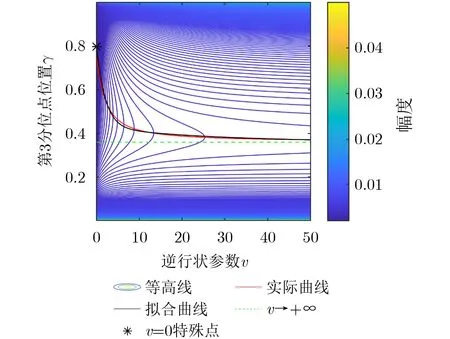
图2 第3分位点相对误差等高线图

按照式(7)、式(10)和式(17)，从一组含有异常样本的数据中估计IG-CG幅度分布的参数时，首先按照数据中最大可能的异常样本百分比，确定上分位点的位置β，然后按照式(10)确定下分位点位置α。形状按照式(7)的BiP估计方法进行估计，最后尺度参数从式(17)确定的第3分位点位置进行估计，即

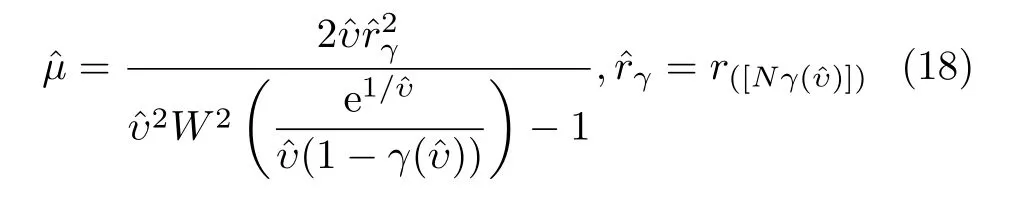
4 实验结果与性能比较

本节通过仿真和实测数据检验三分位点估计方法的性能并与已有的估计方法进行比较。主要比较方法是两个参数的RRMSE和数据的CDF和CDF之间的K-S距离，它定义为

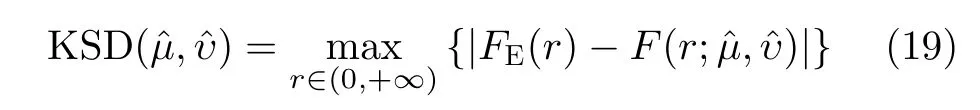
其中，FE(r)是从数据得到的经验幅度累积分布，F(r;µˆ,υˆ)是估计参数得到的拟合分布。

4.1 仿真数据实验与性能比较

仿真实验中，海杂波数据中添加2%的异常样本，异常样本的功率是海杂波功率的[20,400]倍并且按照均匀分布随机生成。参数估计的样本数设置为N=5000，逆形状参数取值0.1～15，间隔为0.1均匀取值，杂波数据的尺度参数固定为1。本文使用1-2阶矩估计方法(1-2 order Method Of Moment, MOM12)[2]，2-4阶矩估计方法(2-4 order Method Of Moment, MOM24)[1], IML估计方法[12],具有α=0.5，β=0.95的BiP估计方法[12]，和提出的三分位点估计方法到仿真数据上。为保持相同的稳健性，三分位点估计方法上分位点位置β=0.95，下分位点位置和第3分位点位置按照式(10)和式(17)设置。存在异常样本的情况下，5个估计方法得到的逆形状参数、尺度参数的相对均方根误差和数据经验CDF和拟合CDF的平均K-S距离如图3所示。这里K-S距离对比横坐标为0.1～5的逆形参范围。由于MOM12，MOM24和IML估计对于异常样本非常敏感，2%高功率异常样本的存在使得参数估计性能急剧变差。这3个估计方法的相对均方根误差、平均K-S距离与两个基于分位点的对异常样本稳健的估计方法相比就不在一个数量级上。为了演示这种性能差异，在3个子图的右下角通过小图显示了两类估计方法在性能上的巨大差异。从图3可以看出：当异常样本存在的条件下，基于样本分位点的估计方法性能良好，这类方法对异常样本的稳健性源于样本分位点或序贯统计量对异常样本的稳健性[14]。相对于采用固定分位点位置的BiP估计方法[12]，提出的具有分位点位置优化的三分位点估计方法获得了较为明显的性能改善。

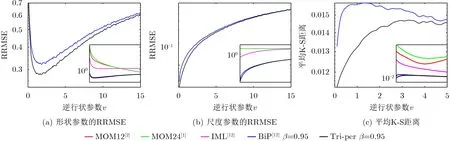
图3 有异常样本条件下5种估计方法逆形状参数的估计性能对比

4.2 实测数据性能比较实验

在实测数据实验中选取了IPIX数据集[15]和CSIR数据库[16]各一组X波段高分辨率海杂波数据。其中IPIX数据集的数据文件名为“19980223_184853_ANTSTEP”。

数据的距离分辨率3 m，HH极化模式，脉冲重复频率1000 Hz，数据使用了27个相邻距离门在9-34 s内的雷达回波。数据中配试目标是位于第21距离门的漂浮小船，平均信杂比22.4 dB。区域A为杂波参考(其用IML估计方法估计的参数作为真值)，区域B为纯杂波数据区域，区域C包含了2%的异常样本。区域A, B, C的海杂波数据的参数估计样本数分别为5000, 5600, 2857。由图4和表1观察可知，纯杂波区域B内，IML估计误差最小且5种估计误差区分差别不大，意味着没有异常样本情况下，5种估计方法的性能都是可以接受的。而在含异常样本的区域C内，传统的IML, MOM24和MOM12估计方法由于对异常样本敏感，估计值严重偏离真值，而提出的三分位点估计相比于BiP估计方法估计性能受影响更小并达到了最好的估计性能。

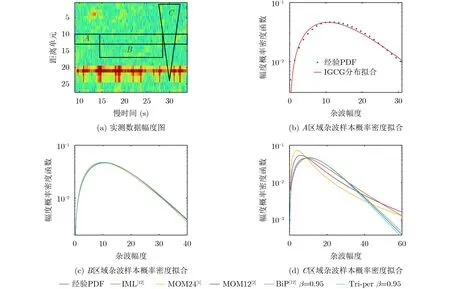
图4 IPIX数据库一组HH极化数据上5种参数估计方法的性能比较

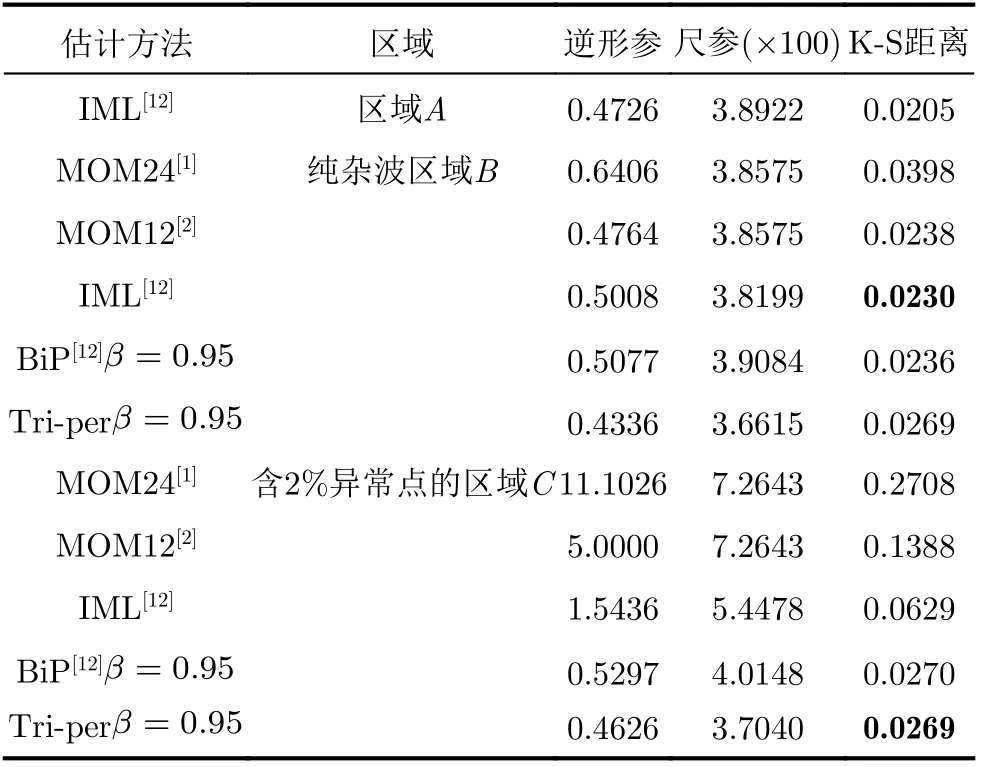
表1 IPIX实测数据(19980223_184853_ANTSTEP)的估计结果

为了更全面地考察估计方法，另选了南非CSIR数据库[16]的一组X-波段数据进行实验。

实验结果如图5所示，对应的参数估计性能结果如表2所示。图5(a)为实测数据幅度图，该数据距离分辨率为15 m，数据的极化方式为VV，数据中配试小船的平均信杂比为19.3 dB，其雷达回波可作为异常样本检验估计方法的稳健性。其中A,B, C区域各包含4600, 6000, 5201个样本，C区域含约2%的异常样本。由图5和表2观察可知，在纯杂波区域B内，IML估计误差最小且5种估计方法的性能差异不大。而在含异常样本的区域C内，传统的IML, MOM24和MOM12估计方法性能急剧下降，提出的三分位点估计在估计稳健性上要优于BiP估计方法并明显好于传统估计方法。

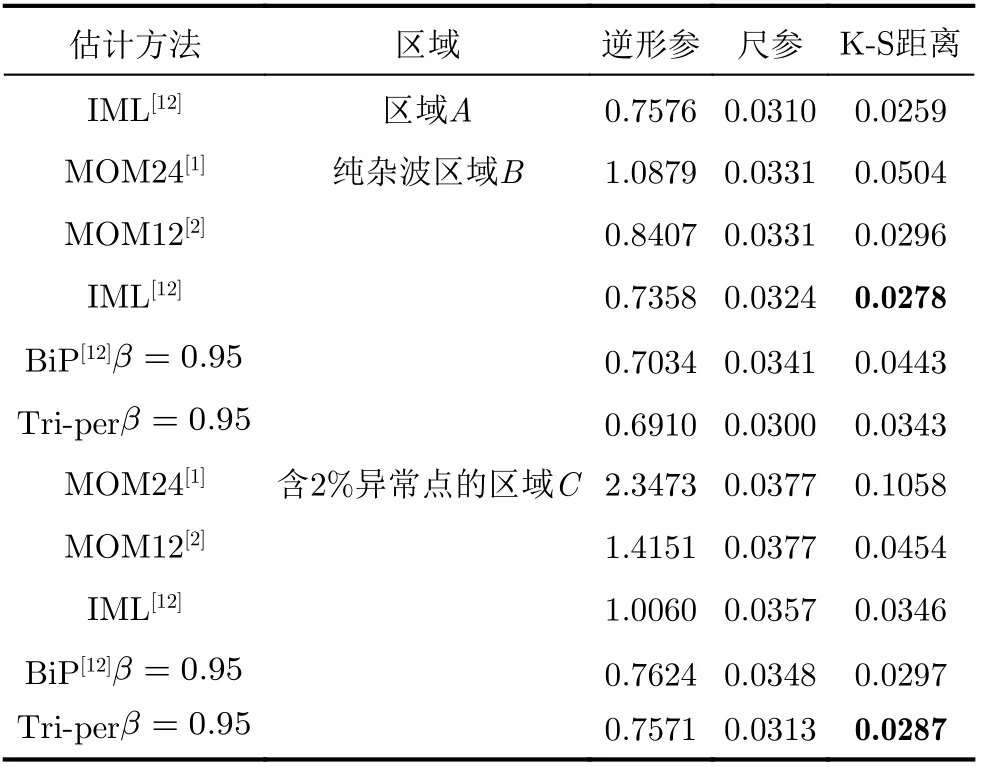
表2 南非CSIR实测数据(TFA10_001.01)的估计结果

图5 CSIR数据库一组VV极化数据上5种参数估计方法的性能比较

文献[12]中IML方法在纯海杂波下性能最好，但其易受异常样本影响。而BiP估计方法属稳健估计方法，但分位点位置的选择没有优化，遭受了一些性能损失。提出的方法通过前两个分位点位置的优化改善逆形参的估计性能，通过第三分位点位置的优化改进尺度参数的性能。实测数据的实验结果表明：两个参数的估计性能都得到了改善。

5 结束语

海用雷达目标检测面临着复杂的海洋环境，海杂波建模和参数估计是有效目标检测的基础。由于不可避免的目标、岛礁等雷达强回波对海杂波模型参数估计性能产生了严重的影响。本文提出了针对异常样本存在情况下的海杂波IG-CG模型稳健的三分位点估计方法。该方法通过数值计算和曲线拟合优化分位点位置提高参数估计精度。基于仿真数据和实测数据的实验结果表明提出的估计方法在存在异常样本的条件下达到更好的参数估计性能。