双选信道下OCDM系统低复杂度均衡

宁晓燕 宋禹良 孙志国 孙晶晶

(哈尔滨工程大学信息与通信工程学院 哈尔滨 150001)

1 引言

随着通信技术的不断发展，信息的传输需要更高的速率来满足我们的日常需求，正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)在4G和5G通信中发挥着重要作用[1]。然而，在自由空间无线传输过程中，信号传输会受到各种干扰的影响，如多径效应、多普勒频移等。OFDM的子载波是余弦信号，对多普勒频移非常敏感，当信道为双选信道时，其性能将受到严重影响。

Chirp信号的自相关函数有着良好的时间分辨率，对多普勒频移不敏感，具有脉冲压缩和扩频特性，在雷达和通信系统中发挥着重要作用[2]。结合OFDM的抗干扰特性和Chirp信号的抗多普勒特性，提出了OFDM-Chirp系统[3]，但它占用了大量的带宽资源，因此没有得到广泛的应用。

最近，正交Chirp复用(Orthogonal Chirp Division Multiplexing, OCDM)的概念被提出[4]，基于菲涅尔变换的OCDM可以实现Chirp扩频(Chirp Spread Spectrum, CSS)的最大频谱效率，并通过在同一带宽内对多个Chirp波形进行正交复用来实现最大的通信效率。OCDM信号可以有效地利用多径分集，表现出比OFDM信号更强的抗衰落能力，提高通信数据传输的可靠性[5]。OCDM系统已应用于光通信和水声通信[6,7]，现有的研究主要集中在频率选择性衰落信道中。文献[4]提出了一种抵消相位的MMSE均衡算法，作为OCDM系统线性MMSE均衡的基础。文献[8]提出了基于基扩展模型(Basis Expansion Models, BEM)的近似带状矩阵MMSE频域均衡算法，并且介绍了一种时域LSQR(Least Square QR)算法。

在高速移动场景下，由于多普勒效应的影响，可以对均衡算法做进一步的改进。文献[8]介绍了一种适用于求解大型稀疏矩阵的时域LSQR算法，但其忽略了噪声的影响，而实际系统中的噪声是必须考虑的因素，需要对其进行修正，本文提出一种基于近似带状矩阵的阻尼LSQR(Band Damped-LSQR, BD-LSQR)算法进行均衡。为了缓解时变信道中的载波间干扰(Inter Carrier Interference,ICI)，本文在近似带状矩阵[9]的基础之上，结合判决反馈均衡，通过LSQR算法进行迭代计算，并借助LDLH分解简化运算，提出一种LSQR-BDFE算法，这是该算法在OCDM系统中的首次应用。仿真结果表明，双选信道下，OCDM系统比OFDM系统有着更好的BER性能，所提出的LSQR-BDFE算法和BD-LSQR算法，比MMSE均衡算法有着性能优势。

2 系统模型

OFDM的核心是傅里叶变换，快速傅里叶逆变换(Inverse Fast Fourier Transform, IFFT)过程取代了N个独立的载波源，降低了OFDM系统实现的复杂性。OCDM的核心是菲涅尔变换，它用离散菲涅尔逆变换(Inverse Discrete Fresnel Transform,IDFnT)代替IFFT过程，这使得在不同的系统中有着不同的子载波。在OFDM系统中，子载波是余弦信号，而在OCDM系统中，子载波是Chirp信号。

2.1 OCDM原理

OCDM利用菲涅尔变换形成一组正交的线性Chirp信号，将通信信息加载到该组Chirp信号的幅度和相位中。在相同带宽上，多个Chirp波形之间正交复用，形成一串在时间和频谱上重叠的Chirp信号，如图1所示。

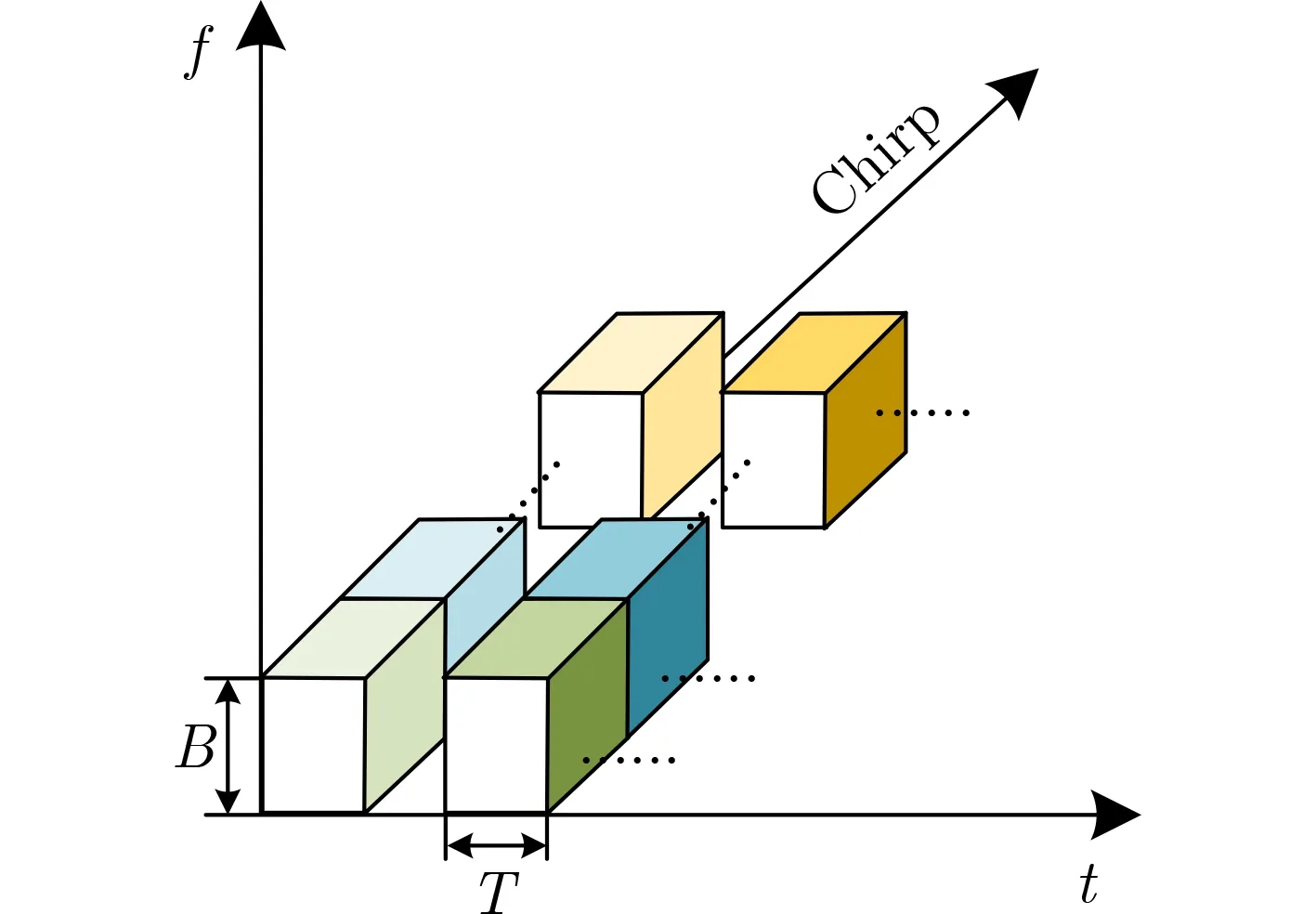
图1 数字实现的OCDM信号

Chirp信号的频率是线性的，相位随时间呈2次变化

x(l)是 第l个子载波上的符号，与菲涅尔变换获得的Chirp信号组合，表示OCDM信号。

OCDM信号通过离散菲涅尔变换实现，离散OCDM信号可以表示为

其中，ΦH是 IDFnT矩阵，x是调制符号，接收机可以通过DFnT恢复符号。

2.2 OCDM系统结构

在下面的推导过程中，N取偶数。根据式(2)，DFnT矩阵有式(7)形式

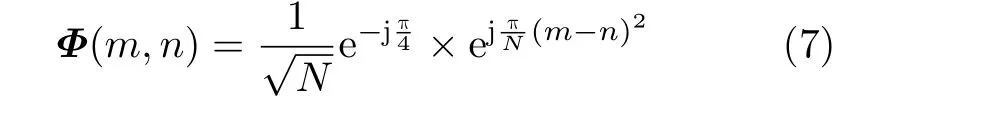
经典的DFT矩阵的表达式为

通过以上分析，结合OFDM系统结构，OCDM系统基带结构图如图2所示。

图2 OCDM系统基带结构图

在发射端，输入数据由串行转换为并行，并映射成通信符号。然后，将并行通信符号通过IDFnT矩阵，得到OCDM符号。添加循环前缀(Cyclic Prefix, CP)后，通过并行/串行转换将其传输至信道进行传输。在接收端，通过串行/并行变换，去除CP，通过DFnT矩阵恢复通信符号。最后，经过均衡、解映射和并行/串行转换，得到最终数据。通过和OFDM系统的比较，发现这两种系统的结构框架基本相似，主要区别在于符号调制方式。

传统的多载波技术，在频率选择性衰落信道中，可以通过简单的增益和相位的调整，对每个独立子信道中的失真进行补偿[11]。然而，在快衰落信道中，传统的傅里叶变换方法不适用，由于信道频率响应快且时变，许多传统的多载波系统失去了最佳性。因此，我们选择Chirp型正交信号作为基函数，其分析和合成方法可以与传统傅里叶变换复杂度相同。

2.3 信道模型

在这篇文章中，以时域循环矩阵H来描述信道模型。假设调制后的发送信号为s(n)，经过时变信道后的接收信号为y(n)，它们之间有式(9)关系：

其中

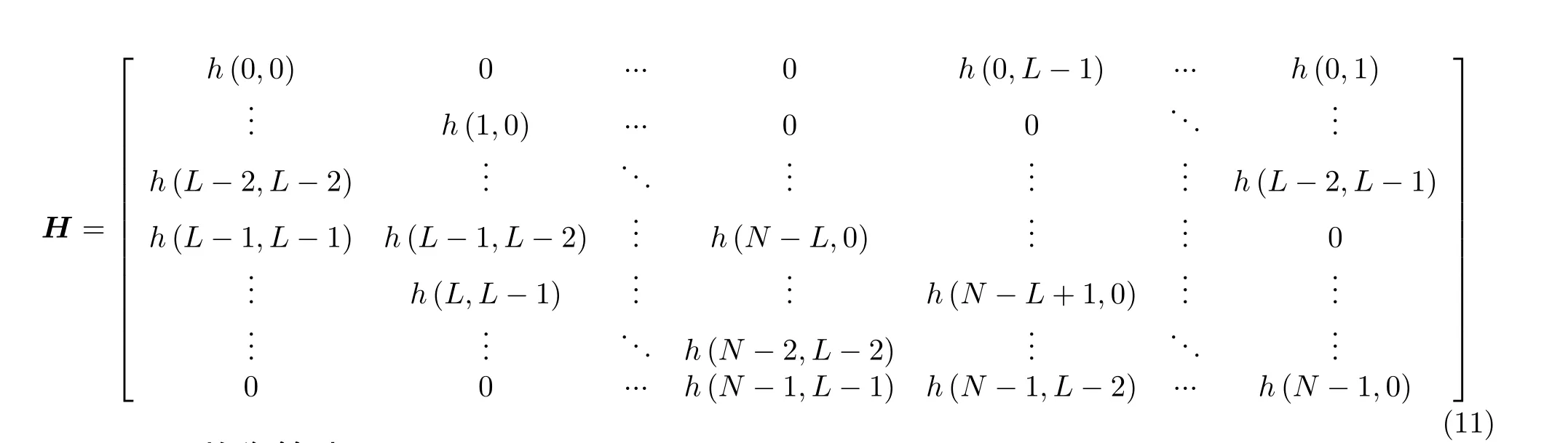
3 OCDM均衡算法

如2.2节所述，OCDM系统和OFDM系统有着相似的结构框架。因此，OFDM系统的常用的均衡方法，经过适当的改进之后可以用于OCDM系统之中，这一部分重点介绍应用于OCDM系统中的均衡算法。首先，介绍抵消相位的MMSE均衡算法(Minimum Mean Square Error-Offset Phase,MMSE-OP)，记作方法A。经过修正后的BDLSQR算法，记作方法B。在近似带状矩阵的基础之上，结合判决反馈均衡，提出了LSQR-BDFE算法，记作方法C，并给出结构图和详细的公式推导过程。

3.1 MMSE-OP算法

DFnT矩阵具有特征分解的特性，均衡过程可以对其进行相位抵消来降低复杂度。文献[4]中，使用了MMSE-OP算法，在频率选择性衰落信道中，这种方法十分简便。

根据式(5)和式(11)，接收端为

G表示均衡器，采用MMSE均衡时，GMMSE(k)=Λ∗(k)/|Λ(k)|2+ρ−1，ρ是SNR。

在双选信道下，频域信道矩阵不再对角，而是一个满元素的矩阵。此时，MMSE-OP算法的求逆过程变得十分复杂，为了降低复杂度，我们只考虑对角矩阵来进行频域均衡。

3.2 Band Damped-LSQR算法

多普勒频移对于信道的频率响应大部分集中在对角以及其附近，将信道的频域矩阵近似为带宽为Q的带状矩阵，Q表示由ICI导致的符号能量泄露宽度。LSQR算法是一种适合求解大型稀疏矩阵的最小二乘迭代方法，具有很大的优势，阻尼LSQR算法是考虑到实际系统中的噪声因素，对其进行的修正。结合以上两点，提出一种基于近似带状矩阵的阻尼LSQR算法，下面对BD-LSQR算法的实现过程进行推导。

首先，近似带状矩阵可以看作图3所示[14]。带状近似处理后的信道矩阵为

图3 近似带状矩阵图

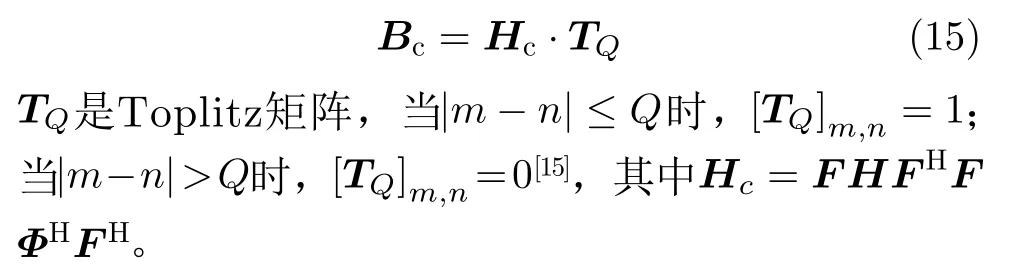
接下来，对LSQR算法的实现过程进行简单介绍，如式(12)所示，忽略噪声的影响，接收机和发射机之间可以形成一个线性系统。

迭代之后，实现最小残差的模为//Hsk −r//2。当迭代后的输出结果满足最小残差时，求解过程完成。否则，重置容差大小和迭代次数，将其输入式(17)中进行求解运算。

阻尼LSQR算法考虑到实际系统中的噪声因素，其接收机和发射机之间的关系和式(12)一致，MMSE均衡算法可以表示为

式(18)描述的是修正后的阻尼LSQR算法，构造出矩阵H′和向量r′

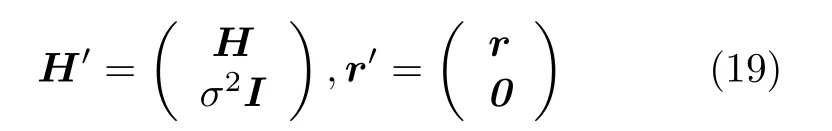
其中，参数σ2和 噪声n功率有关，信号功率为1时，等效为ρ−1，σ=0时，阻尼LSQR算法可以退化为LSQR算法。当进行频域均衡时，H可以进行带状矩阵近似，用Bc替换。

3.3 LSQR-BDFE算法

在方法B中，我们提出了BD-LSQR的均衡算法。在双选信道下，由于其带状矩阵的近似特性，表现出优于方法A的性能。为了进一步缓解快速时变信道中的ICI，在近似带状矩阵的基础上，结合判决反馈均衡，通过LSQR算法进行迭代计算，提出LSQR-BDFE算法。文献[17]中，提出了应用于OFDM系统中的LSQR-BDFE算法，它将LSQR算法与MMSE-DFE相结合，获得更好的性能。我们首次提出将LSQR-BDFE算法应用于OCDM系统中，下面给出该算法的推导过程。

关于近似带状矩阵的过程和LSQR算法的基本原理，在3.2节已经做了详细的推导和说明，这里不赘述。对OCDM系统中LSQR-BDFE均衡过程进行推导，BDFE的实现过程如下，其结构框图见图4。

图4 BDFE结构图

这种方法通过构造前馈滤波FF和反馈滤波器FB，使得误差e有式(20)形式：对式(24)进行LSQR求解运算，得到经过前馈滤波器FF的输出结果。

接下来进行判决反馈，需要注意的是，在判决反馈过程中，FB为严格的上三角矩阵，xˆF是数据估计值。假设数据估计的结果xˆF都是正确的，判决的顺序从第N个子载波到第1个子载波，将数据估计的xˆF经 过反馈滤波器FB，最后一列上进行加权计算，在y中将反馈后的结果减去，这样第N个子载波对其他子载波产生的ICI可以去除。接下来对第N−1个子载波上的数据进行检测，重复上述过程，最终得到所有子载波的反馈结果后输出。

4 性能分析

4.1 复杂度分析

对第3节所述3种均衡算法的复杂度进行简要分析。

方法A的MMSE-OP算法，DFnT是由DFT矩阵附加2个相位变化得到的，复杂度为N2，抵消相位避免了DFnT运算过程。单抽头MMSE均衡的复杂度为N[18]，FFT和IFFT的复杂度为Nlog2N，均衡过程需要1次FFT和IFFT运算，总复杂度为N+2Nlog2N。

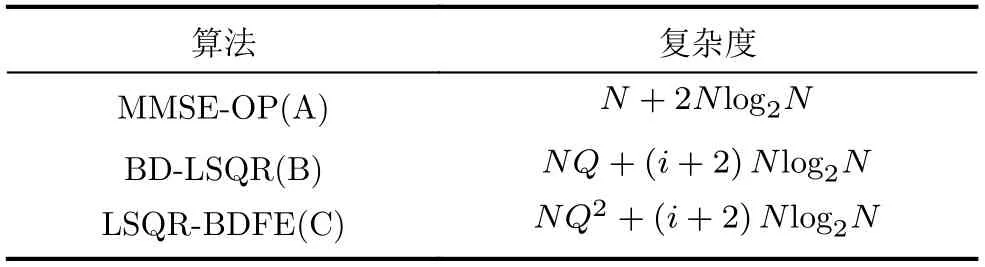
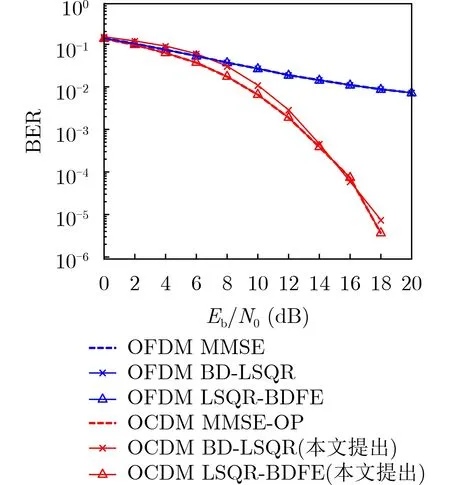
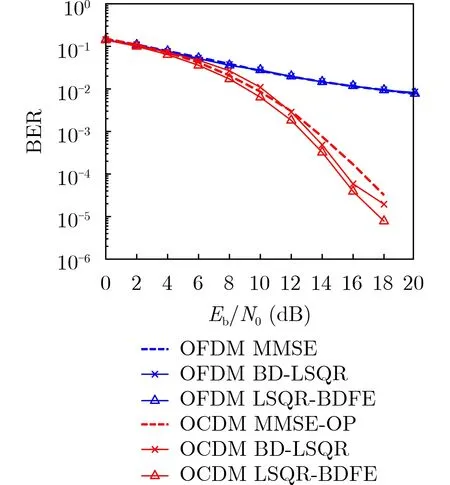
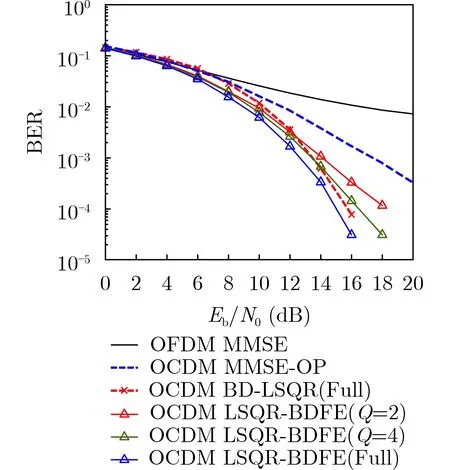
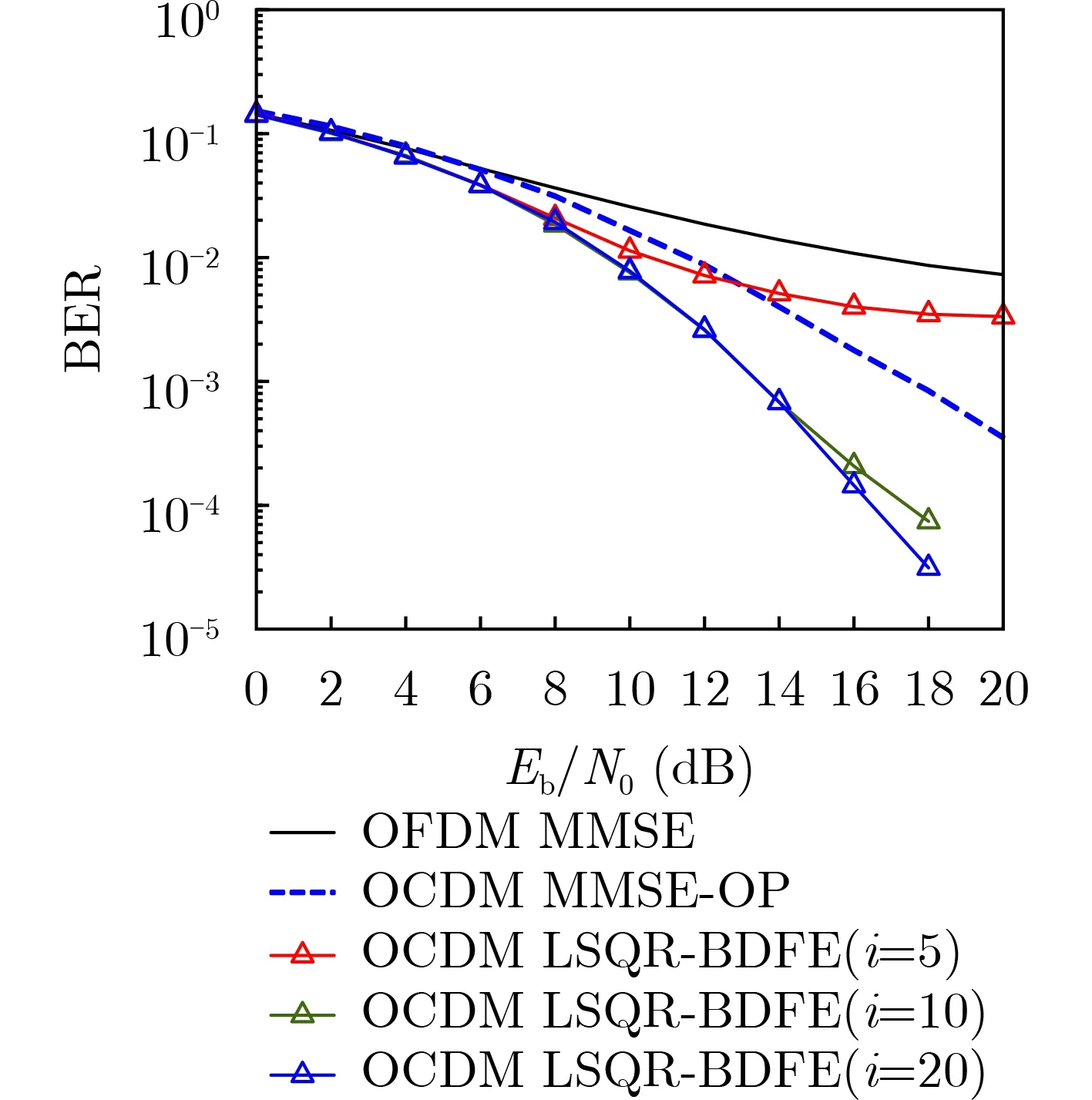
方法B的BD-LSQR算法，近似带状矩阵过程的复杂度与带宽Q有关[19]。Damped-LSQR算法的复杂度与子载波个数N和迭代次数i有关[20]，其中i

从表1可以看出，3种均衡算法的复杂度与N均为线性关系，具有低复杂度的特性。

表1 3种均衡算法的计算复杂度

4.2 BER性能曲线

在OCDM系统中，考虑子载波个数N=128，采用QAM映射，每个OCDM符号携带256 bit信息。多径衰落信道的参数为时延delay=[0 3 15 3137 51 71 73 109] ns，相对功率pdb=[0 –1.5 –1.4–3.6 –0.6 –9.1 –7.0 –12.0 –16.9] dB，此模型为EVA信道模型。

在多径信道下，频域信道矩阵为对角矩阵，近似带状矩阵和频域矩阵相同，此时3种均衡方法的BER性能基本一致。由于OCDM信号可以有效地利用多径分集，表现出比OFDM信号更强的抗衰落能力[5]，如图5所示。

图5 多径信道下OCDM系统和OFDM系统BER曲线图

在高速移动的场景下，以归一化频移fd=0.08加入，3种均衡算法的BER曲线如图6所示。随着信噪比的提高，在OFDM系统中，单抽头MMSE均衡算法和LSQR算法会出现误差下限[17]。取带状近似矩阵Q=4，LSQR-BDFE算法中迭代次数i=20。可以看出，在OCDM系统中，方法B和方法C相比方法A，有着更好的性能。

图6 双选信道下OCDM系统和OFDM系统BER曲线图(f d =0.08)

图7为归一化频移fd=0.16时，OCDM系统中3种不同均衡算法的BER曲线。当信道的时变衰落增加时，方法A的性能变差，取带状近似矩阵Q=2和Q=4，和不做近似的信道矩阵3种情况作比较，迭代次数i=20。可以看出，方法B和方法C相比于方法A来说，具有一定的性能优势。随着Q值增大，对于信道信息的还原也更准确，BER性能提升。

图7 双选信道下OCDM系统BER曲线图(f d =0.16)

最后，比较LSQR算法的不同迭代次数对于BER性能的影响，以方法C的LSQR-BDFE算法为例，取带状近似矩阵Q=4，迭代次数分别为5,10和20次，如图8所示。当i=5时，方法C的BER性能不如方法A，此时LSQR算法的迭代次数较少，不满足求解的最小残差值，因而误差较大；随着迭代次数i的增加，其性能有着明显的提升。

图8 不同迭代次数下的BER曲线图

5 结束语

本文以OCDM系统为框架，重点研究了OCDM系统的低复杂度均衡算法。针对双选信道下，传统MMSE均衡算法性能下降的现象，提出带状阻尼LSQR算法。为了缓解时变信道中的ICI，提出LSQR-BDFE算法，并给出两种算法的公式推导过程。最终，通过复杂度分析和BER性能曲线，验证了所提出的带状阻尼LSQR算法和LSQR-BDFE算法，相比于现有的MMSE均衡算法的性能优势。基于菲涅尔变换的OCDM系统，和OFDM系统相比，有着更强的抗衰落能力，因此OCDM系统具有广泛的应用前景和价值。