基于自然梯度Actor-Critic强化学习的卫星边缘网络服务功能链部署方法

高 媛 方 海 赵 扬 杨 旭

(西安空间无线电技术研究所 西安 710100)

1 引言

6G空天地一体化网络愿景将低轨卫星网络纳入其中，以实现全球覆盖，满足更可靠、广泛、灵活和安全连续的服务需求。为适应未来星地网络发展，新一代卫星载荷将采用星载动态可重构架构，以及软件化和智能化技术，以实现资源虚拟化和网络动态调度[1]。而低轨卫星网络将面临星上资源及计算能力有限等挑战。为将有限的计算、存储和通信等资源充分利用，文献[2]提出了一种云边端一体化协同网络架构，在低轨卫星集群上部署边缘云；通过人工智能、分布式信息网络和星载可重构架构等一系列技术，将软硬件基础设施资源云化，从而实现任务的分布式管理。

目前，对卫星边缘云的研究尚处在初步阶段。文献[3]梳理了近年来低轨卫星通信网络的进展历程，首先对多接入边缘计算(Multi-access Edge Computing, MEC)在天地融合网络中的应用进行了分析，然后提出了低轨卫星MEC网络的组网方式，最后对该网络架构所面临的挑战与机遇进行了总结。须指出，随着6G应用场景的扩展，卫星业务呈现出高并发以及种类多样性等特点，云边端一体化协同网络将面临如何为不同类型的业务提供定制化服务，以及如何实现资源的智能动态协同适配等挑战。而文献[4–6]则提出，将软件定义网络(Software-Defined Networking, SDN)和网络功能虚拟化(Network Function Virtualization, NFV)与云边端架构相结合，可将任务编排为多个虚拟网络功能(Virtual Network Function, VNF)的有序组合，用逻辑链路的方式合成为一条服务功能链(Service Function Chain, SFC)，引导业务流依序通过，从而具备提升网络资源利用率的潜力。

然而，鉴于卫星网络的高动态性及星地环境的复杂性，卫星边缘云节点无法与地面云控制中心实时联通；因此，卫星边缘云须具备自主控制和自主智能决策能力，以自主执行服务部署和服务迁移。因此，如何设计SFC编排与映射方案，以提升资源利用率并优化服务质量，实现在线智能的快速响应，构成卫星边缘云一个重要的研究内容[7]。

与地面蜂窝网络不同，卫星边缘网络资源受限且节点快速移动，与地面中心云间的通信成本高、时延大。因此，在自主管理模式下，卫星边缘云能够以就近可通原则形成卫星集群，簇头卫星节点充当临时管理者，收集局部网络资源信息并将资源池化管理，从而具备了自主控制能力。进一步，针对临近卫星节点发送的任务请求信息，中心节点可结合当前网络的拓扑实时信息，对网络拓扑中的流量路由和虚拟化资源进行灵活调度，从而依照不同服务请求，实现对SFC的动态编排和映射。此外，在大延迟抖动、间歇联通和周期移动切换等场景中，当发生运行VNF的卫星节点失联等情况时，卫星边缘网络须根据实时网络状态进行服务迁移，由中心节点担任自主迁移的决策者[2]。

目前，针对SFC部署的研究主要集中在地面网络。文献[8]针对在高速变化的5G网络资源状态下进行SFC部署的复杂度较高等问题，提出利用深度Q网络的方法进行在线求解，在满足服务的端到端时延需求等约束下，最小化系统开销。同样基于强化学习和地面网络，文献[9]首先建立了VNF和虚拟链路的可靠映射模型；其次，以负载均衡和VNF可靠性为联合优化目标，在线学习最优SFC部署策略。此外，面向卫星网络，文献[10]考虑了低轨、中轨和高轨卫星共存的网络场景，针对多域(multi-domain)和卫星自组成(satellite formation)两种模式，分别提出启发式的部署算法。文献[11]将空间信息网络建模为时间扩展图(Time-Expanded Graph, TEG)，进而将SFC部署表征为线性约束的最大流路由问题，并利用基于图论的启发式算法求解。

综上所述，目前已有的研究低轨卫星网络SFC部署的工作往往研究单时隙中服务功能(Service Function, SF)向卫星节点的VNF实例的映射问题[10–12]。然而，低轨卫星网络的运行和资源管理是一个长期过程，可用资源和网络环境随机变化；若只考虑单时隙SFC部署，即逐时隙利用贪婪策略做资源分配，则无法保障网络的长期奖励(性能)最大化。例如，鉴于低轨卫星网络的高动态性和空间环境的复杂性，两个相邻时隙的SFC部署结果不同，则导致快速变化的SFC路由拓扑，从而导致SFC服务(包括状态信息和数据流)迁移代价的增大[13]。因此，单时隙SFC部署方案没有考虑低轨卫星网络的动态特性，无法获得最优的长期收益。

因此，考虑低轨卫星网络的高动态性和空间环境的复杂性，如何提供在线的快速SFC部署方法，并综合考虑节点和链路容量等约束以及服务迁移等代价，成为低轨卫星边缘网络中亟待解决的问题。无模型(model free)强化学习可将系统动态建模为一个马尔可夫决策过程(Markov Decision Process,MDP)，尽管相邻时隙之间的状态转移概率是未知的，但通过在线决策和连续采样，可获取即时奖励值来评价当前状态的价值函数，最终得到长期最优的连续SFC部署策略。从而，本文拟提出一种基于参与者-评价者(Actor-Critic)强化学习的卫星边缘网络在线SFC部署方法。首先，针对低轨卫星网络的高动态性，对容量约束和迁移代价进行定义，并对长期SFC部署问题进行建模。其次，引入MDP，综合考虑服务迁移和卫星坐标等因素，对系统状态、动作和奖励函数进行定义，描述低轨卫星网络的状态转移过程。再次，提出一种基于自然梯度(natural gradient)法的在线强化学习部署方法，以最小化服务请求的平均端到端时延为优化目标；与标准梯度(standard gradient)法中对参数进行迭代更新不同，自然梯度法进行模型层面的更新，从而避免出现模型更新不均匀的现象，保障模型收敛到全局最优解。最后，仿真结果表明，本文方法在满足节点容量和服务迁移代价等约束条件下，可最小化SFC的平均端到端时延，逼近长期平均策略函数的全局最优值。

2 系统模型和问题描述

利用NFV技术，每个卫星节点服务器可被虚拟化为多个虚拟机(Virtual Machine, VM)，并假设每个VM只能提供一个VNF实例。本文研究一个卫星集群内的SFC部署以及SF到VNF实例的映射，资源分配决策由集群内中心节点卫星负责，如图1所示。考虑一个虚拟化的边缘低轨卫星网络，卫星节点集合可表示为N={1,2,..., N}，并用n表示节点的索引值。此外，用F={1,2,..., F}表示该集群内所有节点可提供的VNF实例集合。同时，假设SFC部署的时间尺度小于VNF实例化的时间尺度，即本文假设在VNF部署已完成的基础上，拟完成SF到VNF实例的映射。最后，考虑一个动态低轨卫星网络系统，用T={0,..., t,..., T −1}表示时隙化的时间范围，并用t表示时隙的索引值。

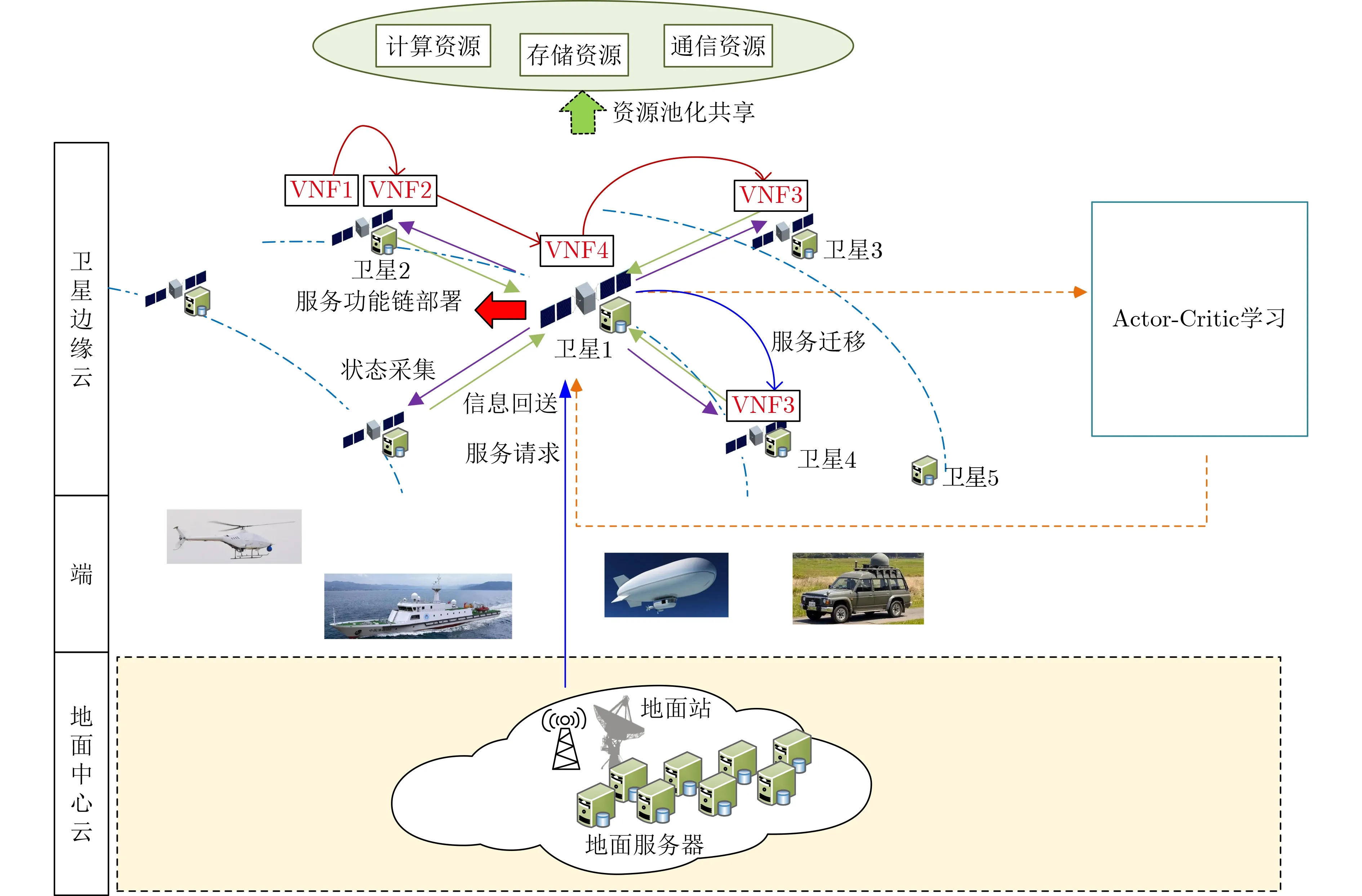
图1 SFC部署和迁移示意图

2.1 服务功能链和容量约束

基于SFC技术，低轨卫星网络中的每个服务请求均被映射为一个业务流，该业务流被SFC中的一系列SF依序访问。 因此，与服务请求i相关联的SFC可表示为

2.2 端到端时延

对于每一条SFC，其端到端时延可定义为在卫星服务器上的处理时延和卫星之间链路时延之和。首先，在每个VNF实例上，根据M/M/1模型[13]，对SFCi的每个分组的处理时延可计算为

2.3 服务迁移代价

2.4 问题描述

本文旨在最小化所有服务请求在时间范围T内的分组平均端到端时延，即

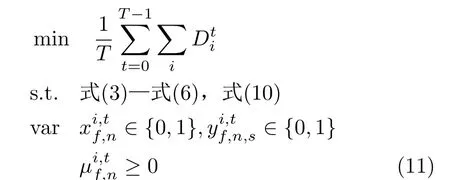
特定地，令T=1，则式(11)简化为一个单时隙SFC部署问题，该问题已被证明是一个NP难问题[15]；因此，式(11)同样构成一个NP难问题，其未来系统状态信息是未知的，难以用离线算法或动态规划等方法求解。然而，经观察，式(11)是一个具有MDP性质的动态部署问题，可利用无模型的强化学习框架，逐时隙在线学习不同状态下的最优部署动作，以实现最大化卫星边缘网络长期奖励的目的。在第3节中，本文将采用强化学习中的Actor-Critic网络框架，在线学习长期最优的SFC部署策略。

3 基于自然梯度Actor-Critic架构的SFC部署方法

Actor-Critic框架被广泛应用于实际强化学习过程中，该框架集成了Q值函数估计算法和策略搜索算法。Actor网络根据参数化策略函数生成符合当前状态的动作，而Critic网络将状态-动作对映射到Q值，从而获得比传统的Q学习更高的训练效率。本文Actor-Critic算法框架采用自然梯度对模型进行更新：与标准梯度法中对参数进行迭代更新不同，自然梯度法进行模型层面的更新，从而避免出现模型更新不均匀的现象。

3.1 马尔可夫决策过程

在长期优化问题中，智能体观测到的状态部分是随机的，部分依赖于智能体采取的动作。因此，MDP可用于状态具有马尔可夫性质的系统环境中，以模拟智能体可实现的随机性策略与奖励。本文将MDP建模为一个4元组(S,A,P,R)， 其中，S表示状态集合，A表示动作集合，P表示状态转移概率，而R:S×A表示即时奖励。此外，本文做了两个关键假设，即：智能体对环境具有完备的感知能力，且当前状态排除了任何不确定性。

其次，本文设计的即时奖励函数并不能由一个闭式表达式直接给出，而是须求解如下优化问题

3.2 Critic网络训练

首先，DNN作为一个监督学习模型，要求样本服从独立同分布。因此，通过存储智能体的经验值，基于存储采样的回放技术将构建一个经验回放池。经验回放池将以4元组的形式存储每一条样本，随后DNN会随机抽取一批样本进行批量训练，从而打破了样本之间的时间相关性。

然后，在每次迭代中，由于DNN参数值是即时更新的，DNN的目标值也在同步变化。若将不断变化的目标值用于参数训练中，则Q值的估计值很难趋于稳定。因此，须利用双神经网络技术，构建一个额外的目标DNN；与原网络进行实时更新不同，目标网络的更新频率较低，其将一直保持参数不变，直到固定的更新时刻才进行参数更新，并将原网络的模型直接赋予到目标网络中。双神经网络技术可有效避免训练过程中的参数发散。至此，可将Q函数的估计值和期望值之差的损失函数设计为

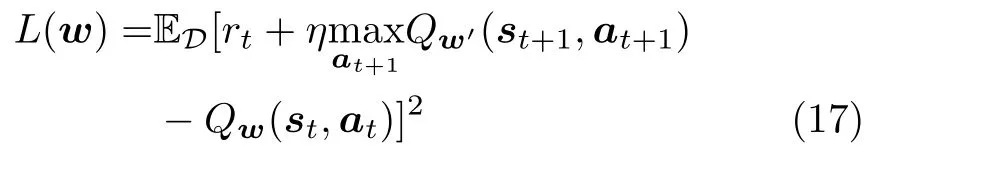
式(20)表示利用不同样本计算得出梯度信息的平均值，然后再用平均值来调整该DNN的参数。具体地，D表示从经验回放池中抽取得到的样本个数，d表示样本序号，而αc表示Critic网络的学习率(步长)。

3.3 Actor网络训练

Actor网络使用策略函数来生成动作并和环境交互；而Critic网络使用DNN去近似Q值函数，以负责评估Actor的表现，并指导Actor下一时隙的动作。因此，在Actor网络中，若将参数设为θ，则策略函数π可近似为

其中，p(·)表示所有状态的初始概率分布。

须指出，在传统的梯度法中，J(πθ) 和πθ均采用欧氏距离去衡量参数值的变化，例如：参数更新值∆θ可 用L2范数| |∆θ||2来衡量。然而，文献[16,17]已证明，不同于参数，策略难以用欧氏距离来准确衡量，即：在参数空间中距离相等的任意两对参数，其对应策略可能相差很大，也可能相差很小。因此，本文将采用自然梯度法，在保持| |∆θ||2不变和减少迭代次数的前提下，使得J(πθ+∆θ)最大。

首先，利用平均Kullback-Leibler(KL)散度来衡量两个模型之间的策略距离，即

3.4 基于自然梯度的Actor-Critic学习算法

综合3.2节和3.3节，可得到基于自然梯度的Actor-Critic强化学习的卫星边缘网络SFC部署算法，如算法1所示。

须指出，算法1利用式(27)中的自然策略梯度对Actor参数进行更新，可改善训练稳定性，增大收敛速率，并保障期望奖励值收敛到某个驻点[18,19]。

算法1 基于自然梯度的Actor-Critic算法

4 仿真结果与分析

4.1 实验环境和参数设置

本实验在仿真服务器上进行，配置如下：4个NVIDIA GTX 1650 GPU，1个锐龙5 3600 6核处理器和1个128 GB内存，软件环境为TensorFlow 1.14.0, Python 3.7.1和MATLAB R2021a。

为仿真低轨卫星拓扑，本实验采用MATLAB R2021a推出的卫星通信工具箱。采用极轨星座(每轨24颗卫星，共30条轨道)，轨道高度为343.164 km，偏心率为0，轨道倾角为90°，右旋升交点赤经在0～180°内均匀采样，间隔为6°，真近点角在0～360°内均匀采样，间隔为15°[20]。为减小仿真负荷，本文只考虑了相邻4条低轨卫星轨道，每条轨道上卫星数目为2～8。此外，令每个服务请求的分组到达率为200 packets/s，每个卫星节点的处理容量服从500～1000 packets/s的均匀分布，每个服务请求的数据率需求设置为1 mbps，且相邻两条轨道上任意两个卫星节点的链路容量服从10～20 mbps的均匀分布。最后，将任一SF的迁移代价统一设置为1，且将每时隙内的迁移门限值设为20。

在搭建Actor网络时，将隐藏层和输出层的激活函数分别设置为ReLU和Softmax函数。此外，设置两个隐藏层，每层50个神经元，折扣率设为0.9，经验回放池大小设为32；同时，采用ε贪婪策略，贪婪系数为0.9；最后，将最大回合数设为100，且每回合内迭代次数设为200。

4.2 性能分析

为验证算法1的性能，本文对比分析了文献[14]中的在线SFC映射算法，即基于正则化的分数阶算法(Online Regularization-based Fractional Algorithm, ORFA)，以及文献[8]中的基于深度Q网络的服务功能链部署(Deep Q Network-based Service Chain Deployment, DeepSCD)方法。须指出，ORFA和DeepSCD算法均是在满足时延约束的前提下，最小化计算和通信资源开销。同时，为比较自然梯度和标准梯度，将这两种梯度方法分别记为Natural Actor-Critic(NAC)和Standard Actor-Critic(SAC)。

图2显示了本文方法(NAC)在不同学习率和样本批量设置下的每学习回合内的时间平均奖励，并设服务请求个数为6，卫星节点数为4 ×3，每条SFC中SF个数为4。图2(a)中，学习率分别设置为0.001，0.0005，0.0001，0.00005和0.00001。从图2(a)可看出，首先，学习率设置在算法训练阶段会直接影响奖励值的大小。其次，学习率过大会导致梯度迭代时的步长过大，错过全局最优解，从而陷入局部最优解或鞍点；而较小的学习率导致步长过小，逼近最优解的收敛速率较慢。其中，0.0001学习率表现出较好性能，不仅能获得最大平均奖励值，而且收敛速率较快；而0.001学习率性能最差，尽管在第10轮学习回合左右开始收敛，但陷入了一个局部最优解。图2(b)描述了样本批量大小对本文方法收敛性能的影响，批量大小分别设为4，8和16。如图2(b)所示，样本批量大小将影响训练阶段奖励函数的收敛速率。样本批量过小可能导致较大方差，使得收敛速率较慢甚至不收敛。反之，样本批量较大时，梯度估计值更加稳定和准确，但需要较长计算时间，且可能导致神经网络陷入局部最优解。特定地，在样本批量大小为8时，平均奖励在第10轮回合时开始收敛，且获得最大奖励值。因此，以下实验均将学习率大小设为0.0001，批量大小设为8。

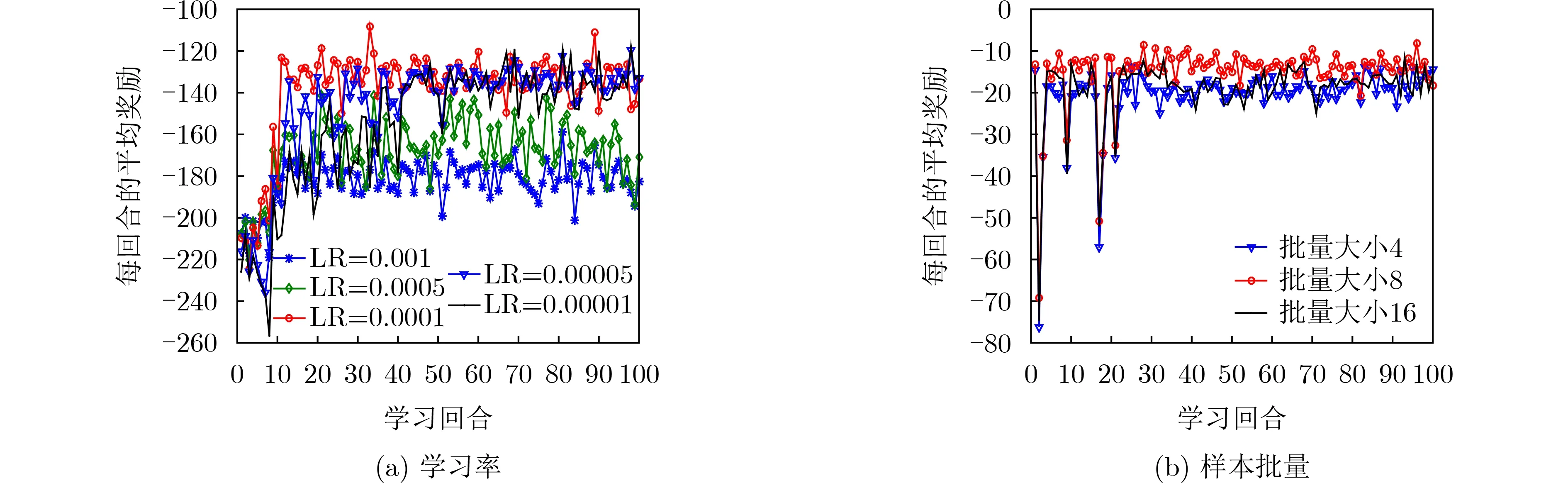
图2 不同学习率和样本批量大小对平均奖励函数的影响

图3表示了不同服务请求个数下，所有SFC的端到端时延和在一个回合内的时间平均值。每条SFC中的SF个数设置为4，卫星节点数为4× 3。如图3(a)所示，当请求数等于9时，所有算法的可行解比例下降到60%左右，并且在请求数等于8时迅速攀升至90%以上。这是因为：当SFC数量增加时，剩余资源和可用容量将趋于饱和，无法为所有SFC提供可行的映射结果。而图3(b)表示，随着SFC条数的增加，NAC方法始终获得最低的时延，并且在SFC数目较低时，4种算法的性能相近。这是因为：SFC数目较低时网络资源较为充分，可为所有的SFC提供最短路由路径。此外，通过计算所有服务请求的总时延值大小，可知相较其它3种算法，NAC方法的时延平均值分别低7.8%, 10.1%和12.3%。

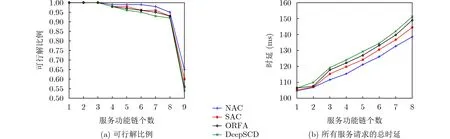
图3 不同服务请求个数对端到端时延性能的影响

图4表示在不同SF数目设置下算法的时延性能比较。此时，将SFC个数设为4。如图4所示，首先，随着SF的增多，卫星节点的处理时延，以及卫星链路之间的传播时延均会增大，从而导致每条SFC的端到端时延增大。此外，NAC方法总是具有最低的总时延，并且能在一定数值范围内保持相对稳定；然而，当SF数接近10时，随着非可行解的增多，NAC方法的总时延也迅速增大。相较其它3种算法，NAC方法的时延平均值分别低7.1%,15.7%和20.1%。

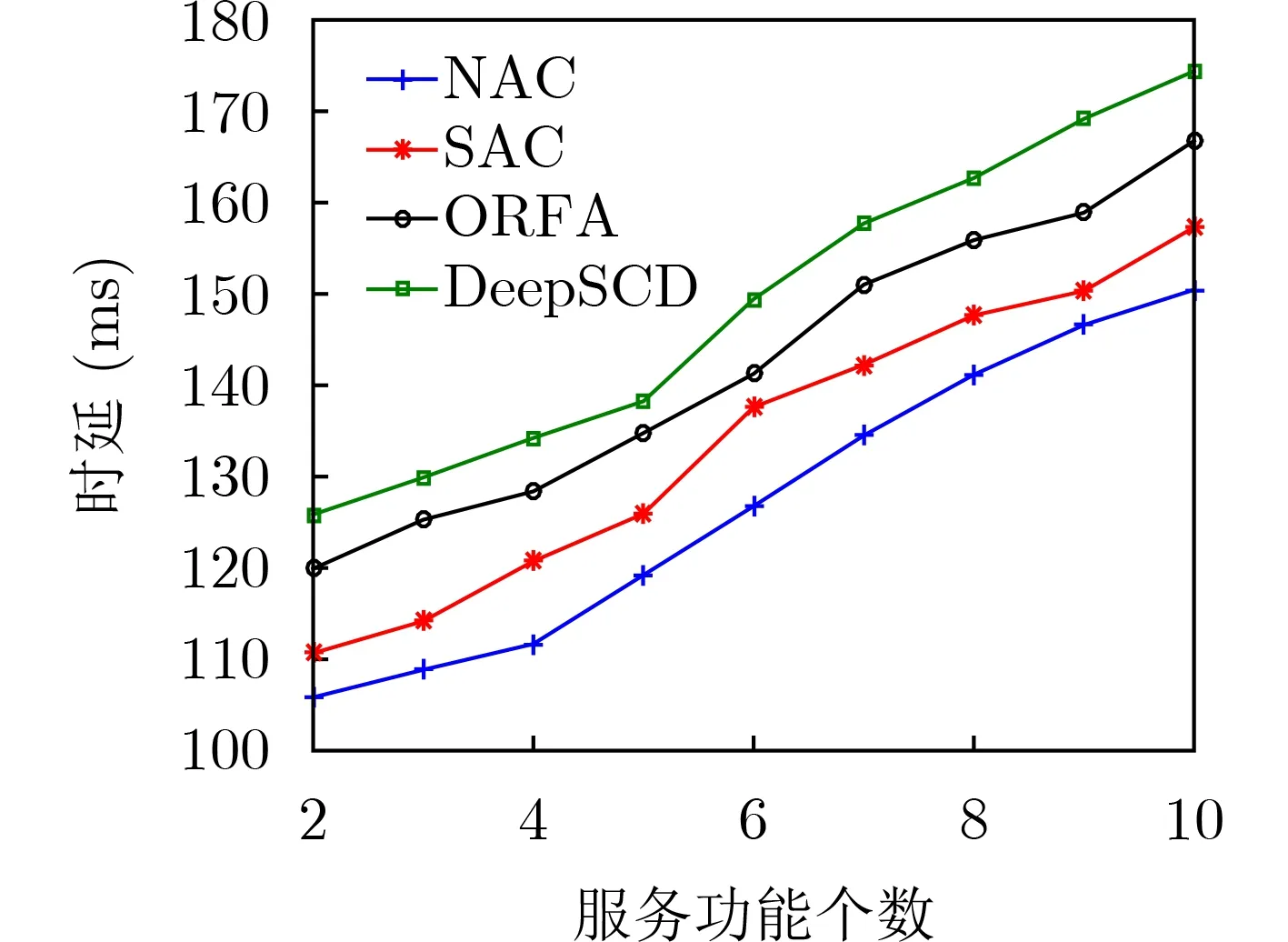
图4 每条SFC内不同SF个数对端到端时延性能的影响

图5表示在不同低轨卫星节点数设置下算法的性能比较，将SFC个数设为5，每条SFC中的SF个数设为4，轨道数设为4。如图5所示，随着卫星节点数的增大，可用计算资源也逐渐增多，SFC路由路径更加灵活，从而获得更低的端到端SFC时延。

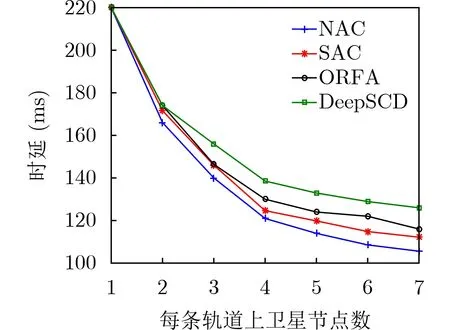
图5 每条极地轨道上卫星节点个数对端到端时延性能的影响

5 结束语

本文研究了基于自然梯度的Actor-Critic强化学习方法在低轨卫星网络SFC部署问题中的应用。与标准梯度法不同，自然梯度法在非凸神经网络训练中可获得更高收敛速率，且不易陷入局部最优解。同时，本文研究了SFC部署中的服务迁移问题，通过考察连续两个时隙的分配变量，将服务迁移代价建模为一个凸约束问题。此外，为降低动作空间大小，本文采取了一种基于子优化问题的奖励函数计算方法。最后，实验验证了本文提出方法的有效性，其具有较高收敛速率，且在端到端时延性能上优于已有方法。