新型立柱储油式半潜平台水动力特性频域分析

陶路舒，赵 波，曹颜玉，李 云，高秀峰

（1.西安交通大学，西安 710049；2.海洋石油工程股份有限公司特种设备分公司，天津 300451）

0 引 言

随着海上油气工业向深水和超深水发展，半潜式平台等浮式系统在油气开采中发挥着越来越重要的作用[1-2]。与固定的海上平台相比，浮式系统中使用的设备在结构的运动响应方面具有非常严格的要求，运动响应已经成为浮式系统设计的关键标准。特别是在垂荡方向上[3]，必须重视浮式系统的水动力性能和运动响应。

为适应更高的工作要求，我国设计建造了世界上首座具有凝析油储存和动力定位穿梭油轮外输功能的半潜式生产平台，如图1 所示，该平台配备有可以储存约20 000 m3（145 000 t）凝析油的立柱式储油舱[4]。储油式半潜平台既能够提升半潜平台的稳定性，也能为外输凝析油提供一定的存储空间。

该半潜平台在油气生产过程中存储的凝析油会排空，储油舱液位高度变化可达40 余米，这使平台的吃水、质量、惯性半径等会随储油量变化而发生改变，因此其水动力特性与运动响应特点相较于传统的半潜平台更为复杂。

学者们在半潜平台水动力变化规律方面做出了许多研究。Zhu 等[5]基于转向质量阻尼器系统的原理，通过迭代计算研究了垂荡板对半潜平台升沉运动的抑制作用；Song 等[6]在时域与频域两方面对两种不同立柱结构的半潜平台进行了全面的水动力研究；Ding等[7]在三维数值波浪水槽中研究了由不同角度的内部孤立波传播引起的半潜式平台周围的水动力和流场特性；苗玉基等[8]采用势流理论对两模块半潜平台波浪漂移力进行了频域分析。上述研究所涉及的半潜平台均不具备大容量储卸油能力，这使得在半潜平台水动力领域缺乏对储油量因素影响的研究。

为掌握这种新型平台的水动力特性与响应特点，本文建立了考虑储油量变化的新型立柱储油式半潜平台的水动力模型。鉴于频域分析可以较为全面地反映半潜平台水动力特性，且为时域响应预测的基础[9-11]，本文重点研究了在变储油量工况下其频域水动力特性。

1 储油式半潜平台水动力建模

1.1 储油式半潜平台结构与坐标系

储油式半潜平台由下部浮体、立柱与甲板组成，如图1（a）所示。在四个立柱内部均布置有凝析油储存舱，在浮体的四角内布置有调载压载舱，通过吸入与排出海水调整半潜平台吃水，如图1（b）所示。当半潜平台排出凝析油时，压载舱吸入海水；当半潜平台载满凝析油时，压载舱排空。

图1 新型立柱储油式半潜平台Fig.1 New type of column oil storage semi-submersible platform

半潜平台坐标系设置如图2（a）所示，采用笛卡尔坐标系OXYZ作为参考坐标系，Z轴竖直向上且坐标系为右手系。同时建立随体坐标系oxyz，设定浮体重心G与坐标原点o重合，初始状态下其坐标轴与参考坐标系OXYZ的各轴平行，如图2（b）所示，其中β为入射波传播方向与OX轴正向的夹角。

图2 半潜平台坐标系示意图Fig.2 Schematic diagram of semi-submersible platform coordinate system

1.2 半潜平台船体部分的水动力载荷

三维势流理论是当前分析船舶水动力特性最成熟的理论之一，其主要考虑波浪载荷对结构的绕射效应和辐射效应，适用于大尺度海洋结构的波浪载荷计算，半潜平台船体部分的水动力载荷计算多采用该理论[12]。根据叠加原理，流场中的速度势Φ可分解为入射势ΦI、绕射势ΦD以及辐射势ΦR，每一项均满足流体域内的拉普拉斯方程，并且受相应边界条件的约束[13]，有

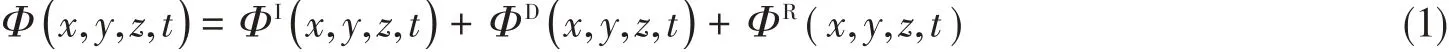
储油式半潜平台一阶水动力荷载由两部分组成：波浪激振力和辐射力。根据线性化的伯努利方程，一阶波浪力表达式[14]为

式中，s0是半潜平台的平均湿表面，ρ是水的密度，ΦI和ΦD分别是入射势和散射势的空间分量，（j=1，2，…，6）是第j个自由度单位振幅辐射势的空间分量，nj（j=1，2，…，6）是垂直于物体表面的方向朝外的单位法向量。

波浪激振力是与入射势有关的Froude-Krylov力和与散射势有关的散射力之和。而辐射势产生的辐射力可进一步用附加质量和辐射阻尼表示，

式中：FRjk是由第j个运动模式引起的第k个自由度的辐射力或力矩；和分别是强迫运动的结构线性运动速度矢量和加速度矢量；μkj与λkj分别是半潜平台的附加质量和辐射阻尼，它们通常与频率有关，且满足以下关系：

1.3 频域运动方程

波浪频率与波向角对结构物的水动力性能有显著影响，应用牛顿定律，可以通过以下频域运动方程确定储油式半潜平台响应矢量X(ω,β)[14]：

式中：M是平台的质量矩阵，由储油质量、压载质量与平台质量构成；附加质量矩阵μ由辐射势产生；λ(ω)是与频率相关的辐射阻尼矩阵；Bv是线性化的粘性阻尼矩阵；K和Ke是静水刚度矩阵与系泊系统的外部恢复矩阵；X(ω,β)为响应矢量，F(ω,β)为激振力矢量，与波频ω和波向角β有关。

2 储油式半潜平台模型尺寸

根据三维势流理论建立储油式半潜平台的湿表面模型，网格数为6878，如图3所示，表1给出了储油式半潜平台空载与满载时的主要参数。

表1 储油式半潜平台主要参数Tab.1 Key parameters of the semi-submersible platform

图3 半潜平台三维模型与水动力模型Fig.3 Three-dimensional model and hydrodynamic model of semi-submersible platform

由于半潜平台在风浪中摆动幅度较小[15-16]，因此在本文中认为凝析油液面不发生侧倾，而仅产生储存的凝析油的高度以及压载水高度的变化。为了在保证一定分析精度的同时节约计算时间，将凝析油与压载水的存储量进行十等分后建立了11个质量模型，并分别计算了在这11种状态下横摇、横荡与垂荡方向的频域水动力参数。

3 计算结果及讨论

3.1 质量特性

图4 质量特性Fig.4 Mass characteristics

惯性张量越大，船体越不容易发生翻转。图4（a）～（b）分别为半潜平台绕X、Y与Z轴三个方向上的惯性张量与惯性半径随储油量变化的曲线，平台的惯性张量随储油量增加而增大，绕Z轴的惯性张量变化趋势最为明显，满载状态的kzz值大约比空载时高出10%；惯性半径却没有呈现同样的规律，这是因为储油量增加引起的半潜平台质量分布变化较小，例如从空载状态到满载状态，绕Z轴的惯性半径变化仅为0.4 m。

3.2 一阶波浪力

作用在固定平台上的波浪激振力和平台强迫简谐运动产生的辐射力的合力称为船舶波浪载荷，通常用线性化一阶波浪力来表示。在本节中对0°入射角下该平台三个自由度的一阶波浪力进行了研究。

如图5（a）所示，图中横坐标是规则波的频率，纵坐标是一阶波浪力的幅值。随着规则波频率的增加，横荡一阶波浪力呈现出两个峰值，主峰频率为0.07 Hz，次峰频率为0.14 Hz。在所计算的所有频率下，横荡一阶波浪力皆随储油量的增加而增加，由图5（b）可以看出，在0.07 Hz处满载横荡一阶波浪力相比于空载增多了1600 kN/m。这是因为波浪激振力与水流方向垂直的横截面积成比例，储油量的增加会加深平台吃水，导致波浪入射方向的立柱截面积增大。图6（a）显示随着波浪频率的增加，垂荡一阶波浪力表现出两个峰值，主峰频率为0.08 Hz，次峰频率为0.16 Hz，且主峰与次峰幅值相差较大，这说明垂荡一阶波浪力能量主要集中在0.08 Hz附近。与横荡一阶波浪力相反，垂荡一阶波浪力在所有计算频率下均表现出随储油量增加而减小的规律，在0.08 Hz附近其斜率约为-125（N/m）/t，如图6（b）所示。这是因为在垂荡方向上并未发生截面积变化，而立柱浸入水中的部分长径比变大，导致等效质量系数的减小，从而波浪激振力减小。由图7可以看出横摇一阶波浪力受频率影响明显，在0～0.13 Hz区间内，横摇一阶波浪力随储油量的增加而降低，特别是在频率0.12 Hz处，其表现出非常明显的下降趋势，横摇满载一阶波浪力相比于空载降低了5×107°/m。在0.13 Hz 以后，横摇一阶波浪力随储油量的增加而增大。

图5 横荡一阶波浪力Fig.5 Sway first-order wave force

图6 垂荡一阶波浪力Fig.6 Heave first-order wave force

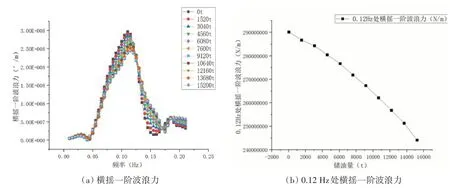
图7 横摇一阶波浪力Fig.7 Roll first-order wave force

3.3 辐射阻尼与附加质量

当半潜平台在静水中发生强迫谐波运动时，产生的辐射波会对平台产生辐射载荷，可由辐射阻尼、附加质量表征。它们与船舶的加速度、速度成正比，是平台的重要水动力参数。在本节中，研究了该半潜式平台的纵荡、垂荡和横摇自由度的辐射阻尼与附加质量。

随着规则波频率增大，这些自由度的辐射阻尼表现出类似的变化规律。图8（a）显示，在横荡方向上呈现出两个峰值频率，分别为0.07 Hz 与0.14 Hz，且二阶峰值远大于一阶峰值。横荡辐射阻尼随着储油量的增加而增大，这是因为辐射阻尼是由结构的强迫运动引起的，它的大小与结构物截留的流体体积直接相关，流体的体积与垂直于强迫运动方向的横截面积成正比，满载时横荡方向的横截面积相比于空载多出210 m2。由图8（b）可知，垂荡辐射阻尼在计算频率区间内呈现出明显的二阶峰值，分别为0.08 Hz 与0.16 Hz。横摇辐射阻尼在0.12 Hz 处存在明显的峰值，如图8（c）所示。垂荡辐射阻尼与横摇辐射阻尼随储油量变化的规律与横荡辐射阻尼相反，且最大降幅分别约为22%与42%。这是因为在垂直方向上，截面积在储油量变化过程中未随吃水量的变化而减小，而是随着吃水量的增加而减小了等效质量系数。

图8 辐射阻尼Fig.8 Radiation damping

图9 附加质量Fig.9 Added mass

平台的横荡、垂荡与横摇附加质量有着相似的频域变化规律，在计算频率范围内均具有两个峰值。由于附加质量和辐射阻尼也是由结构的强迫运动引起的，因此附加质量在各自由度表现出的储油量变化特性均与辐射阻尼类似。图9（a）显示，横荡附加质量随储油量增多而增大，其增幅相较于横荡辐射阻尼更明显，最大增幅可达107kg。在图9（b）中可看出，垂荡附加质量在0.07 Hz附近随储油量增多而降低，然而在0.08 Hz 后随储油量增多而增加，这说明垂荡自由度的辐射效应的附加质量成分的变化规律受波浪频率影响较大。横摇附加质量随储油量变化的规律可分为三部分：在0～0.07 Hz区间内储油量越大，附加质量越高；0.07～0.11 Hz区间内，储油质量越大，附加质量越低；当波浪频率高于0.11 Hz 时变化趋势再次改变，且在0.13 Hz 附近满载横摇附加质量高出空载约108kg·m2/°，这个差值约为0～0.07 Hz区间内最大差值的5倍，如图9（c）所示。

3.4 幅值响应算子（RAOs）

幅值响应算子是直观反映半潜平台运动响应幅值的频域参量，其定义为波高1 m 的规则波浪激励下半潜平台的响应幅值。

图10（a）显示储油式半潜平台的横荡幅值响应算子随储油量变化不明显，在不同储油量下较为接近。图10（b）显示在0.035 Hz 处，横荡RAO 最大值与最小值相差约0.03 m/m，对应的储油量分别为3040 t 与15 800 t，因此半潜平台在横荡自由度上的响应大小不会随储油量的变化产生明显变化。由图11（a）可知，储油量越大，垂荡响应整体上越小，这是由于垂荡一阶波浪力随储油量的增加而减小，但半潜平台的质量随储油量的增加而增大。在峰值频率0.045 Hz 处，空载与满载垂荡RAOs 相差约1 m/m，这说明储油量的变化将更多影响平台在该频率附近的垂荡响应。图11（b）显示在0.04 Hz 处的垂荡幅值随储油量增加而增大，0.045 Hz处的幅值随储油量增加而降低，这说明垂荡幅值自然频率左移，其原因可能是平台质量的增大而导致。图12（a）显示横摇幅值响应算子整体随储油量的增加而增大，图12（b）则显示在自然频率两侧的两个计算频率处表现出相反的变化趋势，这说明横摇自然频率同样随储油量发生了偏移。在所有计算频率中，0.035 Hz 处的横摇幅值响应最大，在储油量6000 t 左右时该频率的横摇响应可达1.45°/m。

图10 横荡幅值响应算子Fig.10 RAOs of sway

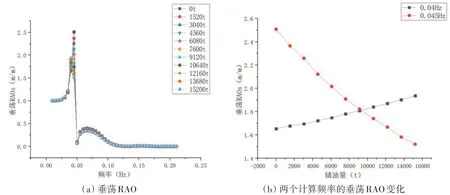
图11 垂荡幅值响应算子Fig.11 RAOs of heave

图12 横摇幅值响应算子Fig.12 RAO of roll

4 结 论

本文采用势流理论建立了新型立柱储油式半潜平台的水动力模型，并分析了在储油量变化时平台的频域特性，通过分析比对得到了如下主要结论：

（1）受吃水量变化的影响，半潜平台的横荡一阶波浪力随储油量的增加而增加，在0.07 Hz处最大增幅达1.6×106N/m。而横摇与垂荡一阶波浪力随储油量增加而减小，且前者降幅大，0.12 Hz 处的满载一阶波浪力相比于空载降低了5×107°/m。

（2）横荡辐射阻尼基本不随储油量发生改变，垂荡和横摇辐射阻尼与附加质量随储油量的增加有明显的减小，且最大降幅分别约为22%与42%，这说明横摇与垂荡自由度的辐射效应受平台储油量影响较大。由于附加质量与辐射阻尼均由结构强迫振动引起，附加质量随储油量变化规律类似于辐射阻尼，且横摇附加质量随储油量变化特性受波浪频率影响大，在计算频率范围内先随储油量增多而增大后表现出相反趋势，波浪频率大于0.11 Hz后受储油量影响明显，在0.13 Hz附近满载横摇附加质量高出空载约108kg·m2/°，这个幅值约为0～0.07 Hz区间内最大差值的5倍。

垂荡幅值响应算子整体上随储油量的增多而减小，最高空载垂荡RAO 比满载高出1 m/m，横摇幅值响应算子整体上随储油量的增多先增大后减小，在储油量为6000 t 左右时达到峰值1.45°/m，且两者均表现出明显的自然频率偏移，横荡幅值响应算子随储油量变化不明显。