输入受限无人帆船自适应航向跟踪控制
杨晓武,石 春,2
(1.贵州理工学院人工智能与电气工程学院,贵州 贵阳 550003;2.中交瑞通建筑工程有限公司,北京100176)
0 引言
舰艇、水下机器人和海上浮标常用于海上巡逻、资源勘测和海上环境监测,其需要携带大量的燃料,监测区域小,成本较高,相比之下无人帆船只需要携带较少的燃料,可以借助风力前行,同时帆船造价低,比较容易达到量产的目的。无人帆船通过自身传感器实时传输检测数据,与海上浮标相比较大扩大了监测范围。但海上环境复杂,大风、大浪等很容易作用于船帆以及船的龙骨,不仅会产生使帆船前进的力,还会出现横向的分力,导致帆船极难控制,产生横向漂移,从而使实际运行航线偏离预期航线[1]。当受到较大干扰时,为使帆船回到预期航线,则需要偏转较大的舵角,导致执行机构不能短时间接受较大值的偏转从而受到损坏。因此,在保持无人帆船的航向跟踪控制的前提下,执行机构得到最大的保护显得尤为重要,这成为许多科研人员的研究内容之一[1-5]。
目前,对航向保持控制,即固定航向跟踪和动态航向跟踪研究取得了许多成果。文献[4]最开始设计PID控制器调节航向,但需要基于具体模型才能整定参数。文献[5]接着通过递推最小二乘法对无人帆船运动响应模型进行在线辨识。文献[6]在原有的理论基础上结合刚体运动学建立了三自由度帆船运动数学模型。文献[7]在文献[6]的基础上将三自由度帆船运动数学模型变为关于控制舵角输入的仿射系统,同时利用RBF神经网络在线逼近无人帆船的未知模型。从文献[7]可知,改变帆船航向只需改变舵角,而舵角输入受物理约束。
执行器的输出有界约束是无人帆船控制问题的重要因素之一,影响控制系统的动态性能[8-9]。因此,在设计鲁棒自适应跟踪控制器时,要加以考虑。同时,在许多实际控制系统中,未知控制系数也是影响控制器设计的客观因素,不能利用传统的控制设计方法获取控制器,而Nussbaum自适应控制技术可以抑制具有未知控制系数的无人帆船控制引入的问题[10-16]。文献[16]针对一类具有未知控制系数的不确定非线性系统,提出了一种自适应神经网络控制方法。文献[17]利用分段Nussbaum函数解决了多未知控制方向问题。考虑到帆船海上航向极易受到干扰,为使受到干扰时能够快速使系统保持稳定,文献[10]利用RBF神经网络结合滑模控制对干扰项进行补偿,同时能够使系统快速稳定,提高系统的鲁棒性。
基于上述讨论,本文针对具有输入受限且存在未知控制系数情形的无人帆船航向控制问题,提出了一种满足存在未知模型且存在风、浪等外界干扰的3自由度帆船航向跟踪控制方法[18]。
1 帆船数学模型
帆船分成船帆、船舵、龙骨和船体4部分,结合气体流体动力学理论和机翼理论对各部分进行受力分析,忽略帆船的起伏运动和纵摇运动建立3自由度帆船运动数学模型。本文考虑外界干扰和实际控制输入舵角的有界性帆船模型为
(1)
ψ∈RM和r∈RM分别为系统状态变量;u∈RM为前进速度;v∈RM为横移速度;δs∈RM为帆角;δr∈RM为舵角。f2=f1+d,f1为帆船未知模型的非线性函数,d为外界干扰,考虑到大自然能量有限则干扰未知但有界d≤dN;gr为未知控制增益其符号未知;δr为系统的输出;u(δr)为受执行器饱和约束特性的输出控制量,且饱和受限函数为
(2)
sat(δr) 为关于δr的饱和函数;sgn(δr) 为关于δr的符号函数;uM为控制器输出控制量的最大值。
2 输入受限自适应控制器设计
为方便设计鲁棒跟踪控制器,引入Nussbaum增益技术解决控制系数未知的问题,可以不断地切换符号和增加幅值,导致系统状态不断发生切换,使得系统状态可以不断趋向设计的平滑面,最终使状态趋于稳定,达到控制要求。因此,Nussbaum增益函数可以有效解决控制系数未知的问题。Nussbaum函数的具体定义及相关引理如下:
定义1:如果函数N(χ)满足下面条件,则N(χ)为Nussbaum 函数。Nussbaum函数满足如下双边特性,即
(3)
根据Nussbaum函数定义,Nussbaum函数为
N(ξ)=ξ2cosξ;N(ξ)=ξ2sinξ
(4)
ξ为Nussbaum函数的变量。
引理1:如果V(t)和ξ()为定义在[0,tf)的光滑函数,存在V(t) ≥ 0,∀t∈[0,tf),且N()为光滑的函数,gr为时变增益函数,如满足式(5),则函数V(t)、ξ(t)以及在∀t∈[0,tf)必定有界。
(5)
n为1个合适的常数。
引理2:(Barbalat引理)如果f(t)是连续可导函数且当t→∞时,其极限值存在,若其导数一致连续有界,即当t→∞时,f(t)的导数趋近于0。
鲁棒跟踪控制器设计过程如下:
航向误差h为
h=ψ-ψd
(6)
ψ∈RM为实际航向;ψd∈RM为期望航向。为减小输入受限对整个帆船系统造成的影响,引入2个新的辅助状态变量λ1、λ2,当系统控制达到饱和时可帮助控制输入退出饱和,设计误差辅助系统为
(7)
Δδr=sat(δr)-δr。同时为保证当t趋于无穷时λi趋于0则需要c1> 0、c2> 0;同时为防止δr过大时造成辅助系统不稳定,则需要选择更大的c1和c2。则可解释为当系统出现饱和时,该辅助系统内部将会立即起作用,帮助系统退出饱和。当系统不饱和时Δδr= 0,λ1、λ2将会呈指数衰减。
重新定义航向误差为
e1=e=ψ-ψd-λ1
(8)
对式(8)求导得
(9)
根据式(1)、式(8)和式(9),闭环误差系统可描述为
(10)

定义滑模函数为
(11)
其中,c> 0。
对式(11)求导得
(12)
其中,f(λ1,λ2) =c1( -c1λ1+λ2) +c2λ2。f2通过RBF神经网络进行在线逼近为
(13)

f(λ1,λ2)+ηsgn(s)+σs]
(14)
N(ξ)为Nussbaum 函数,即
N(ξ)=ξ2cosξ
(15)
为抑制系统不确定性对闭环误差系统的影响,RBF神经网络权值自适应律设计为

(16)
其中,γ> 0。
Nussbaum函数中变量ξ的自适应律为
f(λ1,λ2)+ηsgn(s)+σs]
(17)
当系统存在未知模型时,采用RBF神经网络进行在线逼近,由于其理想权值无法测量采用自适应控制方法并设计相关的权值自适应律,在控制工程中,常常存在控制系数未知的约束问题,引入Nussbaum自适应增益技术,能够有效解决该问题,考虑到帆船控制的舵角只能在有限范围,引入输入受限函数,设计辅助系统当系统出现饱和时,能够及时退出。利用滑模控制,可以抑制神经网络产生的逼近误差,同时能够增加系统的鲁棒性。
3 控制算法稳定性分析
为使整个闭环系统的信号有界,保证航向控制趋于预期航向,达到控制目的。本节用下面定理给出主要结果:
定理1:针对无人帆船模型系统,在不确定模型、控制系数、外界干扰未知及控制输入受限共存的情况下,借助辅助系统、神经网络权值自适应律、变量ξ自适应律,在控制器的作用下,设计参数c、η、σ、γ、λ1和λ2,可保证无人帆船航向误差闭环控制系统所有信号的一致最终有界性。
证明:根据以上内容构建李雅普诺夫能量函数为
(18)
则重新变换式(8)得
(19)
对式(18)关于时间进行求导,可得
σs2-η|s|+sε
(20)
将式(17)和式(13)代入式(20),令η≥εN+dN,则式(20)可改写为
(21)
对式(21)两边进行积分,可得
(22)
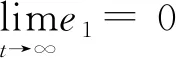
为获取平滑的控制输入,在系统仿真验证阶段,可利用双曲正切函数来替换趋近律中符号函数。
4 仿真结果分析
为验证该理论同时验证设计的控制器的有效性,进行MATLAB仿真实验,为便于分析说明而不失一般性,设无人帆船的预期航向ψd=sint。选择参数c= 10、σ= 1、γ= 1、η= 0.1、λ1= 10、λ2= 10。选取x= [ψ,r]T为神经网络的输入,被控对象初值为[0.2,0],根据网络输入ψ和r的实际范围来设计高斯基函数的参数:参数ci在[1.5,1.5]平均分布,参数bi为3.0。神经网络权值的初始值分别取0.1、0.2、0.1、0.2、0.1。仿真结果如图1~图7所示。

图1 航向角跟踪
图1和图2分别是航向角和航向角速度跟踪演变曲线,跟踪效果满足控制精度要求,响应速度快,在较短的时间内达到稳定。图3是引入Nussbaum函数N(ξ)及其参数ξ后,随着时间的不断变化,N(ξ)及其参数ξ能够趋于稳定,表明使用该方法可以解决控制系数未知问题,控制输入加入辅助系统之后有助于解决无人帆船执行器有界输入约束问题。图4是利用RBF神经网络逼近未知模型。图5和图6分别表示改变切换函数控制器输出对比和改变切换函数受限控制器输出对比,通过仿真表明将趋近律中符号函数替换成双曲正切函数,明显削弱了闭环误差系统输入抖振,同时控制系统状态不会发生激烈改变,使控制器不会在短时间内正负幅值反复切换,保证执行器的平滑输出,节约能量,通过对比发现受限控制器能够限制控制输出,使控制器能够在一定范围输出,满足实际工程中执行器设计需求。图7为输入受限前后差值δr,表明当系统未稳定时,系统过早的出现过饱和状态。本文设计辅助系统帮助控制器在极短时间内退出饱和,防止控制器运行失控,保证无人帆船稳定运行。

图2 航向角速度跟踪

图3 Nussbaum函数N(ξ)及其参数ξ
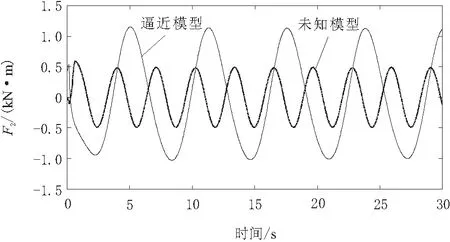
图4 神经网络逼近未知模型

图5 改变切换函数控制器输出对比

图6 改变切换函数受限控制器输出对比

图7 输入受限前后差值δr
5 结束语
本文研究了具有未知控制系数的无人帆船在海上航向持续跟踪控制问题。针对实际控制工程中存在执行器输入受限,帆船的部分模型未知以及外界干扰共存情形,提出一种鲁棒自适应控制算法,该算法引入Nussbaum函数来解决未知控制系数问题,利用RBF神经网络技术拟合未知控制模型。根据滑模控制理论,设计了误差退出饱和辅助系统,给出基于Nussbaum技术的自适应律,设计指数趋近律,为获取平滑控制输入,将趋近律中的符号函数替换为双曲正切饱和函数,所提算法能使系统快速响应,达到稳定,同时削弱了系统抖振。仿真结果表明,控制系统在设计控制算法的左右下能快速稳定,跟踪效果好,验证了设计的控制器的有效性。

