无限脉冲响应切比雪夫数字带通滤波器的设计
何颖,安晓莉
(西安思源学院 电子信息工程学院,陕西西安, 710038)
0 引言
数字信号的处理在最近的几年中发展迅速,是最有前景的学科之一。数字信号处理是指的将连续的模拟信号经过采样和模数转化,成为数字信号,输入到计算机中进行处理,在数字信号处理的内容中,信号滤波是最重要的一个环节。对信号进行滤波是现在的各种电子信息产品所必备的,滤除掉不要的或者说干扰的频率信号留下需要的频率信号[1~2]。
对数字信号进行滤波引起了国内外专家学者的广泛关注,数字滤波器的设计工作在世界范围内的研究如火如荼地进行中。由于数字信号滤波器具有众多的优点,如:可靠性高、准确性高、灵活性高等,从而被广泛地应用于各行各业。随着信息时代的进一步发展,数字信号滤波的需求和要求也是不断提高,数字滤波器的分析和设计变得更为重要[3~5]。
利用MATLAB进行数字滤波器的设计和分析可以更为方便地为实际的滤波器的设计提供思路和想法。能够极大地缩短滤波器研发和设计所用的时间,并能够获得更高的设计性能。
无限长脉冲响应(IIR)数字带通滤波器设计时,首先给定数字滤波器的性能指标,然后按照频带变换转换成相应的模拟滤波器的性能指标,进行模拟滤波器的响应设计,最后根据双线性变换原则将模拟滤波器变换成数字滤波器。
1 傅里叶变换
傅里叶变换是建立以时间为自变量的“信号”与以频率为自变量的“频谱函数”之间的某种变换关系。性能指标变换规则有冲激响应不变法、阶跃响应不变法、双线性变换法等。双线性变换法可以较准确地控制截止频率的位置,克服了产生频率响应的混叠失真,稳定的模拟滤波器经双线性变换后所得的数字滤波器必定稳定,双线性变换法为了克服多值映射,首先把整个s平面压缩变换到某一中介的s1平面的一条横带中,变换关系为即得再通过变换z=es1T把横带映射到z平面上,实现了s平面与z平面的一一对应关系。
2 切比雪夫低通滤波器
切比雪夫滤波器是一种在通带中等波纹、阻带中单调的滤波器,称为切比雪夫Ⅰ型[6~8]。其低通滤波器幅度响应为:
式中,ε为小于1的正数,表示通带波纹大小的一个参数,ε越大,波纹也越大。N代表滤波器的阶次,
3 离散周期序列的傅里叶级数(DFS)
给定信号为:
x(t) = 30sin(2π⋅10 ⋅t) + 30sin(2π⋅ 2000 ⋅t) + 30sin(2π⋅ 6000 ⋅t)
(1)求x(t)的傅里叶变换:
可先将x(t)其展成指数型,对比FS反变换公式:x(t)=求出傅里叶级数的系数X(jkΩ0)。对x(t)采样得x(n),求:
因篇幅有限,7200个点图像过于密集,图1只给出X~(k)在k=−6 50,… , 0,… , 650区间的频率特性。可看出,图形关于原点共轭偶对称,即幅频特性为偶函数,相频特性为奇函数。事实上,在k= 0,1,… , 7199周期里,有
可得X~(k)的频率特性如图1所示。k= 1,200,600,6600,7000,7199幅值为108000,并且相频特性关于(3599.5,0)对称。
2)将电熔套管从包装袋中取出,并检查确认配件内壁是干净的。如有需要,可使用酒精擦拭纸擦拭电熔套管内壁,在开始焊接工艺前,确保清洁后的电熔套管内壁是完全干燥。
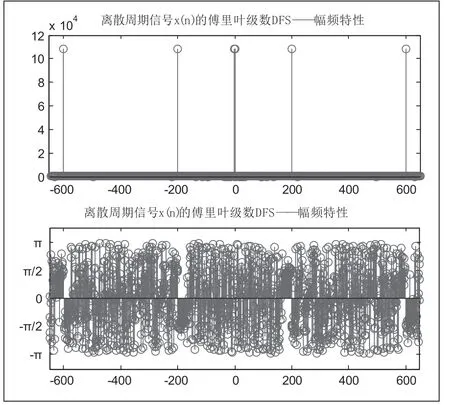
图1 的频率特性
4 切比雪夫滤波器运算设计
■4.1 模拟带通滤波器
①求ε和N。
取N为最小正整数N=2。
②求3dB截止频率Ω3dB。
把N=2代入到阻带指标要求公式中,阻带指标满足要求,且由于N= 2 > 1.7747,因而通带指标一定超过要求。将N=2代入阻带条件,可得:
归一化参数:
③查表法求解切比雪夫低通滤波器G(p)。
根据N=2,查表可得归一化原型滤波器,
④模拟低通到模拟带通的转换。
根据题目要求,分母整理为常1多项式,即分子分母同时除以 2.4812×1016,可得H(s)。
■4.2 数字带通滤波器
根据题目要求,分母整理为常1多项式,即分子分母同时除以20
4.3983×10 ,可得:
将系统函数系数代入表1,即可得到IIR带通滤波器的直接Ⅱ型结构。
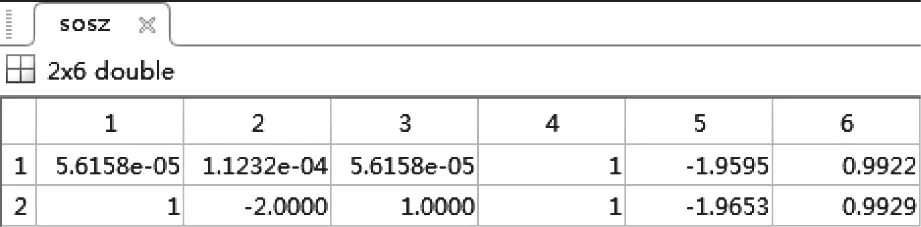
表1 IIR带通滤波器的直接Ⅱ型结构
5 实验及结果分析
■5.1 模拟滤波器分析
图2、图3,分别从时域和频域对切比雪夫模拟带通滤波器进行分析,滤波器满足题目要求的各项性能指标,且具有良好的稳定性、快速性和准确性。
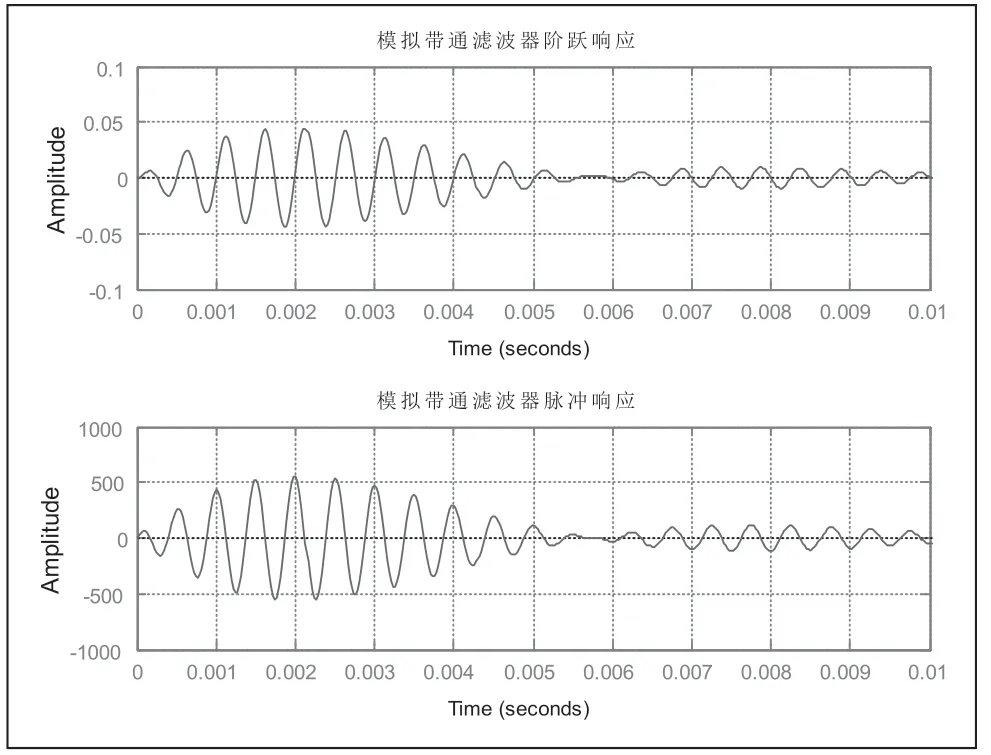
图2 切比雪夫模拟带通滤波器阶跃响应和脉冲响应
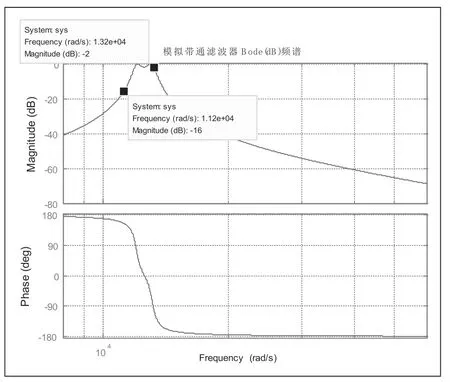
图3 切比雪夫模拟带通滤波器频谱图
从图3中,幅频图中可以明显看到切比雪夫滤波器最大的特点:波纹特性,从相频图中可以看到其最大的优点,相比巴特沃斯滤波器,频率响应曲线之间的误差最小。由于该波纹的谷值接近要求的通带衰减,导致该参数下切比雪夫滤波器幅值失真。如图4、图5,将切比雪夫模拟带通滤波器的输入和输出进行对比,发现输出函数的幅值不是2000Hz分量的幅值30,而仅为24。图5中给出当输出波形尚未稳定时与输入信号2000Hz分量几乎重合,这意味着在该暂态过程中滤波器滤去了低频和高频谐波。而稳态后,相位没有偏差,仅在幅值上存在一定差值。可以通过校正,以增益系数来改变切比雪夫滤波器。
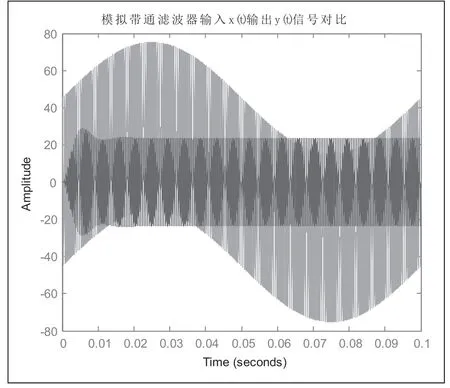
图4 切比雪夫模拟带通滤波器输入输出信号对比
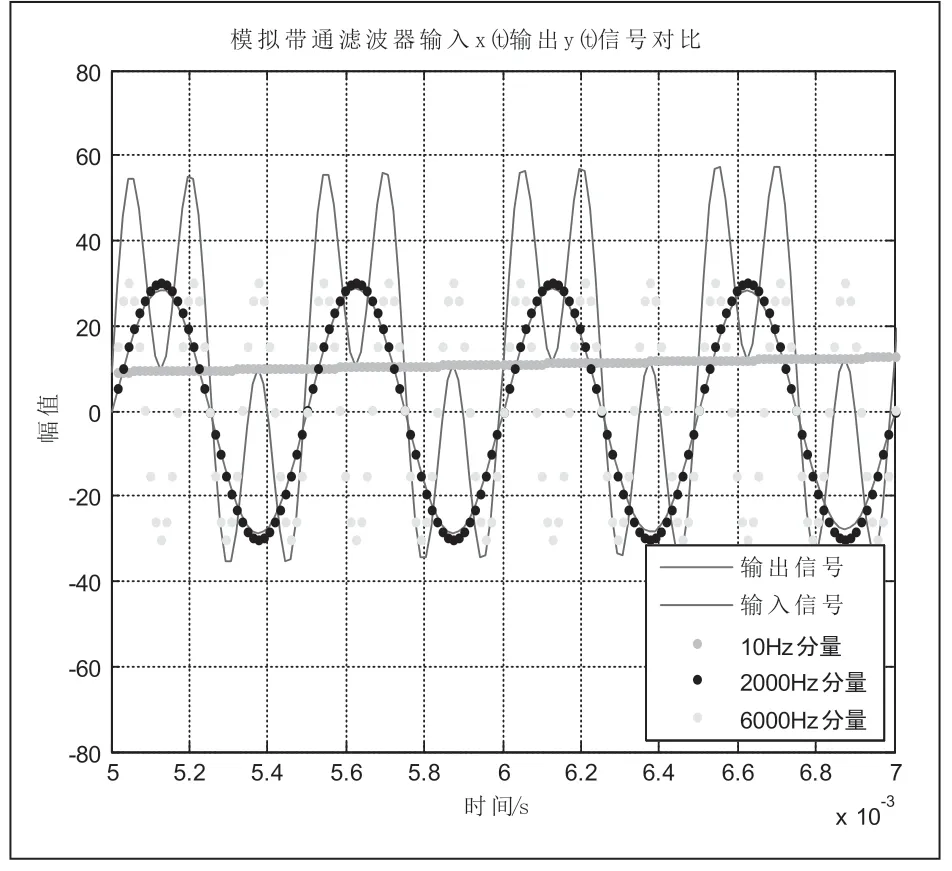
图5 切比雪夫模拟带通滤波器输入及各分量与输出信号的对比
■5.2 数字滤波器分析
图6、图7分别从时域和频域对切比雪夫数字带通滤波器进行分析,滤波器满足题目要求的各项性能指标。图6中,其稳定性、快速性和准确性看起来相对巴特沃斯波动次数较多。
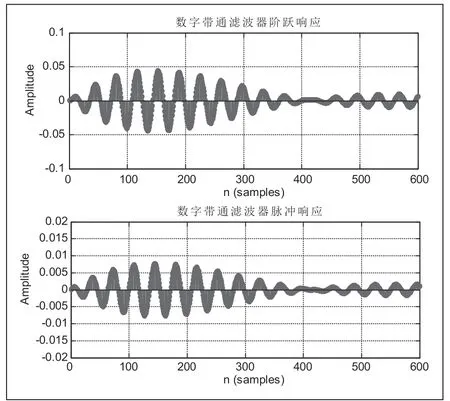
图6 切比雪夫数字带通滤波器阶跃响应和脉冲响应
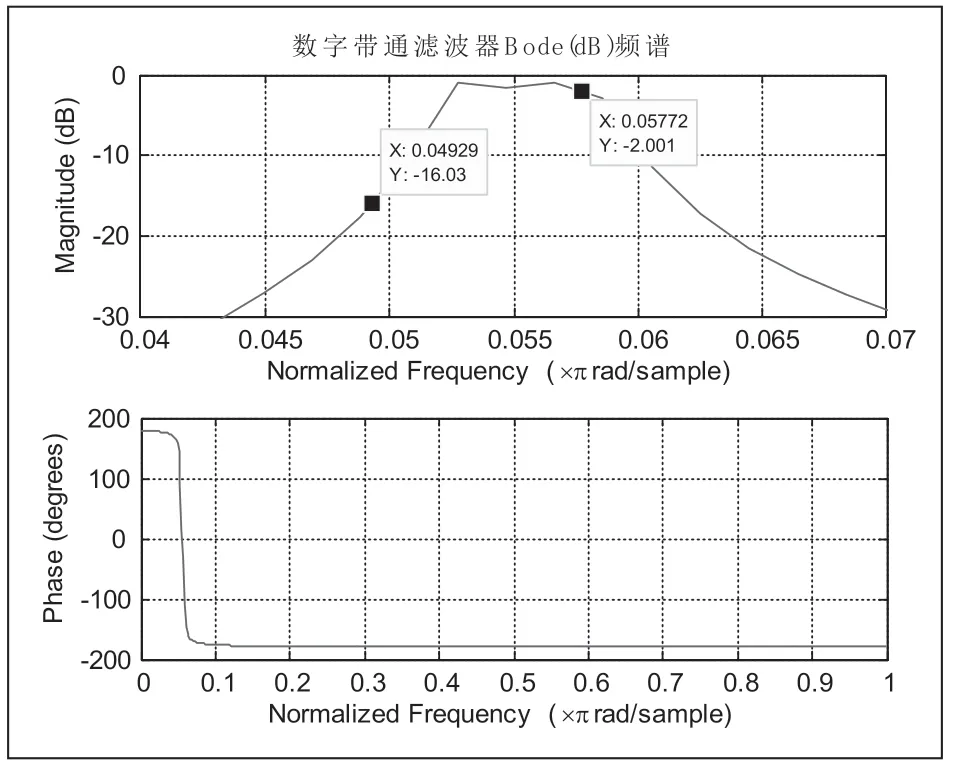
图7 切比雪夫数字带通滤波器的频谱图
图8将切比雪夫数字带通滤波器的输入和输出进行对比。相比最平的巴特沃斯滤波器,存在一定的幅度失真。
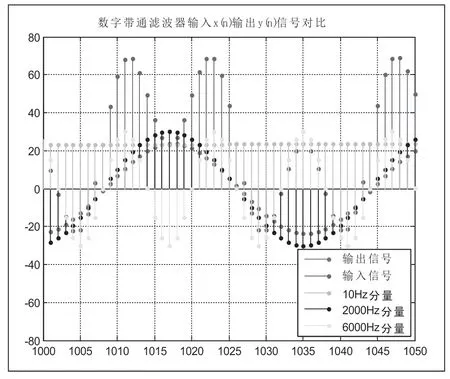
图8 切比雪夫数字带通滤波器输入及各分量与输出信号的对比
图9给出了切比雪夫数字带通滤波器输出信号的频谱图,可见图1所示抽样信号经过滤波器之后,只剩下2000Hz频率,满足题目要求。说明切比雪夫带通滤波器之后,相位没有发生失真,仅仅有幅值不满足要求,故采用增益校正可行。
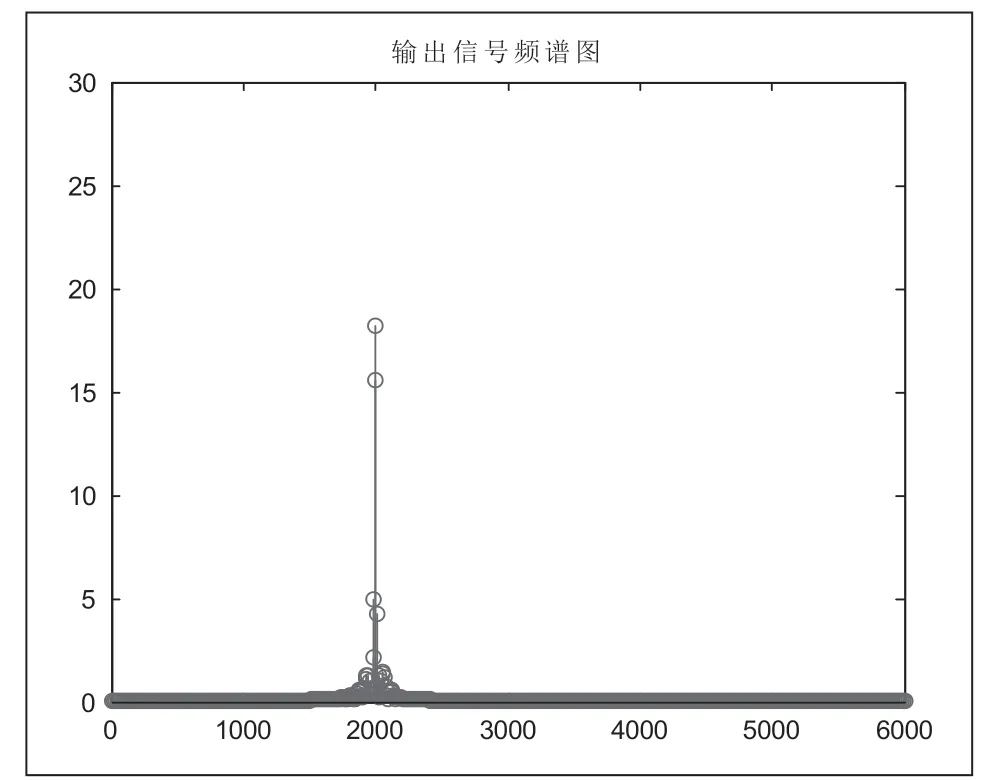
图9 切比雪夫数字带通滤波器输出信号频谱图
6 结论
切比雪夫滤波器在过渡带比巴特沃斯滤波器的衰减快,其经济性会更好,但频率响应的幅频特性不如后者平坦。切比雪夫滤波器和理想滤波器的频率响应曲线之间的误差最小。就其输出效果而言,在相同指标下,切比雪夫滤波器的阶次较小,但对于带通滤波器而言,由于切比雪夫Ⅰ型滤波器在通频带内存在幅度波动。

