基于GA-BP神经网络的股票收盘价预测

摘  要：為提高BP神经网络预测股票收盘价的准确性和高效性，文章使用Python语言，通过遗传算法（GA）对BP神经网络算法中的权值和阈值进行优化（GA-BP），并将优化后的系统用于股票预测当中。优化后的算法收敛速度更快，同时克服了BP算法容易陷入局部最优的缺陷，提高了整个系统的预测精度。最后对股票“千金药业”的仿真结果表明，该方法在股票收盘价的短期预测方面具有一定的应用价值。此外，在对股票收盘价预测过程中，添加输入参数盘口，能够有效降低GA-BP神经网络的预测误差。

关键词：遗传算法优化；BP神经网络；股票预测

中图分类号：TP391.4  文献标识码：A  文章编号：2096-4706（2023）20-0147-04

Prediction of Stock Closing Price Based on GA-BP Neural Network

CHEN Shuai

（Xinhua College of Ningxia University， Yinchuan  750021， China）

Abstract： In order to improve the accuracy and efficiency of BP neural network in predicting the closing price of stocks， this paper uses Python language to optimize the weights and thresholds of BP neural network （GA-BP） through Genetic Algorithm （GA）， ， and uses the optimized system in stock prediction. Compared with BP， the optimized algorithm converges faster and overcomes the defect of BP which is prone to fall into local optimization， improving the prediction accuracy of the entire system. Finally， the simulation results of the stock named “Qianjin Medicine” show that this method has certain application value in short-term prediction of stock closing prices. In addition， in the process of predicting the closing price of stocks， adding input parameters named “Pan Kou” can effectively reduce the prediction error of the GA-BP neural network.

Keywords： Genetic Algorithm optimization; BP neural network; stock prediction

0  引  言

随着市场经济的发展，证券市场作为二级市场的主要组成部分，越来越受到投资者的青睐，投资者希望准确地预测股票价格，从而把握股票走向，使收益最大化。股票价格的变化具有非线性，传统的SVM、决策树、线性回归模型对于股票的预测虽然有较好的表现，但应用广泛的BP神经网在股票预测中表现一般。主要是BP神经网络存在如下缺陷：收敛速度慢；容易陷入局部最优，从而无法得到全局最优解[1，2]；网络结构难以确定[3]。而遗传算法（GA）具有良好的并行性以及全局最优性，既能够降低BP神经网络陷入局部最优解的风险，又能够优化的初始权重和阈值，从而提高了BP神经网络的稳定性。

本文采用遗传算法优化BP神经网络进行股票市场的短期收盘价预测，充分利用BP神经网络的学习能力和GA算法的全局搜索能力。

1  BP神经网络和遗传算法

1.1  BP神经网络算法

标准的BP神经网络由输入层、隐含层、输出层这三部分组成，其中输入输出层为单层结构，隐藏层为单层或者多层结构，层与层之间各节点完全连通，隐含层中每层各节点相互不连通[4]。拥有一个隐藏层的BP神经网络模型如图1所示。

整个BP神经网络可以看成是一个n维向量x = （x1， x2， x3，…，xn）T到一个m维向量y = （ y1， y2， y3，…， yn）T的映射，获取预测结果后，根据误差通过反向传播对权值和阈值进行调整，如此反复循环直到误差足够小或循环次数达到最大值时结束模型训练。如图1所示，wij为链接神经元i和神经元j的权值，θ为阈值。则单个神经元j的输出与输入的关系表示为：

激励公式选用sigmoid函数，经过激励函数得到该层正向传播的最终值yi，公式如下：

yi为系统输出值，Yi为真实值，e为输出值与真实值的均方差，公式如下：

根据每次迭代的误差值，按梯度下降的方向，更新各个节点的权值，更新权值公式如下，其中φ为更新速率也就是后文中所说的训练速率。

1.2  遗传算法

遗传算法借鉴了达尔文的进化论和孟德尔的遗传学说，通过计算机模拟自然进化过程，从而实现全局搜索，该方法具有高效性、并行性、全局性的特点[5]。GA算法主要步骤有：染色体编码、初始化种群、适应度函数评估、择优选择、基因交叉、基因变异和产生后代[2]。在GA算法中，每一条染色体对应GA算法的一个解决方案，初始化种群就是生成包含多种解决法案的个体，这些初始的个体基因组合应该包含问题的最优解。通过适应度函数来衡量方案的优劣，选择优良的个体基因，以繁衍后代。而繁衍的过程就是“基因”进行交换和突变的过程，通过突变可以增加种群基因的多样性，避免整个种群陷入局部最优。最后将进化后的最优个体的“基因序列”进行解码，得到最终解。本文将GA与BP神经网络相结合，用于股票收盘价的预测，从而克服了BP算法收敛速度慢、容易陷入局部最优等不足。

2  基于GA算法優化的BP神经网络

本文使用Python语言，通过遗传算法，对BP神经网络中的权值和阈值进行优化。在BP神经网络中，当确定权值和阈值时，整个BP网络模型也随即确定，但在单独使用BP网络反向传播时，发现整个模型容易陷入局部最优，所以本文将BP网络中所有的权值和阈值编码成GA算法中一个个体基因序列[w11， …， wij， θ1， …， θj， w11， …， wj1]，通过GA算法fitness适应度函数来寻找最优权值和阈值序列。适应度函数返回值为BP网络中输出值与真实值的欧几里得距离。

具体流程如图2所示，首先需要设定BP神经网络的隐藏层个数以及各隐藏层的神经元个数，通过实验调整初始BP神经网络的结构。然后将样本输入到BP神经网络中进行迭代，迭代一定轮数后，将BP神经网络中的阈值和权值转换成遗传算法中个体的“基因序列”，该过程称为染色体编码，编码过程需按照每层神经元节点的权值和阈值依次排列，并将排列好的序列转化成二进制序列作为初始种群中个体的“基因序列”。然后初始化种群，构建初始种群时将不同的训练数据依次进行BP迭代，以获取不同的权值、阈值序列作为初始种群的“基因库”，生成多个个体，一般初始种群个体数量不少于20。计算初始种群的适应度，根据fitness适应函数筛选优秀个体，筛选后的优秀个体通过交叉和变异产生后代，以下为GA交叉算法的Python代码实现：

后代个体“基因编码”具有BP神经网络全部的权值和阈值，再将筛选后的优秀个体的基因解码后，得到BP的权值和阈值。系统再通过BP神经网络得到预测结果，根据预测结果和实际结果的误差值构建适应度函数，淘汰适应度差的个体并筛选出种群中的优秀个体。优秀个体保留，并通过“基因序列”的交换和突变产生新的个体，再根据适应度函数进行筛选，如此循环，直到种群中出现满足误差小于设定误差值的优秀个体或者种群代数达到临界值时结束循环。最后，再将种群中最优个体的“基因”解码成BP神经网络中的权值和阈值，以构建最终模型。

3  股票收盘价预测仿真

3.1  数据获取

运用Python第三方库Tushare获取“千金药业”（证券代码：600479）2022年1月1日到2022年12月31日的历史行情数据，共获得300组数据并将此数据集分成训练集和测试集两部分，预测未来10个交易日的收盘价。其中训练集240组，测试集60组数，每组数据由若干输入参数和10个交易日后的收盘价构成。然后将240组数据再分为20小组，每小组有12组数据，这12组数据用来确定BP神经网络中的一组权值和阈值，将确定的权值和阈值编码，生成GA初始种群中的一个单独个体，这样一共得到20个个体作为初始种群。

3.2  GA-BP输入参数的选择

股票市场中每时每刻都产生大量数据，本文数据输入参数包括：每日开盘价、收盘价、最高价、最低价、成交量以及盘口。并对原始数据进行归一化处理，以减少数值范围波动对系统的影响。其中盘口选自东方财富网站中投票统计值，该值是统计看涨人数的占比情况，该项数据更能体现人们对股票走势的期望。再结合上文提到的5种输入参数，就能够准确地反映出股票的波动特征。输入参数分为两组，第一组输入参数只有开盘价、收盘价、最高价、最低价、成交量5个输入参数，第二组输入加入盘口参数也就是有6个输入参数。两组参数用于对比盘口参数对预测结果的影响。

3.3  GA-BP基础参数设定

BP网络层数：3层网络结构，即输入层、隐藏层、输出层。

BP隐藏层节点个数：经过实验得到隐藏层节点个数为8个时较为合适。该参数的设置对模型预测的精度有很大的影响，隐藏层节点数量和隐藏层层数过多，会导致训练率底下，增加模型迭代的时间开销，降低训练效率；而过多的训练又容易导致过度训练从而出现过拟合现象，使得预测精度降低。本文通过如下公式获取隐藏层节点个数： 其中N为隐藏层节点个数，n为输入层节点个数，m为输出层节点个数，a为1到10之间的常数。

BP神经网络权值初始化：随机产生一组-0.5到+0.5的随机数作为权值的初始值。训练速率设置为0.5。BP网络最大迭代次数设置为12轮，用于生成遗传算法中的初始种群。最小误差取值为0.000 1，当两轮迭代误差值小于最小误差时，可提前结束迭代。激励函数使用Sigmoid函数。种群初始化采用BP进行12轮迭代后的阈值和权值作为最初种群的一个个体基因。种群规模为20。变异概率取值为0.05，变异概率过小，种群的多样性下降太快，容易导致有效基因的迅速丢失且不容易修补；而变异概率过大，尽管可以保证种群的多样性，但很大程度上会破坏已存在的有利模式，导致难以收敛。交配概率选取0.6，交配概率过大容易破坏已有的有利模式，随机性增大，容易错失最优个体；而交配概率过小则不能有效地更新种群。遗传算法中交叉策略选取两点交叉法。进化代数选取100为最大进化代数。

3.4  仿真结果分析

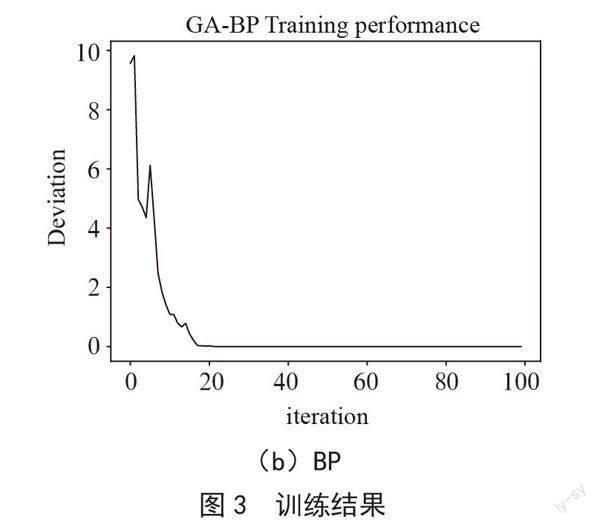
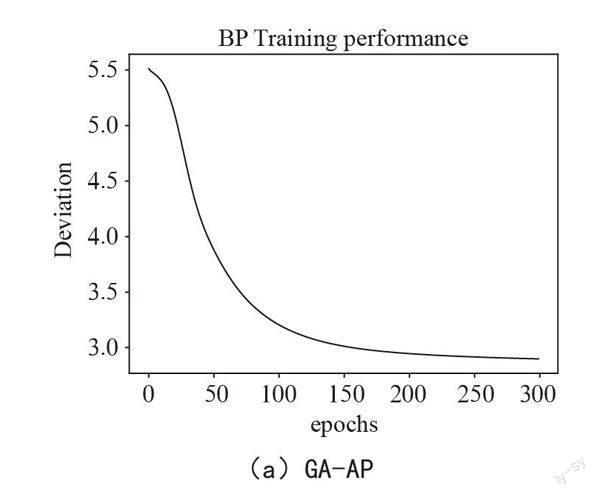
从图3可以看出，训练过程中GA-BP的收敛速度较快，误差值随着迭代次数的增加逐渐减少，只需大约18轮迭代，就基本收敛，模型趋于稳定；而传统的BP神经网络，收敛速度较慢，需要将近300次迭代才能收敛。从训练集的收敛速度上来看，优化后的GA-BP效率更高。此外GA-BP迭代初期出现较大范围波动，反映出GA算法模拟种群进化过程中的不确定性，而BP的反向传播梯度下降法使得系统的整体误差随着训练次数的增多，平滑下降。此外对于GA-BP而言，由于收敛速度较快，迭代次数不易过多，以避免出现过拟合现象。从图中还能观察到GA-BP系统的进化代数在15到20代时较优，在20代以后容易出现过拟合现象。

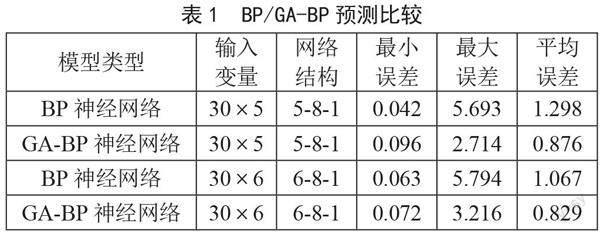
训练数据放入GA-BP中进行训练后，再对60组测试数据进行预测，预测误差如表1所示。

根据表1数据可以得到，相对于BP神经网络，改进后的GA-BP神经网络平均误差值更小。GA-BP神经网络利用遗传算法的全局搜索能力，有效地克服了标准BP神经网络局部收敛的弊端，预测结果更加精准。此外输入参数的选取也对预测结果的精度产生一定的影响，当输入参数加入盘口参数后，系统的最小误差更小，最大误差更大，而整体预测精度有所提高。

4  结  论

GA-BP神经网络模型克服了标准BP神经网络容易陷入局部最优，收敛速度慢的弊端，使得该模型可以有效地提高对股票收盘价格短期预测的精度。输入参数盘口的引入，能够降低GA-BP神经网络预测的误差，提高预测精度。该方法在股票预测方面有较高的应用价值。

参考文献：

[1] 富宇，李倩，刘澎.改进的BP神经网络算法的研究与应用 [J].计算机与数字工程，2019，47（5）：1037-1041.

[2] 墨蒙，赵龙章，龚嫒雯，等.基于遗传算法优化的BP神经网络研究应用 [J].现代电子技术，2018，41（9）：41-44.

[3] 魏海坤.神经网络结构设计的理论与方法 [M].北京：国防工业出版社，2005：234.

[4] DING S，ZHANG Y，CHEN J，et al. Research on using genetic algorithms to optimize Elman neural networks [J].Neural computing and applications，2013（23）： 293-297.

[5] 杨梅，卿晓霞，王波.基于改进遗传算法的神经网络优化方法 [J].计算机仿真，2009，26（5）：198-201.

作者简介：陈帅（1989—），男，汉族，宁夏银川人，助教，硕士，研究方向：多媒体与感知。

收稿日期：2023-03-26