改进粒子群算法在电力调度自动化中的应用研究

龚 舒,江雄烽,刘 雯,谢 虎

(1.广西电网电力调度控制中心，广西 南宁 530000; 2.南方电网数字电网研究院有限公司，广东 广州 510000)

0 引言

第二次工业革命后，电力企业变得非常重要。电力企业系统出现不可控制的故障时，会对国家会造成严重损失。神经网络模型凭借其强大的非线性处理能力在电力自动化设备评估中被广泛使用，为设备提供了较为准确的评估结果[1]。现阶段，神经网络训练的方法大多为后向传播算法[2]。因为后向传播算法用的是梯度下降的原理，导致模型存在无法匹配最优解以及收敛速度慢的问题。智能电网的大环境趋势下，国家对电力调度自动化设备状态评估提出了新的要求。针对电力调度自动化设备状态评估模型的优化，改进的粒子群算法已成为解决问题的突破口。

群体智能算法是以种群为基础的相关算法。粒子群算法在相关类型中使用较多[3]。现阶段，很多国家的学者把粒子群优化算法的改进总结为以下几个方面。①粒子群优化算法的参数不多，但是参数的值却对算法的性能有很大影响[4]。在参数寻优的方式上，粒子群优化算法通过调整拓扑结构、子种群与其他智能算法的协作策略来优化粒子寻优方式。②大规模多目标优化的明显弊端是维度较高。如果维度突破一个数量级，则无论用什么方法去调整参数或运用优秀的寻优策略都将于事无补。因此，把目标定位在怎样优化粒子群算法的维度，对于提高算法性能至关重要。③粒子群算法的解空间可以分割成多个子空间。每个子空间给予维度改良，从而对整个种群进行降维优化，使收敛速度也有所增强。不足的是，因为大量的特征维度让问题变得复杂，以往的粒子群算法和其他相关算法的机制使得算法不能拓展搜索空间。当算法陷入局部最优后，跳出高维度的局部最优就会很难，并会导致收敛过早且收敛精度不够。

本文在正态分布衰减惯性权重的基础上提出自适应变异优化策略，给出一种基于正态分布衰减惯性权重的粒子群优化(normal distribution decay inertial weight particle swarm optimization，NDPSO)算法。NDPSO算法的惯性权重在前期保持较大的取值，使得粒子群算法在寻优时保持较大的步长[5]；后期惯性权重保持较小的取值，兼顾了全局搜索和局部开发的能力。通过算法仿真和结果分析，本文证明正态分布衰减惯性权重策略能够从参数改进角度平衡全局搜索和局部开发能力，在保证收敛精度的同时加快了收敛速度。改进的粒子群算法可以提高神经网络模型处理复杂问题的能力，从设备状况信息中获取设备的状况特征，为找到最优解奠定基础。这将为电力调度自动化设备进行更快、更精准的评估提供可能，并为管理人员提供技术支撑。

1 研究方法

1.1 群体智能优化算法

群体智能指的是现实中的个体利用共享信息完成相互之间的合作，从而都拥有辨别问题的能力[6]。

蚁群优化算法是基于概率技术的元启发式算法，一般用于复杂优化问题寻优[7]。蚁群优化算法的原理是：蚂蚁无目标游走，在经过食物周边时留下相关信息[8]，说明此处存在食物；其他蚂蚁看到标记后，有可能在这条路进行游走[9]。人工蜂群算法是以自然界中蜜蜂觅食为原理的优化算法[10-12]。粒子群优化算法是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。 通常认为粒子群优化算法是群集智能的一种。三种算法各有优缺点：蚁群算法优点是鲁棒性好，缺点是收敛性能较差；人工蜂群算法优点是局部搜索能力较好，缺点是很容易陷入局部最优解；粒子群优化算法优点是算法简单、搜索能力快，缺点是优化精度易受干扰。

1.2 改进参数设置的粒子群优化算法

线性衰减惯性权重粒子群优化算法推出后，其速度计算式也发生改变，表达为：

(1)

(2)

式中:ωmax、ωmin分别为规定的最大惯性权重与最小惯性权重;T为最大迭代次数。

本文取ωmax=0.9、ωmin=0.4，则位移式为：

(3)

线性衰减惯性权重粒子群优化算法具备一定优势。除线性衰减惯性权重之外，也有人用指数递减衰减惯性权重替换线性惯性权重，使速度式再次发生改变。

(4)

式中:e-αE为指数递减惯性权重参数，αE为控制粒子搜索步长的参数。

1.3 NDPSO

本文通过改进参数设置原理推出正态分布衰减惯性权重策略，从而设计出NDPSO，并推出正态分布曲线衰减策略，用函数可记为：

(5)

式中:x为正态分布；μ为正态分布的位置参数，代表正态分布的集中趋势位置；θ为正态分布的趋势参数，代表正态分布资料数据分布的曲线趋势。

1.4 NDPSO算法设计

本文基于NDPSO，把ω用正态分布曲线给予衰减。在μ=0、θ=0.443 3时，正态分布曲线如图1所示。图1中：纵坐标f(x)为概率密度函数，表示随机变量x在连续区间内的函数输出值。

图1 正态分布曲线图(μ=0,θ=0.443 3)Fig.1 Normal distribution curves(μ=0,θ=0.443 3)

图1中:前期指的是随机变量处于[0,0.5);中期指的是随机变量处于[0.5,1);后期指的是随机变量处于[1,1.5]。由图1可知，算法在前期数值下调较快，中期完成快速衰减，后期逐渐趋于平缓。根据算法流程，算法在后期时，粒子用小步长进行局部开发(大步长可能会让算法粒子错过最优解)，直到算法结束。上述结果也说明惯性权重在粒子群算法中发挥了作用。

本文对图1进行分析后，将θ=0.443 3运用在标准粒子群优化算法中，得到新的ω非线性变化式：

(6)

式中:ωmax、ωmin分别为规定的最大上界惯性权重参数与最小下界惯性权重参数。

1.5 试验测试函数集

本文在12个测试函数中选取4个，以检测相关算法性能。测试函数里面有：单峰测试函数F1、F2、F3、F4、F5、F6、F13、F14；多峰测试函数F7、F8、F9、F10、F11、F12。记种群P规模为I；最大迭代次数为T；粒子位置定义域为[xmin，xmax]；粒子速度定义域为[vmin，vmax]；惯性权重定义域为[wmin，wmax]；rand产生伪随机数字。

F1是Sphere函数，解空间范围为[-100,100]D。F1测试式为：

(7)

式中:d为粒子维度，d=1,2,...,D。

F2是Quartic函数，解空间范围是[-1.28,1.28]D。F2测试式为：

(8)

F3是Rosenbrock函数，解空间范围是[-5,10]D。F3测试式为：

(9)

F4是Step函数，解空间范围是[-100,100]D。F4测试式为：

(10)

F5是Sum Squares函数，解空间范围是[-10,10]D。F5测试式为：

(11)

F6是Zakharov函数，解空间范围是[-5,10]D。F6测试式为：

(12)

F7是Ackley函数，解空间范围是[-32.768,32.768]D。F7测试式为：

(13)

F8是Rastrigin函数，解空间范围是[-5.12,5.12]D。F8测试式为：

(14)

F9是Griewank函数，解空间范围是[-600,600]D。F9测试式为：

(15)

F10是Schwefel函数，解空间范围是[-500,500]D。F10测试式为：

(16)

F11是Levy函数，解空间范围是[-10,10]D。F11测试式为：

(ωD-1)2[1+sin2(2πwD)]

(17)

(18)

F12是Powell函数，解空间范围是[0,π]D。F12测试式为：

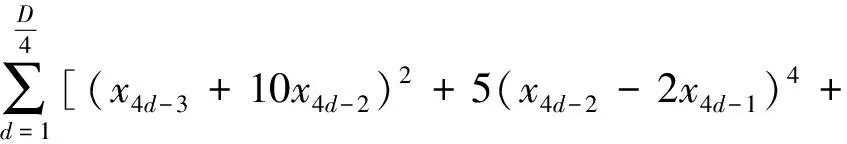
10(x4d-3-x4d)4]

(19)

F13是Dixon-price函数，解空间范围是[-10,10]D。F13测试式为：

(20)

F14是Sum Powers函数，解空间范围是[-1,1]D。F14测试式为：

(21)

1.6 试验设置

由于NDPSO惯性权重与正态分布曲线存在线性与非线性的区别，所以需要寻找到合适衰减机制的正态分布曲线。本试验将θ的值分别取0.2、0.4、0.443 3和0.5，并分别进行测试，从而获得最佳θ值。

NDPSO与其他改进粒子群优化算法能够作良好的能力比较。试验将引用单峰的F1、F2以及多峰的F7、F8测试函数对基于动态加速度系数的粒子群优化(particle swarm optimization based on dynamic acceleration coefficients,PSO-DAC)算法、惯性权重自适应粒子群优化(inertia weight adaptive particle swarm optimization,PSO-LH)算法这2个改进粒子群算法进行测试比较。这些算法是现阶段基于惯性权重或收缩因子进行改进的算法。试验规定种群P规模I=30、粒子维度N=30，学习因子C1和C2取 2，最大迭代次数T=1 000。测试函数都单独进行20次检验。出现的结果有最小值、平均值、标准差[15]。

2 研究结果

2.1 最佳正态分布的趋势分析

本文对θ取0.2、0.4、0.443 3、0.5，可以得到如图2所示的正态分布。

图2 正态分布图Fig.2 Normal distribution chart

图2中，前期指的是随机变量处于[0,0.5)，中期指的是随机变量处于[0.5,1)，后期指的是随机变量处于[1,1.5]。在算法迭代中：前期f(x)值较大，粒子用较大的步长进行搜索；后期f(x)值处于较低值的状态，粒子用小步长进行局部开发。由图2可知，x取0.3～0.4时，曲线坡度符合NDPSO的要求。通过观察与计算，当θ=0.443 3时结果最优。此时，曲线坡度与概率密度满足试验要求。

2.2 函数测试结果

本文利用F1和F2、F7和F8，分别对PSO-DAC、PSO-LH、NDPSO这3个算法进行测试。不同峰值下获得的函数测试结果如图3所示。

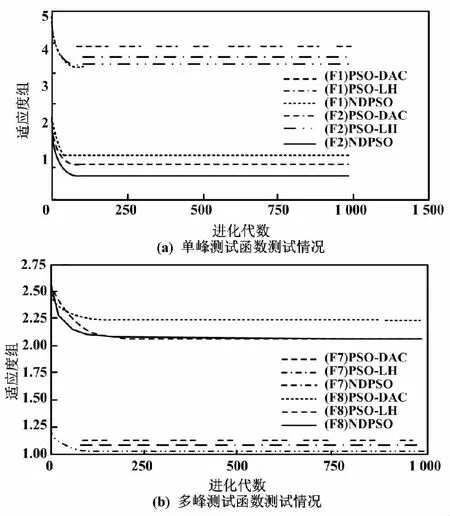
图3 不同峰值下获得的函数测试结果Fig.3 Results of function tests obtained at different peaks

根据F1、F2测试函数的自身特征，试验中规定的粒子维度是30。由图3(a)可知，PSO-DAC与PSO-LH收敛速度最佳，NDPSO紧跟其后。NDPSO的收敛精度优于其他改进算法。PSO-DAC与PSO-LH的收敛速度快，可能使算法在早期就达到了局部最优，因此两者的性能远远不如NDPSO。由图3(b)可知，NDPSO性能依然表现良好，算法的收敛速度与精度处于领先地位。因为多峰函数存在多个局部极值，寻优难度较高，也容易出现局部最优。而NDPSO的w衰减机制让算法前期的步长收敛，从而保证其不会陷入局部最优。在电力调度自动化评估的过程中，运用NDPSO可以提高神经网络模型处理复杂问题的能力，从设备状况信息中获取设备的状况特征，为找到最优解奠定基础，

2.3 标准测试函数的优化结果

F1、F2、F7、F8算法对使用标准测试函数的优化结果如表1所示。

表1 算法对使用标准测试函数的优化结果

由表1可知，NDPSO的最低值、均值与标准差都比较优秀。总的来说， NDPSO对速度与精度都有领先优势，能力相对更加出色。PSO-DAC与PSO-LH惯性权重机制没能最佳发挥w的作用，性能比NDPSO差一些。

3 结论

智能电网环境对电力调度自动化设备状态评估提出了新的要求。神经网络模型凭借其非线性处理能力在电力自动化设备评估中被广泛使用,然而其模型有匹配不到最优解、收敛速度慢的问题。针对此评估模型的优化，改进的粒子群算法成为了解决问题的突破口。本文在正态分布衰减惯性权重的基础上提出自适应变异优化策略，设计出NDPSO算法。该算法的惯性权重在前期保持较大的取值，使得粒子群算法在寻优时保持较大的步长；后期惯性权重保持较小的取值，并兼顾了全局搜索和局部开发的能力。算法仿真和结果分析证明，正态分布衰减惯性权重策略能够从参数改进角度平衡全局搜索和局部开发能力，在保证收敛精度的同时加快了收敛速度。改进的粒子群算法对神经网络模型具备一定优化能力，对电力调度自动化中设备的评估具有重要意义。不足的是，本文的仿真试验仅仅从单峰检测函数与多峰检测函数中挑选了部分函数进行检测。后续研究可就试验进行完善，让算法在其他检测函数中展现其性能。