基于IGG的特高压输电线路序参数抗差辨识方法研究

周 健,董晓岽,汪向军

(江苏省送变电有限公司,江苏 南京 210028 )

0 引言

特高压输电线路是特高压输电网进行传输的主要载体。其序参数可用于特高压网络的状态估计、故障分析及保护整定等，对特高压网络具有直接影响[1]。对于特高压输电线路序参数的测量不但存在时间限制紧、资金消耗大等问题，而且不准确的序参数测量将影响电网运行人员的决策，故危害性极大[2]。因此，有必要研究可靠、有效的方法，以实现特高压输电线路序参数在线抗差辨识。

当前，特高压输电线路序参数在线抗差辨识已成为备受关注的研究方向之一。国内外学者都在研究其输电线路参数及误差的运算。国外学者开展研究的时间较久，早在上世纪末期就开始使用同步测量测试输电线路的参数。近期，Asprou M等在2019年根据同步测量值估计传输线路参数的不确定性边界[3]。我国学者薛安成与孙怡等分别通过微型相量测量单元(phase measurement unit,PMU)和无迹卡尔曼滤波完成序参数在线抗差辨识[4-5]。这两种方法均能获得较好的在线抗差辨识效果。虽然上述方法都能对输电线路参数的误差进行估算，但受噪声、偏差等影响较大。因此，辨识精度和多时刻的辨识能力有待提高。

测量与地球物理研究所(Institute of Geodesy and Geophysics,IGG)提出的一种电力系统抗差估计方法被称为IGG法。该方法作为常用的等价权迭代法的权函数，可使用相应的权函数对多种情况的量测数据进行处理，从而提升量测信息的利用率。因此，本文提出了基于IGG准则的特高压输电线路序参数在线抗差辨识方法，以保障特高压输电网的安全、稳定运行。

1 基于IGG准则的抗差辨识方法

1.1 特高压输电线路相分量模型

使用相分量描述特高压输电线路，由IKφ表示K端φ相电流相量、UKφ表示K端φ相电压相量。其中，K的取值为M、N，φ的取值为a、b、c。相间互阻抗与相间互导纳分别用Zφφ、Yφφ表示，且φφ的取值为ab、bc、ca。每相串联阻抗与对地导纳分别用Zφφ、Yφφ表示。K端电压电流方程符合式(1)所示条件：

(1)

式中：YC为待辨识线路导纳矩阵；Z为待辨识线路阻抗矩阵[6]。

式(2)为将式(1)作进一步改写后所得结果：

(2)

待辨识参数用x=[x11x12...x19x21x22...x29]T表示。其在k时刻符合式(3)所示的线性方程：

Akx=Bk

(3)

式中：Ak为两端电压降的矩阵；Bk为电压与电流相量的矩阵。

从多时刻角度出发所得结果为：

(4)

根据式(5)的目标函数，可获得线路参数：

(5)

式中：vi为Ax-B。

1.2 获取序分量

正序(Fa(1))、负序(Fa(2))及零序(Fa(0))分量均为对称分量，能够通过唯一分解不对称分量获得。Fa、Fb、Fc用于表示不对称分量。Fa、Fb、Fc之间的关系用式(6)描述：

(6)

式中：α为算子，α=ej120°。

简化式(6)，可得：

Fp=TFS

(7)

式中：FS为A相电流或电压正、负、零序分量；Fp为三相电流或电压相量；T为对称分量法的变换矩阵。

设置线路每相互感阻抗与自感阻抗分别为zm、zs。根据电路理论[7-8]，三相电流、电压降在线路中符合式(8)所示条件：

ΔU=ZIM

(8)

依据式(8)，以序分量替换三相电流、电压降的结果为：

TΔUa=ZTIMa

(9)

综合上述分析，可得：

ΔUa=T-1ZTIMa=ZpIMa

(10)

式中：Zp为序分量的阻抗矩阵。

(11)

式中：za(1)为A相正序阻抗；za(2)为负序阻抗；za(0)为零序阻抗。

正、零序阻抗参数计算式为：

(12)

设置互导纳与对地导纳[9]为ym、ys，可得：

(13)

式中：yca(1)为A相正序导纳；yca(2)为负序导纳；yca(0)为零序导纳。

正、零序对地导纳参数计算式为：

(14)

1.3 三相不平衡数据

ε为三相电压不平衡度，定义为：

(15)

式中：F+为正序分量幅值；F-为负序分量幅值。

短时、负序电压不平衡度应分别低于4%、2%。这是公共连接点不平衡度在电网稳态运行时符合的条件。之所以能得到不平衡状况不同的实测PMU数据，是因为电网实际运行中，不同时段负荷的大小、类型存在差异[10-11]。

1.4 基于自适应抗差最小二乘的辨识

1.4.1 抗差最小二乘基本原理

(16)

1.4.2 IGG抗差法

为提升量测信息的利用率，本文通过IGG抗差法将量测信息分为正常、可利用、有害量测。对于各类别的量测信息，利用对应的权函数进行处理[12]。IGG抗差法的权函数为：

(17)

式中：k、r为抗差阈值的调制系数；vi为第i个量测的残差；σ0为量测误差标准差。

IGG极值函数为：

(18)

1.4.3 残差分布的自适应估计

IGG权函数应选取合理的抗差阈值，以确保抗差辨识方法的抗差能力、提高辨识结果的准确性。抗差阈值由量测误差的标准差决定。由于量测误差具有多变性，需提出残差分布的自适应估计，以提升抗差辨识方法的适应能力。根据中位数原理对残差序列的期望与标准差进行估计，估计结果如式(19)、式(20)所示。

(19)

式中：v为残差序列；median(v)为中位数。

(20)

对残差序列分布进行有效估计后，更新后的IGG抗差法的权函数为：

(21)

2 试验结果分析

本文以某特高压输电线路作为试验对象，从中获取不平衡时的PMU数据，并选择600组稳态后的数据实施在线抗差辨识。在试验过程中，各序参数用X表示，量测误差不存在时序参数的在线辨识结果如图1所示。分析图1可知，当量测误差不存在时，序参数的实际辨识值与设定值几乎完全一致。该结果说明本文方法具有较好的特高压输电线路序参数在线辨识效果，且辨识准确性高。

图1 量测误差不存在时序参数的在线辨识结果Fig.1 Online identification results of timing parameters without measurement errors

试验设置在PMU数据中增加0.3%强度的噪声，以及20%的偏差，分析量测误差存在时的序参数在线抗差辨识效果，并设计对比试验。选择文献[4]的微型PMU方法与文献[5]的无迹卡尔曼滤波方法与本文方法进行对比测试。误差存在时序参数在线抗差辨识相对误差如表1所示。分析表1可知，当量测误差存在时：微型PMU方法的辨识相对误差较低，最低为0.65%、最高为5.36%，偏离实际结果的程度较小；无迹卡尔曼滤波方法的辨识相对误差较高，最低为1.21%、最高达11.86%，与实际结果偏离程度较大；本文方法的辨识相对误差始终不超过0.4%，与实际结果最接近。对比这些数据可知，本文方法具有极强的抗差能力，序参数在线抗差辨识效果优势明显，无迹卡尔曼滤波方法的辨识结果可信度最低。

表1 误差存在时序参数在线抗差辨识相对误差

试验分析量测误差不存在时，3种方法在不同电压不平衡度下序参数在线抗差辨识结果如图2所示。

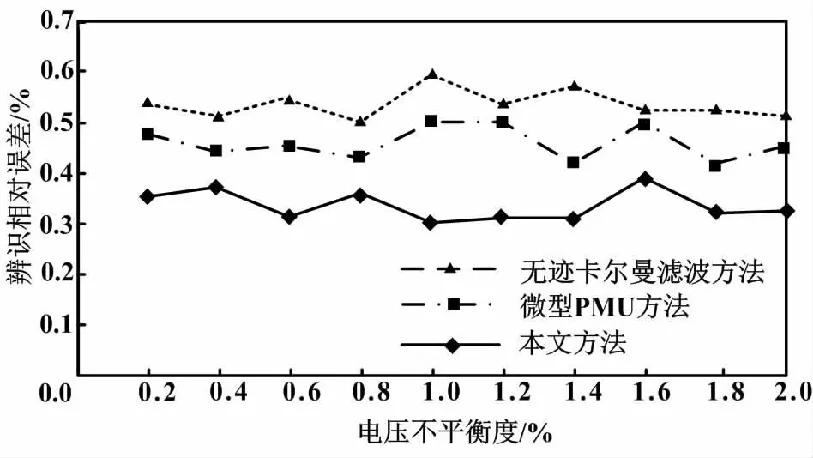
图2 不同电压不平衡度下序参数在线抗差辨识结果Fig.2 Online anti-differential identification results of sequence parameters under different voltage unbalance degrees

分析图2可知，当量测误差不存在时，3种方法的辨识相对误差比较接近，均无明显波动，但本文方法的辨识相对误差始终低于其他两种方法，且波动最小。由此可以说明，在量测误差不存在的情况下，3种方法的辨识结果基本不受电压不平衡度的影响。综合以上2个试验结果可得，在多种情况下，本文方法均能展现出较优异的序参数在线抗差辨识效果，能有效防止量测误差的干扰，性能优越。

3 结论

本文提出了基于IGG准则的特高压输电线路序参数在线抗差辨识方法。经试验验证，该方法的序参数实际辨识值与参数设定值基本一致，具有较高的序参数在线辨识精度。该方法能有效抵抗量测误差的干扰，在多种情况下具有较优异的序参数在线抗差辨识效果，且辨识结果可信度高，可为特高压输电网的安全稳定运行提供科学、准确的数据支持。