青海尕沙日特大型滑坡稳定性评价
贾升安 李春阳 段顺荣
1 青海省水文地质及地热地质重点实验室,西宁市苏家河湾4号,810008 2 青海省水文地质工程地质环境地质调查院,西宁市苏家河湾4号,810008 3 青海省核工业地质局,西宁市新宁路2号,810008
滑坡的稳定性直接关系到防治措施的设计,因此滑坡的稳定性评价至关重要[1-5]。实际工程中常用传递系数法[6]计算滑坡稳定性。根据田成成等[7]的研究成果,尖点突变分析可用于滑坡的稳定性评价。变形预测能较好地反映滑坡变形的发展趋势,可用于滑坡稳定性发展趋势的评价。本文以青海尕沙日特大型滑坡为工程背景,首先通过传递系数法开展常规滑坡稳定性分析,然后进行尖点突变分析和滑坡变形预测。
1 基本原理
1.1 常规稳定性模型
传递系数法是GB/T 32864-2016《滑坡防治工程勘查规范》规定使用的滑坡稳定性计算方法,具有操作简单、实用性强等优点。结合滑坡实际,将滑坡稳定性的计算工况分为3种类型:1)自重工况,即仅对滑坡自重进行稳定性计算;2)自重+暴雨工况,即考虑暴雨条件下的滑坡稳定性;3)自重+地震工况,即考虑地震条件下的滑坡稳定性。根据计算得到的稳定系数Fs可进行滑坡稳定状态划分:Fs<1为不稳定状态、1≤Fs<1.05为欠稳定状态、1.05≤Fs<1.15为基本稳定状态、Fs≥1.15为稳定状态。
1.2 稳定性佐证模型和发展趋势评价模型
考虑到滑坡变形是其稳定性的量化体现,因此以滑坡变形监测成果为基础,利用尖点突变理论和变形预测思路来构建滑坡稳定性佐证模型及发展趋势评价模型。
1.2.1 稳定性佐证模型
尖点突变分析可通过数学模型来评价连续行为中的突发质变过程,在岩土领域已得到广泛应用。尖点突变分析过程中,标准函数V(t)为:
V(t)=t4+qt2+pt
(1)
式中,q、p为拟合参数,t为时间变量。以滑坡变形监测数据为基础对式(1)进行拟合处理,可得到参数q、p,进一步计算得到突变特征值Δ:
Δ=8q3+27p2
(2)
通过Δ的大小可判断滑坡稳定性:若Δ>0,说明滑坡大概率处于稳定状态;若Δ=0,说明滑坡处于临界稳定状态,具有波动性;若Δ<0,说明滑坡大概率处于不稳定状态。
1.2.2 稳定性发展趋势评价模型
一般情况下,滑坡变形越大,其稳定性相对越弱。若滑坡后续变形处于增加趋势,其稳定性也将随之减弱;相反,若滑坡后续变形趋于稳定,其稳定性将会维持现状。因此可通过变形预测来评价滑坡变形的后续发展情况,并进一步评价滑坡稳定性的发展趋势。
NARX神经网络能够在线性输入条件下进行非线性输出,具有较强的普适性,因此可利用其构建滑坡变形预测模型,基本原理见文献[8-10]。但NARX神经网络的延迟阶数及隐层节点数多由使用者确定,缺乏客观性,因此有必要对其进行优化处理。天牛须搜索(beetle antennae search,BAS)具有参数简单、计算简便等优点,可利用其实现NARX神经网络的参数优化。BAS-NARX神经网络的构建步骤为:
1)输入数据。对变形数据进行归一化处理,运行得到初步估计值,然后将其作为闭环NARX神经网络的输出量。
2)初始化参数。对BAS算法的参数进行初始化设置,如设置步长、随机向量及待优化参数等,然后对天牛初始位置进行设置。
3)确定适应度函数。对闭环NARX神经网络进行初步训练,并对初步预测结果进行筛选,确定最优适应度函数值至最优位置处。
4)迭代寻优。不断更新天牛范围及其位置,并计算相应的适应度函数值,将其与最优位置处的适应度值进行对比,实现寻优参数的更新迭代。
5)判断迭代是否结束。当达到最大迭代次数或期望目标时,停止迭代;否则,增加搜索步长,继续迭代寻优。
6)输出参数。当满足迭代结束条件后,输出最优适应度函数对应的寻优参数,即可得到最优的延迟阶数及隐层节点数。
虽然BAS算法的优化处理保证了NARX神经网络参数的最优性,但也难以完全刻画出滑坡变形的非线性特征,即BAS-NARX神经网络的预测结果仍会存在一定误差。为此,需再对其预测误差进行弱化处理。
根据文献[11]可知,ARIMA模型具有较强的误差弱化能力,误差弱化过程可表示为:
(3)
式中,zt为误差弱化值,φm为自回归参数,k、l为回归阶次,at为白噪声,θj为滑动参数。进行ARIMA模型的误差弱化处理后,得到最终滑坡变形预测模型BAS-NARX-ARIMA。
2 实例分析
2.1 工程概况
尕沙日滑坡的平面为半圆形,主滑方向为111°,纵向长度约2 160 m,宽度约910 m,厚度为65~75 m,体积约13 759.2×104m3,属特大型滑坡(图1)。滑坡主滑面具有折线特征,发育有二级平台;二级平台位于滑坡后缘,纵向长度约200 m,横向延伸宽度约1 000 m,平台后缘的滑坡壁明显,高约100 m;一级平台位于滑坡中部,纵向长度约150 m,宽度约500 m,坡度小于8°。同时,滑坡两侧冲沟发育明显,具有“V”型特征,多为季节性流水所致,侵蚀深约5~10 m,宽约10~20 m。
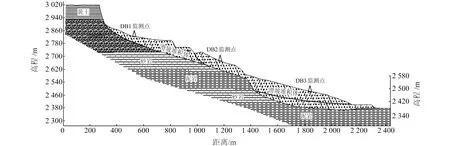
图1 主滑面地质剖面Fig.1 Geological profile of main sliding surface
根据钻探成果,对滑坡结构地层分述如下:滑体土为黄色或褐红色,岩性为含砾粉土、黄土等,土质松散且不均匀,厚度变化差异大,主要为65~75 m;滑带土为褐红色,岩性为粉质粘土,岩芯可见挤压层理,并呈鱼鳞片状,含水量较高,埋深65~80 m,平均埋深约70 m,层厚0.5~2.6 m;滑床为褐红色,岩性主要为强风化泥岩,泥质结构,层状构造,以粘土矿物为主,揭露厚度8~11 m。
结合现场调查成果,按照变形分布位置,将滑坡变形破坏特征总结如下:
1)后缘变形特征。形成规模不一的下错陡坎,并伴随形成洼地及鼓丘。其中,洼地多呈椭圆状,轴长270~600 m,深度3~5 m;鼓丘相对高差15~20 m,坡度30~40°。
2)中部变形特征。以洼地和鼓丘为主,但规模与后缘具有一定差异。其中,洼地为椭圆形平面,轴长约230~310 m,深度2~5 m;鼓丘相对高差10~20 m,坡度15~20°,相对后缘较平缓。
3)前缘变形特征。以陡坎为主,坎高约6 m,坡度60°~70°。
2.2 常规稳定性评价
利用传递系数法对主滑面进行稳定性计算,结果见表1。

表1 常规稳定性计算结果Tab.1 Conventional stability calculation results of landslide
由表1可见,工况3的稳定性相对最差,工况1的稳定性相对最好,说明尕沙日滑坡是自重+地震工况;工况1和工况2之间的稳定系数相差不大,这是因为尕沙日滑坡的滑体厚度较大,降雨及其入渗时间相对较短,故2个工况的抗滑参数一致,但工况2将降雨入渗范围内的土体重度改成了饱和重度。
2.3 稳定性佐证评价和发展趋势分析
在主滑面布设3个监测点DB1、DB2、DB3(图1),共监测30个周期,所得变形值为监测点的总位移值,得到滑坡变形时间曲线(图2)。由图2可见,滑坡变形持续增加,其中,DB2监测点的变形量相对最大,DB1次之,DB3相对最小,说明滑坡中部变形相对最大,其次是后缘,前缘变形相对最小。
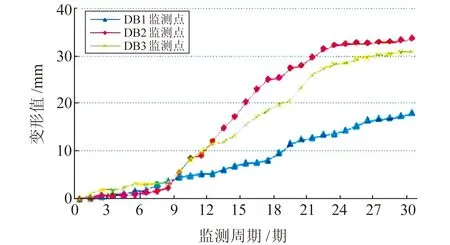
图2 滑坡变形时间曲线Fig.2 Deformation time curve of landslide
2.3.1 稳定性佐证分析
对3个监测点进行尖点突变分析(表2)。由表2可见,在标准函数的拟合过程中,3个监测点的拟合度区间为0.958~0.970,变化范围相对较小,且均趋近于1,说明后续尖点突变分析结果准确、可靠。3个监测点的Δ范围为(3.673~4.099)×109,均大于0,说明3个监测点均处于稳定状态,佐证了上述常规稳定性计算结果的准确性。根据Δ大小可知,DB1监测点的稳定程度相对最高,其次是DB3和DB2。

表2 尖点突变分析的稳定性结果Tab.2 Stability results of cusp mutation analysis
为进一步掌握滑坡稳定性随时间的变化规律,将滑坡监测样本划分为3个阶段,每个阶段递增10个周期的数据,并对每个阶段监测样本进行尖点突变分析(图3)。由图3可见,各监测点在不同阶段的Δ存在一定差异,Δ随时间持续减小,即滑坡稳定性随时间持续减弱,且阶段1到阶段2的减小值要明显大于阶段2到阶段3的减小值,说明滑坡稳定性在监测前期的减小程度更大。

图3 滑坡变形时间曲线Fig.3 Deformation time curve of landslide
综上所述,尕沙日滑坡处于稳定状态,与常规稳定性分析结果一致,只是不同位置处的稳定程度有一定差异,且滑坡稳定性随时间持续减弱。
2.3.2 稳定性发展趋势分析
利用变形预测开展滑坡稳定性发展趋势分析。若滑坡变形趋于收敛,则滑坡稳定性将维持现状;若滑坡变形持续增加,则滑坡变形将趋于减弱。将1~25期的数据作为训练集,26~30期的数据作为验证集,后续外推预测4个周期。同时,为充分验证BAS算法的优化效果及ARIMA模型的误差弱化能力,以DB1监测点为例,给出NARX、BAS-NARX和BAS-NARX-ARIMA模型的预测效果(表3)。由表3可见,BAS算法在相应验证样本处对NARX神经网络进行优化处理后,BAS-NARX模型的MSE值、MAPE值和CT值均出现不同程度的减小,验证了BAS算法的优化效果。经过ARIMA模型的误差弱化处理后,BAS-NARX-ARIMA模型的3个评价指标值均较BAS-NARX模型进一步减小,证明了ARIMA模型具有较强的误差弱化能力。综上可知,BAS算法和ARIMA模型对NARX模型的优化处理不仅能提高预测精度,还能有效节约收敛时间,充分说明BAS-NARX-ARIMA模型适用于滑坡变形预测。

表3 3种模型在DB1监测点的预测结果Tab.3 Prediction results of three models at DB1 monitoring point
对其余2个监测点进行预测及外推预测(表4)。由表4可见,3个监测点的MSE为0.07~0.49 mm2,MAPE为2.03%~2.11%,CT为69.38~73.98 ms,3个评价指标值均较小,且变化范围也较小,进一步说明BAS-NARX-ARIMA模型具有较强的稳健性。根据外推预测结果可知,滑坡变形量会持续变大,且外推预测周期的增加速率相较26~30周期的增长速率并无明显减小趋势,得出滑坡稳定性仍会持续减弱。

表4 各监测点的预测结果Tab.4 Prediction results of each monitoring point
3 结 语
1)通过传递系数法的常规稳定性评价,得出滑坡在3种工况条件下的稳定系数Fs为1.148~1.697,属于基本稳定或稳定状态,且最不利工况为自重+地震工况。
2)通过尖点突变分析可知,各监测点的Δ均大于0,即均处于稳定状态,佐证了常规稳定性计算结果的准确性,但不同位置处的稳定性程度存在一定差异,且滑坡的稳定性随时间持续减弱。
3)通过变形预测分析可知,BAS-NARX-ARIMA模型在滑坡变形预测中展现出较好的稳健性,预测效果良好;滑坡变形量会持续增加,稳定性也会进一步减弱。
本文基于滑坡变形监测成果开展滑坡稳定性评价,未来可结合滑坡所处地质条件,进一步利用数值模拟评价滑坡稳定性,以确保稳定性分析结果的准确性。

