FLOW-3D气泡流模型关键参数敏感性探究

董宗师，蔡 芳

（1.长江设计集团，湖北 武汉 430010；2.四川大学水利水电学院，四川 成都 610065）

0 引 言

流动掺气尤其是水面自掺气在明渠、溢洪道、水工隧洞等引水、输水、泄水建筑物中非常常见，对工程的安全运行有着重要的影响［1-3］。具体而言，掺气会增加流道中的水深［4-6］，影响射流的冲刷效果［7］，还可以影响坝下鱼类等水生生物的生存环境［8-10］；同时，结构面附近的气泡对减免高速水流的空蚀破坏也有着至关重要的作用［11，12］。当前，对于工程水力学的研究多依据重力相似准则而采用模型试验的方法，但在掺气水流中表面张力和黏性力的作用明显，因此，试验研究成果与工程实际相比存在较为明显的比尺效应［13］。原型观测也存在成本高、测量参数有限、仪器结构强度不足等缺点［14］。而随着计算机算力的飞速提升和计算物理学的快速发展，计算流体力学（CFD）在工程水力学研究中得到了越来越广泛的应用。

相比带有自由面的单相流模拟，掺气水流的模拟要复杂的多，需要附加自由水面掺气、气泡尺寸计算、水-气相对速度估计、两相湍流模拟以及气泡的变形、破碎及聚合等多种其他模型［15］。目前，Ansys Fluent 和OpenFOAM 等流行的CFD 软件中虽然含有多个气∕液、气∕固、液∕固多相流曳力和湍流模型，但无法考虑界面处的湍流掺气，也就无法完成对于掺气水流的模拟［16，17］。近年来，多个学者使用FLOW-3D 软件对台阶［18］、宽尾墩［19］、明渠［20］等泄水建筑物中的掺气水流进行了数值模拟，开创了在泄洪模拟中考虑掺气作用的先河。然而，FLOW-3D 软件官方文档中并未对以下模型细节进行说明，限制了用户对软件参数的选择和准确性分析。①在计算气泡直径时采用的模型方程；②临界毛细管数中的参数含义以及临界韦伯数和临界毛细管数对于不同流动的主导作用；③初始气泡直径的取值建议以及其通过何种方式影响计算结果。此外，模型中含有两个重要的参数——拖曳系数以及Richardson-Zaki 调节系数，虽然软件给出了默认值，但其对计算结果的影响也不明确。本文对FLOW-3D 掺气流模型中临界毛细管数、临界韦伯数、气泡初始直径、拖曳阻力系数以及Richardson-Zaki 调节系数等模型参数对计算结果的影响进行了敏感性分析，以供相关的数值模拟参考。

1 研究对象与模型设置

1.1 研究对象

本文选取了Straub & Anderson 的明槽均匀流试验［21］中45°坡度下流量为0.269 m3∕s 的工况为验证算例。试验中所使用的明槽宽和高分别为0.45 m 和0.3 m，长度为15 m，槽底平均突起高度为0.71 mm。在模拟中，忽略了两侧边墙的影响将展向网格设置为1 进行二维模拟。同时，为了保证水流达到均匀流状态，将泄槽长度延长至50 m，并在x=48 m 处进行数据采集。计算体型和设置示意见图1。

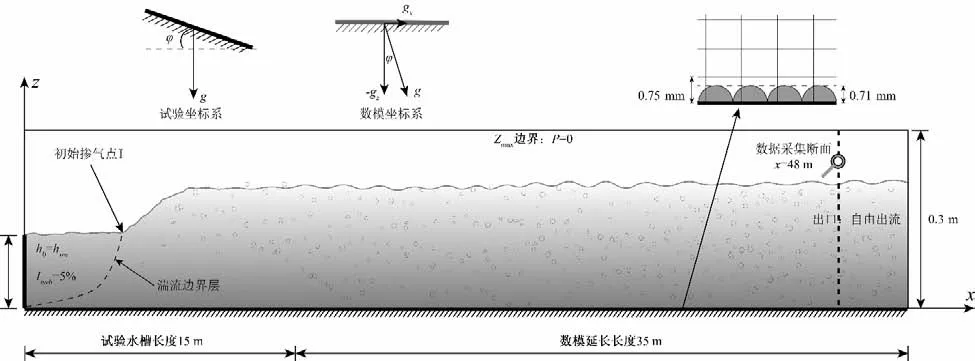
图1 计算体型与设置示意图Fig.1 Schematic diagram of simulated geometry and simulation setup

1.2 模拟设置

在计算中，为了保证FAVOR 界面捕捉技术对槽底的解析精度，明槽与x轴平行（即水平）放置，并根据明槽45°坡度来调整重力分量，流向和垂直槽底向下的重力加速度均为6.937 m∕s2。计算使用了均匀的结构化网格，单元尺寸为Δx=0.017 m，Δz=0.025 m，并将槽底第一层网格高度设置为0.75 mm 以保证壁面函数计算湍流参数的准确性（实际计算得到的槽底y+值为97）。计算域边界条件设置如下：底部设置为无滑移固壁边界，顶部给定零压边界，进口根据流量和相同水力条件下的均匀流水深h0=0.049 m 给定均匀流速边界，并假定湍流强度为5%，出口则设置为自由出流。所有计算结果均在计算域内水体的总体积变化率小于0.5%时采集。

2 数学模型

FLOW-3D 软件因其特有的Tru-VOF 自由面追踪方法而在水利水电、港口工程等领域得到了广泛的应用。Tru-VOF 方法在每个时间步完成自由水面追踪之后，即将空气区域移出计算区域而只对壁面和水面围成的水体进行计算。这种技术依赖于对壁面和水面处施加恰当的边界条件［22］。而对于湍流的模拟，考虑到所模拟流动的高雷诺数而采用了RNGk-ε湍流模型。对气泡流的模拟则使用了表面掺气模型、变密度模型、漂移流模型、气泡尺度模型等系列模型来实现。上述模型相应的方程如下。

2.1 纳维-斯托克斯方程组

式中：u为流速；f为体积力；ρ和υ分别为水的密度和运动黏度系数。

2.2 湍流模型

式中：k为湍动能，ε为湍动耗散率；Pk为由于平均运动梯度引起的湍动能产生项；Deffk和Deffε分别为k和ε的扩散系数，其计算方法及其他常数的取值详见文献［15］。

2.3 表面追踪模型

式中：f为水的体积分数；Sa为掺气源项［详见公式（9）］；Vc为网格单元体积。

此方程为一纯对流方程，为了避免产生数值扩散，FLOW-3D采用施主-受主技术来几何求解和重构界面。

2.4 表面掺气和逸出模型

FLOW-3D 中的掺气模型［23］假设掺气的发生是由于湍动能在垂直水面的分量大于表面张力和重力两个抗力，其控制方程为：

式中：LT为湍流特征长度；gn是重力在水面法向的分量；σ为表面张力系数，计算时取0.073 N∕m；Sa为掺气速率；ka为一用户定义的系数，默认值为0.5；As为水面处网格内水面的面积，湍流模型常数Cμ=0.085。

FLOW-3D 还允许气泡从水面逸出，其实现方法为用户可以定义一个最大掺气浓度cmax，当水面处的掺气浓度大于cmax时会被重新设定为cmax。

2.5 变密度模型

变密度模型用以考虑掺气引起的流体密度变化。掺入的气泡与水体的相对运动可被抽象为掺气浓度的对流-扩散方程：

式中：c为掺气浓度；Ua为气相的速度；Dc为掺气扩散系数；Sa为式（5）和式（9）中的掺气源项；Vc为各网格单元的总体积。

掺气水流的宏观密度则直接计算为体积平均：

式中：ρw和ρa分别为水和空气的密度；c为掺气浓度；ρ为两相流的平均密度。

2.6 漂移流模型

浮力、水-气间相对运动的阻力和其他相互作用通过漂移流模型来模拟［24，26］。考虑到水体和空气的密度相差近1 000倍，FLOW-3D 中假定水-气滑移在极短时间内达到平衡，因此相间的滑移速度可通过下式进行计算：

式中：K基于网格单元的阻力系数；ur为水-气间的滑移速度；K的值通过单气泡的阻力系数Kp来计算：

式中：Ap为单个气泡的截面积；Ur为ur的模；ρc和μc为连续相（在本文中为水）的密度和动力黏度；Vp为单个气泡的体积；Rp为气泡半径；Cd为用户定义的拖曳系数，默认值为0.5。

当掺气浓度较高时，网格内气泡量较多，此时还需要考虑气泡间的相互作用对滑移速度的影响，FLOW-3D 采用文献［25］中的修正公式来考虑这一影响：

式中：CRZ为Richardson-Zaki调节系数，软件推荐其值为1（即不进行调节修正）；ζ为Richardson-Zaki 系数，其值与水流的流动状态有关，可通过气泡雷诺数Reb计算。当1 ＜Reb≤ 500 时ζ=4.45∕Re0.1b，当Reb＞500时，ζ=2.39。

在计算中，可将气泡直径设为定值或由程序根据流动状态计算。FLOW-3D 中使用临界韦伯数和临界毛细管数来估计气泡的尺寸［26］，计算时采用的方程如下：

式中：μm为混和相的分子动力黏度；μt，m为混和相的湍流动力黏度；由量纲分析可知，e的量纲为［T-1］。但官方文档和相关文献并未对其进行说明。考虑到此值与湍流相关，因此在本文中取为湍流时间尺度的倒数。

如上文所述，模型中有若干用户自定义参数。气泡半径采用动态计算，这些参数的默认值如下：临界韦伯数Wec=1.6，临界毛细管数Ca，c=1，拖曳系数Cd=0.5，Richardson-Zaki 调节系数Crz=1。在计算中，水体的体积分数范围设定为0.1～1，即当掺气浓度高于90%时会被自动设置为90%。空气的密度和黏度分别取为1.225 kg∕m3和1.7×10-5kg∕（m·s），且水相被一直认为连续相。

3 计算成果与分析

3.1 气泡尺寸的主要控制参数

如上文所述，FLOW-3D 中的气泡尺寸模型主要通过临界韦伯数Wec、临界毛细管数Ca，c和气泡聚合模型来实现，但未给出上述参数的阈值和模型方程。这些细节直接影响了气泡的大小，对于算例的设置非常重要。虽然在软件中并未直接提供韦伯数和毛细管数的值，但可以通过一定的方法进行二次计算。在均匀流区域（即本文的数据采集断面），流向的压强梯度与垂向相比可以忽略，因此可据式（12）～（17）计算韦伯数和毛线管数的值：①根据z 向压强梯度、掺气浓度c和气泡直径db通过式（12）～（14）求得滑移速度Ur；②根据式（15）对Ur进行修正得到Ueff r；③根据Ueff r用式（16）和（17）计算得到We和Ca。图2展示了用上述方法计算得到的毛细管数和韦伯数，其中蓝色实线为软件默认值。

图2 x=48 m断面上的毛细管数和韦伯数垂向分布Fig.2 Vertical distribution of Capillary number and Weber number at x=48 m

由图2可见计算得到的毛细管数和韦伯数与设定值均有一定差别。毛细管数的计算值在水体中部为一恒定值，且仅比设定值大15%左右，但算得的韦伯数与设定值则有着显著差别，虽然在水面处较为接近，但在底部相差9 个量级。由此可见，FLOW-3D 的气泡流模型中对于明渠这种强紊动掺气水流，气泡尺寸主要是受临界毛细管数控制。从物理作用机理的角度来看，因为湍流对气泡破碎的作用强于水-气间的惯性力，因此这一算法是合理的。至于毛细管数计算值与设定值的差别，则于滑移速度修正、湍流黏度计算等因素均有一定关系，由于这些均为软件的黑匣子细节，因此难以进一步定论。

3.2 临界毛细管数的影响

为了进一步考察FLOW-3D 掺气水流特性计算结果对临界毛细管数Ca，c的敏感性，分别将Ca，c取为1、2、4 三个不同的值探进行模拟探究。图3展示了3个Ca，c取值下的湍动能、湍流时间尺度以及湍流黏度的计算结果。由图3可见在不同的Ca，c下湍动能、湍流时间尺度以及湍流黏度的垂向分布曲线几乎完全重合，表明将临界毛细管数提高至默认值的4 倍对水流的湍流特性没有影响。

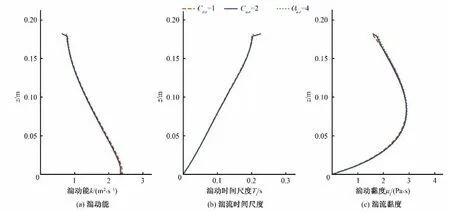
图3 3种临界毛细管数下的湍动能、湍流时间尺度和湍流黏度Fig.3 Turbulent kinetic energy，turbulent time scale and turbulent viscosity under three critical capillary numbers

图4展示了Ca，c分别设定为1、2、4 时计算得到的掺气浓度、气泡直径、滑移速度及毛细管数。从式（17）来看，对于本文模拟的强烈紊动的明渠水流，相比湍流黏度而言分子黏性可以忽略不计。因此，在同一湍流时间尺度下，气泡直径与临界毛细管数线性相关。然而，本文测试的3 个最大相差4 倍的临界毛细管数所得到的气泡的直径相差不大，同时增加临界毛细管数使滑移速度和毛细管数也小幅增加。这主要是由于气泡聚合作用强于临界毛细管数的影响，使临界毛细管数对计算结果的影响并不明显。

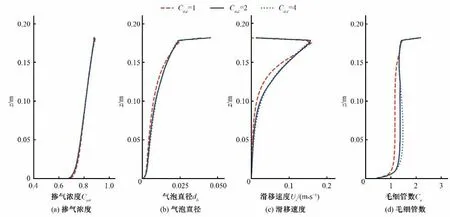
图4 3种临界毛细管数下的掺气浓度、气泡直径、滑移速度和毛细管数Fig.4 Air concentration， bubble diameter，slip velocity and capillary number under three critical capillary numbers

3.3 临界韦伯数的影响

本节对计算结果对临界韦伯数Wec值的敏感性进行探究。在FLOW-3D 中，Wec的默认值为1.6，本文将其值分别取为3.2和6.4来考察Wec对计算结果的影响。类似地，从图5可见，将临界韦伯数Wec取为默认值的2倍和4倍并不会对湍动能、湍流时间尺度以及湍流黏度等湍流特性产生显著影响。

图5 3种临界韦伯数下的湍动能、湍流时间尺度和湍流黏度Fig.5 Turbulent kinetic energy，turbulent time scale and turbulent viscosity under three critical Weber numbers

图6展示了3 种Wec值下的掺气浓度、气泡直径及韦伯数的计算结果。可以发现增大临界韦伯数会略微降低底部掺气浓度，同时使水面附近掺气浓度小幅增加，即使掺气浓度的垂向差别更大。进一步观察气泡尺寸的分布可知这是因为较大的临界韦伯数的值使气泡尺寸分布更广，将Wec变为默认值的2倍和4倍后水面气泡尺寸从4 cm 变为7 cm 和9 cm。综上所述，临界韦伯数对计算的影响也较小，但略大于比临界毛细管数的影响。

图6 3种临界韦伯数下的掺气浓度、气泡直径及韦伯数Fig.6 Air concentration，bubble diameter and Weber number under three critical Weber numbers

3.4 气泡初始直径的影响

在FLOW-3D 软件中，对掺气水流进行计算时需在漂移流子模型中指定初始气泡直径，但相关的模型方程［即方程（5）～（17）］中并未出现气泡初始直径这一参数，考虑到气泡直径由软件中相关模型自动计算，初步判断此值对计算结果没有影响，本节主要对此进行验证。类似地，图7和图8分别展示了1、5 和10 mm 三种初始气泡直径d0下计算的湍流特性和气泡特性，显然3种不同的d0下各参数的计算结果几乎是相同的，表明初始气泡直径确实对计算结果没有任何影响。

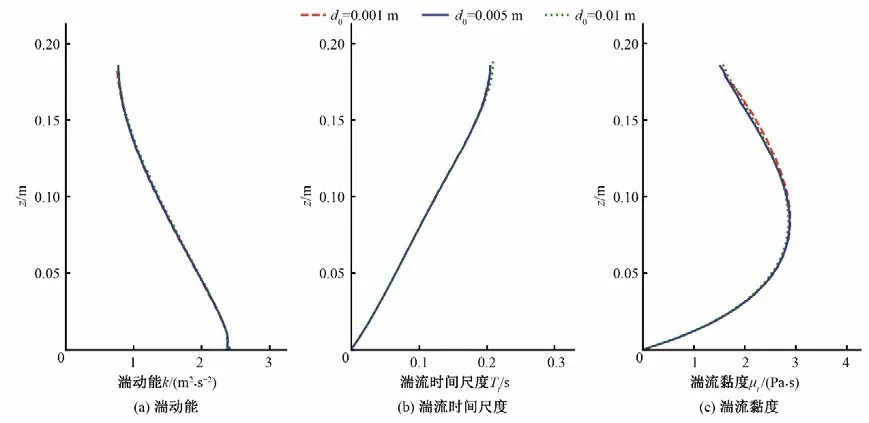
图7 不同初始气泡直径d0下的湍动能k、湍流时间尺度Tt以及湍流黏度μt分布Fig.7 Distribution of turbulent kinetic energy k，turbulent time scale Tt and turbulent viscosity μt under different initial bubble diameter d0

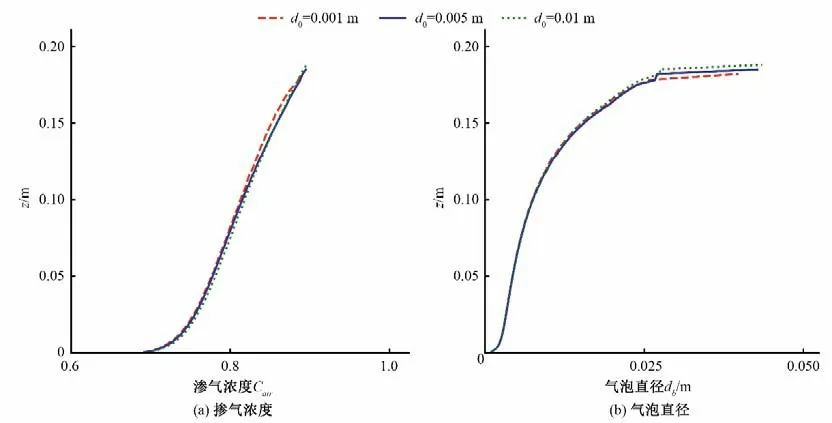
图8 不同初始气泡直径d0下的掺气浓度Cair和气泡直径dbFig.8 Calculated air concentration Cair and bubble diameter db under different initial bubble diameter d0

3.5 拖曳系数的影响

从水-气细观物理作用机理上来看，水-气间的拖曳作用与水流流态、气泡形状及大小等均密切有关。在FLOW-3D 的掺气水流模型中，拖曳系数也对水-气间的滑移速度和水流中的掺气浓度有着重要影响，其默认值为0.5。由式（13）可以发现，FLOW-3D 在计算两相拖曳力时，除了拖曳系数线性项CdUr外，还包含了气泡雷诺数的相关项同时，考虑到一般认为在湍流流态中单独使用CdUr计算拖曳力时Cd取值在2.67左右，本文将Cd分别取值为0.1、0.5、1、1.5 和2.67 五个值来考察拖曳系数对计算结果的影响，结果如图9和10所示。

由图9可以发现，拖曳系数Cd对湍流特性的影响较为显著。随着Cd增大，掺气水流的湍动能也有所增加，湍流黏度则表现为在下半部分减小，上半部分增加，但Cd对湍流时间尺度的影响不明显。而且，将Cd设为比默认值0.5 更大的值比使用较小的值对结果的影响要小。从图10可见，将拖曳系数由默认值0.5 减小至0.1 时，掺气水深由0.2 m 降低了30%，底部掺气浓度由70%下降到了40%；而增大Cd直至2.67对掺气浓度和气泡直径的垂向分布没有太大影响，只使掺气浓度和掺气水深小幅增加，对气泡直径的影响也仅体现在上部水体内。因此，拖曳系数对于计算结果的影响较为显著，将其默认值定为0.5 是合理的。

图9 不同拖曳系数Cd下的湍动能k、湍流时间尺度Tt以及湍流黏度μt分布Fig.9 Distribution of turbulent kinetic energy k，turbulent time scale Tt and turbulent viscosity μt under different drag coefficient Cd

图10 不同拖曳系数Cd下的掺气浓度Cair和气泡直径dbFig.10 Calculated air concentration Cair and bubble diameter db under different drag coefficient Cd

3.6 Richardson-Zaki调节系数的影响

FLOW-3D 的气泡流模型通过一个乘数Crz对Richardson-Zaki 系数进行线性调节来模拟气泡聚合对滑移速度的影响。由式（15）可知，Ur的修正项为一底小于1的指数函数，因此当Crz＞1 时将减小滑移速度，反之亦然。图11和图12分别展示了3个不同的Crz值下计算得到的湍流特性和气泡特性。由图11和图12可以发现计算结果对Crz较为敏感：小于1的Crz对会降低湍流程度并减弱掺气，反之亦然；将Richardson-Zaki 调节系数Crz由默认值1降低至0.5对计算结果有着明显影响：槽底掺气浓度从70%下降43%至40%左右，但Crz对气泡直径的影响主要体现在上部区域，这与拖曳系数Cd对气泡大小的影响是相似的。相比之下，将Crz提高至1.5 使滑移速度减小，湍流强度升高，进一步增加了掺气。总体而言计算结果对Richardson-Zaki 调节系数Crz是较为敏感的。

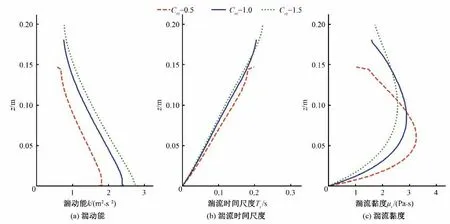
图11 3种Richardson-Zaki调节系数下的湍动能、湍流时间尺度和湍流黏度Fig.11 Turbulent kinetic energy，turbulent time scale and turbulent viscosity under three Richardson-Zaki coefficient multiplier values

图12 不同Richardson-Zaki调节系数Crz下的掺气浓度Cair和气泡直径dbFig.12 Calculated air concentration Cair and bubble diameter db under different Richardson-Zaki coefficient multiplier Crz

4 结 论

当前，FLOW-3D 软件是唯一一个可以同时考虑大尺度界面掺气和气泡空间尺度分布的软件，值得在掺气水流的模拟中进行推广。然而，软件官方文档未对气泡尺度模型的细节进行详细说明，这不仅限制了对模型误差的分析，也限制了软件的普及应用。本文通过数值试验对相关模型的黑匣子细节进行了逆向探究，同时对关键模型参数进行了敏感性分析。研究表明：对于明渠自掺气水流，气泡大小主要受临界毛细管数控制，而临界韦伯数仅在掺气水面附近对模拟有微弱影响。在本文测试的参数中，拖曳系数和Richardson-Zaki 调节系数对计算结果的影响最为显著，主要体现在掺气浓度分布和水体上部的气泡半径上。总体来看，大于默认值的拖曳系数和Richardson-Zaki 调节系数会提高湍流强度并增加掺气，且小于默认值的参数对计算结果的影响更为显著。临界毛细管数、临界韦伯数及气泡初始直径等参数对计算结果的影响很小。在不同算例的模型调校中，应主要对拖曳系数和Richardson-Zaki 调节系数进行调校，以提高模型计算的准确性。