基于目标一致算法的导弹编队控制与仿真

许山山， 史涯晴， 韩敬利， 简开宇

(陆军工程大学 指挥控制工程学院，江苏 南京 210007)

随着信息技术的发展和各国反导防御系统的演进，单枚导弹的突防效率已经远远不满足理想的作战效能，如何提高导弹的突防性能是亟须解决的一个重要问题。导弹编队协同作战是采用密集临空饱和攻击的方式间接实现导弹突防能力的提升，为了达到这一目的，需要应用导弹编队飞行控制技术实现导弹的集群化和协同化。导弹编队飞行控制是在导弹飞向特定目标或方向的过程中，保持导弹之间预定的几何形状(编队)，同时适应环境约束(例如避开障碍物)[1]。现有的集群飞行控制研究主要集中在各种无人机或机器人的集群控制方面，与之对应的一些技术在军事和民用领域都得到了很好的验证与应用。考虑到导弹编队飞行控制与无人机群编队控制在轨迹、姿态控制、动力学方面具有相似性，所以利用无人机群相关理论和控制算法解决导弹编队队形和控制是可行的，很大程度上可以提高集群导弹的整体作战效能，尤其是在导弹的突防方面。

集群导弹编队飞行是由多枚导弹组成，采用一定结构编队攻击特定目标的作战方式，可确保导弹与导弹之间在飞行过程中保持一定的恒定距离[2]。编队控制方法大多集中于解决集群导弹系统的几何问题，采用的方法主要有领弹-从弹法、虚拟结构法、基于行为法等[3]。基于虚拟结构编队控制方式最主要的缺点是外部环境需要具有较高的计算能力和较强的通信能力；而基于行为法的缺点是无法进行系统的稳定性分析。但是采取领弹-从弹法，不仅可以降低计算机处理数据的能力，而且控制效果较好。目前国内外对编队控制器的研究主要集中在航天器和无人机飞行方面[2，4]，对导弹方面的研究还比较少。刘高旗等[5]将无人机队形重构的连续时间最优控制问题离散化为非线性规划问题进行求解，但是对计算性能要求较高[5]。基于以上方法的优缺点，本文采用基于目标一致算法[6]研究集群导弹系统的编队协同控制问题，其具有查找合适控制器的简单性和集群导弹系统网络结构的灵活性。首先，对导弹编队控制系统[7]进行建模，提出系统的编队控制算法；其次，在控制律中应用一种领弹-从弹结构，使领弹可以向从弹提供其期望状态等命令以降低计算机对数据的处理能力，如图1所示。在满足多导弹组成的网络基本假设的情况下，所提出的控制算法能精确地保持编队。最后，根据模型在MATLAB中进行仿真实验，验证了算法的有效性。

图1 导弹编队控制系统

1 集群导弹系统描述

下面介绍将导弹建模为四阶系统[6]，利用图论建模集群导弹之间信息传递的网络结构，并定义控制目标。

1.1 导弹建模

假设存在运动特性相同的导弹，每个导弹具有4个喷管和1个控制器，每个喷管可以单独从控制器获取命令。为简化模型，做如下假设：首先，导弹忽略外部空气动力；其次，喷管对命令响应足够快，可以忽略从控制器给喷管命令到喷管实际产生改变的时间延迟；再次，导弹飞行的高度不变，并且不发生偏航；最后，控制器不给导弹偏航力矩命令。在此假设下，给出导弹纵向和横向的线性化模型。

(1)

式中：x和y分别为导弹在x轴、y轴的位置；u和v分别为导弹在x轴、y轴的速度(m/s)；φ和θ分别为横摇姿态角、俯仰姿态角(rad)；p和q分别为横摇角速度、俯仰角速度(rad/s)；Mφ和Mθ分别为横摇控制力矩、俯仰控制力矩(N·m)；Ixx和Iyy分别为横摇惯性矩、俯仰惯性矩(kg·m2)；g为引力常量(m/s2)。

导弹平衡点是导弹在飞行高度和飞行速度不变的状态。

定义新的导弹状态变量为

(2)

(3)

利用式(1)～式(3)将新的导弹状态空间运动方程写为

(4)

继续定义新的导弹状态变量为

(5)

(6)

上标表示变量的顺序。利用式(4)～式(6)将新的导弹状态空间运动方程写为

(7)

结合具有相同顺序的纵向变量和横向变量，定义新的状态变量为

(8)

(9)

式中：下标i为导弹i。

利用式(7)～式(9)得到以下导弹模型四阶系统:

(10)

1.2 面向用户的网络结构建模

将导弹系统模型创建为一组信息交互的动力系统，利用图论描述集群导弹组成的信息网络[6]。

利用图G=(V,A)建模导弹之间的信息交互，其中V={v1,v2,…，vN}是一组节点，A∈V×V是一组边。图G中的边(vi,vj)为一条从导弹i到导弹j的网络路径，表示导弹j可以从导弹i中获取信息。

设A∈RN×N，D∈RN×N和L∈RN×N分别是与图G相关的邻接矩阵、度矩阵和图拉普拉斯矩阵。邻接矩阵A=[aij]的分量归纳为

(11)

如果导弹j通过网络从导弹i获取信息，aij设置为1，否则aij设置为0。

度矩阵是一个入度矩阵，定义为

D=diag[deg(v1),deg(v2),…,deg(vN)]

(12)

式中：deg(vi)为到达节点的通信链接数量。

图拉普拉斯矩阵为

L=D-A

(13)

1.3 控制目标

从弹和领弹编队飞行的理想状态如图2所示[6]，图2中显示了3个从弹跟随领弹列队飞行。

为实现从弹跟随领弹的飞行任务，将控制目标[6]定义为：每个从弹跟随领弹，并且从弹位置渐近收敛到从弹和领弹之间的一个期望相对位置，可表示为

图2 理想编队队形

(14)

式中：ri为从弹i的位置；rL为领弹的位置；di为从弹i与领弹之间的期望相对位置。相关符号定义如图3所示。需要注意的是，从弹的期望相对位置i与任何其他从弹位置不同。

图3 相关符号定义

为实现控制目标，做如下假设。

假设1：每个从弹必须通过网络上的领弹进行连接，但并非所有从弹都必须通过领弹进行直接连接。此外，每一对不同的从弹之间必须有一个交互式通信链路。

假设2：领弹的运动必须独立于任何导弹，即领弹的运动不受任何导弹的影响。

2 队形控制器设计

笔者提出一种基于目标一致算法来实现1.3节中的控制目标。

2.1 基本思路

编队控制主要是控制率设计，使导弹编队中的从弹能够到达期望位置，跟随领弹遂行完成作战任务，采用的控制结构[3]如图4所示。

图4 编队控制框图

基于目标一致算法的主要功能步骤如下。

① 确定作战任务目标，算法将此目标认定为所有单一智能体的共同目标。

② 根据领弹参考轨迹确定从弹飞行轨迹，通过计算获得从弹距离领弹的期望位置。

③ 领弹在计算处理完数据后，将信息传递给连接的从弹，从弹实现轨迹修正，将修正信息反馈给领弹。

④ 算法将反馈信息数据进行处理后，正向传递给从弹进行验证并且继续修正飞行轨迹。

2.2 编队控制律设计

为实现控制目标，分别考虑一组导弹的共同目标和每个导弹的单独目标，前者采用基于目标一致的合作控制算法实现共同目标，后者采用领弹-从弹结构实现单独目标。领弹提供位置给与自己直接连接的从弹并将理想的位置作为命令传递给从弹。该控制算法的优点是所有从弹不必直接与领弹连接，满足假设1和假设2的最小网络结构就足以实现控制目标。

适用于导弹飞行器的控制律[6]为

(15)

(16)

(17)

式中：Mi(t)为控制力矩;αij为导弹j是否从导弹i获取信息;βk为控制增益。

设由N个(≥1)从弹(表示为式(10))和一个领弹组成的集群导弹系统满足假设1和假设2。设由从弹和领弹组成的网络的图拉普拉斯算子的非零最小特征值为λmin。将控制律式(15)应用于每个导弹，当控制器增益为βk时，对k∈{0,1,2,3}，使其满足以下一个条件，则渐近达到控制目标(式(14))。

βk>0, ∀k∈{0,1,2,3}

(18)

(19)

β1β2>β0β3

(20)

3 编队仿真模型

滚动、俯仰和速度是影响导弹飞行过程中的重要参数，通过仿真实验修改相关参数并分析结果，验证算法的有效性。需要说明的是，本文主要以导弹为研究背景，采用的仿真实验算法均来自开源项目，得到的实验数据均是模拟数据，与实际导弹参数无直接关联，研究的意义在于为导弹编队提供技术参考。

3.1 仿真设置

考虑一个单一的网络，且在每一对不同的从弹之间有交互通信链路，如图5所示。其主要特点是只有中继从弹直接从领弹获取信息，其他从弹间接从领弹获取信息。该网络的图拉普拉斯算子的非零最小特征值为λmin= 0.2。

图5 通信网络示意图

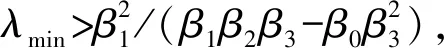
假设一组导弹编队分别由4个从弹和1个领弹组成，控制器β=[β0，β1，β2，β3],设置两组实验分别调整β1、β2，每组实验设定4个仿真方案，具体如表1所示。

表1 两组实验的数值模拟条件

3.2 仿真结果

3.2.1 调整β2实现对导弹方向(滚动、俯仰)的控制

按照方案一设定参数进行60 s仿真，模拟领弹(红色)和从弹的运动轨迹并得出结果，如图6所示。方案二、方案三和方案四的仿真结果分别如图7、图8和图9所示。

① 使用默认值，得到所需的行为(与一些可能的路径冲突)如图6所示，频繁的滚动和倾斜的系统将会导致更高的碰撞概率。

② 减小β2值，仍然满足方程中给定的约束条件，但使收敛速度更快，转弯更快(避免了与领弹的路径冲突)。

③ 模拟最小约束条件下的β2=3，导致导弹的飞行轨迹会发生振荡，一定时间内会趋于稳定，但是如果β2进一步变小，会导致轨迹不稳定。

④ 如果β2进一步变小，会导致轨迹不稳定。

3.2.2 调整β1实现对导弹速度的控制

① 当β1=0，破坏最小约束，导致从弹绕着领弹飞行的半径越来越大，一旦领弹飞行停止，编队永远不会聚合，如图10所示。

② 当β1≤4时，跟随领弹飞行的从弹移动速度加快，穿越特定距离前会出现减速，这样领弹就可以赶上从弹，从而导致导弹运动轨迹出现振荡，也同时增加了收敛时间，如图11所示。

③ 当4≤β1≤17时，从弹可以正常跟随领弹编队飞行，如图12所示。

④ 当β1>17时，从弹不会跟随领弹编队飞行，从实验结果来看，超出这个范围都会造成轨迹的不稳定或者不聚合，如图13所示。

图6 方案一：β=[1,5,15,3]

图7 方案二：β=[1,5,7.5,3]

图8 方案三：β= [1,5,3,3]

图9 方案四：β=[1,5,1.5,3]

图10 方案一：β1=0，β=[1,β1,15,3]

图11 方案二：β1<4，β=[1,1,15,3]

图12 方案三：4<β1≤17，β=[1,β1,15,3]

图13 方案四：β1>17，β=[1,β1,15,3]

3.3 小结

实验1结果表明，随着β2的减小，导弹编队模拟结果趋于发散，其值越大，导弹编队状态越稳定。这表明通过合理调整控制器增益参数β2，能够实现控制导弹编队的稳定性。实验2结果表明，当β1时处于[4,17]这个区间时，从弹可以正常跟随领弹编队飞行，这表明通过合理调整控制器增益参数β1，也能够实现控制导弹编队的稳定性。

4 结束语

为实现导弹编队控制，提高导弹编队协同作战的稳定性，实现密集临空饱和攻击，从而提升导弹突防作战效能，本文将导弹的线性化模型表示为四阶系统，利用图论方法对编队导弹之间的信息网络结构进行建模，提出了四阶系统的编队控制算法。针对一阶不考虑动力学特性的编队控制问题，直接将编队控制算法推广到四阶不考虑动力学特性的编队控制系统，并采用了领弹-从弹结构，使领弹可以为从弹提供编队的几何配置指令。由领弹和从弹组成的编队必须满足一个从弹直接获取领弹指令，以及每一对不同从弹之间具有交互式通信链路的要求。编队控制算法通过确定控制器的增益以实现控制目标。根据相关假设和要求进行仿真实验，结果表明，该算法对于具有四阶动力学的导弹编队飞行是有效的。