基于光学扫描的高精度基准孔测量方法研究

陈 强， 陈代鑫， 雷 沛,2， 孙海龙,2， 代玉淋,2

(1.成都飞机工业(集团)有限责任公司，四川 成都 610092；2.四川省航空智能制造装备工程技术研究中心，四川 成都 610092)

随着飞机设计和制造的不断发展，以及飞机装配对效率、质量和精度要求的不断提升，自动钻铆系统在国内外航空制造企业中得到了广泛的研究和应用[1-6]。美国GE公司和EI公司、德国宝捷公司等都已经研发出了比较成熟的系统。在国内，一些高校、科研院所和企业对自动钻铆技术也做了深入研究，研制了自动钻铆系统。随着自动钻铆系统的广泛应用，提高自动钻铆的精度和质量成为了当前研究的热点方向。飞机装配中铆钉孔的位置精度直接影响飞机的装配质量和使用寿命，因此提升铆钉孔位置精度具有十分重要的意义。

由于飞机零件加工误差和装配误差的存在，导致飞机部件实际制孔位置与理论制孔位置存在一定的偏差。如果直接按照理论制孔位置对飞机部件进行制孔可能造成制孔位置超差，从而导致产品报废。为了避免这种情况发生，在实际应用中通过在产品表面设置基准孔，利用基准孔位置对理论制孔位置进行纠偏，从而保证实际制孔位置精度满足产品装配±0.5 mm的精度要求。因此，保证基准孔位置的识别精度，对提高产品制孔位置精度具有决定性作用。国内外学者对基准识别进行了大量的研究，其中最主要的方法有单目视觉测量法和双目视觉测量法。单目视觉测量只能计算出基准孔平面二维坐标[7-10]，在飞机翼面类部件装配中应用广泛。但在大曲率飞机部件装配的应用中，单目视觉测量需通过第三轴理论数据进行组合才能得到基准孔的三维坐标，由于此方法采用了部分理论数据导致测量精度不高，存在许多的弊端。双目视觉测量通过两个相机同时对基准孔进行测量，标定计算后得到基准孔的三维坐标，此方法的测量精度较高[11-12]，但是双目视觉测量需要2个工业相机导致测量装置体积较大，在自动钻铆系统中安装比较困难。

为此，本文提出了一种基于线激光扫描的基准找正方法，利用一个线激光扫描仪和一个伺服电机组成基准扫描装置，对基准孔进行扫描测量，得到产品表面点云数据，最后通过边界识别和椭圆拟合计算得到基准孔圆心三维坐标。该方法主要优势在于激光线扫描装置结构紧凑、安装便利，可以与自动钻铆系统有效地结合；利用标准平面可实现激光线扫描装置的快速标定，大幅提高了标定效率；激光线扫描装置可直接实现基准孔圆心三维坐标测量，对实现大曲率飞机部件基准孔的精确测量以及提升制孔位置精度具有重要意义。

1 光学扫描仪标定

数字化钻铆系统采用五轴数控机床作为运动单元，其示意图如图1所示，包含X轴、Y轴、Z轴、A摆、B摆。线激光扫描基准找正原理如图2所示。线激光扫描仪与伺服电机相连，伺服电机带动线激光扫描仪对基准孔进行扫描。

建立与机床制孔末端执行器固连的坐标系O′-xyz，其中坐标原点与机床RTCP重合，当机床旋转轴A、B旋转角度均为0时，该坐标系3个轴的方向与机床坐标系O-xyz的3个轴的方向平行。

建立与机床制孔末端执行器固连的坐标系O″-xyz，当滑台在原点时，坐标原点与线激光扫描仪测量原点重合，X轴和Z轴分别与线激光扫描仪光线测量坐标系X轴、Y轴平行。

图1 五轴加工机床示意图

图2 线激光扫描基准找正原理

(1)

假定基准平面在坐标系O′-xyz下的方程为

ax+by+cz=d

(2)

假定坐标系O″-xyz与坐标系O′-xyz之间的旋转关系为

(3)

其中，R中元素满足以下关系。

(4)

因此，可以得到测量点在坐标系O′-xyz下的坐标为

p′=p0+R·p″

(5)

式中：

(6)

将式(3)、式(5)和式(6)代入式(2)，得到式(7)。令式(7)中Δy=0，可以得到式(8)。由9个相互不平行的基准面可以得到式(9)。

a·(x0+A1·(x+μ·Δy)+A2·v·Δy+A3·(z+ω·Δy))+b·

(y0+B1·(x+μ·Δy)+B2·v·Δy+B3+(z+ω·Δy))+

c·(z0+C1·(x+μ·Δy)+C2·v·Δy+C3·(z+ω·Δy))=d

(7)

a·(x0+A1·x+A3·z)+b·(y0+B1·x+B3·z)+
c·(z0+C1·x+C3·z)=d

(8)

ai·(x0+A1·x+A3·z)+bi·(y0+B1·x+B3·z)+
ci·(z0+C1·x+C3·z)=di,i=1,…,9

(9)

将式(9)改写为矩阵形式：

A1X1=D1

(10)

其中A1、X1、D1分别如式(11)、(12)、(13)所示。

(11)

(12)

(13)

利用矩阵运算可得：

(14)

利用式(4)可以求解得A2、B2和C2。

令式(7)中x=0，可得：

a·(x0+A1·μ·Δy+A2·v·Δy+A3·(z+ω·Δy))+
b·(y0+B1·μ·Δy+B2·v·Δy+B3·(z+ω·Δy))+
c·(z0+C1·μ·Δy+C2·v·Δy+C3·(z+ω·Δy))=d

(15)

由3个相互不平行的基准面可得：

(ai·A1+bi·B1+ci·C1)·Δyi·μ+(ai·A2+bi·B2+ci·C2)·Δyi·
v+(ai·A2+bi·B2+ci·C2)·Δyi·ω=di,i=1,…,3

(16)

将式(16)改写成矩阵形式为

A2X2=D2

(17)

式中：A2、X2、D2分别如式(18)～式(20)所示。

(18)

(19)

(20)

利用矩阵运算，可以求得：

(21)

坐标系O′-xyz与机床坐标系O-xyz之间的关系为

R(α,β)=Rx(α)Rz(β)

(22)

式中：α为机床A摆角度；β为机床B摆角度。

(23)

(24)

机床RTCP点在机床坐标系O-xyz下的坐标为

(25)

因此，可以得到测量点在机床坐标系O-xyz下的坐标为

PS=P+R(α,β)·p′

(26)

2 基准孔识别

利用线激光扫描仪对基准孔进行扫描，通过式(1)可以计算得到基准孔及附近曲面在坐标系O″-xyz下的点云坐标集为

P″={p″(i)},i=1,…,n

(27)

当滑台移动距离Δy为定值时，线激光扫描仪测量得到的点云集如图3所示。定义点云集相邻两点之间z轴坐标值变化量为Δz，X轴坐标值变化量为Δx,其中Δx为定值。由于飞机表面的光顺性，设定飞机表面任意相距Δx两点之间Δz的最大值为ε。

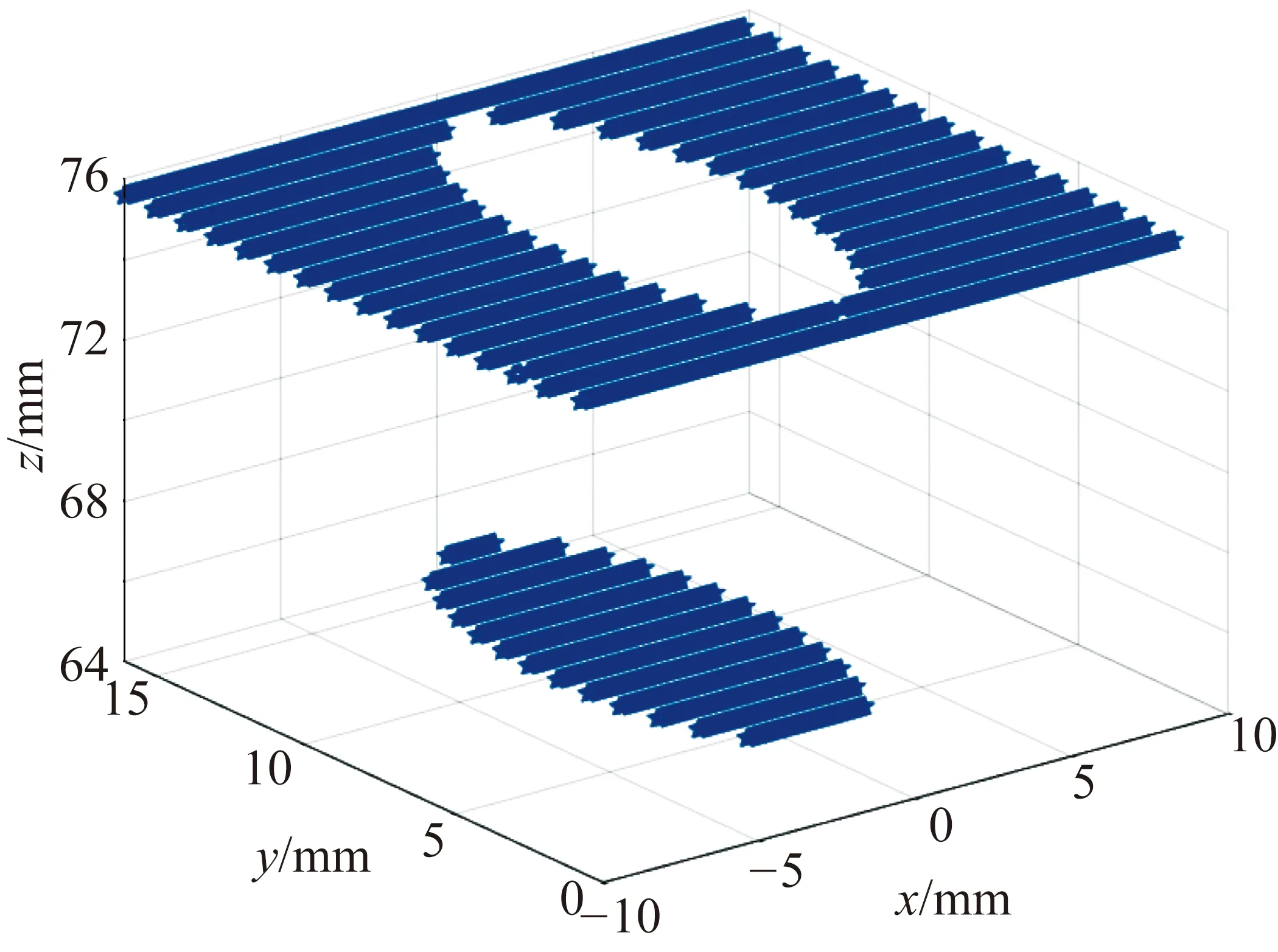
图3 基准孔点云集

建立目标函数为

(28)

(29)

图4 边界提取原理

图5 边界点平面图

平面椭圆一般方程为

x2+Axy+By2+Cx+Dy+E=0

(30)

利用式(30)可以求解出基准孔圆心的x、y坐标为

(31)

(32)

利用最小二乘法对椭圆进行拟合，使式(32)取值最小，则有：

(33)

由式(33)可以得到正定方程组为

TC=K

(34)

其中：

(35)

(36)

(37)

利用矩阵运算可以求得椭圆方程系数为

C=(TTT)-1TTK

(38)

利用式(31)可以计算出椭圆圆心坐标。

(39)

3 实验验证

实验采用图6所示的五轴加工机床，其技术参数如表1所示。钻铆末端执行器包含制孔和抽铆功能，如图7所示。线激光扫描仪采用的是某公司生产的二维扫描传感器，其参数如表2所示。

表1 机床技术参数

图6 五轴加工机床

图7 钻铆末端执行器

表2 线激光扫描仪参数

利用机床末端执行器上的扫描仪对测量孔进行测量并针对不同扫描步长进行了测试，最终与激光跟踪仪(型号Leica AT960，测量精度±0.01 mm)测量的数据进行对比，实验结果如表3所示。

表3 实验结果

其中测量孔直径为10 mm，精度为H9。扫描仪距离测量孔距离范围为90～110 mm。扫描仪X轴长度分辨率计算公式为

(40)

根据式(40)，可以得到在验证条件下，X轴分辨率为0.0378125～0.0428125 mm。

从表3中数据可以看出，当扫描步长在0.1～1 mm之间变化时，扫描测试结果始终保持一致，且与激光跟踪仪的测量结果误差始终保持在±0.1 mm之内。当扫描步长增大至2 mm时，测量结果与激光跟踪仪结果误差在0.2 mm。但扫描步长增大至3 mm以上时，误差达到了1 mm。造成此现象的主要原因为当扫描步长增大至3 mm以上时，直径为10 mm的测量孔扫描得到的包含孔边界的数据量变小，从而导致拟合精度降低。

从表1可看，机床的定位精度优于±0.1 mm。因此，针对直径为10 mm的基准孔，扫描步长在2 mm以下时，通过该方法进行基准识别，可以使制孔位置精度满足飞机装配±0.5 mm的精度要求。

4 结束语

本文提出了一种适用于数字化钻铆系统的高精度基准找正技术。首先，采用一个线激光扫描仪和伺服电机组成集成基准扫描装置，机械地对基准孔和附近特征进行扫描，得到测量点数据集；然后，利用基准孔特性对测量点数据进行边界提取，并采用最小二乘法进行椭圆拟合计算，得到基准孔圆心坐标；最后，利用标定出的基准找正装置坐标系与机床坐标系的转换关系计算得到基准孔在机床坐标系下的位置。实验证明该方法能够用于数字化钻铆系统的基准找正，满足飞机装配精度要求。同时，该方法可以针对不同应用场景和精度要求调节激光线扫描仪的扫描步长，从而控制基准孔识别精度。相对于单目视觉测量，该方法可以实现基准孔三维坐标的准确测量；相对于双目视觉测量，该方法使用的测量装置体积较小，便于安装和布置；相对于利用激光跟踪仪进行测量，该方法在整个测量和计算过程中不需要人工介入，系统自动化程度更高，整个测量速度更快。