基于缩聚理论的主轴箱刚度表征方法
高羡明,华梦怡,张功学,李端玲,郭宁波
(陕西科技大学机电工程学院,陕西西安 710021)
0 前言
加工精度是衡量机床加工能力的主要技术指标,直接决定着被加工工件的质量[1-3]。切削载荷和机床刚度是影响加工精度的两个重要因素[4-6]。其中切削载荷受刀具材料、工件材料等外部因素影响;机床刚度受机床拓扑布局方案或结构构型等内部因素影响,这类内部因素也是机床设计制造过程中调整成本较高的部分。因此,机床刚度信息对提升机床加工精度有重要意义。
目前,获取机床刚度信息的方法主要有检测法与仿真法两种[7-9]。检测法是对机床部件刚度直接进行测量[10-11],如镗铣床位置刚度检测、车削中心刚度检测等[12-15]。但检测法仅针对离散点的位置刚度进行了测量[16],无法全面评价机床在连续范围内的刚度情况。仿真法是通过有限元分析方法建立机床的有限元模型[17-18],这种方法虽然能够在连续范围内反映刚度的分布情况,但对于机床这类复杂装备,其有限元模型的规模会随着结构的复杂程度增大,从而使运算量急剧增加。此外,当机床受载情况发生改变时,又需要对有限元模型重新进行分析求解,耗费大量运算时间,应用范围被极大地限制。随着数字孪生技术的发展,目前急需一种能够快速计算、实时表征机床刚度特性的方法。
在刚度建模领域,部分学者提出了一种刚度缩聚理论。GUYAN[19]在静态结构刚度矩阵和质量矩阵的缩聚研究中,将结构中不受外载作用的节点视为内部节点,对结构的刚度矩阵和质量矩阵进行了推导简化,获得了一种基于有限元技术的刚度矩阵缩聚方法。由于机床属于大型复杂装备,其刚度矩阵的规模及有限元分析的运算量巨大,因此刚度缩聚理论存在应用于机床刚度分析领域的可能性。
基于以上机床刚度分析的研究背景和现状,本文作者将刚度缩聚理论引入机床的刚度分析中,并将其与有限元技术相融合,提出一种通用于机床的刚度特性归一化表征方法。再以THM46100型卧式加工中心的主轴箱系统为例,运用此方法建立该主轴箱的刚度表征模型,再对比验证镗削工况实际载荷下该模型和有限元分析法求解所得的主轴箱变形量结果,表明采用此方法建立的刚度表征模型能够在保留刚度特性的同时,大大降低运算量,提高分析效率,能够满足数字孪生技术发展下、机床等复杂装备领域中,实时动态反映刚度数值变化、快速解算空间刚度场的需求。
1 分析方法
1.1 刚度缩聚理论
刚度缩聚是一种根据约束和载荷条件对系统的刚度矩阵进行缩聚简化的过程。基于此思想作如下推导:
在结构分析中,系统的结构方程可表示为
F=Kx
(1)
式中:F为载荷矩阵;K为刚度矩阵;x为位移矩阵。
又可将式按各组成模块细分为
(2)
因为系统中存在着不受外部作用力的组成模块,即存在着F2=0,则式(2)与下式等价:
(3)
由此可知,系统在实际受载情况下的刚度矩阵可简化为
(4)
由以上推导可以看出,在特定载荷和约束条件下对系统的刚度矩阵进行缩聚,原始刚度矩阵中的所有元素对缩聚后的刚度矩阵均有贡献,证明了刚度缩聚可在完整保留系统刚度特性的情况下减少矩阵的阶数,便于提高后期矩阵运算的效率。
1.2 基于刚度缩聚理论的刚度表征方法
如图1所示,基于刚度缩聚理论的刚度表征方法的大体思路是:将表征对象划分为多个子系统模块,分析各模块间的载荷传递关系,辨识出表征对象的关键几何特征;应用刚度缩聚理论消除未受外载作用的子系统坐标,运用有限元分析方法提取关键几何特征的变形量,以矩阵形式建立表征对象的刚度模型,反映其刚度与所受载荷间的关系;在同一工况载荷条件下,分别采用已建立的刚度表征模型和有限元分析法求解系统变形量,对比分析求解结果,验证模型建立的准确性;逐一分析模型矩阵中各元素的数值信息,识别出刚度薄弱方向,从而进行加工精度预测,明确结构设计的优化目标。

图1 基于刚度缩聚理论的刚度表征方法研究思路Fig.1 Research ideas on the stiffness characterization method based on stiffness polycondensation theory
对表征对象进行刚度缩聚时,应先确定表征对象各组成模块间的载荷传递关系,识别受外部载荷作用的关键几何特征。将表征对象系统按照几何结构关系进行分类,能够得到不同的子系统模块,每个子系统模块的承载端同另一个子系统模块的约束端首尾相连,这样系统即被等效成为一个串联弹簧系统模型。对此模型的载荷传递路径进行分析,可以发现外部载荷总是自系统的承载端节点向约束端节点传递,各模块间的变形传递也是一维线性叠加的关系。因此,系统中受外部载荷作用的关键几何特征一般即为系统的承载端和约束端。
在辨识出系统的关键几何特征后,应结合有限元技术求解关键几何特征的变形量。在有限元仿真平台中建立系统的有限元模型,对系统的约束端施加固定约束条件,对承载端分别施加x、y、z、a、b、c六向的单位力与单位力矩,求解其相应变形量,再结合其空间位置关系对求解结果进行提取处理,按照式(5)所示的柔度矩阵反映系统变形量与承载端载荷之间的关系。
(5)
式中:R为表征系统变形量与所受载荷间关系的柔度矩阵;δij为作用在j方向的力fj(j=x,y或z)或力矩Mj(j=a,b或c)引起的系统承载端i(i=x,y或z)方向的位移变形量;θij为作用在j方向的力fj(j=x,y或z)或力矩Mj(j=a,b或c)引起的系统承载端i(i=a,b或c)方向的转角变形量。
此外,柔度矩阵中各元素数值的大小还直观地表现了系统刚度特性的薄弱环节。该矩阵前3行元素数值信息分别反映x、y、z方向上的抗弯刚度,其中,左上3×3区域元素单位为μm/kN,右上3×3区域元素单位为μm/(kN·m);后3行元素数值信息分别反映a、b、c方向上的抗扭刚度,其中,左下3×3区域元素单位为10-3rad/kN,右下3×3区域元素单位为10-3rad/(kN·m)。
因此,可建立表征对象的刚度表征模型如式(6)所示,对于任意载荷作用下的系统总变形量均可通过该式进行求解。
δ6×6=K6×1F1×6
(6)
式中:K为表征系统变形量与所受载荷间关系的刚度矩阵,K=R-1。
2 机床主轴箱的刚度表征实例应用
为进一步说明此方法的应用,以某机床企业生产的THM46100精密卧式加工中心的主轴箱为研究对象进行实例分析。可将该主轴箱系统按照其组成关系进行分类,得到3个子系统模块,分别为主轴、箱体和滑块子系统模块。
2.1 主轴箱有限元模型的建立
建立THM46100精密卧式加工中心主轴箱系统的有限元模型。在保证有限元分析精度的条件下,对其结构进行适当简化,忽略一些对主轴箱系统刚度特性影响很小或无影响的细微结构(例如螺纹孔、小倒角、小凸台等),简化后的模型如图2所示,并在有限元平台中对其各子系统模块按照表1所示材料参数进行设置。

图2 THM46100精密卧式加工中心主轴箱有限元模型

表1 主轴箱系统有限元模型材料属性设置
2.2 主轴箱刚度表征模型的建立
为识别主轴箱系统的关键几何特征,对其载荷传递关系进行分析。主轴箱系统在机床加工时,外部载荷(切削载荷)总是自主轴与刀具接触的刀具装夹孔开始,沿着主轴→箱体→滑块的路径进行传递。因此,主轴箱系统的关键几何特征为承载端主轴接触面和约束端滑块安装面。
在有限元平台中对主轴箱有限元模型的约束端滑块安装面进行约束,对承载端主轴接触面分别施加x、y、z三个方向的单位力(fx、fy、fz)及A、B、C三个方向的单位力矩(Ma、Mb、Mc),分别求解主轴箱有限元模型在这六向载荷下的变形。在主轴前端装夹刀具处均布选取4点作为关键特征点,提取关键特征点的有限元计算结果并进行处理,获得其位移变形量及转角变形量如表2所示。
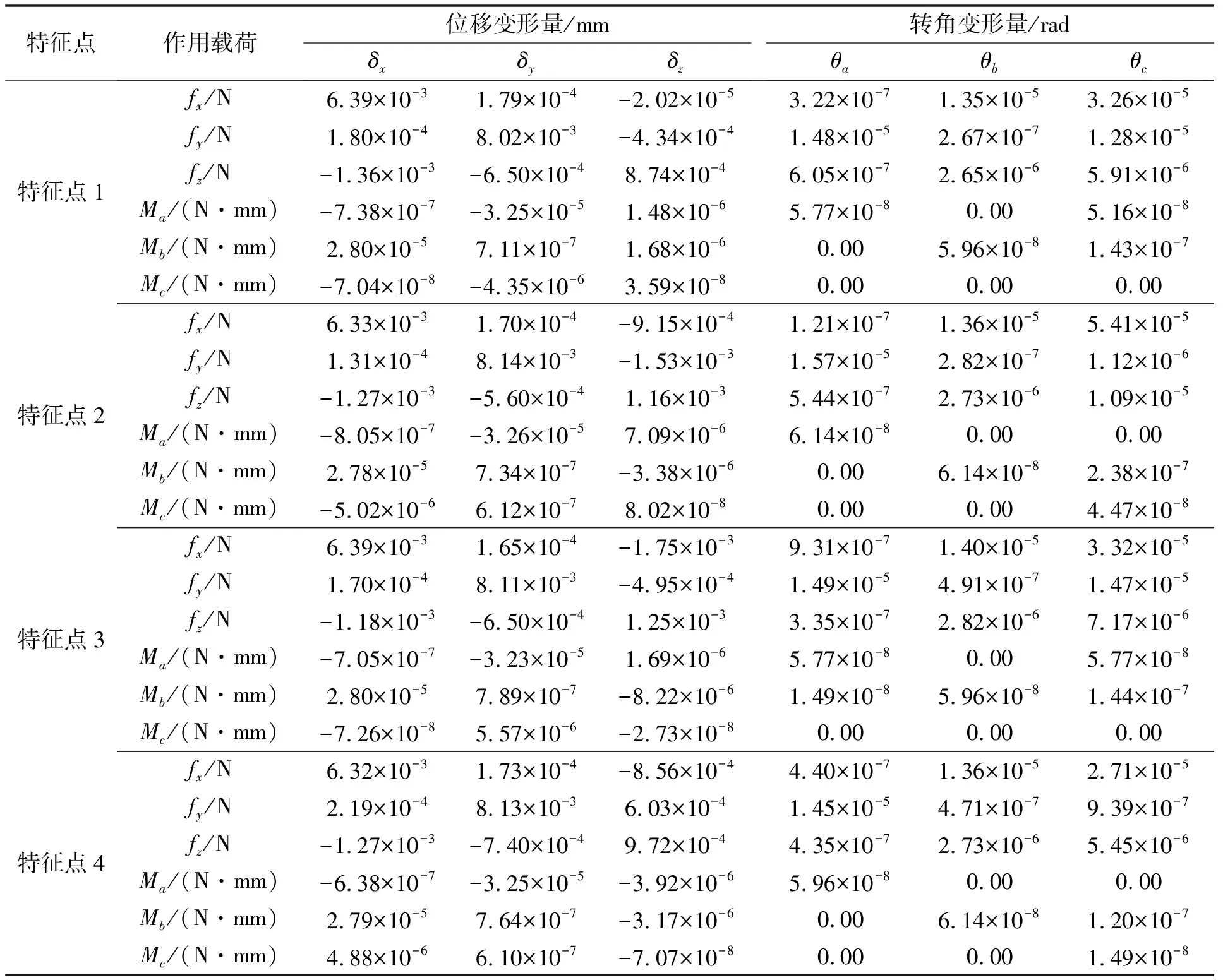
表2 主轴箱关键特征点在六向载荷下的位移、转角变形量
按照主轴箱关键特征点的空间位置关系,以及所述的刚度表征建模方法,对表2所获得的数据进行处理,建立主轴箱系统的刚度表征模型,如式(7)所示:
(7)
此模型也反映了主轴箱系统所受外部载荷与其相对于地面坐标系变形量之间的关系。
进一步观察已建立的刚度表征模型,对比矩阵元素的数值大小,可识别出主轴箱系统的刚度薄弱方向。如图3所示,在主轴箱系统柔度矩阵中,第一行第一列和第一行第五列、第二行第二列和第二行第四列的元素数值最大,分别表征了主轴箱系统在fx、Mb作用下x向的抗弯刚度和在fy、Ma作用下y向的抗弯刚度。由此可知,应将提高x、y两向的抗弯刚度作为主轴箱系统刚度优化设计目标。
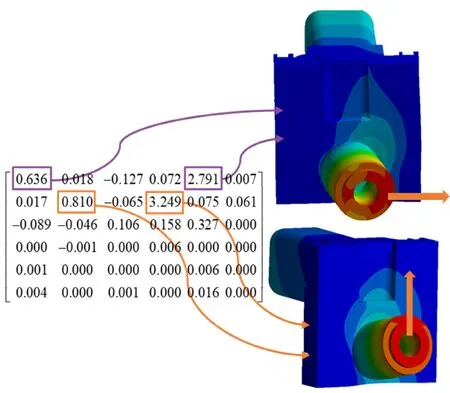
图3 主轴箱刚度表征模型识别刚度薄弱方向
3 主轴箱刚度表征模型的验证
为了验证上文建立的主轴箱系统刚度表征模型的准确性,分别利用有限元分析方法和刚度表征模型,对镗削加工时机床受力与变形的关系进行分析。如图4所示,机床在镗孔时所受的外部载荷主要为主切削力Fc、背向力Fp和进给力Ff。此时,主轴箱系统在这些外部载荷的影响下会受到一个作用力F和作用力矩M。当刀具材料选用45钢时,可由镗削指数型切削力经验公式[20]对其进行计算。
(8)
(9)
(10)
(11)
式中:ap为切削深度,mm;f为进给量,mm/r;v为切削速度,r/min;KFc、KFp、KFf为各种影响因素对3个切削分力影响的修正系数的乘积。

图4 机床镗削加工时的载荷分析Fig.4 Load analysis when machine tool boring and processing
因此,当机床镗削采用切削速度v=130 r/min、切削深度ap=3 mm、进给量f= 0.25 mm/r的工艺参数时,根据式(8)—式(11)可确定主轴箱所受的外部载荷如表3所示。

表3 机床镗削加工时主轴箱系统受载情况Tab.3 Headstock load when machine tool boring and processing
分别利用有限元分析方法和建立的刚度表征模型,对该载荷条件下主轴箱系统的变形量进行求解,结果如图5所示。

图5 两种方法求解结果对比
由此可以直观看出:两种方法求解得到的主轴箱变形量大体一致,但采用刚度表征模型求解较有限元法相比,运算时长由原先的63 min缩短为0.84 s。这证明:基于刚度缩聚理论建立的主轴箱系统刚度表征模型,能够在准确反映主轴箱所受载荷与其实际形变之间关系的同时,极大程度减少运算时长,且对于不同工况的加载条件,也可以通过刚度表征模型对变形量直接进行求解,无需再通过有限元方法重复大量运算,提高了分析效率。
4 结论
将刚度缩聚理论和有限元分析方法相结合,以THM46100型卧式加工中心的主轴箱系统为研究对象进行实例分析,建立了包含具体参数信息的主轴箱系统刚度表征模型。通过进一步分析该表征模型的元素数值,识别出主轴箱系统的刚度薄弱方向为x、y两向的抗弯刚度,初步确定了其刚度优化的设计目标。选取机床镗削加工的实际工况载荷,对比有限元分析方法和直接采用该刚度表征模型求解所得的主轴箱变形量,验证了文中所述的归一化刚度表征方法,在保证了求解精度的同时大大提高了求解效率(由63 min缩短为0.84 s),能够对机床等复杂构型装备的刚度特性进行准确表征,能够实现不同载荷条件下系统变形的快速求解,为今后连续解算复杂装备刚度场提供了理论模型与方法支撑。

