基于局部和全局特征的点云对应关系构建

唐溯菡，谢晓尧，刘 嵩

(贵州师范大学 贵州省信息与计算科学重点实验室，贵州 贵阳 550001)

0 引言

近年来，随着物体三维信息获取设备的发展，点云数据的获取成本降低。对于点云数据的处理，例如刚性或非刚性配准、语义分割、特征提取、点云补全等研究开始受到广泛的关注。构建点云对应关系，即原点云和目标点云之间的映射关系，是点云配准中非常关键的步骤，对应关系的精确度会影响后续的配准算法的结果以及算法效率。目前的对应关系的构建可以分为两种：构建点-点的对应关系以及构建区域-区域的对应关系。

1 相关工作

区域-区域的对应关系是指将原点云和目标点云按照一定的方式分割，得到各个不同的部位后，在各个部位之间构建的对应关系，如图1所示。

图1 区域对应 Fig.1 Area Correspondence

点-点之间的对应关系即原点云和目标点云的点的映射关系。一些算法使用最近点搜索算法获取初始对应关系，然后对原点云使用非刚性配准算法，在其逐渐变形逼近目标点云的过程中动态更新对应关系。Brian等[1]提出一种基于最近点迭代(Iterative closest point，ICP)的非刚性配准算法，使用最近点搜索算法获取初始对应关系后，在原点云非刚性配准目标点云的过程中逐步更新对应关系。但这类方法只适用于形变程度不大、原点云和目标点云的实际上严格对齐的数据，如图2所示，且对应关系必须在非刚性配准的过程中重新计算，计算效率低。

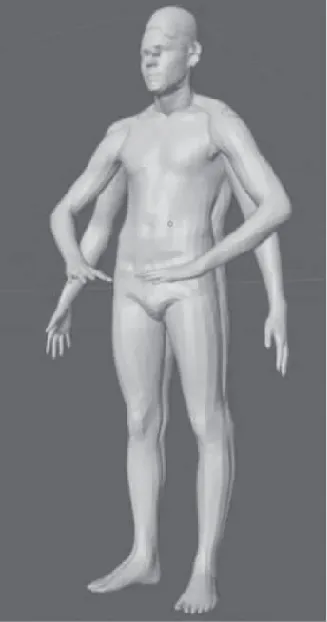
图2 模型的初始空间位置Fig.2 Initial position of the models

另一种算法的大体思路则是通过构建点云每个点的特征描述符后，根据设置的规则计算各个点之间的相似度，来进行匹配，得到初始的对应关系，后续对这些关系进行筛选和优化。 Cao等[2]使用了一种基于概率的方法计算对应关系，首先对原点云和目标点云进行降采样，然后使用相干点漂移配准(Coherent point drift,CPD)算法计算初始对应关系，并将两点间距离大于设定阈值的对应关系删除，最后使用基于自旋图像的方法再进行进一步筛选，得到相对可靠的对应关系集合。但是该方法适用于原点云和目标点云存在正确的部位重合，如图2所示，模型的躯干、头部和大腿部位是较准确的重合在一起的。Guo等[3]使用基于点云FPFH特征的方法计算出初始对应关系，原点云和目标点云在未发生形变或形变较小的部分由于相似度更高，因此更容易在这个部分得到更多的对应关系，基于这个逻辑，使用随机抽样(Random sample consensus，RANSAC)算法进行初始刚性配准，从而找到两个点云的重合部位(即形变较小的部分)，同时分离出不重合的部位(即发生大尺度形变的部分)，并对初始对应关系进行筛选。最后对原点云出现大尺度形变的部位与形变较小的部分的位置判断，构建原点云和目标点云的大尺度形变部位之间的对应关系。Sahillioglu等[4]通过积分测地线距离函数计算点云的局部极值来选取特征点并构建初始的稀疏对应关系，然后通过测地线距离计算每个对应关系的等距失真值构建一个投票矩阵，得到每个对应关系的权值，接着保留权值在设定阈值内的对应关系。然后重复特征点选取的过程，并利用稀疏对应关系拓展出新的对应关系。Sahillioglu等[5]则是通过测地线距离来对点云进行采样，并利用采样点进行对应关系计算。这个过程是迭代的，首先测地线距离一开始会设置较大，得到数量极少的原点云和目标点云的采样点点集，接着在两个采样点集之间进行两两对应关系的构建，并通过测地线距离计算等距失真值，来进行对应关系的筛选，然后降低测地线距离，重复以上步骤，直至达到人工设置的计算次数或者点云中的每个点已经拥有对应关系，与第一步不同的在于，之后构建对应关系时，一些点的近邻点已经拥有对应关系，那么这些点的计算对象会被压缩到一定的区域，从而降低计算时间。Tam等[6]提出了一种基于谱裁剪算法对对应关系进行筛选和优化的方法，在用一些方法得到初始对应关系后，对每一对对应关系，利用其近邻点以及近邻点的对应关系，基于测地线距离构建出一个局部的框架图，在此基础上使用扩散框架计算每个对应关系的置信度，从而对每个对应关系进行筛选。 李俊[7]基于滑动分析提取出点云特征点后，根据多尺度下的局部曲率构建特征点的特征描述符，利用特征描述符的欧式距离构建初始的稀疏对应关系，基于测地线距离，使用RANSAC-谱裁剪算法剔除稀疏对应关系中的错误匹配，接着利用得到的稀疏对应关系进行粗刚性配准，最后使用最近点搜索得到每个点的对应关系。田利利[8]使用超体素分割算法(Voxel cloud connectivity segmentation,VCCS)对点云进行降采样操作后，使用热核特征构建每个点的特征描述符，使用欧氏距离构建初始对应关系，然后使用联合一致分割算法[9]，将两个点云分割出多个一致的对应区域，并删除对应区域不一致的对应关系。最后使用测地线距离进行筛选，得到置信度较高的稀疏对应关系。在此基础上使用近邻点相互匹配的方法构建剩余的每个点的对应关系。

以上算法均使用的是基于点云的局部特征的对应关系计算方法。局部的特征提取容易受到噪声的影响，且也没有考虑到三维场景上的人类视觉系统特征[10]。视觉特征是人类视觉系统的一个重要特征，它描述了人类对某个场景的注意力分布情况，因此能提取出场景中相对周围区域更独特的部分，这些区域通常对点云的对应关系构建、配准等计算具有很好的参考意义，因此本文基于文献[10]的局部和全局特征融合的特征检测，提出了一种点云的对应关系构建方法。该特征检测方法提取出原点云和目标点云在视觉上具有代表性的区域，这些区域通常都具有较高一致性。因此可以通过在这些区域间构建初始的稀疏对应关系，然后基于得到的稀疏对应关系对2个点云进行刚性配准，使2个点云的相似部位最大程度重合，来对稀疏对应关系进行最终的优化。利用得到的稀疏对应关系，使用对应关系的近邻点的局部匹配方法，为剩余的点构建对应关系。最后使用测地线距离计算对应关系的误差来进行评价。结果证明，本文方法对在人体模型上能得到较好的结果。

2 特征计算

本文方法考虑了点云的局部特征和全局特征，局部特征用于表示每个点与该点周围的差异，而全局特征的目的是用于检测整个点云模型中独特的区域，并忽略频繁出现的区域。计算步骤大致如下：1)局部特征值的计算；2)全局特征值的计算；3)局部和全局特征值非线性组合得到点云每个点最终的特征值。

局部特征值的计算使用的是快速点特征直方图(FPFH)[11]。假设点pi∈P，P是计算局部特征的点云对象，FPFH(pi)指代点pi的FPFH描述符，点pi的局部特征值D(pi)计算公式为：

(1)

其中，R指pi的用于计算的近邻点，‖pi-pj‖是指两点间的距离。χ2(pi,pj)是两点的自定义距离，其定义如下:

(2)

最后使用分段抑制函数，来防止标记过多点。最终点pi的局部特征值F(pi)为:

(3)

h是动态阈值，局部特征值按照从大到小排序后，对排名在20%以后点的局部特征值进行抑制。

全局特征值的计算的计算则是使用点云超体素化分割方法[12]将点云分割成多个像素区域，如图3所示，得到点云的像素区域集合C。设某个像素区域ci∈C，FPFH(ci)表示区域ci的FPFH描述符，该描述符定义为该区域的点的FPFH平均值。则区域ci的初始全局特征值G(ci)为：

图3 点云超体素化结果示例Fig.3 Example of VCCS results of Point Cloud

(4)

其中‖ci-cj‖是指两个像素区域的中心点的距离，χ2(ci,cj)的定义与公式(2)相同，N是指整个区域集合。

得到每个区域的初始全局特征值后，借鉴随机游走算法的思想，将每个像素区域的初始全局特征值引入到区域的每个点中。随机游动算法常用于二维图形中的分割，在待分割的图形中选取一些具有特征意义的种子点，以这些种子点为起始，通过随机游走模型，将一些属于各种子点范围内的像素挑选出来，从而完成图像的分割[13]。

在实验过程中，由于使用的点云的点数量较大，文献[10]中的全局特征计算方法通过构建整个点云的路径图来计算每个点属于某个种子点的概率，从而得到每个点的全局特征值，消耗时间较长，因此本文对全局特征值的计算做了部分改进，对于任何一个点，仅使用测地线距离最近的前几个种子点来计算该点的全局特征值，从而减少计算成本。

设置阈值h1和h2，选出特征种子点和非特征种子点。初始全局特征值大于h1的像素区域设为特征像素区域，其中心点设为特征种子点。初始全局特征值小于h2的区域设为非特征像素区域，其中心点设为非特征种子点。其中，h1和h2定义为：

h2=mean(G)

Δ=max(G)-mean(G)

(5)

对于任意没有标记为种子点的点pi，计算pi与所有种子点的测地线距离，点pi属于测地线距离最近的那个种子点，则点pi的全局特征值G(pi)为：

G(pi)=exp(-G(ci)×‖pi-ci‖×u)

(6)

其中，当点pi属于特征种子点时，u=0.1。当点pi属于非特征种子点时，u=0.001。‖pi-ci‖表示点pi与其所属种子点的距离，G(ci)表示特征点所属的像素区域的初始全局特征值。

最后，对每个点的全局特征值和局部特征值进行非线性整合。将每个点的全局特征值和局部特征值从大到小进行排序，对于全局特征值和局部特征值排名均在前20%的点，保留其中的最大值；对于全局特征值或局部特征值排名在最后20%的点，取两者的乘积；剩余情况，则取两值的平均值。

3 对应关系计算

利用得到的特征值提取出特征点集，在特征点集之间两两构建初始稀疏对应关系，然后根据FPFH距离和相关系数对初始稀疏对应关系进行初步筛选，接着使用ICP配准算法[14]进行一个粗对齐，再基于距离进行筛选，得到稀疏对应关系。然后通过稀疏对应关系的近邻点匹配的方式，计算剩余点的对应关系。

3.1 特征点选取以及初始稀疏对应关系构建

对点云的特征值进行排序，选取特征值排名在前50%的点作为备选特征点点集，并在该点集中选取特征点用于稀疏对应关系的构建。首先设置特征点点集F，以及备选特征点点集的访问队列flag，flag队列的长度为备选特征点点集长度，且初始值均为0，用于表示某个点是否被访问过。人为设置要获取的特征点数量kF。接下来的特征点选取算法步骤如下：

1)查询当前备选特征点点集中特征值最大且访问队列参数不为1的点，将该点加入特征点点集F，该点的访问队列参数设置为1；

2)以该特征点为中心，一定半径内的属于备选特征点点集的近邻点的访问队列参数设置为1；

3)如果特征点点集F的元素数量等于kF，或者访问队列参数均为1，停止，否则到步骤1。

这样就得到了点云的特征点点集，这里kF设置大小为6。然后在原点云和目标点云的特征点点集之间两两构建对应关系，也就是有kF·kF个初始稀疏对应关系。

在上一步得到初始稀疏对应关系后，需要将错误的对应删除，这里使用点的FPFH以及相关系数为每个对应关系计算一个初始权值。然后基于对应关系对原点云和目标点云进行粗刚性配准，在两者不断逼近的过程中重新计算对应关系权值，并加入空间距离，最后得到置信度较高的稀疏对应关系。

对任意点pi，利用点pi以及其近邻点构建协方差矩阵Ci，该点相关系数factor(pi)定义如下：

(7)

其λ1，λ2，λ3是矩阵Ci的特征值，λ1>λ2>λ3。

设稀疏对应关系中的一对对应关系(sj,ti)，sj和ti分别是原点云和目标点云上的一个点，这对对应关系的权值wij为：

wij=exp(-factor_dis)+exp(-FPFH_dis)

(8)

其中，factor_dis是点sj和ti的相关系数相减取绝对值，FPFH_dis是两点间的自定义距离，定义与公式(2)相同。

然后对每个对应关系的权值从大到小进行排序，本文采用[14]中的刚性配准的思想，取其中权值排名前20%对应关系，作为粗刚性配准的初始数据。

在进行了一次刚性配准后，重新计算所有对应关系的权值。计算公式如下：

wij=wij×∂1+exp(-‖sj-ti‖)·(1-∂1)

(9)

∂1是人为设定的值，这里设置为0.5，然后每个对应关系的权值从大到小重新进行排序，依旧取权值排名前5对对应关系作为下一次刚性配准的新的数据。以上过程重复进行，直至刚性配准的结果不再发生改变或者达到设置的迭代次数。在刚性配准迭代的过程中，随着2个模型逐渐重叠，距离在对应关系的权重中所占的比值会逐渐增加。此时会得到1个原点云和目标点云的相对有意义的空间位置。然后使用刚性配准方法对两者进行最后的一次配准，得到原点云和目标点云刚性部位较好重合的结果，基于这个结果，计算2个点云的特征点两两之间的距离，取距离在一定范围内并且最短的特征点作为对应点，得到最终的稀疏对应关系。

3.2 最终对应关系构建

利用已得到的稀疏对应关系，本文采用一种对应关系的近邻点相互匹配的思路为剩余的点构建对应关系，假设一对对应关系(sj,ti)，分别为原点云sj和目标点云上的点ti，搜索对应关系中各点的近邻点，得到sj和ti的近邻点集合，则sj的近邻点的对应点搜索范围则限制在ti的近邻点集合中，得到的新的对应关系又作为下一次对应关系计算的基础。这样既可以有效减少搜索空间，又可以提高准确率。该算法的步骤如下：

1)设置对应关系集合H，将已得到的稀疏对应关系放入集合H中，设置访问队列S_H和T_H，长度分别初始化为原点云和目标点云的点数量，用于表示原点云和目标点云中的点是否已经有对应点。

2)遍历关系集合H，设一对对应关系(sj,ti)∈H，sj和ti分别是原点云和目标点云上的1个点，通过kd树查询得到sj的没有对应点的近邻点集合sj_n，ti的没有对应点的近邻点集合ti_n，计算sj_n和ti_n的中每个点之间的空间距离和自定义距离(见公式(2))的和，取每个点对应和最小的点作为一对对应关系，并加入集合H。当S_H或T_H表示所有点已经拥有对应关系时，停止遍历，得到原点云和目标点云最终的对应关系集合。

4 实验结果与分析

本文使用测地线距离计算得到的对应关系的等距失真Diso。测地线距离是指曲面上2点之间的最短距离[15]。

(10)

其中，diso(sj,ti)是个体对应关系(sj,ti)对整体等距失真的贡献值：

(11)

g(sj,sm)是两点间的测地线距离。

本文使用FAUST数据集中的tr_reg_000～tr_reg_003，和SCAPE数据集中的mesh020～mesh022模型进行实验。以数据tr_reg_000作为目标点云，tr_reg_001作为原点云进行示例，由于原始数据已经是对齐状态，如图2所示，为了验证本文方法的有效性，对数据集中模型通过手工的方式，将空间相对位置全部打乱，如图4所示，左边是原点云(红)和目标点云(蓝)的原始空间相对位置，右边是人为改变后的相对位置。

图4 人为改变相对位置Fig.4 Artificial change of relative position

目标点云和原点云的特征值计算结果如图5所示，图5(A)是目标点云的特征值示意图，图5(B)是原点云的特征值示意图。从左到右分别为点云的局部特征值、全局特征值、局部和全局特征值融合结果。特征点则选取如图6所示。

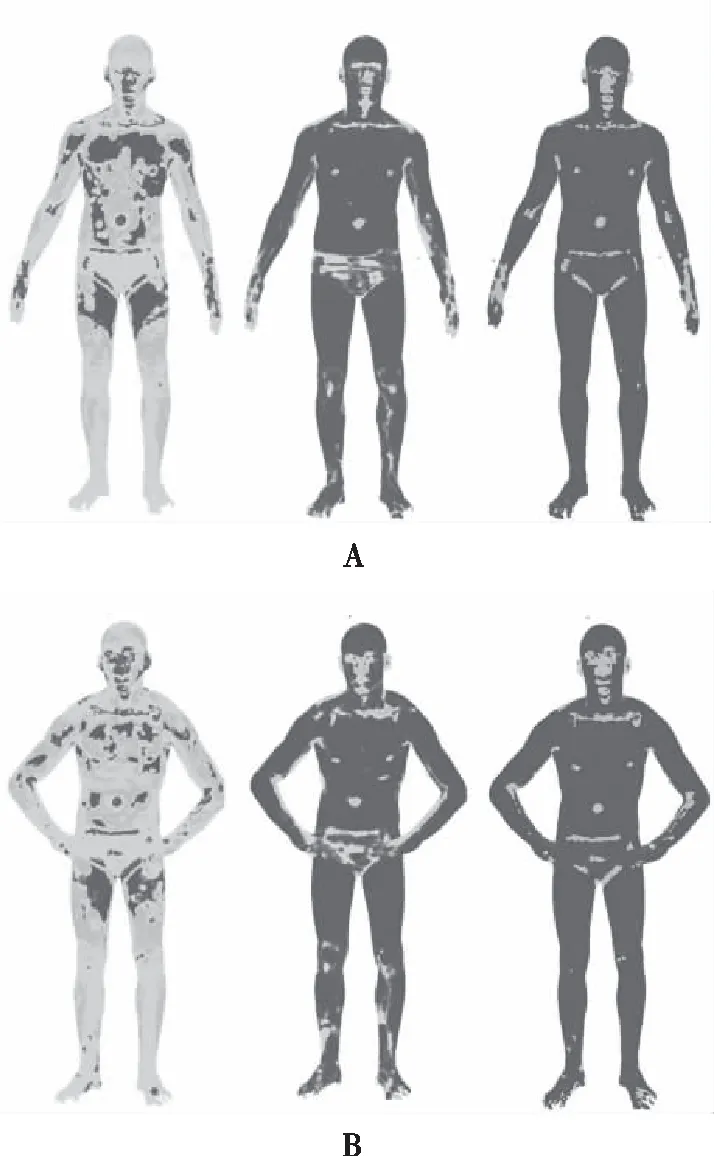
图5 特征值结果示意图Fig.5 Features results

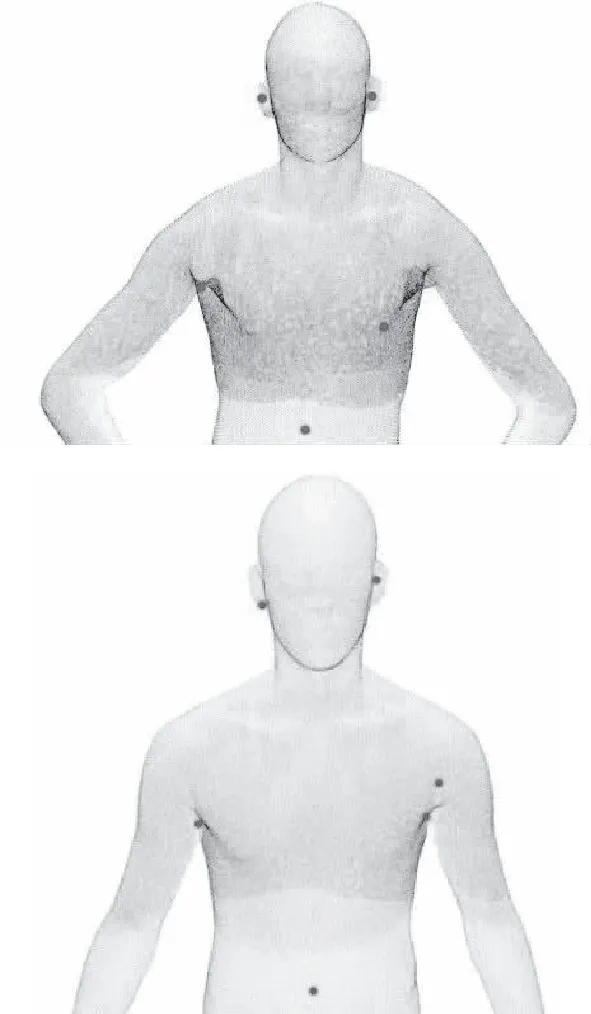
图6 特征点的选取结果Fig.6 Selection results of feature Points

两个特征点之间构建的最终稀疏对应关系如图7所示，基于稀疏对应关系的刚性配准结果如图8所示，图8(A)是本文提出的算法的计算结果，图8(B)是传统ICP算法的计算结果。为验证本文改进的ICP算法的有效性，设置了以下几组实验数据，如图9所示，其中，红色为目标点云，蓝色为原点云，配准结果通过均方根误差RMSE评价，该误差定义如下：

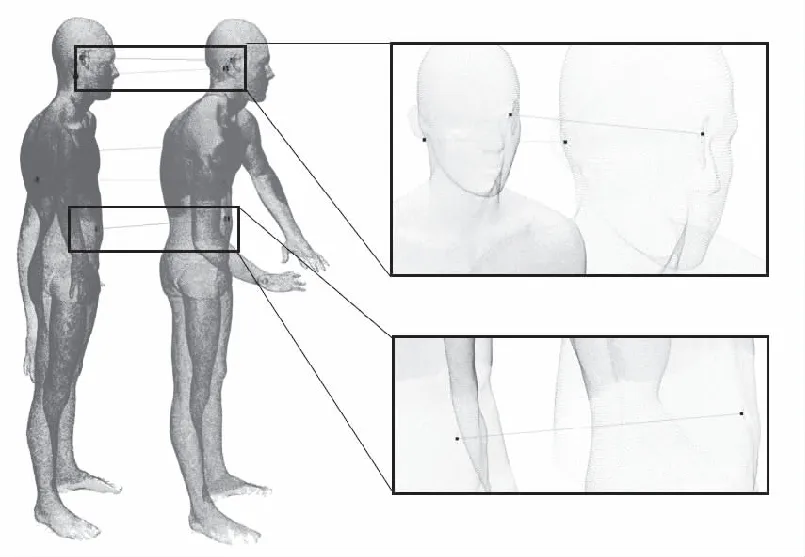
图7 稀疏对应关系计算结果示意图Fig.7 Coarse Correspondence results

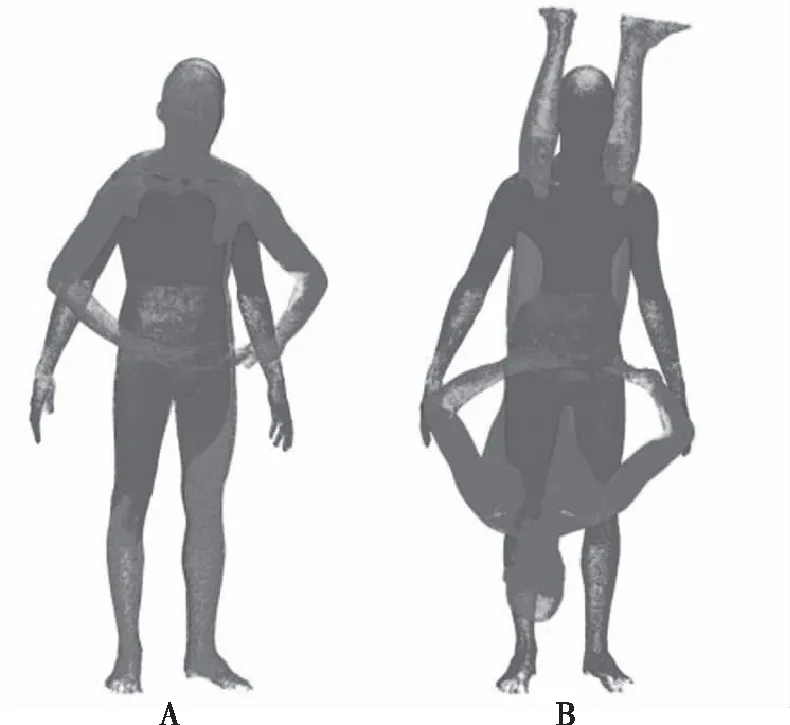
图8 配准结果Fig.8 Registration results

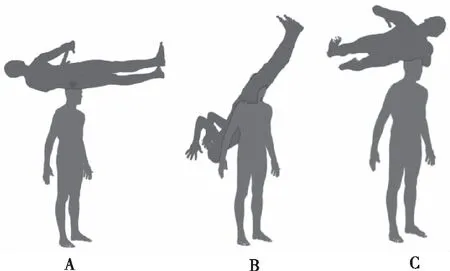
图9 配准前的相对位置Fig.9 Relative position before registration

(12)

其中，qi表示原点云上的一点，pj是qi的对应点，‖qi-pj‖表示两点间的欧氏距离。一般来说，当值小于0.008时，结果是可靠的。本文方法的对齐效果如图10所示，传统ICP方法的对齐效果如图11所示，误差如表1所示，可以看出，当模型位置差异较大时，本文方法能得到一个较好的对齐结果。因为传统ICP算法是通过最近点搜索得到对应关系，在此基础上进行配准，当模型的动作差异较大时，效果较差，本文在传统ICP方法的基础上计算了比较可靠的稀疏对应关系作为前置条件，因此能得到较好的配准结果。

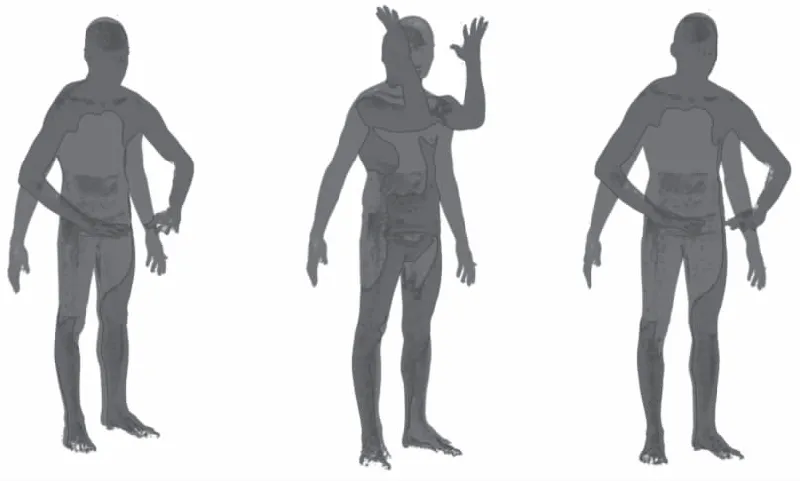
图10 本文配准结果Fig.10 Our registration results

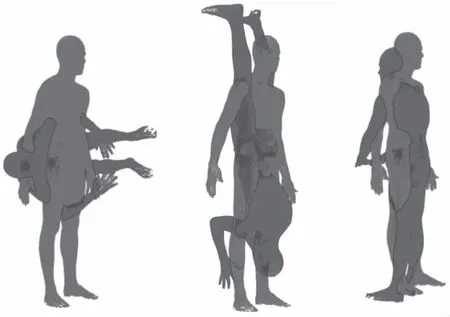
图11 传统ICP配准结果Fig.11 ICP registration results

表1 刚性配准结果评价Tab.1 Evaluation of registration results

点云剩余点的对应关系计算过程示意如图12所示，图12(A)是已经计算得到的对应关系，图12(B)是通过对应关系之间的近邻点匹配构建新的对应关系，图12(C)展示了部分最终计算得到的对应关系结果。以FAUST数据集的tr_reg_000为目标点云，tr_reg_001～tr_reg_003为原点云，其对应组分别为a、b、c。以SCAPE数据集的mesh020为目标点云，mesh021和mesh022为原点云，其对应组分别为d和e，最终对应关系计算结果如图13所示，以上几组模型的对应关系结果的等距失真如表2所示，同时将本文方法与文献[5]、文献[6]的方法进行了对比。由于文本方法依赖于配准结果，所以当原点云和目标点云拥有较少形变部分的情况下，如实验组a、b、c和d，能取得较好的结果，但是在实验组e上结果较差。而文献[5]与文献[6]的方法主要依赖于点云的特征描述，因此在面对不同形变程度的模型时，结果相对比较稳定。

表2 对应编号的点云对应关系各项评价数据Tab.2 Evaluation of Point Cloud Correspondence

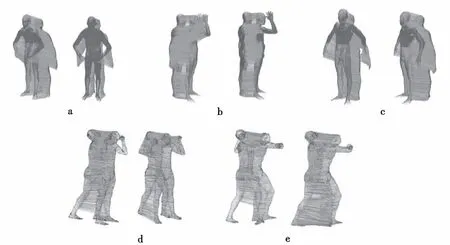
图13 最终对应关系计算结果示意图Fig.13 Results of final Correspondence

5 结束语

本文提出了一种基于局部和全局特征融合进行特征检测的方法来计算点云对应关系的方法，该方法能够稳定的获得原点云和目标点云的具有较高一致性的特征区域，从而为后续获得较可靠的稀疏对应关系提供了良好的条件，且只需要拥有坐标数据的点云就可自动实现，不需要额外的信息。通过在不同几个数据组上的实验结果表明，本文方法在形变程度不是很大的人形点云数据上表现较好。由于本文方法比较依赖于刚性配准的结果，在应对形变程度较大的点云数据时表现不理想，因此，本文方法在配准这一步还有改进的空间。