基于隔离型模块化多电平换流器的中压直流柔性互联配电系统稳定性分析

秦健飞，裴忠晨，林 琳，刘 闯，朱 帝，王菁月，聂宏展

（1.东北电力大学 电气工程学院，吉林 吉林 132012；2.浙江华云清洁能源有限公司，浙江 杭州 310000）

0 引言

随着我国“双碳”目标的提出，以光伏、电动汽车为代表的新型源／荷广泛接入已成为我国城市能源互联网发展建设的重要特征。一方面，具有间歇性、随机性的分布式电源使传统配电网从“有限电源”向“泛在电源”转变，改变了电网潮流分布与系统运行特性，配电网双向潮流调控面临着新的挑战［1-3］；另一方面，大规模具有冲击性、无序性的直流充电负荷对配电网容量造成了巨大压力，导致本地电力电量供需不平衡［4］。

中压直流（medium voltage direct current，MVDC）柔性互联配电系统凭借光伏／风电等分布式电源可潮流调控、电动汽车等直流型负荷可灵活接纳、供电容量大、功率变换环节少、供电可靠性高等优势，成为未来城市能源互联网的新型配电技术方案［5-6］。然而MVDC柔性互联配电系统内部缺少旋转设备，系统惯性小，容易引发各类振荡甚至诱发失稳，造成重大经济损失［7］。因此，研究MVDC柔性互联配电系统的稳定性十分必要。

实际MVDC柔性互联配电系统中出现的各类振荡大多归因于系统参数缓慢变化，可定性为小扰动失稳［8］。状态空间法和阻抗分析法是目前常用的2类直流配电系统小扰动稳定性的建模和分析方法。相比于状态空间法，阻抗分析法具有物理意义清晰、可以直接测量等优势，在分析复杂系统的稳定性问题中更加简单有效。文献［9］推导了具有主动孤岛检测方案的分布式电源的输出阻抗模型，讨论了系统阻抗之间的相互作用；文献［10-11］提出单级统一阻抗建模方法，克服了双级式直流变压器系统模型的构建问题；文献［12］提出了一种适用于MVDC和低压直流（low voltage direct current，LVDC）配电系统的级联系统，并分析了其小信号阻抗稳定性。

在MVDC柔性互联配电系统中，随着具有多时间尺度特性的电力电子设备接入，系统易产生振荡，其中低频振荡问题严重威胁系统的安全稳定运行［13］。针对直流微电网和直流配电系统的低频振荡问题，国内外众多学者已展开大量研究。文献［14］指出低压柔性直流配电系统中换流器与恒功率负载的相互作用会产生低频振荡，提出利用有源抑制方法研究系统的谐振机理；文献［15］研究了并网逆变器接入柔性直流配电系统可能存在的低频振荡现象；文献［16］分析了柔性直流输电系统低频振荡的机理并提出一种谐波抑制策略；文献［17］针对电动机动态负荷接入柔性直流配电系统的低频振荡问题，提出了2种不同的稳定补偿方法。目前对基于隔离型模块化多电平换流器（isolated modular multilevel converter，IMMC）的MVDC柔性互联配电系统的稳定性分析尚未见报道。

本文基于文献［18］提出的IMMC构建MVDC柔性互联配电系统。与传统级联H桥型模块化多电平换流器的双级式拓扑结构相比，IMMC采用单级式功率变换结构，消除了双级式拓扑结构所需的独立电容，无需复杂的均压控制，减小了设备体积，降低了设备成本并提高了系统稳定性。首先分别建立了IMMC的LVDC侧、MVDC侧和中压交流（medium voltage alternating current，MVAC）侧的小信号模型以及控制系统的小信号模型，分析了各端口的阻抗特性，得到IMMC的整体小信号模型，进而推导出MVDC侧的阻抗模型。然后建立了MVDC柔性互联配电系统的等效电路，采用阻抗分析法分析了电路参数和控制器参数对阻抗特性以及系统稳定性的影响。最后，基于MATLAB／Simulink搭建MVDC柔性互联配电系统仿真模型，验证了所建MVDC侧阻抗模型的正确性以及MVDC母线电压稳定运行与振荡失稳理论分析的准确性。

1 MVDC柔性互联配电系统结构

MVDC柔性互联配电系统内部选用2台IMMC作为柔性电气节点，经±10 kV MVAC馈线实现2个10 kV和20 kV的交流电网互联，该设计可满足现有交流配电网的容量需求。LVDC母线连接光伏、储能系统、电动汽车等，构成LVDC微电网。MVDC柔性互联配电系统结构图见附录A图A1。

1.1 三相IMMC拓扑结构

三相IMMC具有LVDC、MVAC和MVDC这3个端口。三相IMMC的每一相包含上、下2个桥臂以及交流滤波电感L0，其中每个桥臂由n个子模块和1个桥臂电感Lm构成，每个桥臂的高频隔离型子模块使用输入并联输出串联的连接方法，在一次侧并联构成LVDC端口，在二次侧串联连接MVDC端口和MVAC端口。三相IMMC拓扑结构见附录A图A2。

1.2 配电系统控制方法及子模块调制策略

本文采用的双调制自由度协调控制方法可以通过独立调整交流调制比和直流调制比实现对交、直流端口的独立解耦控制。由于IMMC采用单级式结构，消除了双级式结构中子模块的独立电容，因此无需考虑复杂的前、后级协调控制策略以及均压控制策略，只需分别控制各个端口即可。基于IMMC的MVDC柔性互联配电系统的控制策略见附录A图A3。

本文IMMC上、下桥臂子模块采用载波移相脉宽调制策略，其可以通过较低的开关频率得到较高的等效开关频率，提高输出波形的质量，减小损耗。上、下桥臂子模块调制策略的数学模型可表示为：

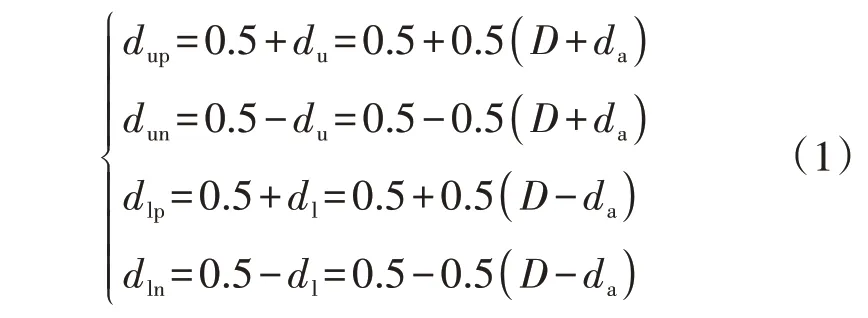
式中：dup、dlp和dun、dln分别为上、下桥臂子模块超前和滞后的调制信号；du、dl分别为上、下桥臂的占空比；D为直流调制比；da为交流调制比。

2 IMMC小信号模型

为了简化分析，本文假设三相电力系统各相平衡，忽略开关损耗和线路损耗。以A相为例，上、下桥臂每个高频隔离型子模块使用交直流混合调制比，当忽略桥臂不平衡的情况时，上、下桥臂交流调制比相同。如果不考虑变压器漏感和桥臂漏感，则A相上桥臂电压uAu和A相下桥臂电压uAl可分别表示为：

式中：k为高频隔离变压器一、二次侧绕组匝数比；daA为A相交流调制比；udcL为LVDC侧电压。

基于以上分析，首先推导IMMC的平均模型，并对模型进行线性化，分别建立IMMC的MVAC、LVDC及MVDC侧的小信号模型，进而得到IMMC系统的小信号模型，为建立MVDC侧阻抗模型奠定基础。

2.1 MVAC侧小信号模型

根据基尔霍夫电压定律分别列出A相上、下桥臂电压方程，然后经过化简变换得到dq坐标系下MVAC侧的平均模型，如式（4）所示（详细推导过程见附录A式（A1）—（A9））。

式中：id、iq和ud、uq分别为三相电流、电压的d、q轴分量；dad、daq分别为交流调制比的d、q轴分量；R0、Rm分别为交流滤波电阻、桥臂电阻；ω为电网角频率。

此时平均模型为时不变模型，但仍非线性，不能用于阻抗模型的推导，因此必须建立线性化的小信号模型。基于系统的某个稳定的直流工作点，在该点周围的1个小区域内进行局部线性化，以得到局部线性化模型［19］。假设系统(x，u)的某个稳定的直流工作点为(，)（后文以带“-”变量表示对应变量的稳态值），在其附近加入小信号扰动(，（)后文以带“ˆ”变量表示对应变量的小信号分量），此时各变量为稳态分量和小信号分量之和，即x=+^，u=+。

将式（4）中各变量用稳态分量和小信号分量之和替换，并忽略扰动的平方项，得到MVAC侧的小信号模型，如式（5）所示。

2.2 LVDC侧小信号模型

根据基尔霍夫电流定律对LVDC侧电容节点处列出电流方程为：

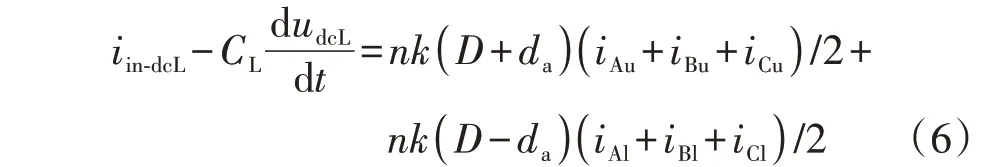
式中：iju、ijl（j=A，B，C）分别为流过j相上、下桥臂的桥臂电流；iin-dcL为LVDC侧输入电流；CL为LVDC端口稳压电容。

以A相为例，iAu、iAl与MVDC电流idcM和MVAC电流iA之间的关系如式（7）所示。

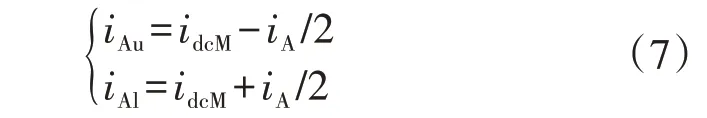
将式（7）代入式（6），整理化简可得：

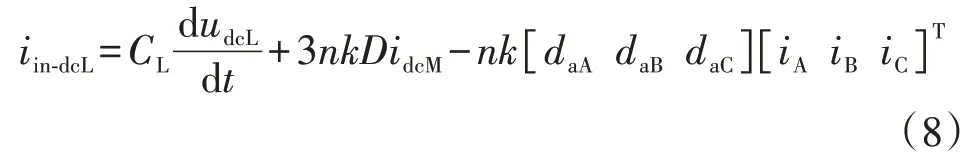
式中：ij为j相电流；daj为j相交流调制比。对式（8）进行dq变换可得：

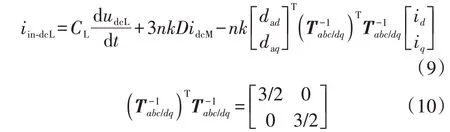
根据式（9）、（10）可得dq坐标系下LVDC侧输入电流iin-dcL为：

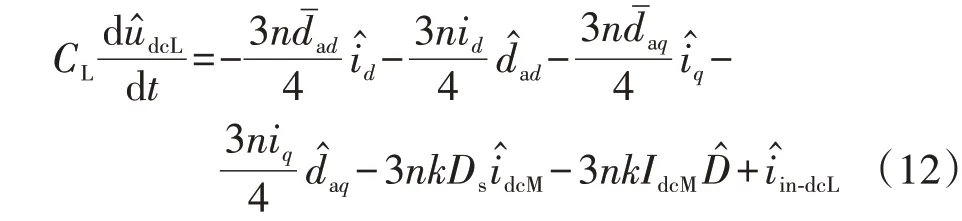
2.3 MVDC侧小信号模型

在MVDC侧分别列写基尔霍夫电压、电流定律方程可得：

式中：uju、ujl分别为j相上、下桥臂的桥臂电压；CM为MVDC端口稳压电容dcM为MVDC侧三相电压稳态值；udcM为MVDC侧电压为MVDC侧注入的小扰动电流。

类似地，可得MVDC侧小信号模型为：

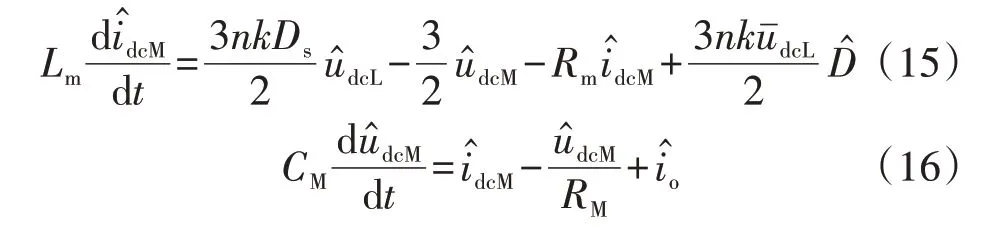
2.4 控制系统小信号模型

MVAC侧控制器采用功率外环、电流内环进行设计。MVDC侧控制器采用电压外环和功率外环配合的主从控制策略，一端采用定电压控制，另一端采用定功率控制，两侧端口外环将产生的电流参考值输入各自的电流内环，最终输出MVDC两侧端口各自的直流调制比。

MVAC侧端口的功率外环控制方程为：MVAC侧端口的电流内环控制方程为：

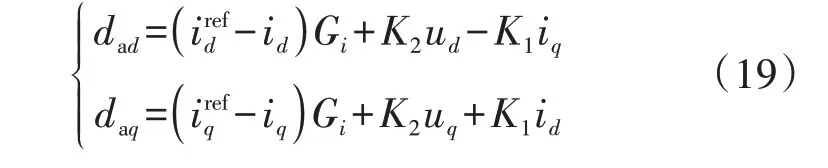
式中：Gi为MVAC侧端口的电流内环控制器传递函数，由比例系数kip和积分系数kii组成，Gi=kip+kii/s；K1为id、iq的增益系数；K2为ud、uq的增益系数。式（19）的小信号模型为：

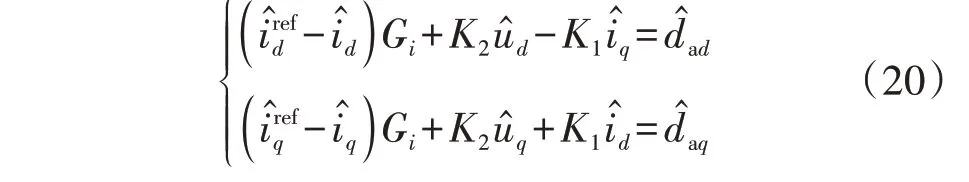
MVDC输出侧源变换器的电压外环控制方程为：

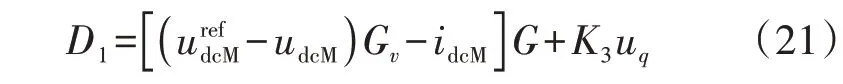
式中：Gv为电压外环控制器传递函数，由比例系数kvp和积分系数kvi组成，Gv=kvp+kvi/s；G为MVDC输出侧源变换器的电流环控制器传递函数，G=kp+ki/s；urefdcM为udcM的参考值；K3为MVDC侧电压的增益系数。式（21）的小信号模型为：

MVDC输入侧负载变换器的功率外环控制方程为：

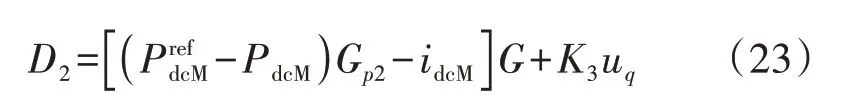
式中：Gp2为功率外环控制器传递函数，由比例系数kp2p和积分系数kp2i组成，Gp2=kp2p+kp2i/s；P为MVDC侧负载变换器输入的有功功率PdcM参考值。式（23）的小信号模型为：

2.5 IMMC小信号模型

综上所述，结合所得到的LVDC、MVDC以及MVAC侧小信号模型，可以进一步得到IMMC的小信号模型，如附录A图A4所示。

3 MVDC柔性互联配电系统阻抗模型及验证

在所建IMMC小信号模型的基础上，推导得到MVDC侧阻抗模型，通过绘制阻抗的Bode图分析MVDC柔性互联配电系统各端口特性，进而采用奈奎斯特稳定判据对基于IMMC的MVDC柔性互联配电系统稳定性展开分析，并以此为理论依据指导控制器参数的设计。

3.1 MVDC侧输出阻抗模型

式中：A1（t）、B1（t）、C1（t）的表达式分别见附录A式（A10）—（A12）。则MVDC侧端口的输出阻抗Z1_out为：

式中：I为单位矩阵。

3.2 MVDC侧输入阻抗模型

3.3 直流线路阻抗模型

目前学者通常采用π型线路模拟实际的直流线路，附录A图A5给出了π型直流线路等效模型。由于π型线路模型的分布电容Cline较小，因此可以将两侧分布的均匀电容整合到线路两端变换器接口的输出电容中，故计算直流线路阻抗时可以忽略分布电容，线路阻抗Zline可以表示为：

式中：Rline为线路电阻；Lline为线路电感。

3.4 MVDC柔性互联配电系统等效电路

为了对MVDC柔性互联配电系统进行稳定性分析，在获取阻抗模型后，需要用线性网络结构表示该交互系统的等效电路，然后再采用阻抗稳定判据来分析系统稳定性。图1为MVDC柔性互联配电系统小信号等效电路图。图中：Ig()s为线路电流；Ueq1_out、Ieq2_in分别为MVDC输出侧的等效电压源和MVDC输入侧端口的等效电流源。

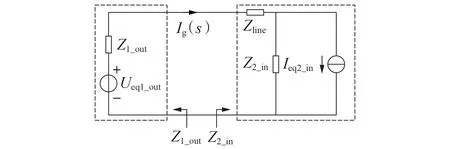
图1 MVDC柔性互联配电系统等效电路Fig.1 Equivalent circuit of MVDC flexible interconnected power distribution system

在分析级联系统稳定性时，Ig(s)可表示为：

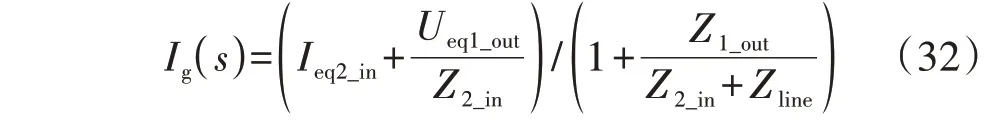
式（32）中当源变换器和负载变换器都能稳定运行时，Ig(s)的稳定性取决于1/[1+Z1_out/(Z2_in+Zline)]。故只有Z1_out/(Z2_in+Zline)满足奈奎斯特判据，才能保证MVDC柔性互联配电系统的稳定性。定义阻抗比Tm为：

式中：Z′2_in=Z2_in+Zline。

3.5 阻抗模型验证

为了验证上述阻抗模型的正确性，按照附录A表A1的系统参数基于MATLAB／Simulink软件搭建了基于IMMC的MVDC柔性互联配电系统时域仿真模型。阻抗测量的基本方法有电压扰动注入法和电流扰动注入法2种，本文采用电流扰动注入法验证阻抗模型的准确性。在MVDC侧采用电流扰动注入法，利用扰动电流和响应的扰动电压计算MVDC侧的输出阻抗。附录A图A6给出了具体的电流扰动注入的测量方式，注入幅值为1 A、频率变化范围为［5，9 000］Hz的扰动电流源i^dc。

利用MATLAB做出MVDC柔性互联配电系统的MVDC侧输出阻抗Z1_out和MVDC侧输入阻抗Z2_in的Bode图，并通过仿真系统测量2个端口实际阻抗Bode图，如附录A图A7、A8所示。观察其幅频特性曲线与相频特性曲线，仿真结果与理论分析结果基本吻合，证明了本文所推导MVDC侧阻抗模型的正确性，因此该模型适用于从低频段到高频段MVDC柔性互联配电系统的稳定性分析。

4 MVDC柔性互联配电系统小信号稳定性分析

在MVDC柔性互联配电系统中，MVDC侧阻抗受电路参数和各个控制环节调节器参数的影响，本文采用奈奎斯特稳定判据分析参数对基于IMMC的MVDC柔性互联配电系统稳定性的影响。当输入阻抗比Tm的奈奎斯特曲线不包含点（-1，0）时，系统稳定。

4.1 稳压电容

MVDC输出侧源变换器的稳压电容CM1变化时Tm的奈奎斯特曲线见附录B图B1。当CM1逐渐增大时，Tm的奈奎斯特曲线开始向单位圆内收缩，其幅值裕度逐渐增大，这说明CM1增大有利于MVDC柔性互联配电系统的稳定。

MVDC输入侧负载变换器稳压电容CM2变化时Tm的奈奎斯特曲线见附录B图B2。当CM2增大时，Tm的奈奎斯特曲线靠近点（-1，0），MVDC柔性互联配电系统的稳定裕度减小，系统会逐渐趋于不稳定，这说明MVDC柔性互联配电系统可能会因CM2设置不合理而引发低频振荡现象。

4.2 桥臂参数

桥臂电感Lm1变化时Tm的奈奎斯特曲线见附录B图B3。随着Lm1的增大，Tm的奈奎斯特曲线越远离点（-1，0），MVDC柔性互联配电系统的稳定裕度增大，越有利于系统的稳定。

4.3 MVDC端口电压外环控制参数

kvp变化时Tm的奈奎斯特曲线见附录B图B4。当kvp=0.12时，Tm的奈奎斯特曲线包围点（-1，0），此时系统不稳定，当其增加到0.13时，没有包围点（-1，0），此时系统刚刚达到稳定状态。说明随着kvp的增大，Tm的奈奎斯特曲线越远离点（-1，0），MVDC柔性互联配电系统的稳定裕度增大，有利于系统的稳定。

kvi变化时Tm的奈奎斯特曲线见附录B图B5。随着kvi的增大，Tm的奈奎斯特曲线开始向单位圆内收缩，其幅值裕度逐渐增大，有利于MVDC柔性互联配电系统的稳定。

4.4 MVDC端口电流内环控制参数

kp变化时Tm的奈奎斯特曲线见附录B图B6。随着kp的增大，奈奎斯特曲线越靠近点（-1，0），MVDC柔性互联配电系统的稳定裕度减小，系统逐渐趋于不稳定。

ki变化时Tm的奈奎斯特曲线见附录B图B7。随着ki的增大，Tm的奈奎斯特曲线开始向单位圆内收缩，MVDC柔性互联配电系统的稳定裕度逐渐增大，使系统趋于稳定。

4.5 直流线路阻抗

直流线路阻抗变化时Tm的奈奎斯特曲线见附录B图B8、B9。线路电阻增加时，Tm的奈奎斯特曲线逐渐向单位圆内收缩，幅值裕度不断增大；而当线路电感持续增加时，Tm的奈奎斯特曲线逐渐向左侧移动，并且在线路电感为0.4 mH时奈奎斯特曲线包围点（-1，0），级联系统出现不稳定。

4.6 MVAC侧功率外环控制

MVAC侧功率外环PI参数变化时Tm的奈奎斯特曲线见附录B图B10。当MVAC侧功率外环控制器参数逐渐增大时，Tm的奈奎斯特曲线保持不变，这说明MVAC端口功率外环控制器参数对MVDC侧几乎没影响，因此本文不再分析其对稳定性的影响。

5 MVDC母线电压稳定性分析

第4节分析了电路参数和控制器参数对MVDC柔性互联配电系统稳定性的影响，分析可得电容CM2、电压环比例系数kvp、电压环积分系数kvi以及电流环积分系数ki1对MVDC互联系统稳定性的影响规律，因此本节主要验证以上参数变化对MVDC母线电压稳定性的影响。

［0，0.3）s时，系统处在稳定状态，当系统稳定运行到0.3 s时，只改变电压环积分系数kvi，使kvi从0变化到0.1，得到Tm的奈奎斯特曲线如附录C图C1所示。由图可知，Tm的奈奎斯特曲线未包围点（-1，0），此时系统仍稳定运行。MVAC侧的电流波形、MVAC侧电流快速傅里叶变换（fast Fourier transform，FFT）分析以及LVDC侧波形分别见附录C图C2—C4，MVDC母线电压波形和其FFT分析结果分别如图2、3所示，系统仍能稳定运行，MVDC母线电压未发生振荡。

图2 稳定运行下的MVDC母线电压波形Fig.2 Waveform of MVDC bus voltage under stable operation

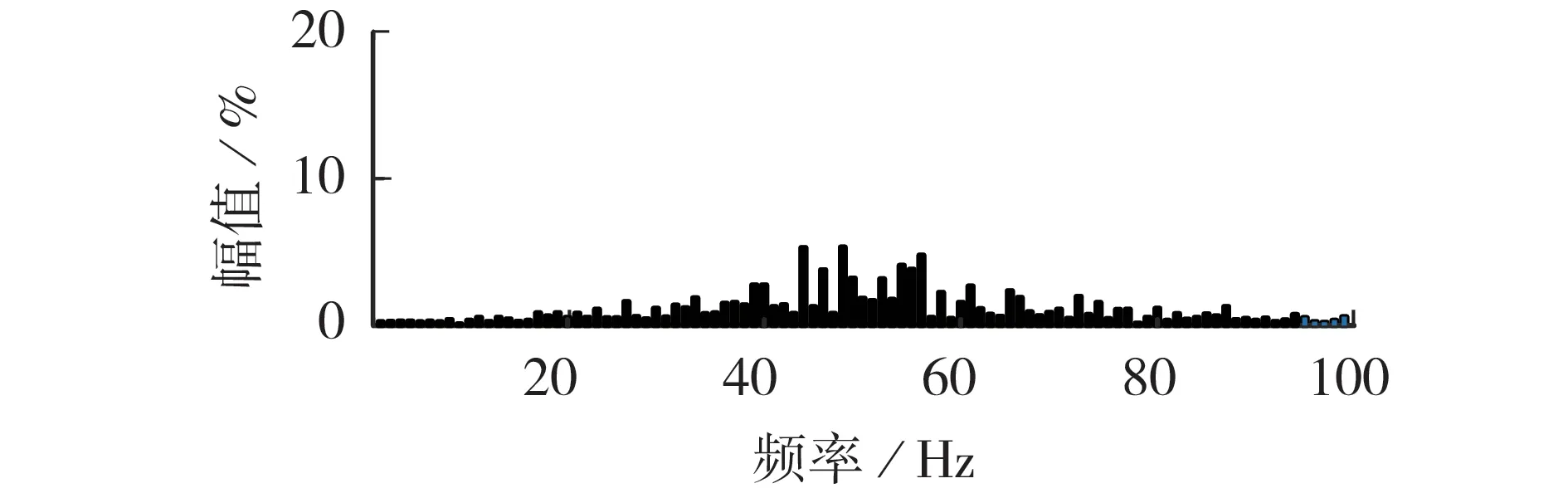
图3 稳定运行下的FFT分析结果Fig.3 FFT analysis result under stable operation

当CM2从0.6 mF变化到0.8 mF，kvp从0.2变化到0.1，kvi从0变化到0.1，ki1从0.008变化到0.000 1时，Tm的奈奎斯特曲线如附录C图C5所示。可以看出Tm的奈奎斯特曲线与单位圆存在交点，交点频率为12.3 Hz，此时该系统有发生低频振荡的风险。MVAC侧的电流波形、MVAC侧电流FFT分析以及LVDC侧波形图分别见附录C图C6—C8，MVDC母线电压振荡波形及其FFT分析结果分别如图4、5所示，其振荡频率集中在13 Hz，与理论分析相符，进一步证明了所建模型的正确性。

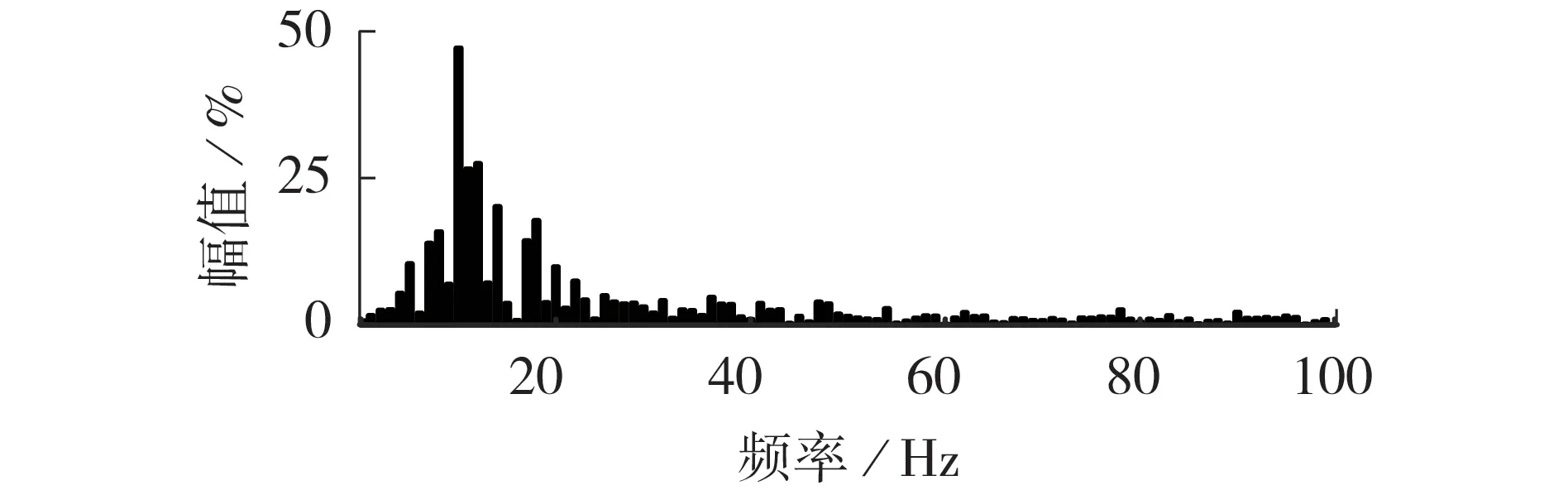
图5 振荡模式下的FFT分析结果Fig.5 FFT analysis result under oscillation mode

图4 振荡模式下的MVDC母线电压波形Fig.4 Waveform of MVDC bus voltage under oscillation mode

6 结论

本文以IMMC作为关键装备构建MVDC柔性互联配电系统，并采用阻抗分析法针对MVDC柔性互联配电系统的稳定性展开研究，得出以下结论。

1）理论阻抗模型与仿真测量结果吻合度较高，验证了本文所建基于IMMC的MVDC侧阻抗模型的正确性，并利用所建精确模型进一步研究基于IMMC的MVDC柔性互联配电系统阻抗特性及其主要影响因素。

2）分析了MVDC柔性互联配电系统中电路参数和控制器参数对于稳定性的影响。负载变换器电压环比例积分参数、电流环积分参数、线路电感的减小或者MVDC侧稳压电容的增大可能会导致系统不稳定，并在互联系统发生振荡时，可以通过控制器参数优化设计对互联系统谐振现象进行抑制。

3）揭示了不同参数对端口阻抗特性与MVDC柔性互联配电系统稳定性的影响程度，为IMMC控制系统参数优化设计提供了理论依据，对基于IMMC的MVDC互联柔性配电系统稳定运行具有指导意义。

附录见本刊网络版（http：//www.epae.cn）。