串联式捞渣机器人运动学分析及ADAMS 仿真

李源，罗璟，袁安华，余长顺

（650500 云南省 昆明市 昆明理工大学 机电工程学院）

0 引言

在金属产品的冶炼生产过程中会生成一种影响产品质量的副产物——浮渣，它的产生是不能避免的。为了减少浮渣的生成量，除了需要严格控制金属液的处理时间、金属液的温度、锅炉的停车次数和时间等生产过程中的参数以外，最主要的就是使用外部设备（如除渣机器人等）来对金属液进行定期的除渣工作，这样可以使金属液中的浮渣含量保持在一个相对稳定的范围内。

目前，国内主要是通过工人手持简易自制捞渣斗，捞取锌冶炼锅中的氧化渣。人工捞渣存在诸多问题，如捞渣不迅速不完全、效率不高、工作强度大、危害风险比较高等。工人如若不能及时彻底将氧化渣捞除，就会对镀锌板表面质量产生影响；捞渣效率低则会对镀锌生产线的自动化水平以及生产效率产生影响。人工捞渣要求工作人员在高温有毒环境中工作比较长的时间，大大增加了工人的工作强度以及受危害的风险程度[1]。另外，人工捞渣会使锌液泛起波纹，导致涂层厚度不一致，严重影响镀锌产品质量。锌锅动荡增多则会增加锌液与空气的接触，生成更多氧化物，使表面产生更多缺陷[2]。

为了提高捞取锌渣的效率，降低工人的工作强度，在参考国内外捞渣机器人设计的基础上，本文根据邹慧君[3]和钟毅芳[4],吴昌林等文献的基本原理，设计了一种串联式捞渣机械臂，可以在恶劣工况下工作。文中运用SolidWorks 软件对捞渣机械臂的三维模型进行简化，对打捞机器人正逆运动学进行分析，通过ADAMS 软件对机械臂进行运动学仿真，得出末端法兰的速度、加速度，进而说明本设计的合理性。

1 移动式捞渣机器人建模及运动学分析

1.1 机器人D-H 坐标系的建立及相关参数

移动捞渣机器人（如图1）系统由2 部分组成，第1 部分是6 轴串联机器人，第2 部分是线性导轨式滑台。对导轨移动式捞渣机器人采用改进的D-H方法建立的坐标系如图2 所示。图2 中，7 号表示移动平台的移动关节，1 到6 号分别表示机器人本体结构中6 个转动关节，坐标系{0}是基础坐标，实际上它和坐标系{7}是相互重合的，在建立的D-H坐标系中，起始末端点坐标为[825.5，0，1 080]。建立移动捞渣机器人的基坐标系{0}，设定基座参数分别为α0=0，a0=0，θ0=0°，d0=0°，通过坐标变换可得机器人连杆参数，具体参数如表1 所示。

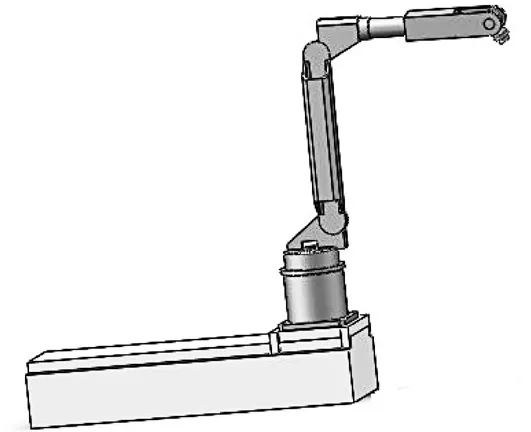
图1 移动捞渣机器人示意图Fig.1 Schematic diagram of mobile slag removing robot

图2 移动捞渣机器人的D-H 坐标系Fig.2 D-H coordinate system of mobile slag removing robot

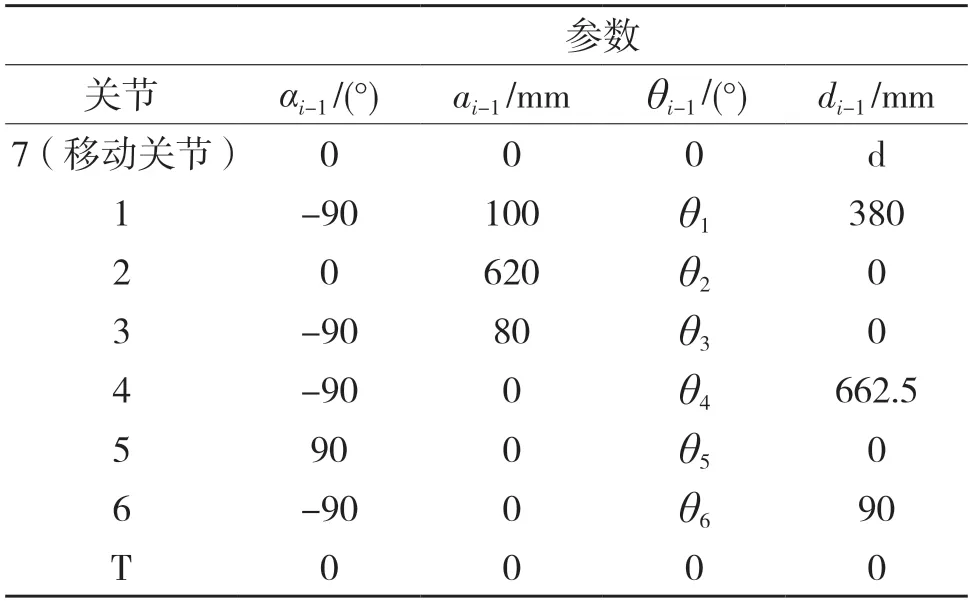
表1 捞渣机器人的D-H 参数表Tab.1 D-H parameters of slag robot

1.2 捞渣机器人的正运动学分析

通过建立捞渣机器人的D-H 连杆坐标系[5]，可以对机器人的每一个关节进行坐标旋转变换和平移变换，这样就可以得到捞渣机器人的末端位姿在世界坐标系里面的位姿矩阵。下述过程是将相互邻接的两连杆之间的矩阵进行齐次变换。Aij 为变换矩阵，它表示的是将坐标系{i}变到{j}，对每一个关节坐标系都可以进行相应的矩阵转换，这样就可以得到式（1）—式（9）的转换矩阵：

移动式捞渣机器人的正运动学表达式如式（9）所示。式中，ci表示的是cosθ，si表示的是sinθ；式（9）中，Ni，Oi，Pi（i=1，2，…）则是关于连杆变量D、θi（i=1，2，3，4，5，6）的函数。

1.3 基于Robotics Toolbox 的正运动学分析仿真验证

为了验证上述的捞渣机器人运动学分析是否正确，使用 MATLAB 中的Robotics Toolbox 工具箱对其进行求解。工具箱中的 fkine 函数可以对机器人的末端位姿求解，如果机器人的末端位姿q=[0-pi/2 0 0 0 0]，则对应的变换矩阵为T=fkine（r，q）。图3 所示为求解的程序以及结果。

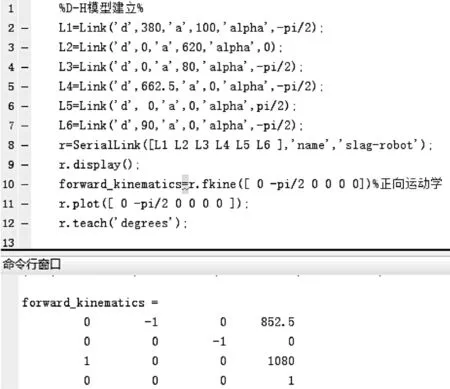
图3 MATLAB 求解末端矩阵Fig.3 MATLAB solution of terminal matrix

将θ1=0，θ2=-pi/2，θ3=0，θ4=0，θ5=0，θ6=0 代入式（9），求解机器人末端变换矩阵如式（10）所示。

比较发现，由矩阵变换求解出来的结果与fkine 函数求解出来的结果是一致的，结果证明机器人的 D-H 建模以及正运动学分析是正确的。

2 仿真模型的建立

采用ADAMS 2016 对移动式捞渣机器人进行运动学仿真分析 。具体运动学仿真分析步骤如下：

（1）对模型进行简化并导入ADAMS

参考国内捞渣机器人设计的经验[7]，由于本文在设计移动式捞渣机器人结构部件时没有考虑齿轮轴承等部件，只是简化后的机器人，因此可以直接导入 ADAMS 。需要注意的是，通过SolidWorks进行仿真模型转换时2 个软件之间的单位以及坐标系应该是统一的，这样才能确保数据之间转换正确。打开ADAMS 软件，创建一个新的模型，将SolidWorks 软件导出的parasolid.x_t 格式的文件导入，如图4 所示。移动式捞渣机器人导入后的结构模型如图5 所示。

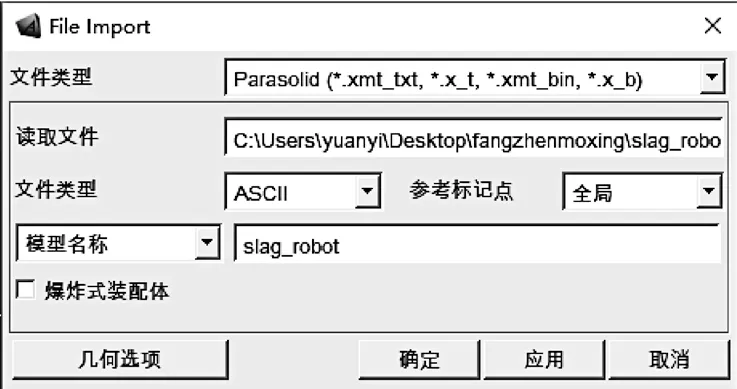
图4 捞渣机器人导入到 ADAMSFig.4 Slag removing robot imported into ADAMS

图5 移动式捞渣机器人的结构模型图Fig.5 Structure model diagram of mobile slag removing robot

（2）对机器人创建约束并添加驱动

在移动式捞渣机器人模型中，有固定不动的刚体，也有通过转动副或移动副相互连接的刚体。机器人底座和移动平台的滑块是固定的，轨道和大地之间固定在一起，它们之间添加为固定副；轨道与滑块之间可以移动，添加的是移动副；其余各关节之间均添加转动副。通过ADAMS 中的STEP 函数完成对机器人驱动的添加，完成约束以及驱动的添加之后，捞渣机器人的模型如图6 所示。

图6 移动式捞渣机器人的模型结构Fig.6 Model structure of mobile slag removing robot

（3）对仿真模型进行验证

运行仿真前，要求对前面处理好的仿真模型进行检验，特别是存在较多约束和驱动的仿真模型，这样可以查看约束和驱动的具体添加情况，避免出现由于过约束或者欠约束致使仿真过程失败。在工具中单击验证模型选项，本文模型验证是成功的。

（4）进行仿真求解

完成上述的操作过程之后，运用STEP 函数进行仿真，仿真时间设置为7 s，仿真步数设置为300，运行仿真。

（5）仿真结果的后处理

仿真计算完成之后，可以在结果选项中查看结果以及进行后处理操作，输出需要的曲线图。

3 仿真结果分析

图7 是捞渣机器人末端法兰位移的变化曲线图，从图中可以分析看出，捞渣机器人的位移变化曲线比较平滑，表示机器人在给定的轨迹中运行平稳，没有发生突变，说明机器人是可以达到实际工作要求的。

图7 捞渣机器人末端法兰位移的变化曲线Fig.7 Variation curve of end flange displacement of slag removing robot

图8 是捞渣机器人末端法兰的速度变化曲线，图9 是捞渣机器人末端法兰加速度变化曲线，图10 是捞渣机器人末端法兰的角速度变化曲线，图11 是捞渣机器人末端法兰的角加速度变化曲线。从速度和角速度变化曲线图中分析得出，在机器人的仿真运行过程中，机器人的末端法兰运行平稳，没有出现突变的情况，满足实际的工作需求。

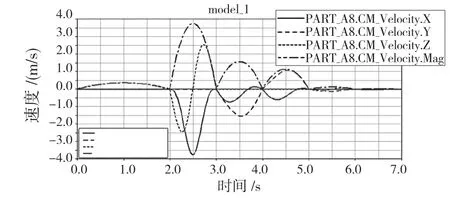
图8 捞渣机器人末端法兰的速度变化曲线Fig.8 Speed change curve of end flange of slag removing robot

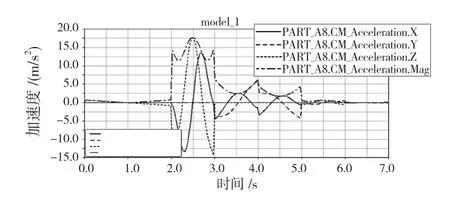
图9 捞渣机器人末端法兰的加速度变化曲线Fig.9 Acceleration variation curve of end flange of slag removing robot

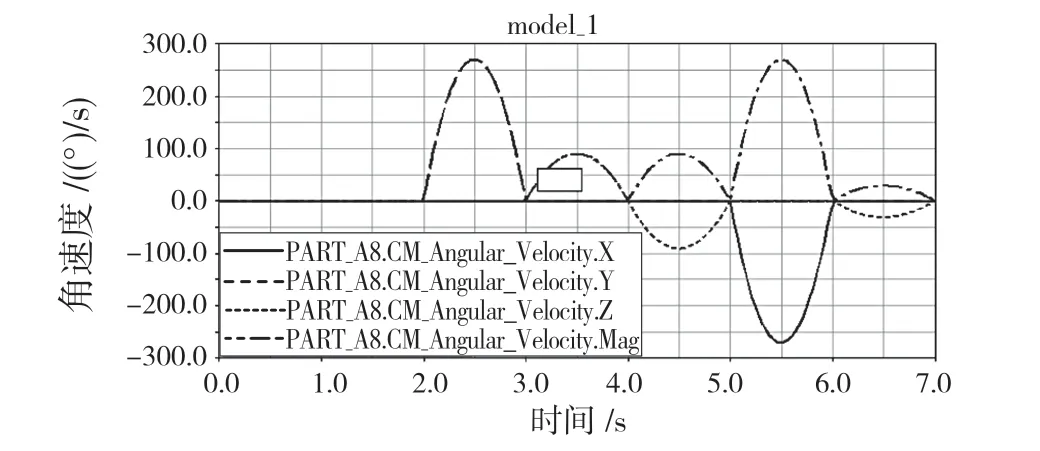
图10 捞渣机器人末端法兰的角速度变化曲线Fig.10 Angular speed change curve of end flange of slag removal robot

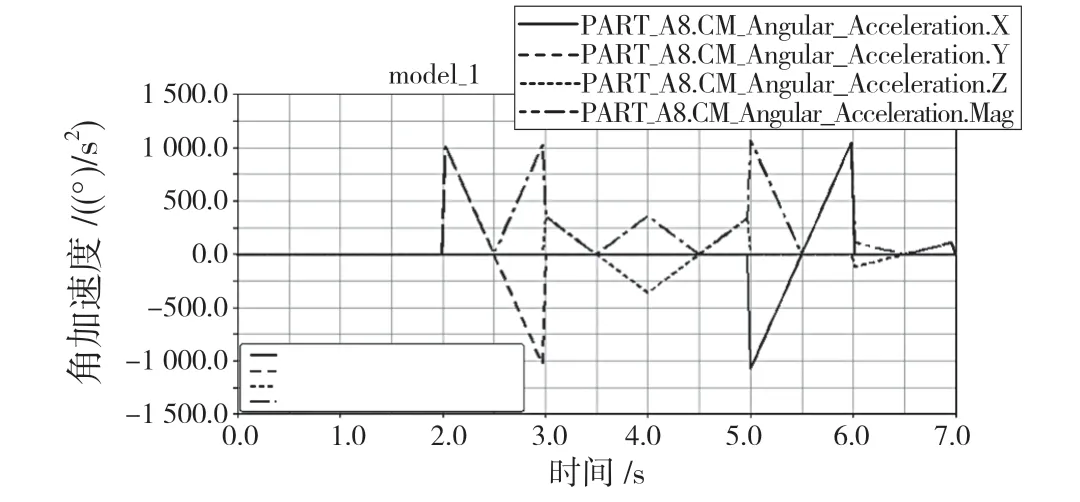
图11 捞渣机器人末端法兰的角加速度变化曲线Fig.11 Angular acceleration curve of end flange of slag removing robot

从加速度和角加速度曲线图中分析得出，机器人在正常运动时加速度变化都比较平稳，但在末端法兰刚启动以及停止过程中出现角加速度突变，由0 变到一个较大数值，这是由不稳定受力造成的，重力、负载等会对加速度产生影响。在中间运行阶段，受力稳定后，加速度变化也趋向稳定。为了避免机器人末端执行器在运行中的不平稳，可以考虑同时对每一个关节进行驱动，这样能够减缓因为多个关节相继驱动而引起的加速度突变，同时还可以提高机器人的动作速度。

4 结语

为了提高捞取锌渣的效率，降低工人的工作强度，设计了一种串联式的捞渣机器人，对其进行了运动学分析。将三维模型导入ADAMS 软件，通过施加约束和添加驱动，得出捞渣机器人末端法兰的位移、速度、加速度等变化曲线图，综合分析可以得出，在本文所规划的轨迹中，机器人末端执行器的位移、速度、加速度随时间都是连续平稳变化的，运行过程中没有发生较大的冲击，运行相对平稳，可以满足实际工作中的任务要求。