基于单调系统理论的光伏并网系统暂态电压稳定性分析
王 波,朱晓杰,李振垚,甘德强,廖圣文,贺 旭
(1. 国网浙江省电力有限公司宁波供电公司,浙江省宁波市 315000;2. 浙江大学电气工程学院,浙江省杭州市 310027)
0 引言
传统电力系统电压稳定问题包括静态电压问题和动态电压问题[1]。其中,静态电压问题一般都是基于潮流代数方程来研究灵敏度[2]或电压解的存在性[3],并根据短路比指标判断电网电压支撑强度[4];在动态电压问题方面,时域仿真仍然是最有效的方法。与以同步发电机为主的传统电力系统相比,高渗透新能源电力系统的动态特性更加复杂,特别是在一次能源特性、组件数量类型和时间尺度等方面存在显著差异。在从传统电力系统向高渗透新能源的现代电力系统过渡阶段,各种动态特性相互影响,动态过程尤为复杂。由于大部分风电、光伏等新能源机组无功功率调节能力不足,电压稳定问题已经成为电力系统安全运行的最大威胁之一。为了更好地理解电力系统电压稳定性的本质,亟须开发更有效的方法和理论。
目前,新能源并网系统的电压稳定性已经得到了深入研究。文献[5]提出了一种考虑新能源接入的全局灵敏度分析方法,与局部敏感性分析相比,全局敏感性分析方法更加准确,计算效率也有所提高。文献[6]利用光伏系统的动态电压支撑能力,使用有功无功注入来提高短期电压稳定性,并缓解了故障后的频率下降程度。文献[7]分析了虚拟同步发电机并联系统的暂态电压失稳机理,并认为恒电压控制模式具有较强的暂态电压稳定性。文献[8]基于小扰动电压稳定性与系统雅可比矩阵奇异性之间的关系,分析了非同步电源对系统电压稳定性的影响。文献[9]提出了新能源并网系统短路比指标,对新能源并网系统的电压支撑强度进行了评估。文献[10]通过奇异值分解重构后的系统潮流矩阵跟踪电压崩溃临界点,进而作为新增新能源机组的指标。
新能源发电机组需要通过变流器连接到电网,根据控制方式不同主要分为跟网性变流器(gridfollowing converter,GFL)和构网型变流器(gridforming converter,GFM)。GFL 通过改变注入电流来控制输出的有功功率和无功功率,其外特性表现为可控电流源。GFM 的结构与GFL 相似,只是在控制结构中去掉了锁相环,并加入了虚拟惯量来模拟同步发电机的摇摆方程[11]。因此,GFM 的外特性类似于可控电压源,在系统发生扰动时可以改变输出功率,直接参与电网的电压和频率控制。部分学者认为GFM 具有电压支撑能力进而可以直接接入无源电网[12]。
单调系统理论作为一种动态系统分析方法,在生物学等其他学科已经发挥了重要作用[13]。国内也有学者对传统电力系统的电压动态特征进行了初步分析,论证了传统电力系统的电压动态模型是混合单调系统[14],并基于单调系统理论为传统电网控制设计提供了理论支撑[15]。为进一步探究新能源发电机组参与电网电压调节的工作原理及稳定机理,本文基于单调动态系统理论对采用不同变流器作为接口的光伏并网系统进行了分析。仿真算例结果验证了本文理论的正确性和有效性。
1 理论基础
1.1 单调系统理论
本节给出涉及的单调系统定义和单调系统互联小增益定理,详细内容见文献[16-18]。
定义1:对于一个如下非线性控制系统ϕ,

式中:z∈Rn为状态向量;v∈Rm为输入向量;f为连续可微映射并满足局部李普希兹条件。
若t≥0 满足下列条件:

式中:v1和v2为2 组输入向量;ξ1和ξ2为2 组初值;-≻为表示向量偏序关系的符号;ϕ(ξ1)和ϕ(ξ2)分别为初始值z1(0)=ξ1和z2(0)=ξ2的解。则称ϕ为单调系统。
定义2:对于带有输出的单调非线性受控系统,则原系统为输入输出单调系统。

定理1(互联单调系统小增益定理):对于2 个互联的输入输出单调系统,

式中:y1、h1、v1、z1和y2、h2、v2、z2分别为2 个互联的输入输出单调系统的输出向量、输出函数、输入向量、状态向量。
当其对应的离散迭代:


收敛至平衡点vˉ1时,则互联系统是全局渐近稳定的,并且,

输入输出单调系统的雅可比矩阵具有以下符号特性,显示了状态变量之间的合作性质和子系统之间的反馈连接特征:

式中:fo、zj、vj、ho分别为向量f、z、v、h中第o个元素和第j个元素。
利用雅可比矩阵的符号特性可以很方便地判断互联系统中子系统的单调性,在子系统都满足单调系统条件时就能采用小增益稳定判据判断互联系统稳定性。
1.2 基于模块化的电网符号特征求取
加入新能源发电机组后电力系统模型更为复杂。为了分析新能源并网系统的稳定性,需要对电力系统网络方程以及状态方程进行解析分析,获取动态系统的符号特征。因此,采用模块化的方式处理相关计算过程,使得系统各变量之间的关系更加清晰。将电力系统动态方程划分为3 个模块部分:
1)元件的动态方程为ż=F(z,Vx,Vy)。其中,向量场F中只包含元件自身的状态变量与端电压变量;Vx和Vy分别为元件端电压在公共坐标轴的x轴和y轴分量。
2)网络方程为YV=Sˉ/Vˉ,等号右端项统一写成功率注入形式。其中,V为节点电压,S为元件注入电网的功率,Sˉ和Vˉ分别为相应变量的共轭;Y为收缩网络方程。
3)元件与网络的接口方程为S=g(z,Vx,Vy),即各元件注入网络的功率。

得到上述各模块的偏导项后,利用链式求导法则可以获得全系统的雅可比矩阵:其中,∂F/∂Vx、∂F/∂Vy和∂F/∂z由元件动态方程直接求得,∂Vx/∂z和∂Vy/∂z通过联立网络方程和接口方程求得,具体步骤如下所示。
结合网络方程和接口方程可得:

式中:diag(∙)为表示由括号内元素组成的对角矩阵的函数;g为g的共轭。
同时,利用如下关系式:

式中:Aˉ、Bˉ、Cˉ分别为A、B、C的共轭。
求解得到:

代入式(9)则可得到系统的雅可比矩阵。
2 暂态电势子系统的符号特征
电力系统暂态过程是功角、频率和电压等多变量变化的复杂过程,难以采用单一分析方法进行稳定性研究,更可靠的方法是将复杂问题进行分解-聚合,对子系统的结构属性进行针对性分析[19]。在研究电力系统电压稳定性时,常关心的是同步发电机暂态电势和励磁系统等子系统,而忽略转子角的变化。因此,推导暂态电势子系统符号特性,并分析不同并网方式的光伏发电单元所带来的变化。
2.1 同步发电机单调性
不计阻尼绕组,励磁系统采用一阶比例模型时,同步发电机暂态电势子系统的动态方程为:
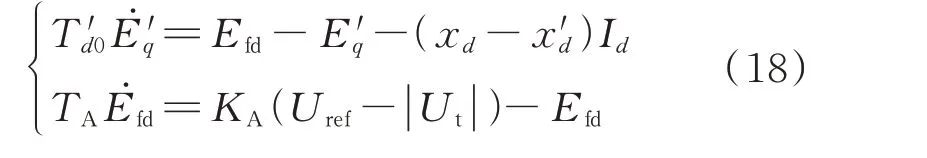
式中:T′d0为开路时间常数;E′q为暂态电抗后的暂态电势;Efd为励磁电压;xd和x′d分别为d轴同步电抗和暂态电抗;TA为励磁时间常数;KA为励磁放大系数;Uref为励磁参考电压;Ut为同步发电机机端电压;Id为定子电流的d轴分量。
结合定子电压方程:

式中:Iq为定子电流的q轴分量;xq为q轴同步电抗;Ud和Uq分别为同步发电机机端电压的d轴和q轴分量;Ux和Uy分别为同步发电机机端电压在系统坐标系中的x轴分量和y轴分量;δ为转子角。
2.1.1 暂态电势的合作性质
根据式(21)求得同步发电机暂态电势动态方程的偏导如下式所示:

根据同步发电机接口方程,即同步发电机注入电网的功率SSM:

将负荷视作恒定阻抗并入网络方程,并利用Kron 变换消去中间节点后,得到式(17)中的A为:

式中:xqi、xdi、Uti分别为第i台同步发电机的q轴同步电抗、d轴同步电抗和机端电压;n为同步发电机节点的数量;Yaug为Kron 变换后的导纳矩阵Y和同步发电机电抗组成的矩阵。
电网导纳矩阵近似为拉普拉斯矩阵,因此,根据Kron 变换性质可知,Yaug近似保持为拉普拉斯矩阵[20]。根据式(15)计算得B和C分别为:

式中:δi为第i台同步发电机的转子角。
根据网络导纳矩阵性质可知,A的元素数量级上百,其共轭逆矩阵元素很小,数量级在10-3到10-2之间。再根据同步发电机参数典型值可以估算B元素的数量级在1 到10 之间,则可以得到近似公式:

式中:Z=-jY-1aug,为阻抗矩阵。
由拉普拉斯矩阵性质可知,Z近似为全正矩阵,并且通过调整参考相位可以使同步发电机q轴相对于参考机角度位于±30°之间,进而使得∂V/∂ΓE'q实部远大于虚部,并且实部均大于0,则

式中:T′d0i和x′di分别为第i台同步发电机的开路时间常数和d轴暂态电抗。
其非对角元素全为正数,满足单调系统条件,说明了同步发电机之间具有合作调压性质。
2.1.2 暂态电势到励磁系统的负反馈
根据式(18)求得励磁系统动态方程的偏导项为:

上述步骤求得同步发电机励磁电压对暂态电势的偏导为:

式中:ΓEfd为由n台同步发电机的励磁电压组成的向量;TAi和KAi分别为第i台同步发电机的励磁时间常数和励磁放大系数。
已知∂V/∂ΓE'q为非负矩阵且实部远大于虚部,Vx通常为正,推导得到励磁电压关于暂态电势的雅可比矩阵为负矩阵。因此,暂态电势是励磁系统的负反馈信号输入。
2.1.3 励磁系统之间的独立解耦
在接口方程中,注入功率不包含励磁电压变量。因此,励磁电压动态方程对励磁电压的偏导矩阵只与∂F/∂z项有关,即:

2.1.4 励磁系统到暂态电势的正反馈
同理,暂态电势动态方程对励磁电压的偏导矩阵只与∂F/∂z项有关,即:

综上所述,当电网中的发电机都为同步发电机时,系统暂态电势子系统的雅可比矩阵具有如图1所示的符号特性。
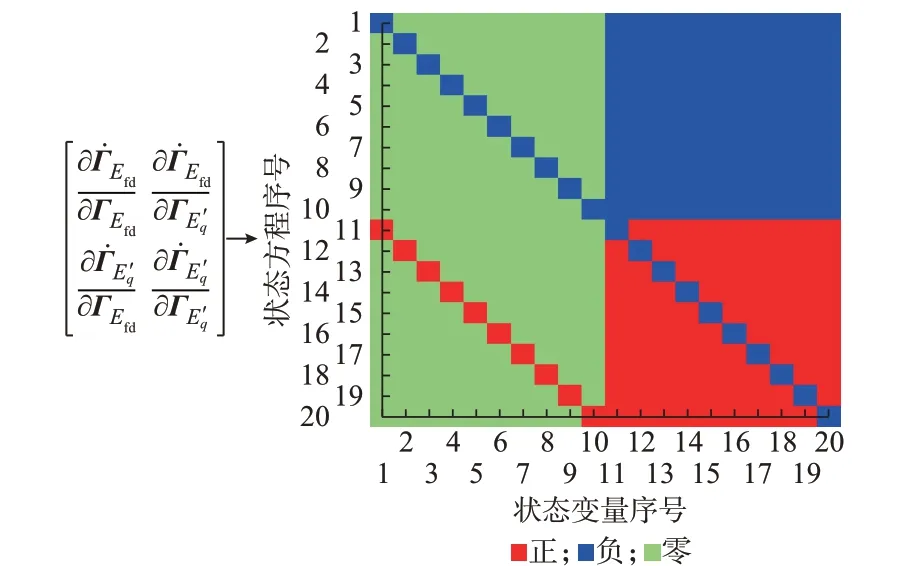
图1 纯同步发电机系统的暂态电势子系统符号特征Fig.1 Sign pattern of transient voltage subsystems of system only with synchronous generators
从上述符号特征可以看出:1)雅可比矩阵的主对角元均为负值,维持电压调节过程的稳定性;2)∂Γ̇E'q/∂ΓE'q和∂Γ̇Efd/∂ΓEfd都满足单调系统条件,说明单调性是暂态电势子系统的固有性质;3)∂Γ̇Efd/∂ΓE'q和∂Γ̇E'q/∂ΓEfd显示2个单调系统之间的反馈连接形式。
根据上述分析可知,雅可比矩阵的符号特性与3 类矩阵的符号特性密切相关,分别为动态方程对电压的偏导∂F/∂V、电压对状态变量的偏导∂V/∂z和动态方程对状态变量的偏导∂F/∂z。将同步发电机相关符号特性总结如表1 所示,并且根据表1 可以推得其他元件的符号特征值。

表1 同步发电机偏导符号特征Table 1 Sign pattern of partial derivatives of synchronous generators
2.2 GFL 符号特征
在机电暂态过程中,通常假设GFL 能够实时跟踪电网频率,因此,忽略锁相环的动力学特性[21]。正常运行时其动态模型可以描述为:

式中:Kpp和Kpi分别为有功功率环节的比例-积分(proportional-integral,PI)控制的放大系数和时间常数;Kqp和Kqi分别为无功功率环节的PI 控制的放大系数和时间常数;Pref,p和Qref,q分别为输出有功功率和无功功率的参考值;PGFL,p和QGFL,q分别为GFL 的输出有功功率和无功功率;zp和zq分别为有功功率和无功功率对应的内部状态变量;IGFL,d和IGFL,q分别为GFL 输出电流的d轴和q轴分量;VGFL为GFL 输出电压。
在研究电压稳定时,往往不考虑有功功率的影响。因此,消去电流变量后得到只有无功功率环节动态方程和接口方程:

式中:VGFL,x和VGFL,y分别为VGFL在系统坐标系中的x轴分量和y轴分量。
从式(37)可以看出,动态方程偏导的符号与光伏发电单元无功功率的流向相关,通常新能源机组运行在单位功率因数控制下,即其无功功率输出为0,此时动态方程偏导项只有∂żq/∂zq不为0。
注意到由GFL 控制的光伏等新能源发电机组无功出力完全由zq控制。因此,电压对无功功率状态变量的偏导矩阵∂V/∂zGFL,q的符号特性与电压对GFL 无功功率的偏导矩阵∂V/∂QGFL相同。其中,QGFL为GFL 无功功率向量,zGFL,q为GFL 无功功率对应的内部状态向量。
将GFL 注入电网的功率表达式SGFL=PGFL,p+jQGFL,q代入接口方程可以求得:

这意味着∂V/∂QGFL近似为全正矩阵,进而∂V/∂zGFL,q也为全正矩阵。利用链式求导法则得到接入GFL 后的系统暂态电势子系统的符号特征如图2 所示。
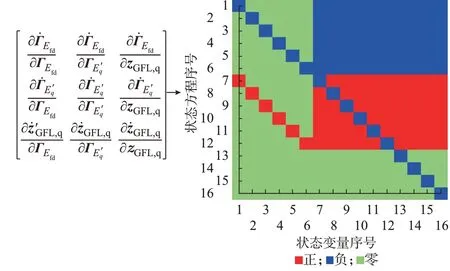
图2 GFL 接入后系统的暂态电势子系统符号特征Fig.2 Sign pattern of transient voltage subsystems of system connected with GFL
综上所述,当GFL 运行在单位功率因数情况时,其自身为单调系统,并且与同步发电机内电势组成的仍然是单调系统,与同步发电机励磁系统之间的反馈也具有类似的规律。因此,可以用互联单调系统小增益定理分析GFL 接入后系统的电压稳定性。
2.3 GFM 符号特征
根据表1 所示的矩阵符号特征可以设计虚拟同步控制使得变流器和同步发电机之间是互联单调系统关系,根据电压源型变流器的电压方程:
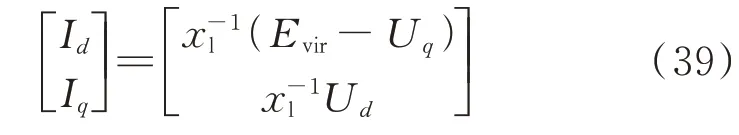
式中:Evir为变流器内部电压;xl为变流器出口阻抗。
可以得到GFM 的输出功率SGFM为:
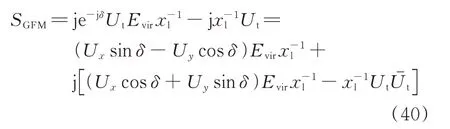
求得GFM 相关的A、B和C矩阵的偏导项如下式所示:
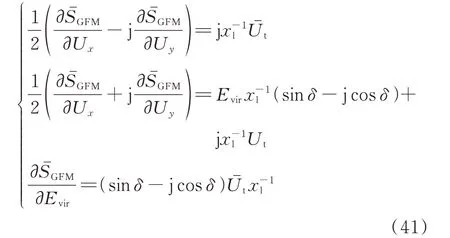
将式(41)与式(24)对比后发现,xl相当于同步发电机暂态电抗,Evir与同步发电机暂态电势有相同的作用。因此,虚拟同步控制下变流器的∂V/∂z符号特征与同步发电机相同,进而设计动态模型方程的符号与同步发电机相同,即可达到两者仍然满足互联单调系统的目的。虚拟同步的无功功率环节输出DV,Q可以用无功功率-电压下垂方程表示:

式中:Kq和Ku分别为下垂系数中的功率系数和电压系数;QGFM为GFM 输送的无功功率;Qref,vir为GFM输送无功功率参考值。
式(42)对电压求导可得:
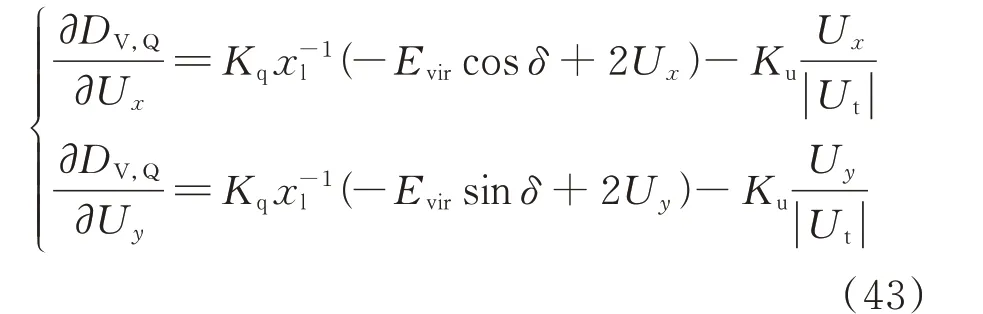
可见,无功功率偏差部分对电压的偏导值基本为正,电压偏差部分对电压的偏导值基本为负。因此,仿照表1,设计虚拟同步控制方式的GFM 数学模型:
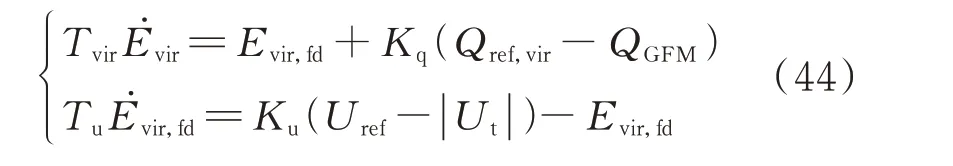
式中:Tvir和Tu为时间常数;Evir,fd为虚拟励磁电压。
GFM 动态方程各项偏导如下所示:

上述式子表明GFM 与同步发电机动态方程偏导符号特性相同,结合∂V/∂z符号特征可知,GFM的雅可比矩阵符号特征与同步发电机完全一致。
至此,本文推导了电力系统暂态电势子系统的雅可比矩阵符号特征,证明了光伏发电单元无论是以何种形式并入电网,都可以与同步发电机组成互联单调系统的形式,进而开展基于互联单调系统小增益定理的电压稳定分析。
3 基于小增益定理的电压稳定分析
3.1 互联系统小增益稳定判据
在得到电力系统暂态电势子系统的雅可比矩阵符号特征后,根据互联单调系统定义可以将其分为2 个单调系统的反馈连接,统称为内电势系统Γ̇E=[ΓE'q,zGFL,q,Evir]和励磁电压系统ΓEf=[ΓEfd,ΓEvir,fd],将 雅 可 比 矩 阵 分 为4 部 分(∂Γ̇E/∂ΓE、∂Γ̇E/∂ΓEf、∂Γ̇Ef/∂ΓEf和∂Γ̇Ef/∂ΓE)。
上述2 个单调系统的反馈连接可以写为如下形式:
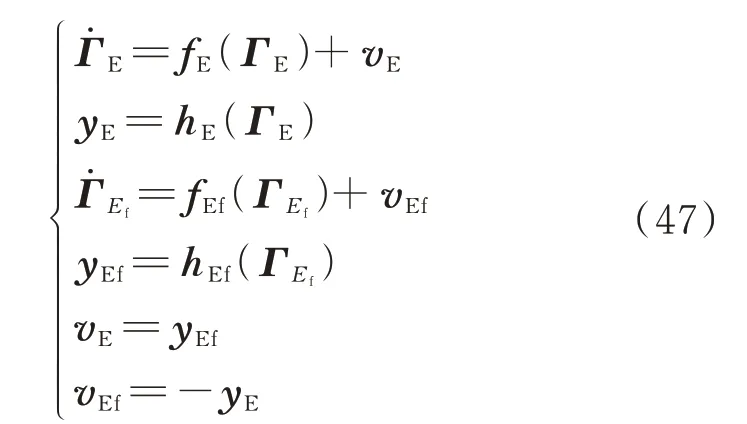
式中:fE、fEf、hE、hEf分别为内电势系统和励磁电压系统的非线性方程;yE、yEf和vE、vEf分别为内电势系统和励磁电压系统的输出向量和输入向量。
系统稳态输入-输出特性为:

式中:G(v)为增益函数。
因此,基于互联单调系统小增益定理,所提出的电压稳定判据为:增益函数的雅可比矩阵的谱半径ρ(∂G/∂v)绝对值小于1,则在不动点vˉt的一个邻域内,vˉt是离散迭代的一个吸引点[22],此时,电力系统是电压稳定的;若谱半径绝对值大于等于1,则离散迭代可能不收敛,表示电力系统存在电压失稳的风险。
3.2 参数稳定分析
增益函数的雅可比矩阵∂G/∂v表达如下:

对比式(47)和元件动态方程可以得到以下对应关系:
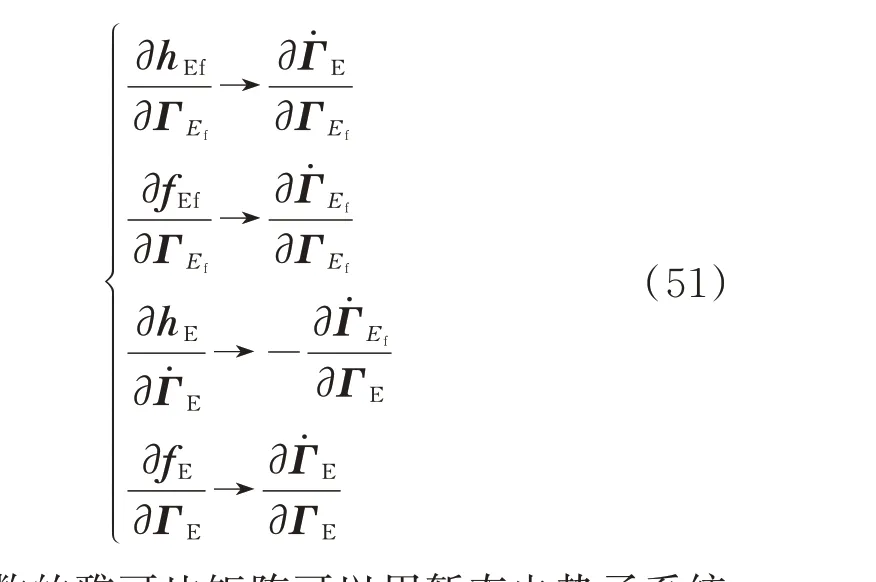
增益函数的雅可比矩阵可以用暂态电势子系统的雅可比矩阵来表示。其中,∂Γ̇E/∂ΓEf和∂Γ̇Ef/∂ΓE显然为非负矩阵,∂Γ̇Ef/∂ΓEf和∂Γ̇E/∂ΓE的逆也为非负矩阵。因此,可以基于非负矩阵理论对雅可比矩阵谱半径进行分析。
对于非负矩阵NA≥0,当0 ≤NA-NB时认为NA≤NB,并且非负矩阵具有以下性质[23]:
1)设NA、NB、NC、ND为非 负矩阵,若0 ≤NA≤NB,0 ≤NC≤ND,则0 ≤NANC≤NBND。
2)设NA、NB为 非 负 矩 阵,若NA≤NB,则ρ(NA)≤ρ(NB),其中ρ(∙)为矩阵的谱半径。
由非负矩阵性质可推导出,雅可比矩阵元素绝对值增加会使得∂G/∂v元素绝对值增加,最终导致ρ(∂G/∂v)绝对值大于1,也就不能保证离散迭代系统的收敛,对应着系统稳定性变差。
从雅可比矩阵的解析表达式可以分析系统参数对稳定性的影响:
1)同步发电机参数稳定分析。从式(32)可以看出暂态电抗的减小和励磁放大系数的增大都会增加∂hE/∂ΓE的绝对值,进而导致增益函数的雅可比矩阵谱半径增加,恶化了暂态电势子系统的稳定性。
2)GFL 影 响 分 析。从 图2 可 以 看 出,GFL 替 换同步发电机后,系统阶次降低,剩余同步发电机对系统的稳定性影响变大,导致系统鲁棒性变差。
3)GFM 参数稳定分析。从式(45)可以看出虚拟同步控制方式中,参数Kq越大,∂Γ̇E/∂ΓE的对角元素越大,因此,其逆矩阵元素越小,增益函数的雅可比矩阵谱半径越小;参数Ku越大,∂Γ̇Ef/∂ΓE元素越大,增益函数的雅可比矩阵谱半径越大。因此,理论上在合理范围内,虚拟同步控制方式的无功功率-电压下垂系数(Kq与Ku的比值)越大,电力系统的电压稳定性越好。同理,变流器出口阻抗xl越大,增益函数的雅可比矩阵谱半径越大,电力系统的电压稳定性越差。
综上所述,基于小增益稳定判据可以采取以下措施提高系统电压稳定性:1)减小同步发电机励磁系统放大系数KA;2)光伏发电单元采用GFM 方式并网;3)提高GFM 虚拟同步控制方式的无功功率-电压下垂系数;4)减小变流器出口阻抗xl。
4 算例分析
本文在MATLAB/Simulink 仿真平台中,采用10 机39 节点系统算例对上述结论的正确性和有效性进行验证,其他算例可以得到相同的结论。将采用以下3 种案例进行分析:
案例1:发电机组全为同步发电机,同步发电机参数如附录A 表A1 所示。
案例2:将1 至4 号同步发电机替换为GFL 为接口的光伏发电单元,GFL 参数如附录A 表A2 所示。
案例3:将1 至4 号同步发电机替换为GFM 为接口的光伏发电单元,GFM 参数如附录A 表A3所示。
4.1 纯同步发电机系统的参数稳定分析
在案例1 中研究纯同步发电机系统的雅可比矩阵符号特性。为确保在系统动态过程中,暂态电势子系统保持着互联单调系统性质,在t=0 s 时刻设置三相短路故障,0.06 s 后清除故障,整个动态过程中雅可比矩阵符号变化均符合图1 的互联单调系统符号特征,证明单调性是暂态电势子系统的内在固有特征,运用单调系统理论能够有效分析电力系统的电压稳定性。
为研究参数对系统电压稳定性的影响,逐步增加5 号同步发电机的励磁放大系数和暂态电抗,计算增益函数的雅可比矩阵谱半径随参数变化的趋势,结果如图3 所示。

图3 同步发电机参数对谱半径的影响Fig.3 Influence of parameters of synchronous generators on spectral radius
从图3 可以看出,随着同步发电机暂态电抗的减小和励磁系统放大系数的增加,增益函数的雅可比矩阵谱半径不断增加,这意味着暂态电势子系统平衡点的渐进稳定性受到破坏,电力系统更易出现电压失稳问题。而传统的电压稳定分析方法,如基于电压-无功功率灵敏度的电压稳定分析方法[24],其建立在潮流方程基础上,通过节点的无功功率-电压灵敏度判断系统电压薄弱点,但是其方程不包含电力系统动态方程,因此无法反映参数稳定问题。
4.2 GFL 接入对谱半径的影响
在案例2 中不考虑光伏发电单元低电压穿越的过程,只计算短路清除后系统的自治恢复过程,整个动态过程中雅可比矩阵符号变化均符合图2 的互联单调系统符号特征。
为验证GFL 替换同步发电机后,剩余同步发电机对系统稳定性的影响,分别计算案例1 和案例2中谱半径对5 号同步发电机暂态电抗和励磁系统放大系数的灵敏度,结果如表2 所示。

表2 谱半径对同步发电机参数的灵敏度Table 2 Sensitivity of spectral radius to parameters of synchronous generators
从表2 可看出,在案例2 中,谱半径对同步发电机参数的灵敏度比案例1 大,这说明同步发电机被替换为GFL 后,谱半径更易受剩余同步发电机参数影响,暂态电势子系统的鲁棒性变差。
4.3 GFM 参数稳定分析
在案例3 中设置三相短路故障,整个动态过程雅可比矩阵符号变化均符合图1 的符号特征,证明GFM 能够模拟同步发电机的调压性质,并保持互联单调系统特性。
为分析GFM 参数对系统电压稳定的影响,分别逐步增加GFM 的无功功率-电压下垂系数(Kq与Ku的比值)和出口电抗xl,计算增益函数的雅可比矩阵谱半径随参数变化的趋势,结果如图4 所示。

图 4 GFM 参数对谱半径的影响Fig.4 Influence of parameters of GFM on spectral radius
从图4(a)可以看出,随着无功功率-电压下垂系数的增大,谱半径逐渐减小,但在曲线后半段谱半径减小的速度开始平缓。这说明过大的下垂系数在电网电压跌落时不仅使得GFM 更加接近极限输出功率,对GFM 自身稳定性造成影响,对电压稳定性的提升也不明显。因此,选择合适的无功功率-电压下垂系数有利于协调GFM 自身和整体电网的稳定性需求。
出口电抗xl决定了新能源与电网之间的连接强度,从图4(b)可以看出,随着出口电抗xl的增大,谱半径逐渐增大,根据小增益稳定判据可知,减小变流器出口电抗有利于增强电力系统的电压稳定性。
5 结语
单调动态系统理论的出现为理解混联电网的协调电压控制提供了一个契机,利用电力系统机电暂态模型固有数学特征,结合特殊矩阵论,单调动态系统理论能够阐明发电机组之间的无功电压支撑合作关系。发电机组控制参数与动态响应间的单调关系,也是单调动态理论旨在揭示的现象之一,有利于光伏并网系统协调控制设计的进一步实施。本文基于互联单调系统理论,对采用不同变流器作为接口的光伏并网系统进行了分析,并得出以下结论:
1)在机电暂态过程中,同步发电机的暂态电势和励磁系统两者自身都是单调系统,并通过正/负反馈连接,形成互联单调系统。同步发电机暂态电抗的减小和励磁系统放大系数的增大会增加增益函数的雅可比矩阵谱半径大小,从而不利于电力系统的电压稳定性。
2)电网中的同步发电机被替换为GFL 后,谱半径对剩余同步发电机参数的灵敏度增大。这也说明由于GFL 不参与电网的电压调节,剩余同步发电机需要在电网电压波动时承担更多的功率负担,使得系统鲁棒性变差。
3)采用虚拟同步控制方式的GFM 能够模拟同步发电机的电压调节功能,其动态方程与同步发电机具有相同的符号特征。无功功率-电压下垂系数反映了GFM 参与电网调压时的作用,通过小增益稳定判据发现,在考虑电力电子器件自身的安全性和稳定性的同时,较大的无功功率-电压下垂系数能够提高电网的电压稳定性。同时,较小的变流器出口电抗有利于增强电力系统的电压稳定性。
本文从电力系统电压动态角度出发,分析了光伏发电单元对电网电压单调动态特征的影响。在该过程中,对同步发电机功角动态和光伏发电单元有功动态等环节进行了一定程度的简化。因此,下一步将对电网有功功率响应特征进行分析,厘清电压稳定与功角稳定之间的耦合交互关系,为后续分析电网稳定性提供理论基础。
本文工作受国网浙江省电力有限公司科技项目(高比例光伏接入受端电网电压动态解析分析,5211NB200138)资助,谨此感谢!
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

