基于遗传算法的隧道-坡体耦合稳定性分析

林贵超LIN Gui-chao

（龙岩市永定区建设工程质量安全站，龙岩 364105）

0 引言

隧道轴线与坡面走向一致时，隧道在较长区段的覆盖层较薄，容易出现偏压，应尽量避免。但在实际工程中受地形限制仍不可避免出现这种情况，此时，需要将隧道-边坡作为整体进行分析。

目前，国内外工程实践中广泛采用的极限平衡法、滑移线法、有限元法、数学规划法以及智能方法等边坡稳定性分析方法都得到了较大的发展。如日本的Marbusa 提出了边坡稳定分析的复合算法，采用极限平衡方法进行稳定性分析同时再利用有限元对边坡的应力、应变进行计算，并通过工程验证了其有效性。Zienkiewiec 在进行边坡稳定分析时引入强度折减技术，Kumar 进行边坡稳定分析引入序贯无约束极小方法，都很好地解决了当前的工程实际问题，得到有效验证，也得出了有意义的结论，为后续科研人员的研究工作提供帮助。

国内学者高峰等以沙湾大断面隧道为研究背景，应用ANSYS 对双侧壁导坑法施工的隧道进行了稳定性分析；张秀丽等用改进的非连续变形分析（DDA）方法，对某公路隧道进行了稳定性分析；马宗源等建立了双剪统一弹塑性本构模型的显式有限差分格式，对陕西省泾阳县南塬高边坡进行了滑坡规模和滑坡前后的地形特征分析；王艳霞等利用模糊理论的思想介入边坡稳定研究，针对边坡稳定自身的特点利用模糊数学的方法进行分析，获得一定的成果。

由此可见，极限平衡法是边坡工程设计和稳定性分析的有效方法，但对于原始边坡、隧道和路堤边坡三者耦合分析的成果不多，本文采用Janbu 条分法，建立了原始边坡-隧道-路堤边坡三者耦合的稳定性计算模型，基于遗传算法原理，运用MATLAB 数学工具二次开发功能进行了编程，对不同工况下原始边坡-隧道-路堤边坡三者耦合坡体的稳定性进行分析。

1 隧道-坡体耦合稳定性计算模型

隧道洞口边坡破坏多为圆弧形滑面，由于Janbu 法适用于任何滑面的边坡稳定性分析，所以，本文以垂直于隧道轴线的典型断面为研究对象，选用简化Janbu 法并以假设滑面为圆弧形滑面进行分析，如图1 所示。

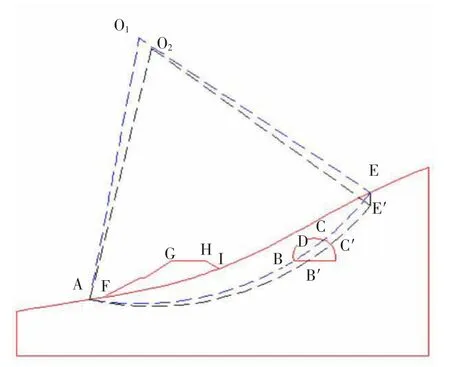
图1 隧道进口段坡体分析模型

图2 为潜在滑块的某一分析土条，条块上作用力有分块的重量Wi；条间作用力的水平分力Xi；条间作用力的垂直力Yi；条块底面的抗剪力（抗滑力）Ti；条块底面的法向力Ni。

图2 简化Janbu 法计算简图

根据垂直方向力平衡∑Y=0，得：

由库仑破坏准则可得：

联立式（1）、式（2）和式（3），可得：

由简化的Janbu 法假定可知Yi-Yi+1=0，则变为：

式中，Fs为安全系数；li为分块滑面长度（li≈bi/cosαi）；bi为岩土条分块宽度；αi为分块滑面相于水平面的夹角；ci为滑体分块滑动面上的粘结力；φi为滑面岩土的内摩擦角；i 为分析条块序数；n 为分条数。

因为nai中也有Fs，可先假定Fs等于1，进行试算：假如Fs≠1，那么用公式（8）计算获得新的nai及Fs值，依次循环迭代，至Fs趋于稳定为止。工程实践表明，迭代计算收敛的前提下，一般3 至4 次的迭代计算结果可以有效满足工程要求。

这样计算即可以得出不同工况下的坡体稳定性安全系数。该系数是针对某假定潜在滑动面求得的，在计算分析时往往要求出最小安全系数及其对应的潜在滑动面。

2 坡体稳定性遗传算法计算设计

2.1 算法设计

传统优化方法相比较于遗传算法针对简单边坡滑面搜索时有很高的效率，但对于多级边坡工况和土层复杂的边坡时，却很难得到全局最优解，搜索很容易陷入局部极小值。遗传算法则可以弥补上述不足。坡体稳定性遗传算法计算主要包括设计变量、安全系数表达式和适应度函数设计三部分。

2.1.1 设计变量

本文以飞机部件交点装配协调为研究对象，在建立特征公差域与T-Map映射关系的基础上，提出了基于T-Map的部件交点装配数字化协调方法。

设计变量：①滑弧的圆心坐标（X0，Y0）；②滑弧半径R（或滑动深度R-Y0），如图3 所示。这样设计虽然圆心坐标的可行解搜索区域及半径相对较难确定，但是可以直观地直接得到滑弧位置。同时，在实际工程中，当边坡表面的形状不规则时，采用传统的方法将使求解圆弧滑裂面与边坡面的左右交点（l 和r 交点）变得极为复杂和困难。改用圆弧滑裂面与边坡的左右交点的和圆心的三个X 坐标作为设计变量，将可使每个控制几何参数的确定变得简单明了。

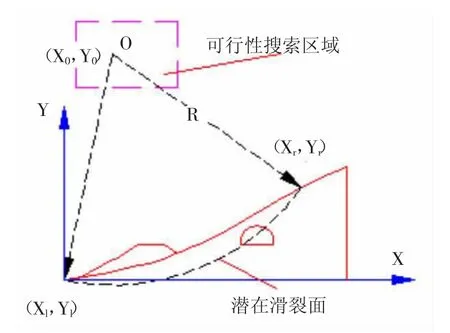
图3 遗传算法设计变量分析图

首先确定Xl和Xr，然后，由边坡表面形状分布函数求得Yl和Yr，即圆弧滑裂面与坡面的交点，最后，根据如图4所示的潜在滑裂面几何关系，推导出Y0和R 的计算公式如下：

图4 坡体稳定性计算表达式分析图

式中：Ω 为三维欧式空间R3的一个子域。

2.1.2 安全系数表达式推导

边坡稳定性计算模型坐标系如图4 所示。从潜在滑体内取出任一单位厚度的微分土条，土条宽度为dx，作用在该微分土条上的诸力如图1 所示，y1为坡面线函数方程，y2为潜在滑动面函数方程。

由图3 中可以得出：

由公式（12）至（15），即可以推导出不同工况下边坡稳定性安全系数积分表达式。

2.1.3 适应度函数的设计

对于坡体最危险滑动面搜索问题，其目标函数为坡体安全系数Fs，由设计变量所确定的每一个潜在滑动面都对应着一个安全系数Fs，所以Fs是X 的函数，即。由于该问题是求目标函数的最小值，且适应度函数要求非负，所以可将适应度函数定义为：

该目标函数为隧道进口段坡体稳定分析模型不同施工阶段的计算表达式。

在完成变量设计、遗传编码、目标函数及适应度函数设计、并确定计算方法之后，就可以将对于坡体最危险滑动面搜索问题作为以下非线性函数优化问题进行计算：

2.2 算法实现

边坡最危险滑动面搜索是一个以安全系数Fs作为最小化目标函数，以滑动面位置和形状控制参数作为状态变量的最优化问题。运用遗传算法求解这一问题，必须要将该问题表述为适合于遗传算法求解的模式。即要确定该问题的解（个体）的编码、初始种群、适应度函数和各种遗传操作方式，具体流程如图5 所示。本文运用MATLAB 数学工具对其进行二次开发实现基于遗传算法坡体稳定性计算。

图5 遗传算法计算流程框图

3 结论

①基于极限平衡Janbu 条分法，建立了原始边坡-隧道-路堤边坡三者耦合坡体稳定性分析模型。②应用遗传算法，进行了原始边坡-隧道-路堤边坡三者耦合坡体的计算变量、安全系数积分表达式、适应度函数设计。③原始坡体随着隧道开挖承载力下降，随路堤修筑荷载增加，坡体安全系数逐渐降低，路堤修筑后安全系数为1.38 大于规范规定的1.3，坡体趋于稳定。