小流量工况泵阀耦合系统失稳机理研究
于 涛,率志君,王 曦,简 洁,李玩幽,姜晨醒,肖 颀
(1. 哈尔滨工程大学 动力与能源工程学院,哈尔滨 150000;2. 厦门大学 能源学院,福建 厦门 361000;3. 武汉第二船舶设计研究所 热能动力技术重点实验室,武汉 430205)
泵阀耦合系统的稳定性对于核电站给水系统的安全运行至关重要。离心泵、弹簧阀以及管路等部件是核电站给水系统的重要组成部分,各元件协同作用,保证系统正常运行。弹簧止回阀安装在离心泵出口处,阀门开度根据不同工况下的流量和压力等参数进行自我调节,使得泵阀耦合系统能够适应多种运行工况,并表现出良好的特性[1]。核电站系统的安全设计至关重要,其中稳定可靠的回路系统是保证核电系统平稳运行的重要组成部分,因此对低振动的泵阀耦合子系统提出了更高要求。
根据系统运行需要,泵阀耦合系统往往需要在小流量工况条件下运行,容易引起系统的流动失稳。一方面,离心泵流场内部会发生失速现象,从而诱发幅值较高的低频压力脉动,使得离心泵振动加剧[2-9]。周佩剑等[10]研究了小流量工况下离心泵隔舌区域的流场特性,发现失速团常出现在逆压梯度较大的区域,造成流道堵塞,引发高幅值压力脉动。瞿丽霞等[11]研究了双吸离心泵的流场特性,发现偏离额定流量程度越大,叶轮内部的压力脉动幅值越高。Sano等[12]采用油膜法显示技术捕捉到了离心泵导叶中的失速现象,并研究了导叶失速所引起的低频压力脉动。另一方面,当离心泵下游使用受系统参数实时调节的被动式弹簧阀时,阀内流动特性和阀瓣瞬态动力学特性受上游压力波动影响很大,可能导致阀瓣颤振,甚至出现敲击现象,严重影响泵阀耦合系统的可靠性[13-17]。张伟涛[18]和刘华坪等[19]研究了阀门在开启和关闭过程中的阀瓣受力特性以及逆流冲击的产生原因。Botros[20]研究了止回阀的动态过程,发现当水动力小于弹簧力时,阀门不能全开,阀体振动加剧。Qian等[21]研究了不同进口压力下阀瓣运动规律以及阀瓣受力情况,发现进口波动压力对阀瓣受力影响很大,并且研究了阀内弹簧刚度对开阀过程的影响。
目前对于泵阀耦合系统流致激励特性的研究,更多关注于固定阀门开度或阀门开度变化规律已知的情况[22-26]。张玉良等[27-28]建立了离心泵的循环管路系统,研究了启动过程中的外特性和内部流动演化特性。杨帅[29]采用MOC-CFD耦合模拟,研究了快速开阀和关阀过程中泵的动态特性和瞬态流动的演化过程。刘巧玲[30]采用一维与三维耦合计算,研究了不同启动方式下并联泵送系统瞬态特性。对于使用受离心泵出口压力实时调节的被动式弹簧阀的研究仍是较少。因此研究小流量工况泵阀耦合系统的流场特性以及结构动力学特性具有重要的科研价值。本文以某泵阀耦合系统为对象,重点研究小流量工况非稳态流致激励特性,并阐明泵阀耦合系统颤振现象的产生机理。
1 计算区域及方法
1.1 弹簧止回阀工作原理
本文所研究的弹簧止回阀是由一个进口和两个出口所组成的三通结构。弹簧止回阀的阀门开度受到流体介质的压力,阀瓣的重力和弹簧的阻力等共同作用。当入口压力小于阀瓣的触发压力时,流体通过阀杆底部进入阀杆内部,随后经由空排口流出阀门;当入口压力达到阀瓣触发压力,阀门完全打开,阀杆随着阀瓣向上运动,流体介质无法通过阀杆流向空排口,而只能由主出口排出。由图1阀瓣受力分析可知,阀瓣运动过程是在压差引起的流体力、运动部件重力和弹簧力的平衡过程中实现的,根据牛顿第二定律总结出阀瓣运动方程如式(1)所示。
(1)
式中:m为运动部件质量;k为弹簧刚度;F为阀瓣所受流体力;c为阻尼;x0为弹簧的初始位移。

图1 阀瓣受力分析Fig.1 Valve force analysis
1.2 计算区域
本文的研究的泵阀耦合系统是一个复杂的多部件耦合系统,离心泵和弹簧止回阀是系统中两个主要的运动设备。泵出口流体介质推动弹簧止回阀阀瓣运动,是阀瓣所受流体激励的主要来源,离心泵出口压力变化和流量波动情况将直接影响阀门内部流场特性。泵阀耦合系统的几何和性能参数由表1给出。针对离心泵计算,旋转区域叶轮要单独进行设置,因而将离心泵的流体域分成四部分:入口导叶、叶轮、出口导叶以及蜗壳。对于弹簧止回阀计算,需要将阀瓣壁面和阀杆设置为刚体运动,并赋予一定的运动规律,进而模拟阀瓣的运动过程,因此将弹簧止回阀的流体域分成三部分:阀体、阀杆以及空排口。离心泵和弹簧止回阀的流体区域如图2所示。

表1 主要参数Tab.1 Main parameters

图2 主要部件流体模型Fig.2 Fluid model of main components
试验中系统通过主出口的闸阀控制回路流量,仿真中将其简化为具有缩扩结构的管路,无需施加流量边界条件而自耦合求解,流量参数变化通过内部计算获得。通过减小阀门喉部直径来增大局部水力损失,进而减弱过流能力,通过调节阀门喉部直径即可获得相应的稳定流量和系统阻力。通过试验数据分析发现,当总流量小于0.14倍额定流量时,阀门处于关闭状态,流体只能通过空排口排出;当总流量大于0.4倍额定流量时,阀门完全打开,流体只能通过主出口排出;当泵阀耦合系统在0.14~0.4倍额定流量之内运行时,阀门处于半开半闭状态,流体既能通过主出口排出又能通过空排口排出,且开度越小,阀瓣处的流动越复杂,受离心泵出口压力脉动的影响较大。根据系统运行需要,0.2倍额定流量为典型工况点,更容易引起系统流动失稳,所以本文选取该流量点进行研究。为了更真实的模拟流场内部流动,对泵阀耦合系统进出口流域做相应延长,以便其在边界处的流动能够充分发展。本文采用四面体单元对流体区域进行网格划分,计算区域网格如图3所示。

图3 计算区域网格Fig.3 Computational domain mesh
1.3 计算方法
本文使用ANSYS FLUENT软件对计算域的控制方程进行求解,并采用RNGk~ε湍流模型封闭方程组[31],其主要特点是考虑了高波数、小尺度涡对低波数、大尺度涡的影响,提高了漩涡流动的精度,在求解离心泵和阀门流场方面具有优势[32-35]。进口采取总压边界条件,出口采取静压边界条件,均设置为0.1 MPa。叶轮流域设置为旋转域,转速为2 980 r/min,同时导叶流域与叶轮前后盖板外侧相接触的部分,设置为旋转壁面,其他流体域设置为静止区域。弹簧止回阀的阀瓣运动过程受压差大小以及弹簧位移量实时控制,因此采用UDF宏命令对阀瓣运动方程进行编译,其具体计算流程如图4所示。根据牛顿第二定律求取阀瓣的运动加速度和速度,并将运动速度赋值给阀瓣,进而指定刚体的运动方式。网格更新方法采用Smoothing和Remeshing结合的方式,对网格质量不好的区域进行网格重新划分。

图4 计算流程图Fig.4 Calculation process diagram
在瞬态求解中,采用滑移网格模型来模拟动静干涉效应,叶轮每旋转2度计算一个时间步。在流场计算分析之前,分别对离心泵和弹簧止回阀进行网格无关性以及Yplus值检验。由图5可知,当离心泵和弹簧止回阀的网格数量分别达到160万和190万之后,网格数目继续增长对扬程和阀瓣升力的收敛性贡献很小。因此综合考虑计算精度和时间成本,本文采取350万网格总量的计算模型,各区域网格数为:阀体132.1万、空排口26.7万、阀杆15.8万、入口导叶14.9万、叶轮36.4万、蜗壳导叶99.5万和进出口管路24.6万。所有流域的Yplus值均小于150,满足RNGk~ε湍流模型的适用条件。

图5 模型检验Fig.5 Model checking
1.4 水力特性试验验证
本文试验回路由离心泵、弹簧止回阀、闸阀和管道回路组成,试验装置台如图6所示。离心泵由电机驱动,变频电机转速为2 980 r/min,满足试验要求。
图7(a)和图7(b)为离心泵和弹簧止回阀的外特性曲线,其中流量比为主出口流量和空排口流量的比值。通过对比试验与仿真数据发现,二者基本吻合。图7(c)为离心泵出口压力频域曲线,对比发现离心泵出口压力在叶频248.3 Hz及其倍频和低频3.8 Hz处均存在明显的峰值,仿真结果与试验结果基本一致,仅存在幅值上的区别,主要原因是计算过程中对边界条件的简化。综上所述,数值计算结果可信。

注:1.水箱;2.压力表;3.离心泵;4.压力脉动传感器;5.弹簧止回阀;6.闸阀;7.流量计。图6 试验装置台结构图Fig.6 Test system structure

图7 试验值和仿真值对比Fig.7 Comparison of experimental and simulation results
2 计算结果及分析
2.1 内部流动分析
由图8泵阀耦合系统压力和速度分布图可知,由于离心泵对经其内部流体的增压作用,离心泵流场内部压力沿流动方向压力逐渐增加,并且受动静干涉作用的影响,导叶隔舌处是整个流场内压力变化最剧烈的位置,同时叶轮内压力等值线与叶片表面不再垂直,说明叶片表面处存在着较大压力梯度。当流体流经闸阀和阀杆进出口等过流面积较小的区域时,受节流作用的影响,主出口和空排出口处压力明显降低。流体在经过叶轮做功之后,流速明显升高,在导叶入口处达到最大,并且叶轮和导叶流道存在明显的流动分离、漩涡和回流等不稳定现象。当流体流经狭小的阀瓣间隙和阀杆窗口时,由于过流面积较小,流体被挤压为一股高速射流,这样多股水流相遇对撞以及流动死角的存在所引起的锐缘现象,使得阀门流场内部出现了尺度各异的漩涡结构。
2.2 瞬态流动特性分析
小流量工况下泵阀耦合系统流场内部存在较多的漩涡结构,会对其压力分布特性产生影响。为了探究泵阀耦合系统瞬态流动特性,在流场内部布置压力脉动监测点,如图9所示。

图8 压力与速度分布Fig.8 Distribution of pressure and velocity

图9 监测点分布Fig.9 Distribution of monitoring points
图10为导叶和蜗壳区域监测点压力脉动频域曲线,其主要频率为叶频及其倍频和低频3.8 Hz。离心泵出口压力脉动表现出与蜗壳监测点一样的频率分布特性,主要集中在低频3.8 Hz,其产生原因将在后续进行详细说明。与导叶区域相比,蜗壳区域的压力脉动幅值明显下降,主要是因为流体流入蜗壳后,过流面积突然增大,流体发生强扩散现象,导致压力脉动产生衰减。但是不同频率的压力脉动幅值衰减程度也不一样,叶频及其倍频衰减较大,而低频3.8 Hz衰减较小,这与其产生机理有关。叶频的产生源于动静干涉效应。低频的产生则与导叶区域的周期性堵塞密切相关。导叶失速会引起较大的流量脉动,其引起低频压力脉动相较于叶频不易耗散,因此压力幅值下降幅度较小。
通过前部分的研究可知,导叶流域可能存在产生低频压力脉动的周期性堵塞,进而对离心泵导叶流量进行监测分析。由图11可知,各个导叶流道不断的发生阻塞和退出阻塞并且沿着顺时针方向不断传递,在39个叶轮旋转周期内存在3个明显的失速周期,其中1个叶轮旋转周期为叶轮旋转1周所需要的时间。由于导叶失速团产生时,会阻塞流道进口的大部分面积,导致各个流道内的流量进行重新分配,更多的水流进入到相邻流道,流量也就发生周期性的变化。受导叶区域的周期性堵塞的影响,压力脉动也呈现出周期性变化,1个导叶失速周期所需的时间为0.26 s,体现在频率上为3.8 Hz。
通过不同时刻流线图,可以更加直观的观察到整个失速过程。图12为不同时刻叶轮截面流线图,T为一个叶轮旋转周期,由图可知,随着叶轮旋转,沿着叶轮旋转方向导叶区域会发生周期性的堵塞,并且以13个叶轮旋转周期为一个导叶失速周期。

图10 监测点压力脉动频谱Fig.10 Pressure pulsation spectrum at the monitoring point

图11 导叶流量分布Fig.11 Flow distribution of guide vane
流体对过流结构表面的作用力包括压力和黏性切应力两部分[36]。不过,由于水的黏性比较小,叶轮径向力和阀瓣受力主要以流体压力为主,采用直接积分法,可以直接获取叶轮表面和阀瓣表面上所受到的作用力大小及方向,其计算公式为
(2)
式中:p为作用于表面A的压力;e为表面A的法向量。
由图13叶轮径向力频谱可知,其主要频率为低频3.8 Hz、轴频49.7 Hz和3倍叶频745 Hz,并且在低频3.8 Hz处峰值最高,表明导叶的周期性堵塞也会对其上游部件产生影响。

图12 叶轮截面流线图Fig.12 Streamline diagram of impeller section

图13 叶轮径向力频谱Fig.13 Spectrum of the impeller radial force
2.3 阀瓣瞬态动力学特性
阀瓣运动特性取决于阀瓣所受的流体力、弹簧力和自身惯性力,其中弹簧力和惯性力都是结构属性,而流体力则完全取决于阀内流动特性。阀瓣运动过程是阀瓣所受流体力、阀瓣重力和弹簧反作用力的平衡过程中实现的,并且离心泵的出口压力将直接影响阀瓣所受流体力。由图14(a)可知,在离心泵的运转过程中阀瓣受力始终在正负波动,且存在较为明显的周期性,这将直接决定阀瓣的运动过程,进而引发弹簧止回阀的颤振现象。由图14(b)可知,阀瓣受力在低频3.8 Hz和10.2 Hz存在较高峰值,其中低频3.8 Hz与离心泵出口压力脉动的低频成分相一致,而10.2 Hz则与弹簧止回阀内部的弹簧质量的固有频率相接近。
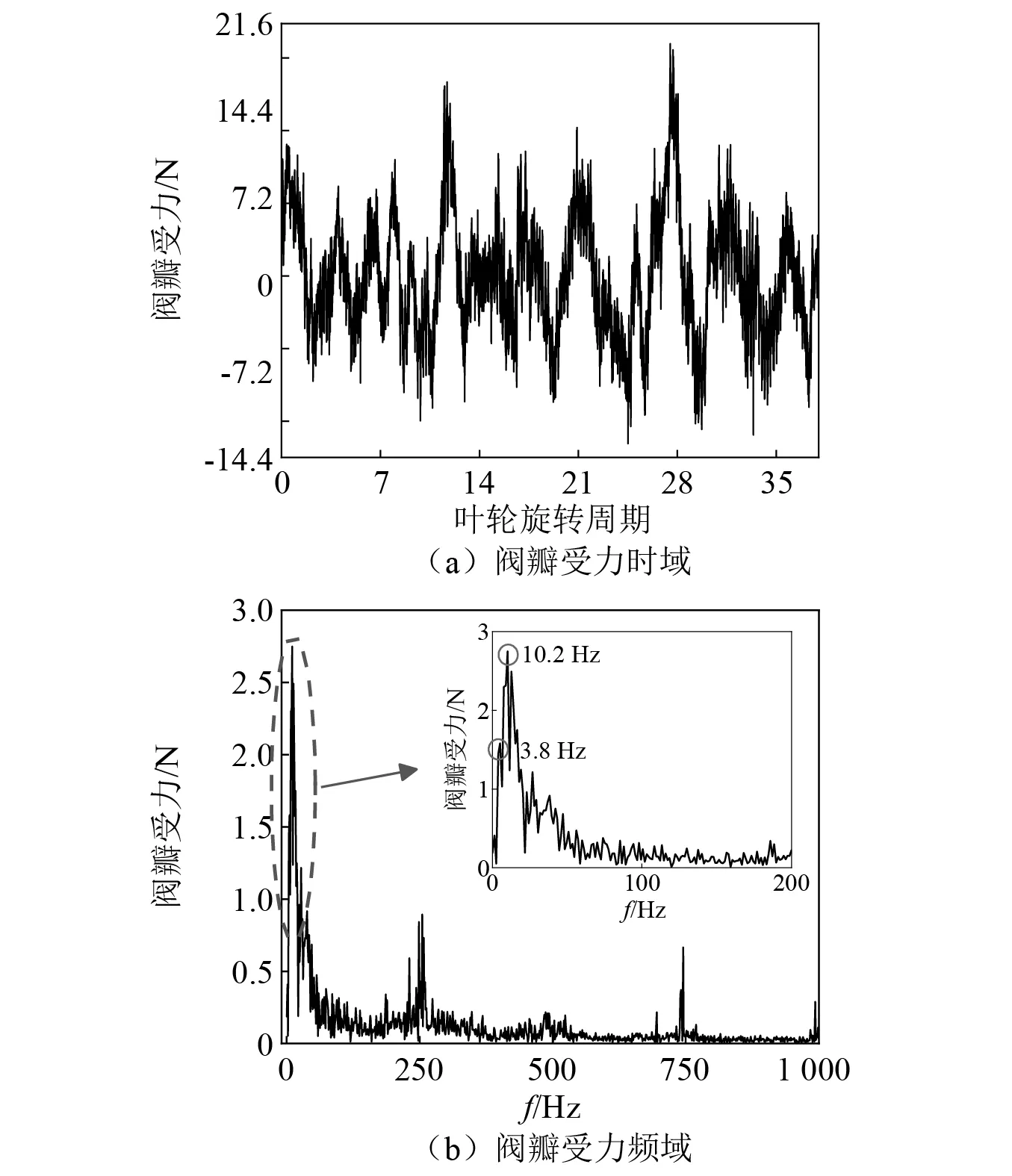
图14 阀瓣受力Fig.14 Force analysis during valve movement
由图15可知,阀瓣运动过程是一个阻尼震荡过程。当阀瓣受到流体介质的压力大于运动部件的重力和弹簧力之和时,此时阀瓣受力为正,阀门加速开启。随着阀瓣上移,其弹簧力作为反作用力逐渐增大。当阀瓣受力为负时,阀瓣速度减小直至反向,阀门渐渐关闭,弹簧力也减小,压差引起的流体力却快速增大。当阀瓣受力为正时,阀瓣下移速度降低并最终正向,实现1个震荡周期。

图15 阀瓣运动规律Fig.15 The law of valve movement
阀瓣运动过程会改变泵阀耦合系统的流量分配,因此需要进一步分析阀瓣位移波动引起的流量脉动。由图16可知,空排口流量与总流量脉动幅值相当,趋势大致相同,但总流量略微滞后于空排口流量,主出口流量脉动不明显。由此可见,在阀瓣运动过程中,阀杆处的节流作用是引起泵阀耦合系统流量脉动的主要原因。

图16 流量分布特性Fig.16 Flow distribution characteristics
3 结 论
本文研究了小流量工况下泵阀耦合系统的非稳态流致激励特性,主要结论如下:
(1) 小流量工况离心泵导叶区域沿着叶轮旋转方向发生周期性堵塞,并以13个叶轮旋转周期为1个导叶失速周期,受其影响,流场内部呈现明显的低频压力脉动。
(2) 阀瓣运动过程是在压差引起的流体力、运动部件重力和弹簧力的平衡过程中实现的,受上游离心泵出口压力波动影响,阀瓣受力始终在正负之间波动,进而引起弹簧止回阀发生颤振现象。
(3) 阀瓣运动过程中,阀杆处的节流作用是引起泵阀耦合系统流量脉动的主要原因。

