基于自适应多可信度多项式混沌-Kriging 模型的高效气动优化方法1)

赵 欢

(西北工业大学航空学院,西安 710072)

引言

随着人们对设计外形的性能表现和可信度要求的不断提高,高可信度计算流体力学(computational fluid dynamics,CFD)数值模拟希望被应用到气动设计中,这使得相同数量样本的CFD 分析计算花费急剧增加,因此急需发展更有效的代理优化方法[1-4].为此,最流行的手段之一就是利用多可信度代理模型代替原来的单可信度代理模型以减少代理建模和优化过程所使用的高可信度样本数量.多可信度代理模型通过使用大量且廉价的低可信度样本建模来反映高可信度模型趋势,并利用少量的高可信度样本对该模型进行修正,从而显著减小构造高可信度代理模型所需的计算花费(更少的高可信度样本数),提高了代理建模和代理优化效率[5].

多可信度代理模型主要有3 种构建方式[6],即加法或乘法标度、混合标度以及空间映射.加法标度相对于乘法标度能够更好地全局近似高可信度分析函数,鲁棒性也更好.典型的如多可信度多项式混沌展开(polynomial chaos expansion,PCE)[7]使用加法标度对低可信度稀疏PCE 中重要项的恢复系数进行修正,以减少所需的高可信度样本数.其建模效率相对于单可信度稀疏PCE 提高一倍多.但多可信度PCE 方法[7]缺乏合适的标准确定多项式矫正项项数,对复杂的问题需要多次试探,从而引入了额外的计算花费.然而,单一的加法或乘法标度缺乏对更多问题的适应性[6],为此研究者又提出了混合标度法,即同时使用加法和乘法标度修正低可信度模型.在各种混合标度法中,两种最流行的形式包括混合桥函数法[8]和类似co-Kriging[9]和分层Kriging(hierarchical Kriging,HK)[10]的贝叶斯估计方法[6].混合桥函数法指使用系数分别对乘法修正因子和加法修正因子进行加权.

相比于混合桥函数法,基于贝叶斯理论的co-Kriging[9]和HK 对许多问题表现出了良好的灵活性和鲁棒性,被广泛用于航空航天系统优化[1]和稳健设计[11]中.co-Kriging 和HK 使用缩放因子和静态高斯随机过程分别作为乘法标度项和加法标度项对低可信度Kriging 模型进行修正,从而获得对高可信度函数的近似.随后,研究者分别将co-Kriging 和HK 推广到任意多层可信度数据建模和优化设计中,优势更加明显.然而对于复杂气动外形精细化设计问题,仍然难以避免相关矩阵规模和条件数过大导致的训练花费过高和精度急剧下降问题.更严重的是,Toal[12]和Zhao 等[13]均发现: 当高、低可信度模型之间偏差较复杂(高非线性/高阶)或高可信度模型是高非线性/高阶时,类似co-Kriging 和HK 等多可信度代理模型使用缩放因子(对低可信度Kriging)和高斯随机过程项难以准确近似这部分复杂(高非线性)偏差.即使使用更多高可信度样本,其建模精度也难以和直接使用高阶多项式作为趋势函数的多项式混沌-Kriging (polynomial chaos-Kriging,PCKriging)等相比,缺乏对飞行器复杂气动设计等许多工程问题所需的建模效率和泛化能力.

不仅如此,低可信度模型的选择对多可信度代理模型的建模效率和精度有显著影响,越好的低可信度模型应该是其与高可信度模型间的偏差越简单或者相对于高可信度模型更低阶[14].然而,越好的低可信度模型可能要求更高的计算花费.Peherstorfer等[6]在多可信度代理模型综述中指出低可信度模型可以通过3 种方式获得,即简化的低可信度模型、基于投影的低可信度模型以及数据拟合的低可信度模型.简化的低可信度模型指通过专业知识对高可信度模型进行适度简化,如在流场特性分析时,可以采用从直接数值模拟(direct numerical simulation,DNS)到大涡模拟(large eddy simulation,LES)、雷诺平均(Reynolds average Navier-Stokes,RANS)、

Euler 方程再到势流方程求解等,或者对于确定的物理方程如RANS,可使用从密网格再到不同密度的稀网格等,他们依次降低可信度和计算花费.而基于投影的低可信度模型指通过数学的方法探测问题内在的结构,比如通过在低维子空间投影得到的降阶模型等.数据拟合类低可信度模型指构建输入到输出的低可信度映射或数学近似模型等,如低阶回归或插值等.不同的多可信度代理模型对低可信度模型的要求和适应性不同,也显著影响了他们的建模效率和泛化能力,越好的多可信度代理模型应该能适应广泛的低可信度模型并提供良好的预测能力.

多可信度代理模型泛化能力的不足也严重影响了代理优化算法的表现[4].为了改进基于多可信度代理模型的优化算法的表现,目前主要包括两方面有潜力工作.其一,改进多可信度代理模型的泛化能力[12].如前所述,当前流行的多可信度代理模型如co-Kriging,HK 以及多可信度多项式混沌(multifidelity polynomial chaos expansion,MF-PCE)等模型在不同问题中表现差异明显.在实际问题中,如果使用不当他们建模和优化效果可能很差.基于此,文献[13,15] 提出了一种自适应多可信度PC-Kriging(multi-fidelity polynomial chaos-Kriging,MF-PCK)代理模型对这一问题进行了有效解决,并通过在复杂数值函数和气动数据建模问题中验证表明: 其相对于流行的通用Kriging,MF-PCE 和HK 等对高非线性/高阶响应的泛化能力更强和建模效率更高.其二,发展更有效的多可信度优化加点准则[16].目前针对多可信度代理优化的加点策略研究仍比较少.Zhang 等[17]针对分层Kriging (HK)模型提出了变可信度期望改进(variable-fidelity expected improvement,VF-EI)加点策略.Huang 等[18]提出通过最大化增广EI (augmented expected improvement,AEI)函数来选取高或低可信度样本点.Jiang 等[19]发展的基于变可信度Kriging 的变可信度置信下届(VF-LCB)准则等.然而,此类多可信度优化加点策略对更多工程实际问题的适应性以及效率并没有得到广泛验证,尤其难以适用于一般多可信度代理模型如多可信度多项式混沌以及多可信度径向基函数等.

如上所述,如何发展新的多可信度代理模型以改进他们的泛化能力,以及改进基于多可信度代理模型的全局优化能力和拓宽应用范围是当前亟需解决的难题.针对第一个难题,本文首先引入了作者提出的自适应多可信度多项式混沌-Kriging (MFPCK) 代理模型[13].该MF-PCK 模型通过结合PCE 的全局近似特性以及Kriging 的局部插值特点,自适应选择最优的多项式基函数和构建最优的多可信度代理模型.该方法已经通过多个复杂数值函数算例和跨音速气动数据建模应用进行了广泛验证,结果均表明,其相对于分层Kriging,PC-Kriging以及多可信度PCE 等流行代理模型全局建模效率和泛化能力均显著提高,尤其对高阶/高非线性等复杂响应的近似准确率提升显著,大大拓展了多可信度代理模型的应用范围和适应性.针对第二个难题,本文发展了基于MF-PCK 代理模型的高维全局气动优化设计新方法,和基于MF-PCK 代理模型的全局优化加点方法,显著改进了多可信度代理优化算法的优化效率和优化能力.为了验证新方法的表现,本文将其应用在经典的数值算例,以及跨音速气动外形确定性优化和复杂的气动稳健优化设计应用中.结果均表明,基于MF-PCK 代理模型的优化方法相对于基于Kriging 的代理优化算法效率提高超过一倍,并且结果更好也更可靠.该方法的成功验证为未来发展基于MF-PCK 代理模型的大规模变量全局优化设计新方法奠定了基础[20],也为解决当前多可信度代理优化算法适应范围窄的难题提供了新思路.

1 自适应多可信度PC-Kriging 代理模型

在气动特性数值分析中,CFD 模拟根据所使用的网格数量,控制方程及近似假设等不同可以提供多个可信度系列样本数据.低可信度模型能提供相对于高可信度模型可参考的趋势,并且越低可信度的模型其计算花费也通常显著更低.利用数量充足但计算花费非常低的低可信度样本来训练趋势模型将大大减少多可信度代理模型的建模花费.本文结合多可信度建模技术发展了一种更加高效的代理建模途径.

1.1 多可信度多项式混沌-Kriging 模型近似

多可信度建模技术通过有技巧地利用充足但廉价的低可信度数据去辅助多可信度代理建模,在提高代理建模精度的同时,显著降低计算花费[6-7,14,21].为此,提出一种全新的混合标度形式来矫正低可信度PC-Kriging 模型[13],即

其中 α0为多乘标度因子,其暗示了高、低可信度模型之间的相关性,C(X) 为增加标度项.代表低可信度PC-Kriging 预测器.MF-PCK 使用基于LAR的低可信度PC-Kriging 作为预测模型,即

式 中rl=[R(X(1),X),R(X(2),X),···,R(X(Nl),X)]T表 示低可信度观测样本Sl与未知点X之间的相关向量,他们的计算均需要代入低可信度模型相关的超参数θl和ql,具体可参考文献[13,22].

在式(1)中,yc(X)是对低可信度PCE 的矫正修正项.多项式校正展开项表达如下

其中 αci和Ac分别表示校正展开多项式项系数和相应的多项式项索引集合.式(3)中校正展开多项式项必须是低可信度PC-Kriging 模型中多项式项的子集.本文设计了一种新的基于嵌套留一交叉验证(leave-one-out cross-validation,LOOCV)的LAR 自适应基函数选择方法(即Nested LOOCV-LAR),详情可见1.2 节.

通过标准“universal Kriging”拟合过程即可得到MF-PCK 在未知点的预测模型,可参考前期工作[13],得到MF-PCK 预测模型在未知点X的预测值为

1.2 基于LOOCV-LAR 的自适应基函数选择方法

为了构建最优的MF-PCK 预测模型,本节设计了一个基于嵌套留一交叉验证−最小角回归(nested LOOCV-based LAR,LOOCV-LAR)方法来选择最优的多项式项集合,以建立最优的MF-PCK 预测模型.该方法详细步骤如下.

2 基于MF-PCK 模型的自适应加点优化方法

2.1 基于MF-PCK 代理模型的优化流程

如上所述,相对于单可信度代理模型,为了相同的近似准确率,多可信度代理模型能显著减少计算花费.因此,应用多可信度代理模型到气动优化中能使高、低精度的样本数据有机结合,以平衡分别基于高、低可信度数据优化的差异,减少迭代周期和总花费.本文以第1 节提出的自适应MFPCK 代理模型为基础,发展基于变可信度模型的加点准则.基于MF-PCK 代理模型的优化流程图如图2 所示.

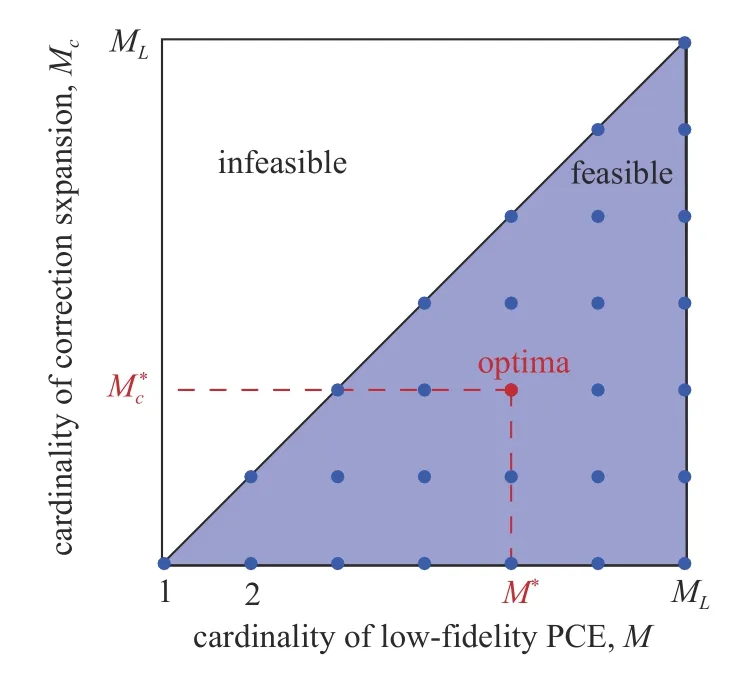
图1 自适应选择最相关的低可信度多项式集合和最优的矫正多项式集合图示说明Fig.1 Sketch map in selecting the optimal cardinalities of the lowfidelity PCE and corresponding correction expansion for the optimal MFPCK model

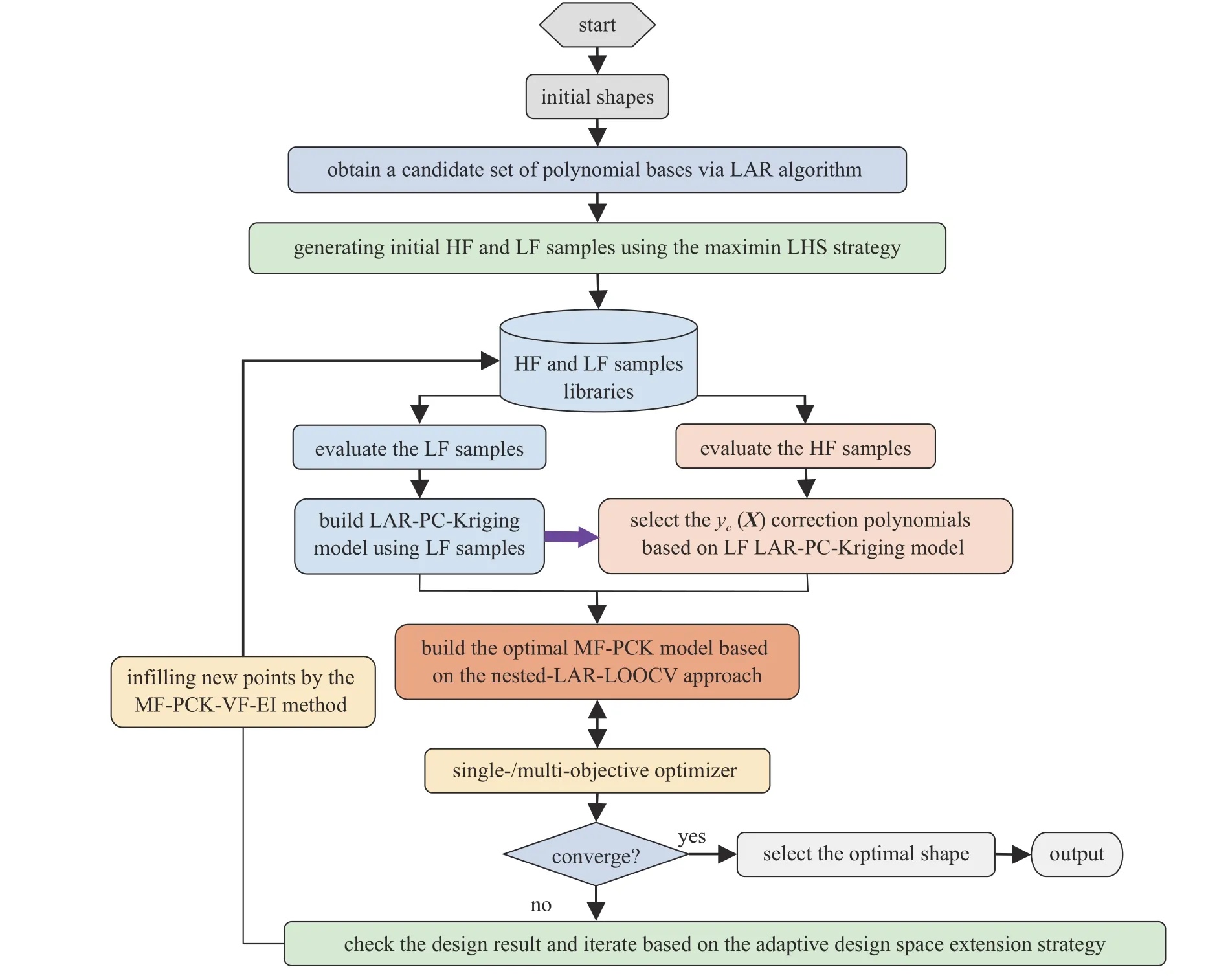
图2 基于自适应MF-PCK 的多可信度气动优化流程图Fig.2 The flow chart of adaptive MF-PCK-based multi-fidelity aerodynamic optimization algorithm

2.2 变可信度期望改进加点方法

变可信度期望改进(VF-EI)加点策略是基于基本的EI 加点方法和分层Kriging 方法发展而来的[17],本文在此基础上发展了基于新型MF-PCK 的VFEI 加点策略.由第1 节发展的MF-PCK 预测器在任意点X的预测值为

则在任意点的均方差预测(MSE)为

在VF-EI 中,MF-PCK 预测的不确定性被定义为

相对于基于HK 定义的VF-EI 加点方法[17],基于MF-PCK 的VF-EI 方法能提供更好的全局趋势预测能力和局部空间预测精度.这是因为分层Kriging和co-Kriging 等模型仅仅使用缩放因子和高斯随机过程去建模高、低可信度模型之间的差异部分,而广泛的工程问题中高、低可信度模型之间的差异是非常复杂和高非线性的,这使得他们难以提供准确的趋势预测模型,也就导致了他们的均方差预测无法准确暗示误差最大位置.而MF-PCK 模型使用低可信度PC-Kriging 和高可信度矫正展开多项式可以准确地近似高可信度函数趋势部分,高斯随机过程可以精确模拟剩余残差,使得MF-PCK 均方差预测和预测误差一致性更好,近似高可信度模型的准确率也显著更高[13],更多详细的分析和验证可参考课题组相关的文献[13].通过相似的方式[24],可以得到目标函数改进的期望为

然后在VF-EI 加点过程中的子优化就为寻找合适的加点位置以及可信度水平使VF-EI 最大,即

其中 gj表示约束函数,mc为约束函数个数.

3 优化应用验证

为了检测提出的MF-PCK 代理模型在优化设计中的表现,本节分别使用一个典型函数优化算例和两个气动优化应用进行测试.基于MF-PCK 代理模型的优化过程使用VF-EI 加点策略(MF-PCK_VFEI),并与使用基于Kriging 的EI (Kriging_EI)加点算法和使用基于分层Kriging (HK)的VF-EI (HK_VFEI)加点算法进行对比,3 种优化方法均使用全局加强学习粒子群(comprehensive learning particle swarm optimizer,CLPSO)算法.

3.1 函数优化测试

测试函数使用Branin 函数,其表达式为

相应的低可信度表达为

Branin 函数的函数值分布如图3 所示,图中红色实心点表示3 个最小值位置,最小值均为0.397887,最小值位置分别为 (−π,12.275),(π,2.275)以 及 (9.42 478,2.475).对应Branin 函数的低可信度函数如图4 所示.对基于MF-PCK_VF-EI 和HK_VF-EI 的多可信度优化过程,通过拉丁超立方抽样(Latin hypercube sampling,LHS) 分别选取5 个高可信度样本点和50 个低可信度样本点作为初始样本点,而基于Kriging_EI 的代理优化过程选取10 个高可信度样本点作为初始样本.3 种方法均使用全局加强学习粒子群(CLPSO) 优化算法.当两种方法分别添加50 个高可信度样本点时,结果均接近收敛,高可信度样本点对比分布如图5～ 图7 所示.基于MF-PCK_VF-EI 和HK_VF-EI 的方法在3 个极值点附近均添加了更多样本点,而基于Kriging_EI 的方法添加样本点的位置仍然变化较大.图8 给出了函数值收敛过程对比,明显可以看出,基于MF-PCK_VF-EI 的方法优化过程收敛最快,其次是基于HK_VF-EI 的方法,并且两种多可信度代理优化方法均较基于Kriging_EI 的优化算法收敛更快.基于MF-PCK_VF-EI的优化方法在添加了20 个高可信度样本以后就已经收敛,而基于HK_VF-EI 和Kriging_EI 的优化方法则分别需要添加37 和40 个高可信度样本以后才接近收敛.图9 给出了每次加点位置处预测误差对比曲线.可以看出,基于MF-PCK_VF-EI 方法的预测误差明显小于基于HK_VF-EI 和Kriging_EI 方法的预测误差,并且较早收敛;而基于HK_VF-EI 和Kriging_EI 的方法都需要添加到40 个样本以后,预测误差才不再明显波动.表1 给出了3 种方法找到的最优位置和最优值对比,可以看出,在相同较少的计算花费下,基于MF-PCK 的方法找到的最优值低于基于HK_VF-EI 和Kriging_EI 的方法找到的最优值,他们找到的位置也有较大区别.

图3 Branin 函数及最优值位置Fig.3 The Branin function contour

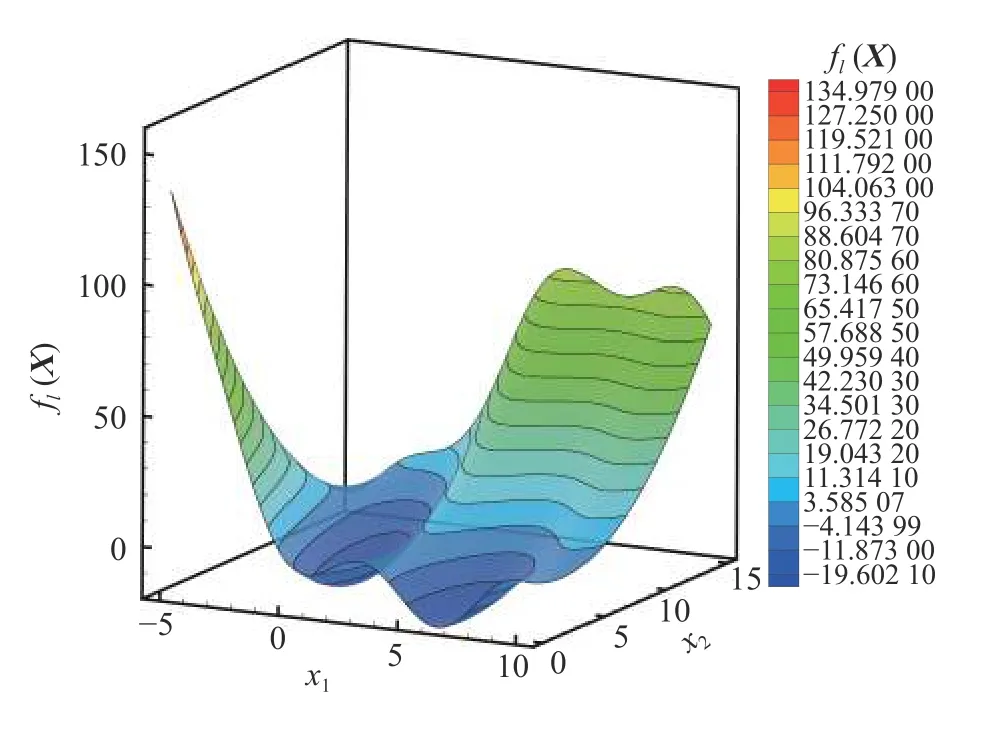
图4 近似Branin 函数的低可信度函数Fig.4 The corresponding LF function of Branin function

图5 基于Kriging_EI 加点过程Fig.5 The infilling process of Kriging_EI optimization method

图6 基于HK_VF-EI 的加点过程Fig.6 The infilling process of HK_VF-EI optimization method

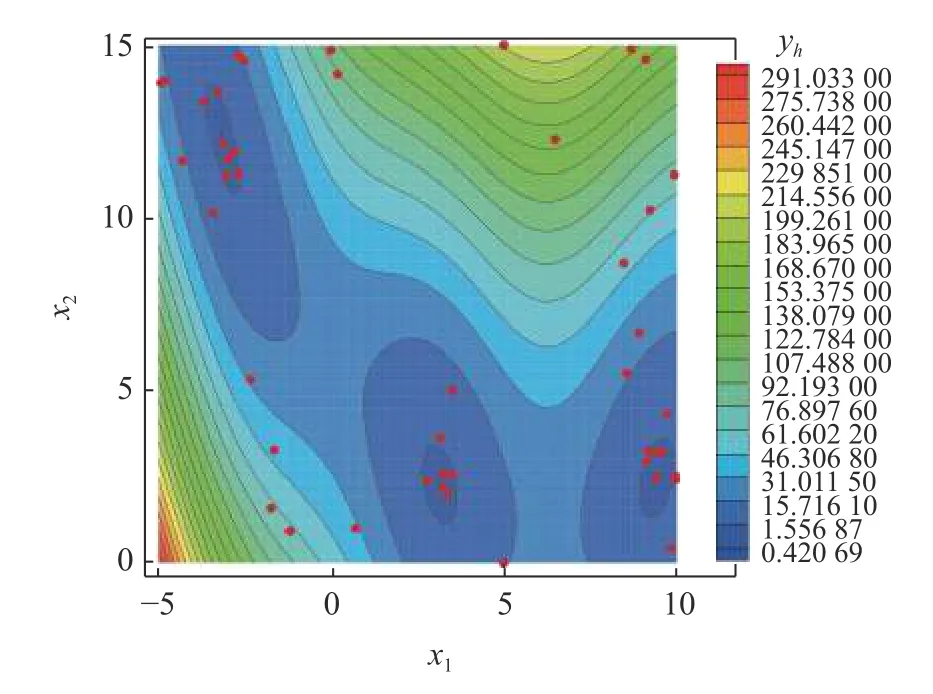
图7 基于MF-PCK_VF-EI 的加点过程Fig.7 The infilling process of MF-PCK_VF-EI optimization method

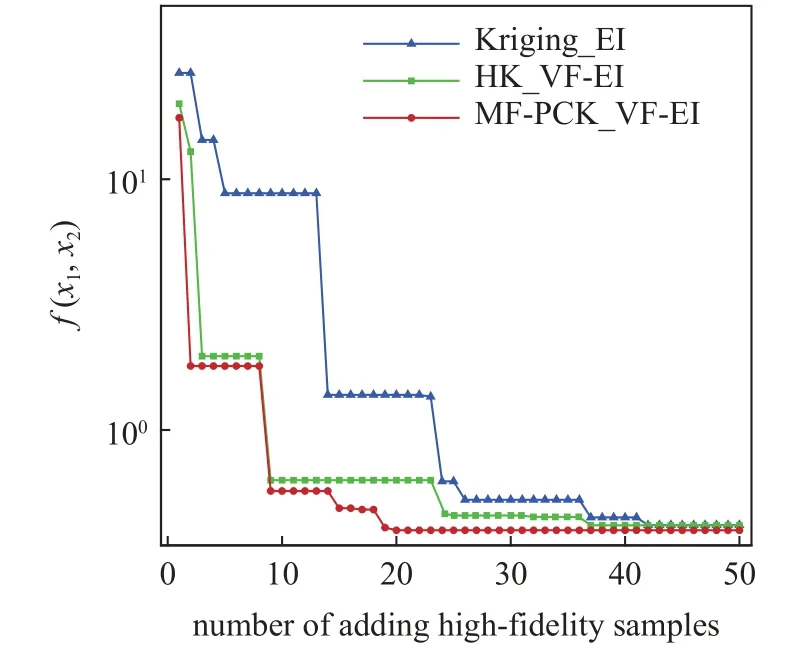
图8 函数值收敛过程对比Fig.8 The convergence history of the function values

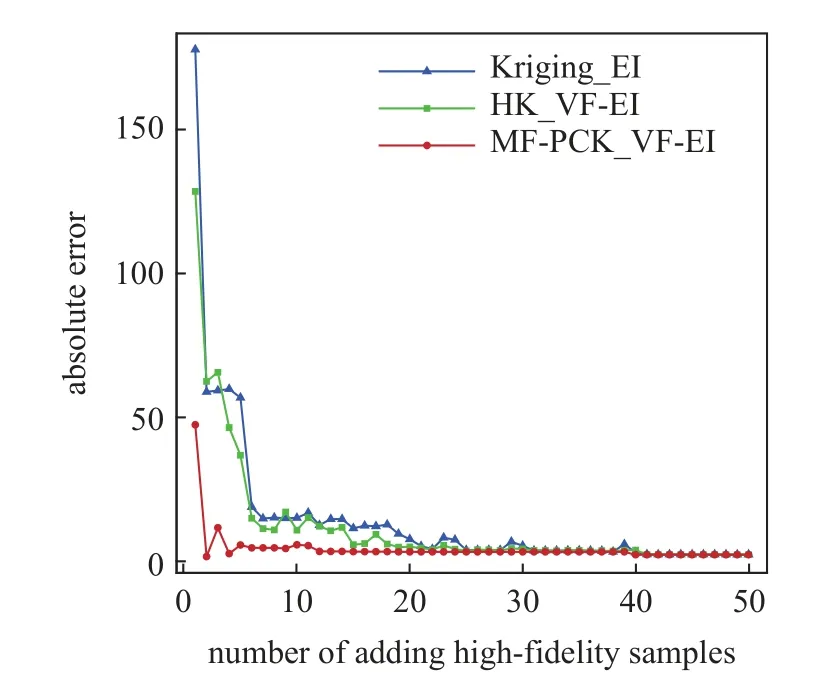
图9 代理模型预测误差收敛过程对比Fig.9 The convergence history of the surrogate prediction errors

表1 3 种优化方法结果对比Table 1 Comparison of optimization results using three methods

3.2 跨音速气动优化应用

3.2.1 跨音速RAE2822 翼型优化设计

首先测试了针对RAE2822 翼型的不同网格水平的计算结果.网格为C 型拓扑,远场距离为50 倍翼型弦长,湍流模型均使用两方程SST.不同网格量网格近场分布如图10 所示.远场网格分布如图11所示.选取的典型计算状态为:Ma=0.734,Re=6.5×106,以及Cl=0.824(α=2.79◦).图12 给出了数值模拟结果与试验值压力分布对比.可以看出,随着网格密度增加,数值模拟结果与试验结果吻合越来越好,对激波位置和强度的捕捉也更为准确.表2 给出了数值计算结果与试验气动力系数的对比.结果显示,从稀网格(L1水平)增加到中等网格(L3水平),网格量增加了接近20.25 倍,阻力系数误差降低了17.22%.继续增加网格量到密网格(L5水平),网格量增加了49.5 倍,阻力系数降低了18.80%,而与L3水平仅仅相差了1.58%,压力系数分布接近收敛.因此本文分别使用L1水平和L3水平为低可信度和高可信度样本CFD 分析网格,使用L5水平网格作为优化外形气动特性检验网格,以满足高效气动优化设计需求.

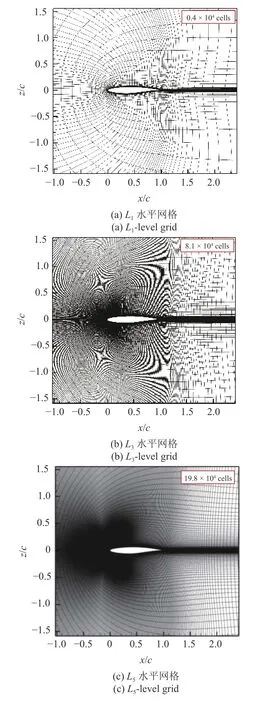
图10 针对RAE2822 翼型的不同可信度水平计算网格Fig.10 Different levels of fidelity grids around RAE2822 airfoil

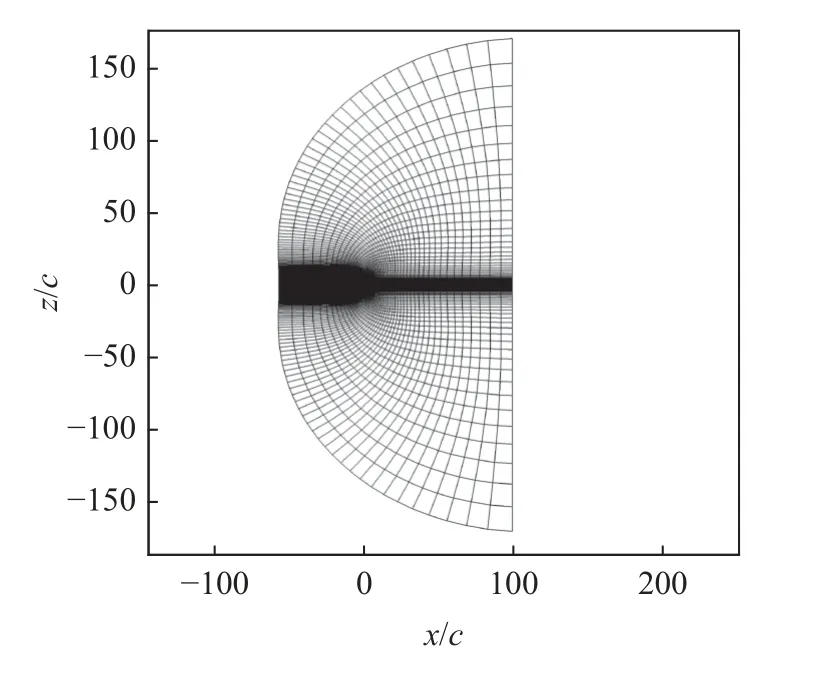
图11 高可信度网格远场图Fig.11 Far view of the high-fidelity grid

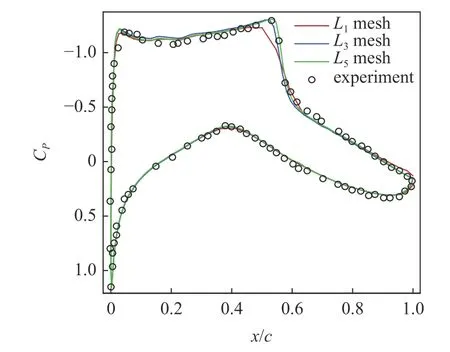
图12 不同网格量计算压力分布与试验压力分布对比Fig.12 Comparison of pressure distributions among computational and experimental results

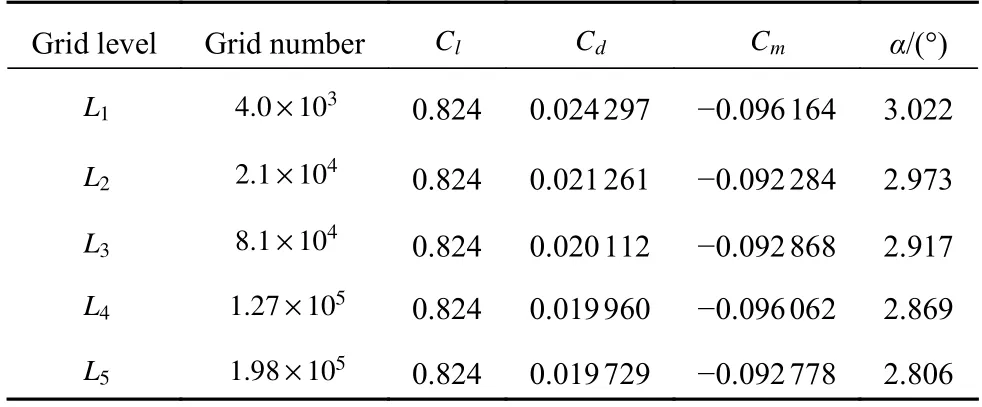
表2 RAE2822 网格收敛结果对比Table 2 Comparison of computational results of different levels of grids

为了对比说明,本节基于单可信度Kriging 模型的初始样本为Nh=40,即计算花费为4 0t.而基于MF-PCK 模型的方法使用课题组提出的基于留一交叉验证-Voronoi-最大尺度距离(LOOCV-Voronoi-MSD)的序列抽样方法[13]从Nh=1和Nl=10开始自适应选样直到获得相同计算花费(4 0t)的高、低可信度样本分布和样本数量,即使用Nh=15个高可信度样本和Nl=500 个低可信度样本.其中t表示一次高可信度CFD 计算分析时间,高、低可信度数值分析均使用RANS 数值求解器求解.设计状态为Ma=0.734,Cl=0.824,Re=6.5×106.设计约束包括升力系数、力矩系数和面积均不减小,优化模型为

本算例使用SST 湍流模型进行气动分析,初始翼型阻力为0.02171.采用类函数/形函数(class/shape transformation,CST)参数化方法控制翼型变形,上下表面各选取12 个设计变量,共24 个变量,初始设计范围如图13 所示.3 种方法均使用全局加强学习粒子群(CLPSO)优化算法.基于MF-PCK_VF-EI 的优化流程如图2 所示,迭代加点70 次.图14 给出了3 种方法阻力系数收敛曲线对比,可以看出,相比于基于Kriging_EI 和HK_VF-EI 的两种优化方法,基于MF-PCK_VF-EI 的代理优化算法获得了最快的收敛速度以及最低的阻力适应值,在迭代到第30 次高可信度加点时,阻力系数已经收敛;而基于HK_VF-EI 的优化算法则需要迭代加点到50 个高可信度加点时才逐渐收敛;基于Kriging_EI的代理优化方法收敛速度最慢,直到第70 次迭代加点时阻力系数仍在少量下降.从图15 可以找出原因,MF-PCK 代理模型在迭代过程中持续拥有更准确的预测精度,从第30 次高可信度加点以后,加点位置处阻力系数预测误差在0.0002 以内,而HK 和Kriging 代理模型阻力系数预测误差仍然在0.0006较大范围以内波动.MF-PCK 模型使用了较多的低可信度样本,可以更准确地捕捉整个设计空间的特点.在Kriging_EI 加点过程中,由于EI 搜索兼具了提高全局近似准确率的特性,造成了加点位置波动较大.当加点样本较少时,Kriging 代理模型本身的近似不足,进而造成最优位置以及近似误差的波动.随着基于Kriging_EI 的加点过程进行,优化目标值和代理预测误差均逐渐收敛,但优化目标的收敛却慢于代理预测误差的收敛,这与EI 加点过程后期收敛性变差密切相关,当代理预测误差和优化目标均收敛时,该优化过程趋于收敛,得到收敛外形.表3给出了基于3 种代理模型的优化算法在接近收敛时的总计算时间和气动力系数对比.基于MF-PCK_VF-EI 的代理优化方法在第30 次高可信度加点时阻力系数已经收敛,收敛阻力系数值为111.82 counts,总计算时间(初始样本和新添加样本的CFD 分析时间)约等于 7 0t;而基于HK_VF-EI 和Kriging_EI 的代理的优化方法分别在第50 次和第70 次加点时阻力系数在接近收敛,收敛的阻力系数值分别为112.82 counts 和113.75 counts,总计算时间分别约等于 9 0t和1 10t.因此,基于MF-PCK 的代理优化方法相对于HK_VF-EI 和Kriging_EI 等两种经典代理优化方法在更短时间内获得了阻力值更低的翼型,效率和可靠性均显著提升.此外,因为在基于MFPCK_VF-EI 的优化过程中,子迭代自适应选择和分析低可信度样本点的计算花费非常低,其相对于添加高可信度样本点的花费可忽略不计,因此本文忽略了加点过程中低可信度样本的计算花费.图16 给出了优化翼型和RAE2822 翼型外形对比,可以看出基于MF-PCK_VF-EI 的方法优化的翼型较基于Kriging_EI 方法优化的翼型最大厚度位置略有后移,弯度略有增加.图17 给出了4 个翼型的压力分布对比,可以看出,基于MF-PCK_VF-EI 的方法优化的翼型激波几乎完全抹平.

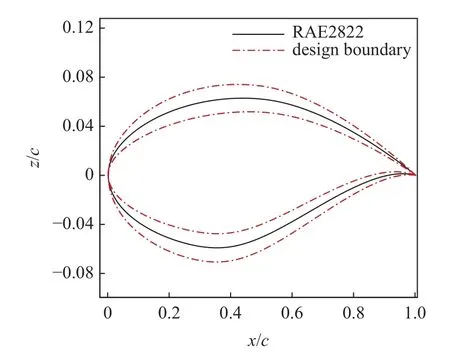
图13 翼型设计空间展示Fig.13 The design space of airfoil

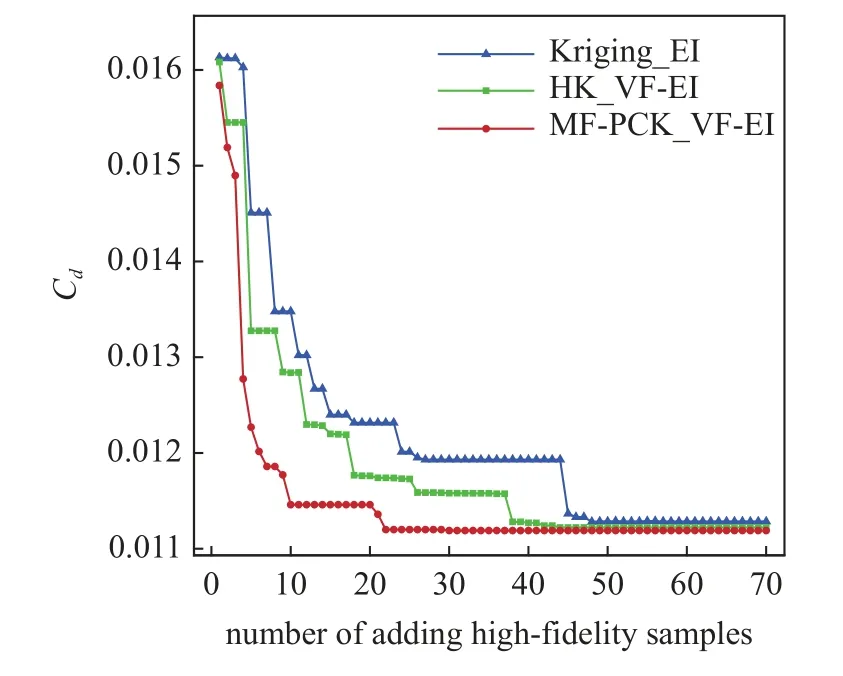
图14 阻力系数收敛过程Fig.14 The convergence history of drag coefficients

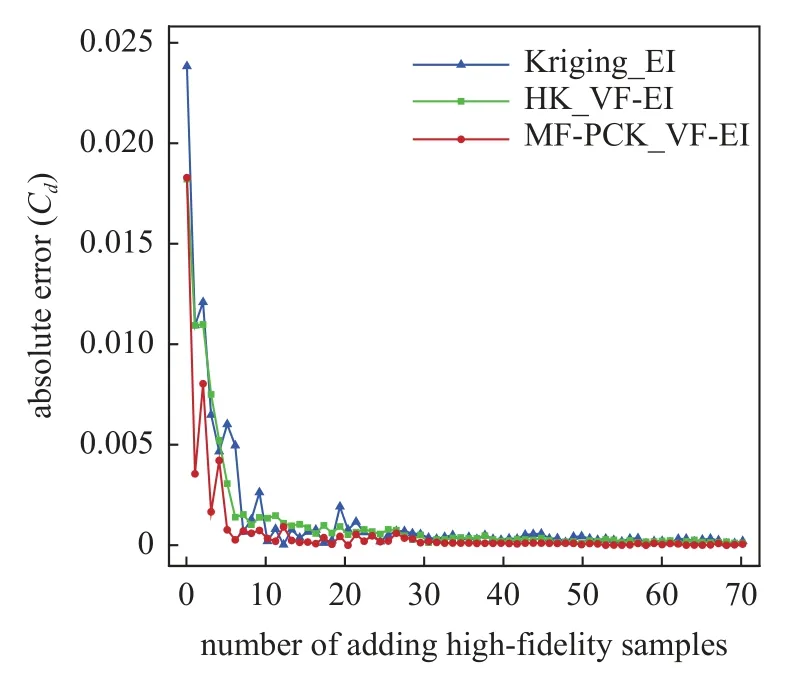
图15 阻力系数代理模型预测误差收敛过程Fig.15 The convergence history of surrogate prediction errors of drag coefficients

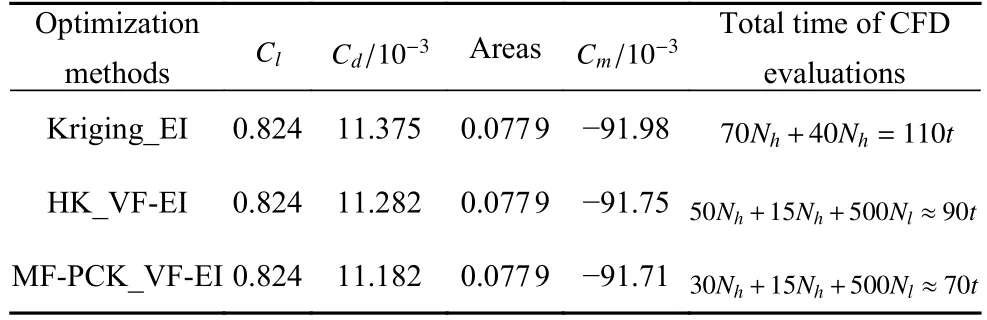
表3 RAE2822 翼型优化设计结果对比Table 3 Comparison of optimization results of RAE2822 airfoil

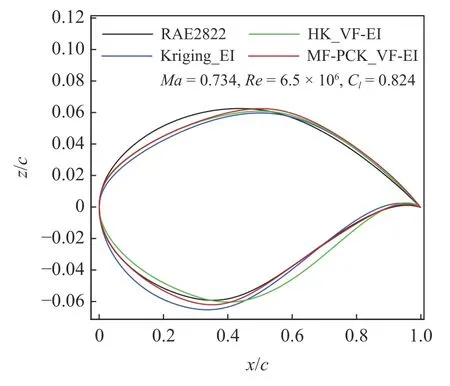
图16 优化翼型与初始翼型外形对比Fig.16 Comparison of optimized and initial airfoils

图17 优化翼型压力分布对比Fig.17 Comparison of pressure distributions of optimized and initial airfoils

3.2.2 跨音速RAE2822 翼型稳健优化设计

然而当考察单点优化得到的翼型在非设计点表现时,结果如图18 所示.单点优化翼型在非设计点阻力剧烈增加,其气动表现对马赫数、升力系数等状态参数波动非常敏感,因而难以被工程使用.针对这个问题,稳健优化是最有希望的解决途径[25-27].然而,稳健优化是一个典型的双循环过程[26,28],外循环为优化设计循环,内循环在迭代的每一步对每个候选设计(粒子)进行不确定分析,得出量化的不确定量,如均值和方差等.这使得即使在内循环使用高效的不确定分析方法,如PCE,但依然不可避免的要求远远更多的计算花费,远超过基于代理的确定性优化[11,29].针对这个问题,本文构建关于设计变量与随机变量的联合代理模型,使得在搜索过程中通过调用此代理模型对每个候选设计进行不确定分析,从而大大减少了计算花费[30-31].定义上述问题的稳健优化模型为

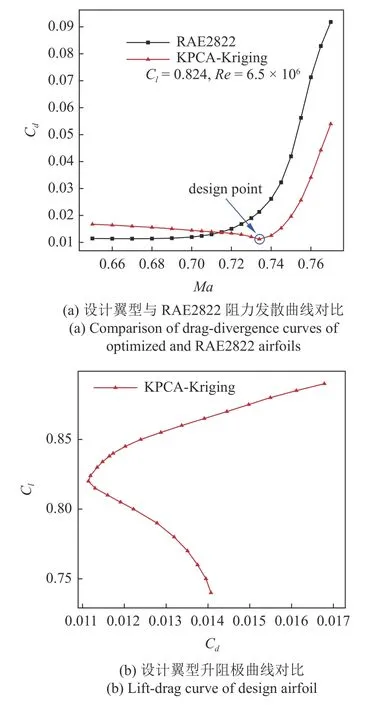
图18 单点优化设计翼型在非设计点气动特性对比Fig.18 Comparison of aerodynamic characteristics of optimized airfoil on off-design points

对该优化问题首先构建马赫数Ma∈[0.7,0.75]与设计变量xi∈[−0.03,0.03](i=1,2,···,24)共25 个变量的联合代理模型S(Ma,x1,x2,···,x24),其中设计变量设计范围如图13 所示.在联合代理模型构建后,在迭代的每一步,每个候选设计的表现不确定量化可通过下式估算

其中 Ξ 代表了不确定因素,如Ma.

通过LHS 抽样选取100 个混合变量高可信度样本以及1000 个混合变量低可信度样本,构建联合代理模型.此时,MF-PCK 预测力矩系数均值和标准差RRMSE 分别为0.00364 和0.01935,完全可以满足优化设计使用.然后使用全局加强学习粒子群(CLPSO)优化算法优化迭代1000 次,得到如图19 所示稳健优化翼型.可以发现,相比于单点优化翼型,最大厚度位置后移,前缘半径变小.图20 给出了稳健设计翼型与单点优化翼型及初始翼型阻力发散特性对比.可以看出,稳健优化翼型阻力发散马赫数超过0.75,高于其他两个翼型,并且在马赫数0.70～ 0.75范围内阻力系数变化更加稳健.图21 给出了稳健设计翼型与其他两个翼型在不同马赫数下压力分布对比.在0.734 马赫数下,稳健优化翼型上表面出现一个双弱激波,在0.75 马赫数下,稳健优化翼型也出现了一个双弱激波,强度均明显弱于单点设计翼型的强激波.因此,通过稳健设计优化,RAE2822 翼型上表面出现了稳定的双弱激波,从而提高了对马赫数的稳健性.然而,针对其他气动外形设计算例,双弱激波是否具有对马赫数等的稳健性,仍然值得更多详细研究.

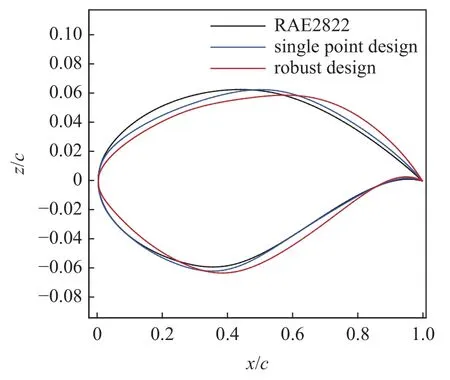
图19 优化翼型与初始翼型外形对比Fig.19 Comparison of optimized and initial airfoils

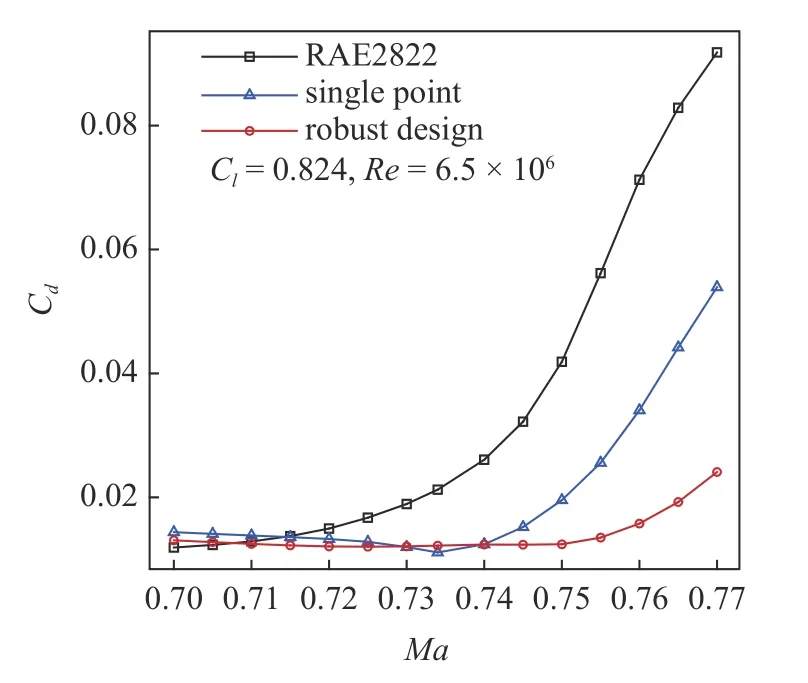
图20 优化翼型阻力发散特性对比Fig.20 Comparison of drag-divergence characteristics of optimized and initial airfoils

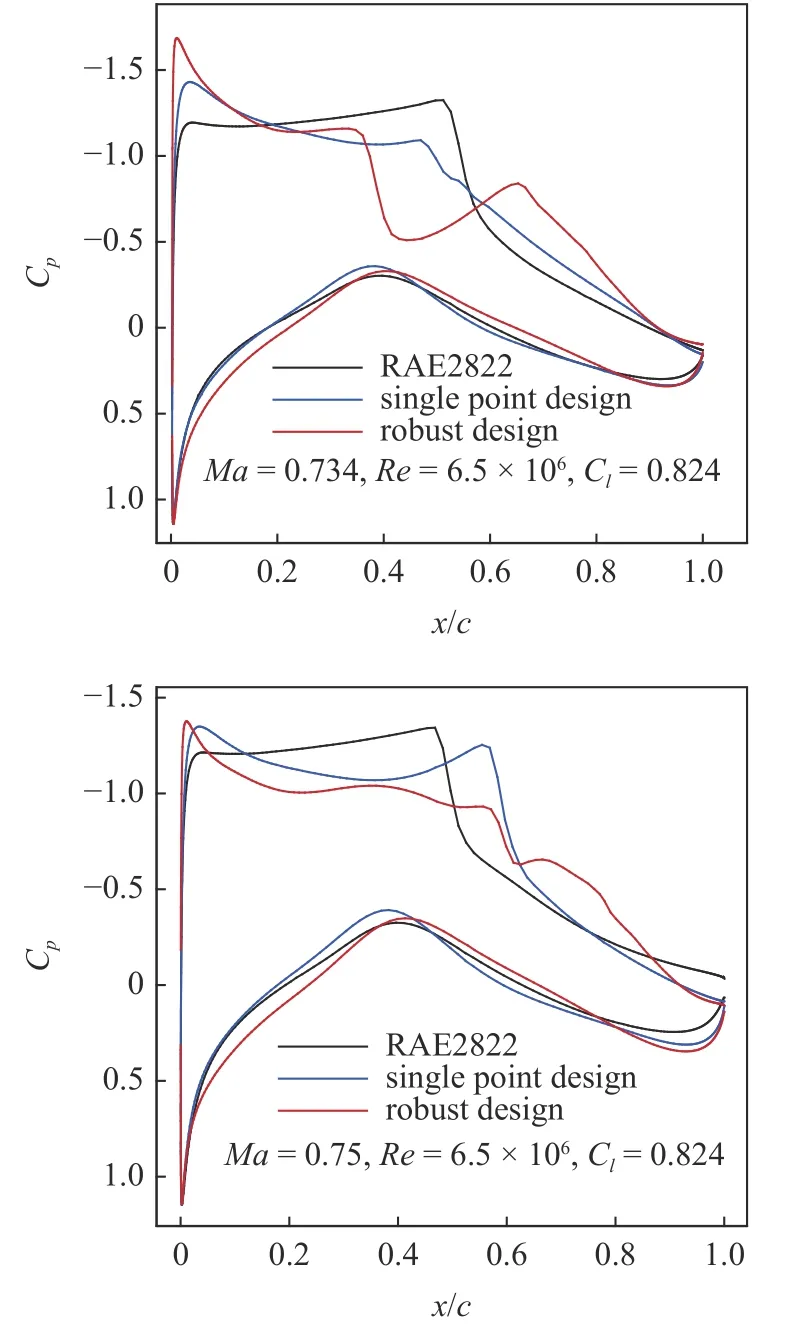
图21 优化翼型与RAE2822 翼型在不同状态下压力分布对比Fig.21 Comparison of pressure distributions of optimized and initial airfoils under different Mach numbers

3.2.3 跨音速ONERA M6 机翼优化设计

跨音速ONERA M6 机翼经常被用来测试数值计算程序或者优化算法的可靠性.本算例考虑的计算状态为Ma=0.839 5,Re=1.172×107,α=3.06◦.该状态下,ONERA M6 机翼上表面有较强激波.首先使用3 套不同网格量计算网格验证计算程序的可靠性,计算网格分布如图22 所示.图23 分别给出了41%和63%位置处剖面压力分布对比,可以看出,640 W 网格和试验压力分布吻合良好,而320 W 网格计算结果接近640 W 网格计算结果,30 W 网格计算结果能捕捉到激波基本位置.正如第1 节指出,低可信度计算网格的选择应该以能较为准确地捕捉到高可信度计算的趋势为准.因此,在本算例中,高可信度气动分析使用网格量为320 W 的计算网格,而低可信度计算使用网格量为30 W 的网格,两者在相同计算资源下,计算时间相差10.67 倍.本算例均使用SST 湍流模型进行计算,高可信度计算初始机翼阻力为113.97 counts,升力系数为0.1670.设计问题定义为在机翼各个剖面最大厚度和机翼升力系数不减小的情况下最小化机翼阻力系数,其优化数学模型为

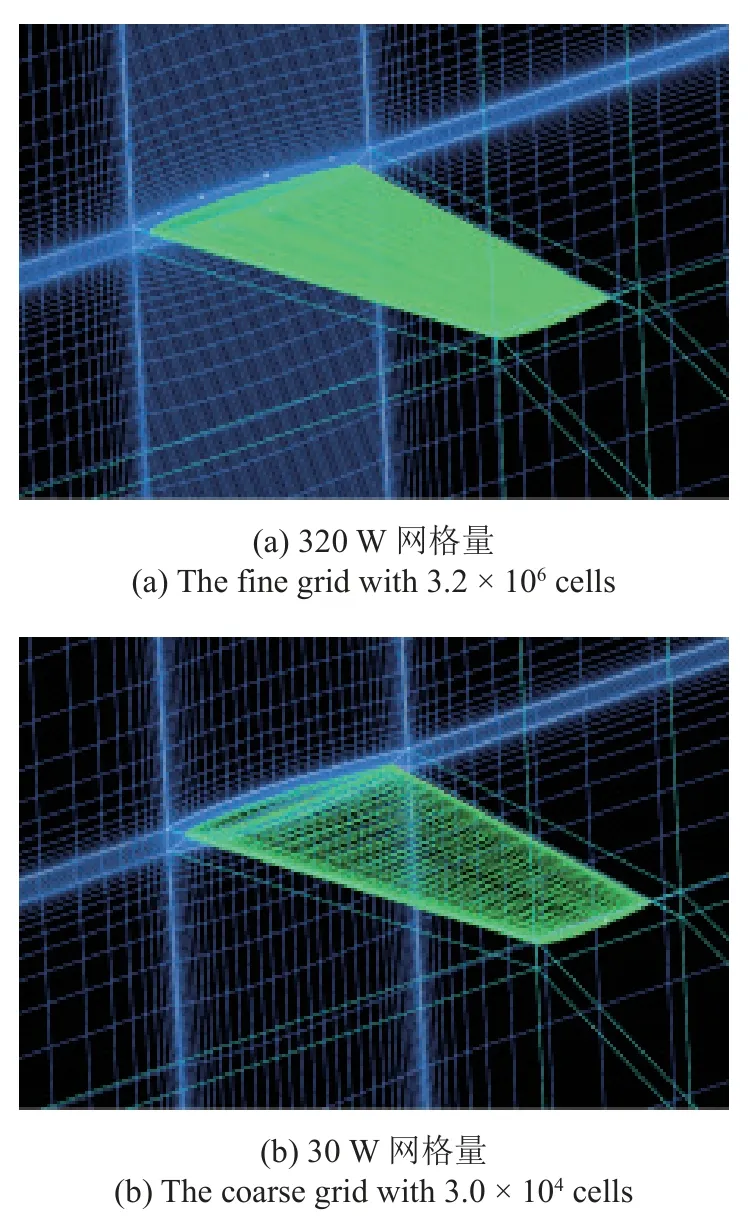
图22 M6 机翼CFD 计算空间网格展示Fig.22 Computational grids of M6 wing

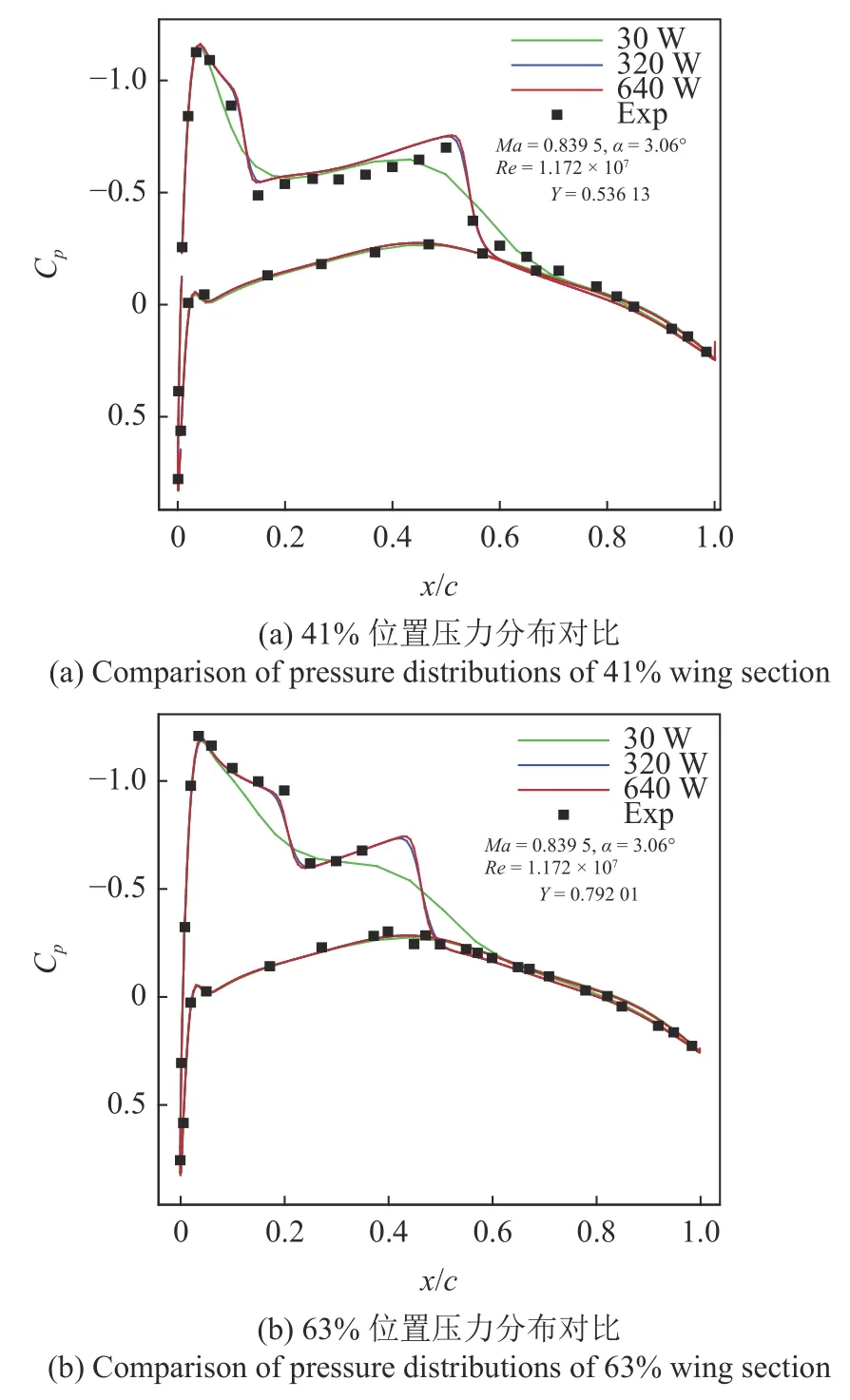
图23 不同计算网格量下计算压力分布与试验压力分布对比Fig.23 Comparison of computational and experimental pressure distributions under different number of grids

采用自由变形(free form deformation,FFD)方法对机翼进行参数化,如图24 所示,选择4 个剖面对机翼进行变形,每个剖面定义了12 个控制点,通过控制每个控制点沿z方向移动从而产生新外形,机翼剖面不扭转.针对基于MF-PCK_VF-EI 的代理优化方法,采用LHS 产生Nini,h=d×2=96个初始高可信度样本,以及Nini,l=d×20=960个初始低可信度样本,采用VF-EI 加点方法进行优化.两种方法均使用全局加强学习粒子群(CLPSO)优化算法.作为对比,针对基于Kriging 代理模型的优化方法使用LHS 产生Nini=d×5=240个初始高可信度样本,采用EI 加点优化方法,其中d为设计变量数.图25 给出了两种方法阻力收敛历程对比.结果显示,基于MF-PCK 的代理优化方法随着高可信度样本填充,具有更快的收敛速度,到78 次高可信度加点时阻力已经收敛到98.07 counts,阻力下降了15.9 counts;而基于Kriging_EI 的代理优化方法收敛很慢,直到200 次加点时阻力才收敛到99.04 counts.因此,基于提出的多可信度代理模型采用更少的计算花费获得了更好的收敛解,大大提高了代理优化收敛速度以及获得更优解的效率(优化效率提高了一倍多).图26 给出了初始M6 机翼和(基于MF-PCK)代理优化的机翼上表面压力云图对比.可以看出,优化的机翼基本消除了原始机翼上表面的两道强激波,仅仅在局部位置存在非常弱的激波.可以发现到接近收敛时,每一次迭代阻力值下降很小.这是因为在无激波外形附近,阻力值变化接近平坦,随机搜索算法效率很低.图27 给出了4 个剖面位置处的压力分布和剖面翼型对比,强激波已经消除.设计结果再次验证了提出的方法相对于基于Kriging_EI 的代理优化方法的有效性和巨大优势.

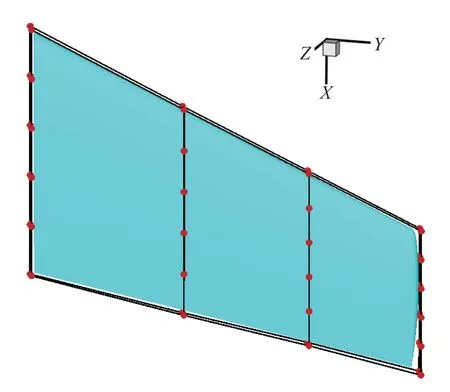
图24 M6 机翼FFD 框Fig.24 FFD frame of M6 wing

图25 两种方法阻力收敛历程对比Fig.25 The convergence history of different optimization algorithms

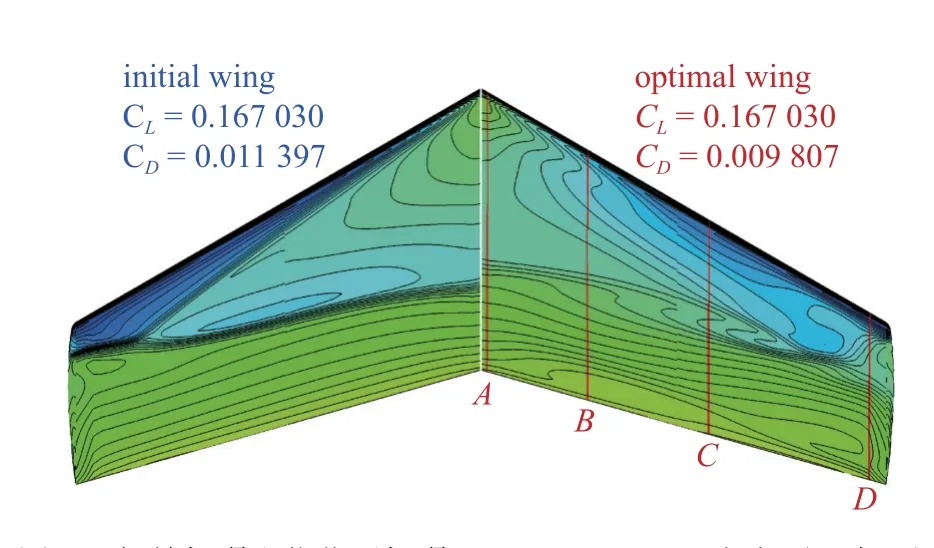
图26 初始机翼和优化后机翼(MF-PCK_VF-EI)上表面压力云图对比Fig.26 Comparison of pressure distribution contours of upper surface of M6 wing using the MF-PCK_VF-EI method

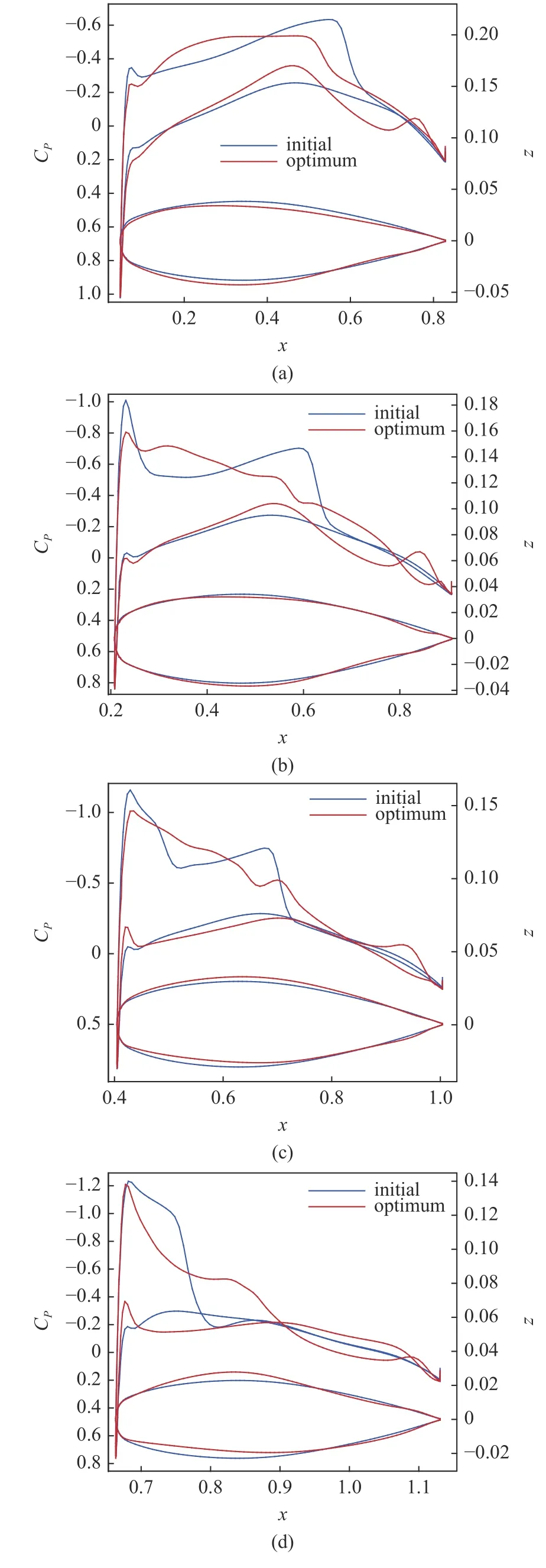
图27 初始机翼和优化后的机翼(MF-PCK_VF-EI)各剖面压力分布和翼型对比Fig.27 Comparison of pressure distributions and shapes of initial and optimized wing sections

4 总结

本文针对基于代理模型的全局气动优化方法效率低下和CFD 可信度要求不断提高带来的优化设计难题,提出了基于新型自适应多可信度多项式混沌-Kriging (MF-PCK)代理模型的高效全局气动优化方法和框架.本文详细推导了建模过程及构建步骤,并陈述了优化框架中的关键模块和技术难点.通过使用相同标度形式再次矫正MF-PCK 模型,该方法也可用于3 层及以上多水平多可信度气动数据建模和优化设计中.同时本文提出了基于MF-PCK 模型的变可信度期望改进加点优化方法,其在每次加点迭代过程中能自适应地选择高可信度或低可信度样本添加到样本库中,提高优化过程中气动分析效率,从而进一步提升多可信度全局气动优化效率和能力.最后本文将发展的框架应用到RAE2822 翼型和M6 机翼的单点确定性设计和RAE2822 翼型的稳健优化设计中,并与基于HK_VF-EI 和Kriging_EI 的代理优化方法进行了全面比较.基于本文气动优化算例的结果显示,基于新型MF-PCK 代理模型的优化方法其优化效率相对于基于HK_VF-EI 和Kriging_EI 的优化效率显著提高,结果更好也更加可靠,并且稳健优化设计效率和结果也更加符合实际工程应用对气动优化方法的要求,从而广泛验证了发展的新方法相对于当前基于HK_VF-EI 和Kriging_EI 的代理优化算法的显著优势和巨大潜力.此外,虽然MF-PCK 模型相比HK 模型等具有更强的泛化能力,但训练时间也更长,未来可通过发展基于多核并行的自适应LOOCV-LAR 基函数选择方法来有效解决.同时当前流行的多可信度代理模型如Co-Kriging,HK 以及MF-PCK 等均遭遇维数灾难难题,未来需要发展更有效的高维空间代理建模技术,如降维代理建模方法等.最后基于MF-PCK 代理模型的优化算法亦缺乏对广泛工程问题的验证,未来需要结合具体的复杂应用来探究它的实际的表现和可能的改进.