弹性/黏弹性混合管道瞬变流参数校核方法
孙强, 王祉皓, 伍悦滨, 徐莹
(1.东北林业大学土木工程学院人工环境与能源应用研究所, 哈尔滨 150040; 2.哈尔滨工业大学建筑学院, 哈尔滨 150090; 3.哈尔滨工业大学寒地建筑科学与工程研究中心, 哈尔滨 150090; 4.哈尔滨商业大学能源与建筑工程学院, 哈尔滨 150028)
有压管道经常会因突然停泵或关阀引起的压力突增或骤降的水力现象,可能导致设备损坏或管道炸裂,这种管内流体的瞬变流动现象,在工程中称之为水锤现象[1-2]。为保证输水系统安全运行,对管道瞬变流动进行分析和控制是学者们重点研究的方向[3-4]。
近些年,随着高分子材料技术的迅猛发展,高分子聚合物管道因其价格低、抗腐蚀性高、节能环保等特点,广泛应用于供水管道系统中。现如今,塑料管道常用于替换传统金属管道,使得现阶段管道系统中经常出现金属管道与塑料管道混合连接的情况。由于塑料管道的力学特性不同于传统金属管道的弹性力学特性,其同时表现出弹性和黏性两种力学行为,因而也被称为黏弹性管道。黏弹性管道在瞬变应力的激励下,所产生的应变可以表示为弹性应变和延迟应变的叠加。这种黏弹力学行为还会影响瞬变流动中压力波动的峰值、相位和衰减。因黏弹性管道力学行为的复杂性,传统弹性管道瞬变流的数学模型已不再适用于黏弹性管道瞬变流的数值模拟。近些年来,学者开始对黏弹性管道瞬变流压力波动的影响机制进行了理论和实验研究[5-6],并先后提出并优化了黏弹性管道瞬变流计算模型[7-9],证明了这些模型的准确性。
在黏弹性管道瞬变流模型中,管道本构模型主要采用广义开尔文-福伊特(Kelvin-Voigt,KV)力学模型,该模型中包含蠕变柔量和延迟时间两个参数,蠕变参数对瞬变流压力波动的影响规律分析和参数在本构模型中的选取一直是学者们重点关注的问题所在。Urbanowicz等[10]分析了不同水温下蠕变参数对黏弹性管道瞬变流压力波曲线的影响规律。Javadi等[11]分析了黏弹性管道瞬变流压力波动周期对蠕变参数的敏感性。为探究蠕变参数的校核方法,Covas等[5]利用力学拉伸实验,测得高密度聚乙烯(high denisity polyethylene, HDPE)管道的本构曲线,并将其用于数值模拟,结果表明模拟结果与实验结果偏差较大。Pezzinga[12]和Pan等[13-14]分别应用遗传算法和频域分析方法对黏弹性管道瞬变流模型中的蠕变参数进行校核。但这些参数校核方法存在校核程序复杂,耗时长等问题。
对于管道瞬变流动的研究,前人主要针对单一管材的管道系统,而针对弹性/黏弹性混合管道系统的研究较少。为阐明混合管道的瞬变流压力波动影响规律,Garg等[15]进行了钢管/玻璃纤维塑料混合管道的瞬变流实验,在实验中改变塑料管段长度在整个管道系统中的占比,从而分析混合管道瞬变流压力波动影响规律。Trabelsi等[16]在弹性管道系统上游设置塑料短管,研究塑料短管对水锤抑制作用。但目前还未提出适用于弹性/黏弹性混合管道的高效且准确的参数校核方法。
因此,现搭建弹性/黏弹性混合管道瞬变流实验台,并进行了钢管、钢管/PPR混合管道、钢管/HDPE混合管道的瞬变流实验,分析混合管道瞬变流压力波动的影响机制,阐明了波速和蠕变参数对压力波动的影响规律,进而提出一种简单且准确的混合管道波速和蠕变参数的校核方法,基于实验数据验证该方法的准确性,为工程中混合管道的模拟计算和参数校核提供参考和依据。
1 数学模型及求解方法
1.1 数学模型
经典的弹性管道瞬变流控制方程包括连续性方程和动量方程[17],分别表示为

(1)
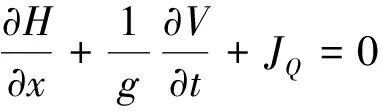
(2)
式中:H为压力水头;V为平均流速;a为波速;g为重力加速度;x为距离;t为时间;JQ为拟稳态摩阻引起的水头损失,可以使用达西-魏斯巴赫(Darcy-Weisbach)公式为
(3)
式(3)中:Q为流量;f为沿程阻力系数;D为管径;A为管道断面截面积。
管道瞬变流压力波的波速a计算公式为
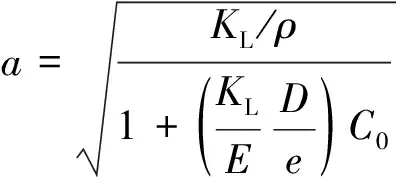
(4)
式(4)中:E为杨氏模量;KL为水的体积模量;ρ为水的密度;e为管道壁厚;C0为约束系数,其计算公式为
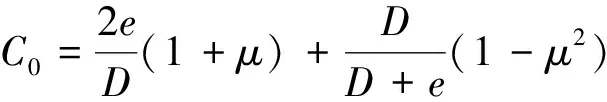
(5)
式(5)中:μ为管道泊松比。
相比弹性管道,黏弹性管道瞬变流控制方程中的连续性方程中增加了延迟应变项,用以模拟管道黏弹性效应,其连续性方程为
(6)
式(6)中:εr为管道的延迟应变。
黏弹性管道的总应变ε为
ε=εe+εr
(7)
式(7)中:εe为黏弹性材料的瞬时应变。
根据玻尔兹曼叠加原理,总应变ε可表示为
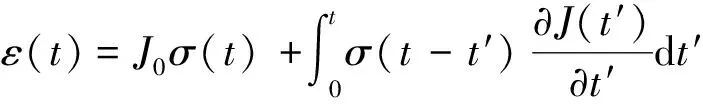
(8)
式(8)中:J0为瞬时蠕变柔量;J(t′)为t′时刻的蠕变柔量;σ(t)为t时刻的应力。
黏弹性材料的蠕变函数使用广义KV模型表式为
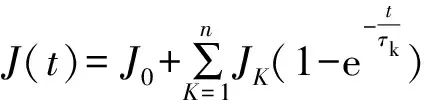
(9)
式(9)中:J0为瞬时蠕变柔量;JK为第K个KV元件的蠕变柔量;τk为延迟时间;n为蠕变元件个数。
1.2 模型求解
(1)弹性管道瞬变流特征线法求解。使用特征线法,将连续性方程[式(1)]和动量方程[式(2)]转化为常微分方程,称之为相容性方程,即
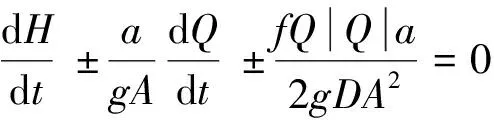
(10)
将式(10)分别沿正负特征线(图1中C+和C-特征线)对相容性方程进行积分,得到代数方程为
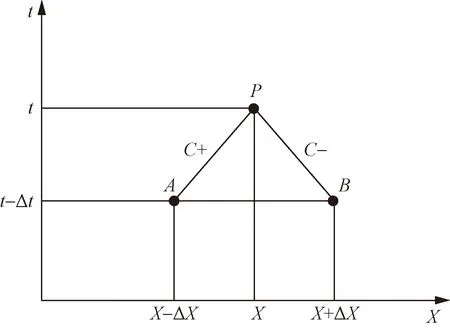
图1 差分网格Fig.1 Grid of characteristics
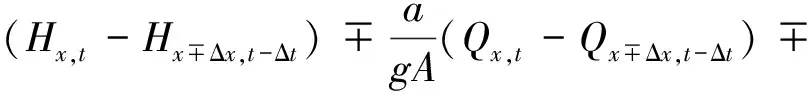
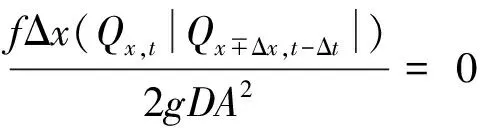
(11)
(2)黏弹性管道瞬变流特征线法求解。使用特征线法,将黏弹性管道连续性方程[式(6)]和动量方程[式(2)]转化为常微分方程,即
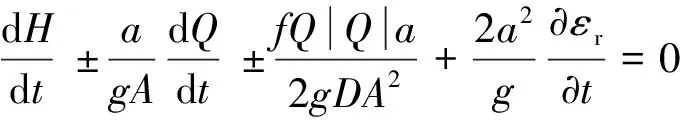
(12)
分别沿正负特征线对方程进行积分,得到代数方程为
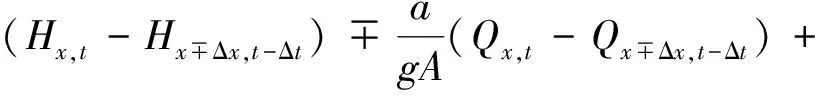
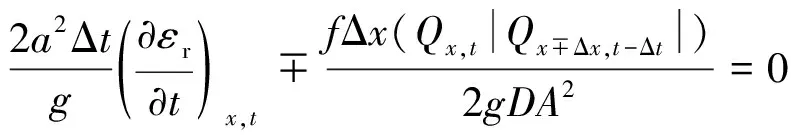
(13)
2 实验装置与结果分析
2.1 实验设备及方法
如图2所示,弹性/黏弹性混合管道瞬变流实验台是由供水水箱、管道、气动阀、替换活接、下游水槽等组成。实验管段为总长为15 m的镀锌钢管,管道的公称直径为DN25、壁厚为3 mm,弹性模量为1.4×1014Pa,泊松比μ为0.23。上游水箱的水位为2.7 m。在管道末端设置气动球阀作为管道瞬变流的激励方式。管道中段两处活接的间距为5.7 m,活接部分管道占整个管道的38%,关阀时间0.15 s,线性关阀,通过实验数据分析和理论计算确定管道沿程阻力系数f为0.036。实验设备的具体型号参数,如表1所示。实验装置的局部实物图如图3所示。

图2 实验装置示意图Fig.2 Schematic diagram of experimental setup

表1 设备及主要参数Table 1 Main parameters of equipment
本次实验分两部分进行,第一部分为弹性管道瞬变流实验,通过关闭管道下游的气动阀门产生管道瞬变流动;第二部分为弹性与黏弹性混合管道瞬变流实验,使用管道中预先设置好的活接,将管道中段钢管替换为高密度聚乙烯(HDPE)和聚丙烯(PPR)管道,从而进行弹性/黏弹性混合管道瞬变流实验,所替换的黏弹性管段的管径和壁厚与弹性管道相同。所进行的实验工况,如表2所示。
本次实验所采用的压力传感器的精度为±0.25% FS,在本实验中测得压力波的峰值为12 m,满度相对误差为1.4%,在可接受的范围内。另外,工况2的水温为24 ℃,其他工况的水温均为15 ℃。

图3 实验装置局部实物图Fig.3 Partial physical picture of experimental device
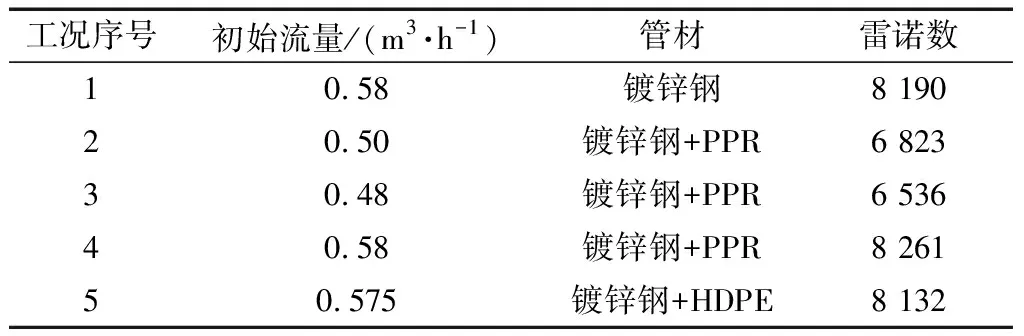
表2 实验工况基本参数Table 2 Parameters of experimental tests
2.2 实验数据分析
对上游水箱作为边界条件、末端关阀作为瞬变流激励方式的实验进行分析。在相同实验参数(表2)下,分别进行镀锌钢管道(工况1)、钢管/PPR管道(工况4)和钢管/HDPE(工况5)管道瞬变流压力波动实验数据,如图4所示。
从图4可见,弹性管道瞬变流压力波的最大波峰值为11.3 m,而钢管/PPR混合管道瞬变流压力波的最大波峰值为10.2 m,钢管/HDPE混合管道瞬变流压力波最大波峰值为8.8 m。与弹性管道瞬变流压力波曲线相比,钢管/PPR混合管道和钢管/HDPE混合管道的压力波最大峰值分别下降9%和22%。另外,在部分管段替换为HDPE管材后,其产生的瞬变流压力波曲线相比弹性管道会出现更加严重的衰减现象,但在替换为PPR管道后衰减幅度与弹性管道相似。但是,钢管/PPR混合管道相比钢管/HDPE混合管道产生了更大的相位延迟现象。

图4 工况1、工况4和工况5的实验数据比较Fig.4 Comparison of experimental data for Cases 1, 4 and 5
3 参数校核方法及验证
提出了一种合理且简便的弹性/黏弹性混合管道瞬变流参数校核方法,并基于不同工况下的实验数据,利用黏弹性管道瞬变流模型验证该校核方法的准确性。对于黏弹性管道,非稳态摩阻对压力波动的影响较小,而黏弹性效应对管道瞬变流压力波动的影响占主导地位[18-19],因此本文研究中将使用黏弹性管道瞬变流模型结合一维拟稳态摩阻模型进行校核。
3.1 弹性管道瞬变流波速校核
以工况1的实验数据为例,对弹性管道瞬变流波速进行校核。通过实验数据计算波速的范围区间,基于实验数据计算波速的方法有以下两种。
(1)在下游气动阀瞬时关闭后,压力波依次通过压力传感器2和压力传感器1,分别记录两传感器首次出现压升的时间、压力首次达到波峰15%的时间、压力首次达到波峰的时间。根据公式a=(L1-L2)/(T1-T2),可计算出压力波波速。
(2)基于压力波每次到达稳态的时间计算出压力波的周期值,根据公式a=4L/T,计算出压力波波速。
应用所述两种方法计算出工况1的波速均为350 m/s左右,考虑到实验数据存在误差,仍需要应用管道瞬变流模型对波速进行进一步校核。
根据式(4)计算弹性管道的瞬变流压力波波速,水体积模量KL取2.1×109Pa、空气体积模量Kg取 1×105Pa、钢管弹性模量E取1.4×1011Pa。泊松比取0.23。根据式(5)计算出约束系数C0为1.17,计算瞬变流波速为1 100 m/s。理论计算结果同实验结果差距过大,推测为管道含气的原因。根据文献[20]中的含气管道波速计算公式,当波速为350 m/s时,管道含气量为0.000 74。
通过实验数据计算出波速为350 m/s后,以实验波速的±5%作为取值范围,通过弹性管道瞬变流模型进一步校核波速。在弹性管道瞬变流动过程中,波速是影响压力波曲线变化的决定性因素,直接影响压力波的周期和首个波峰值。在取值范围内改变波速,找到压力波首个波峰和周期与实验曲线契合程度最好的波速值即为校核结果。波速值为341 m/s为工况1的校核结果,模拟结果如图5所示。结果表明,使用一维拟稳态摩阻模型可以较为准确的模拟出压力波动的峰值和周期情况,但无法准确表达压力波动的衰减情况,这是由于弹性管道的瞬变流压力波动的衰减很大程度上受到非稳态摩阻的影响,而一维拟稳态摩阻模型低估了瞬变流压力波动过程的摩阻耗散[21]。
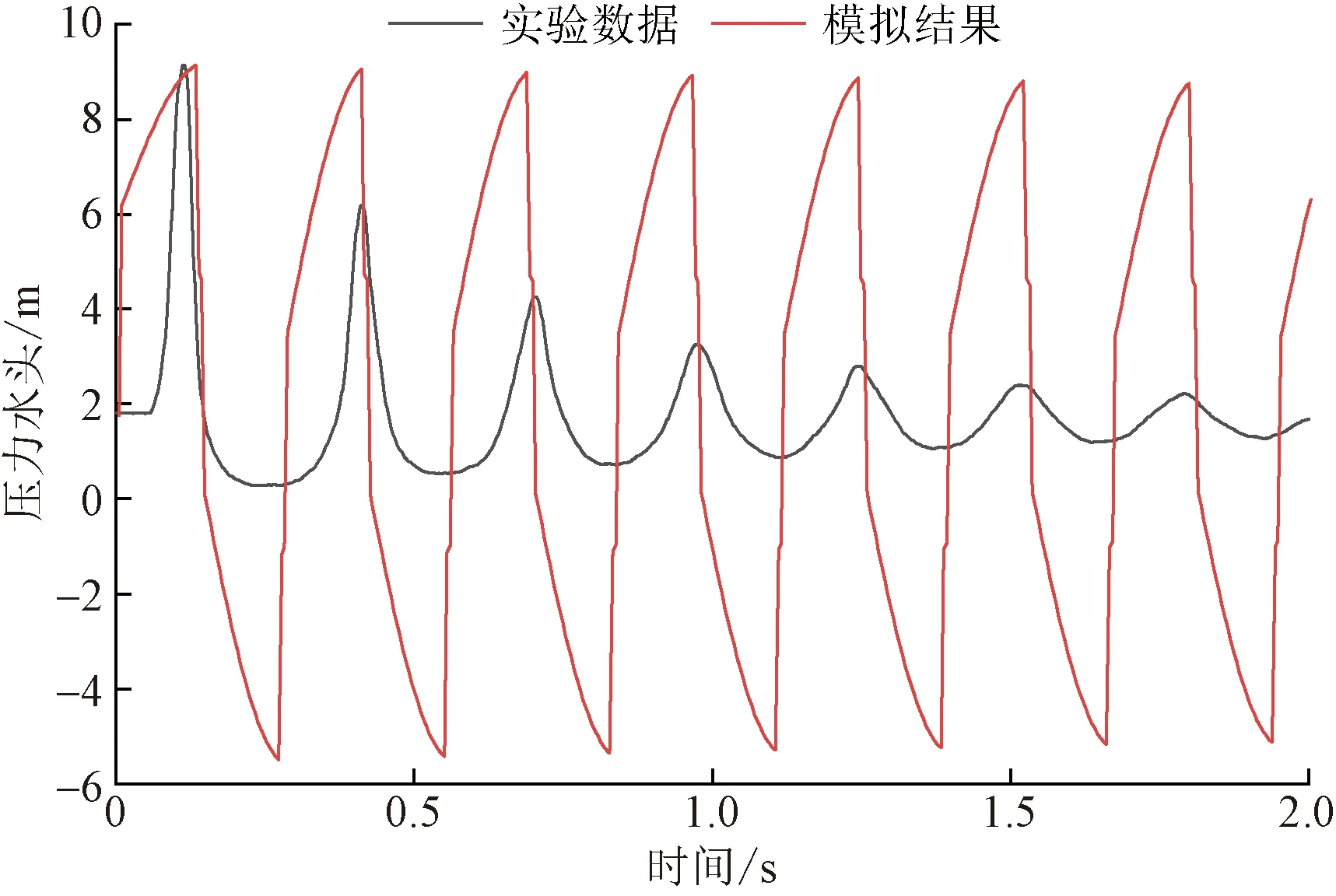
图5 工况1的实验数据及模拟结果对比Fig.5 Comparison of experimental and simulation results in case 1
3.2 混合管道水锤波速校核
用3.1节相同的方法对工况2的实验数据进行计算,计算得出工况2的实验波速的估算值为230 m/s。与弹性管道相同,实验计算波速并非准确的结果,需要应用黏弹性管道瞬变流模型进行进一步校核。
在参数校核的过程中,瞬变流波速大小的影响主要体现在压力波的峰值和周期。但压力波的峰值和周期同时受到波速和蠕变参数的影响,仅仅使用波峰作为波速的校核基准无法得到准确的结果。在瞬变流压力波动过程中前3个周期,管壁的黏弹性对压力波周期的影响较小,可以忽略不计,但在第4个压力波动周期以后,受管壁的黏弹性影响,压力波会产生少量的相位延迟现象。所以,使用压力波动的前3个周期作为基准可以较准确校核出压力波速值。以本实验为例,在黏弹性管道瞬变流模型中选取波速值为251 m/s时,模拟结果的前3个周期与实验曲线的契合程度最高。
3.3 本构参数校核
对于黏弹性管道的数值模拟,仅仅通过波速不能充分模拟出压力波动情况,还需要在本构模型(即KV模型)中确定蠕变参数。并且,由于混合管道中管材占比不同,通过力学实验直接测量管道的蠕变参数的方法是不可行的,只能借助实验数据使用参数校核的方式得到混合管道的蠕变参数。
黏弹性管道本构模型(即KV模型)常用于表达黏弹性管道的蠕变动力学行为。广义的KV模型是多个KV元件组成的,每个KV元件是由一个弹簧和粘壶并联组成的。KV元件的个数影响蠕变曲线的准确性,选择2个及以上的KV元件即可准确模拟出管道的黏弹性行为[22]。蠕变参数的影响体现在压力波的衰减和延迟上。在模型中,蠕变参数由蠕变柔量和延迟时间表达。在参数校核时将延迟时间固定在0.05 s和0.25 s,通过改变蠕变柔量使得模拟曲线接近实验曲线,确定出使模拟结果最接近实验曲线的蠕变参数。
表3列出3组不同大小的蠕变参数,蠕变参数的大小对压力波曲线的影响如图6所示,其中a组的蠕变参数为工况2校核结果,模拟曲线同实验曲线契合程度最高。使用该组蠕变参数以及3.2节校核得出得瞬变流波速进行模拟计算,模拟结果如图7所示。使用黏弹性管道瞬变流模型结合一维拟稳态摩阻模型可以较好地描述黏弹性管道瞬变流压力波动过程,只有第2、3个周期压力波的衰减会有所差异,这是由于在模型中没有考虑非稳态摩阻的影响。

表3 三组蠕变参数Table 3 Three sets of creep parameters for simulation
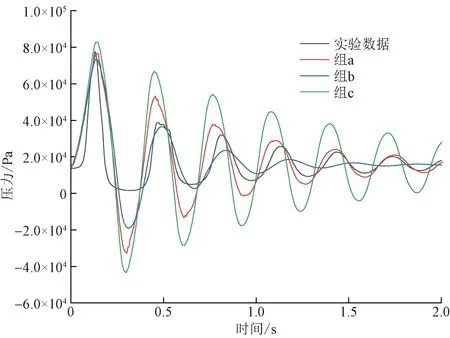
图6 不同蠕变参数下PPR混合管道的模拟结果Fig.6 Simulation results of PPR mixed pipeline under different creep functions
图7 工况2的实验数据及模拟结果对比Fig.7 Comparison of experimental and simulation results in case 2
如图6所示,在延迟时间固定的情况下,b组中使用更大的蠕变参数会导致更大的压力波衰减,使得压力波的过早得趋于平缓,同时相位也会产生更大的延迟现象,c组同理。在校核过程中,第一个波峰值也会在一定程度上受到蠕变参数的影响,尤其在关阀时间较长的系统中,蠕变参数对第一个峰值的影响更为明显。所以,在校核蠕变参数的过程中应综合考虑波峰值、衰减幅度和相位延迟情况。
3.4 不同流量的钢管/PPR混合管道校核模拟
以工况3和工况4的实验数据为基础,对不同流量的工况进行模拟校核并验证不同流量下数学模型的准确性。该两组实验在同温度、同约束条件下进行,工况3、工况4的初始流量分别为0.48、0.58 m3/h。
利用前文所提到的主要参数校核方法,校核得出该两组实验的波速为303 m/s,延迟时间τ1和τ2分别为0.05、0.25 s,蠕变柔量J1和J2分别为0.19×10-9、0.6×10-9Pa-1。工况3和工况4的波速与本构参数同工况2下稍有不同的原因是因为受到了水温等外界条件影响。更高的水温会导致更大的蠕变参数和更小的波速。
使用校核得出的主要参数进行模拟的结果,如图8所示。从图8可知,使用黏弹性管道瞬变流模型结合一维拟稳态摩阻模型可以在一定程度上较准确地模拟出不同初始流量下的混合管道瞬变流压力波动,模拟结果与实验结果产生一定相位偏差是在可接受的范围之内。
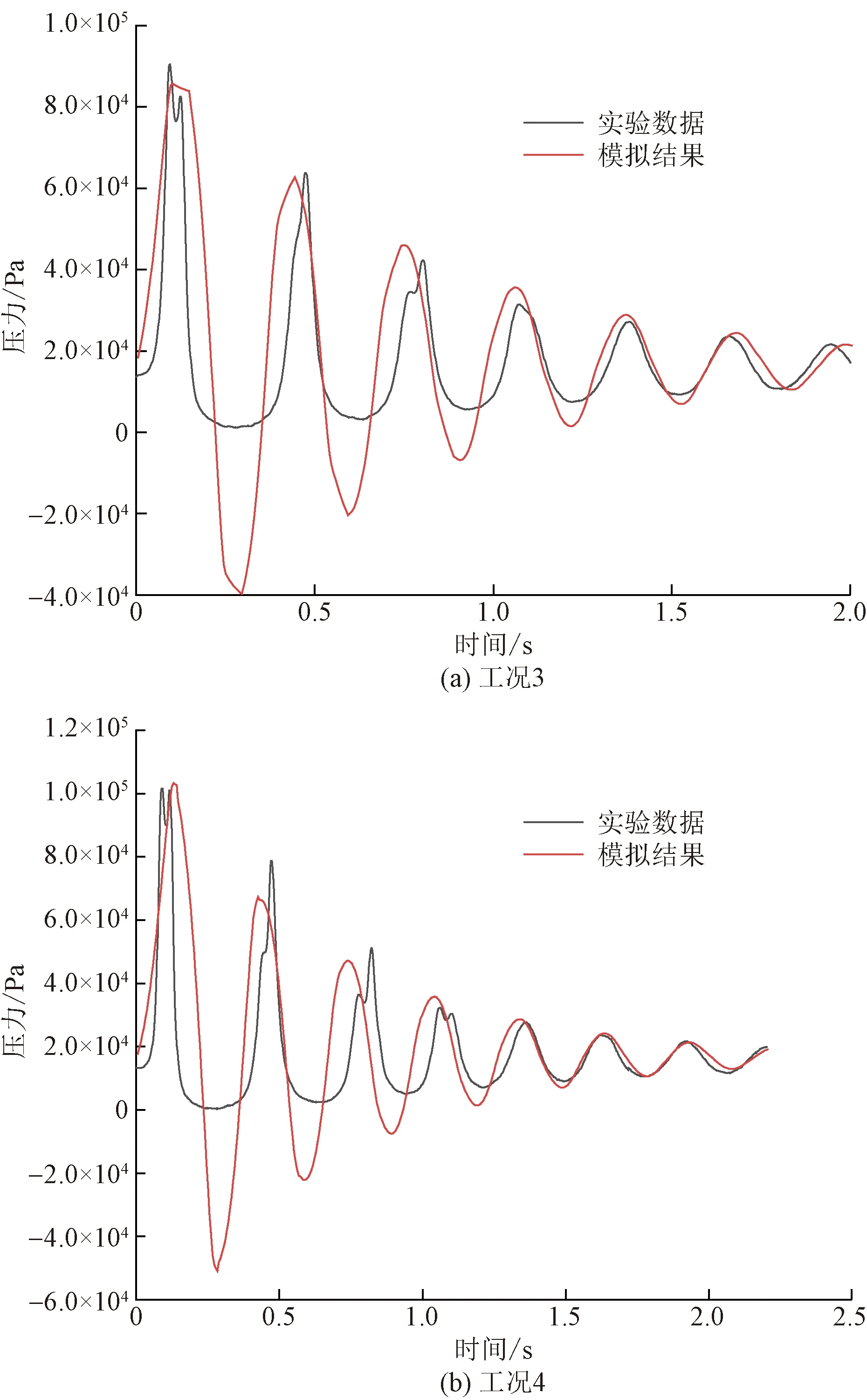
图8 工况3和工况4的实验数据及模拟结果对比Fig.8 Comparison of experimental and simulation results in case 3 and case 4
3.5 钢管/HDPE混合管道的校核模拟
基于工况5的钢管/HDPE混合管道瞬变流实验数据,利用所提到的参数校核方法进行数值模拟。校核得出该工况下的波速为290 m/s、延迟时间τ1和τ2分别为0.05 s和0.5 s,蠕变柔量J1和J2分别为0.13×10-9Pa-1和0.5×10-9Pa-1。模拟结果与实验结果的对比,如图9所示。使用黏弹性管道瞬变流模型结合一维拟稳态摩阻模型可以较准确地模拟出混合管道瞬变流压力波动前期的峰值和衰减情况,误差可以保持在4%以下。但模拟结果与实验结果的相位出现一定程度的偏差,达到10%,在可以接受的范围之内。
4 结论
通过设计并搭建弹性/黏弹性混合管道瞬变流实验台,分别进行了镀锌钢管、钢管/PPR混合管道以及钢管/HDPE混合管道的瞬变流实验,分析弹性/黏弹性混合管道的瞬变流压力波动机制。同时提出了一种简单准确的波速和蠕变参数校核方法,并应用黏弹性管道瞬变流模型结合一维拟稳态摩阻模型对该方法的准确性进行验证。主要得到如下结论。

图9 工况5的实验数据及模拟结果对比Fig.9 Comparison of experimental and simulation results in case 5
(1)在弹性管道系统中部分替换为黏弹性管道可以使得瞬变流压力波波速变小、峰值下降及相位延迟。这一现象在钢管/PPR混合管道中相比钢管/HDPE混合管道更为明显,在本文的实验中,对于黏弹性管道占比为38%的混合管道,钢管/PPR混合管道和钢管/HDPE混合管道的压力波最大峰值分别下降9%和22%。
(2)使用弹性管道一维拟稳态摩阻模型无法准确地模拟出弹性管道瞬变流压力波动衰减情况。但是不同于弹性管道,使用黏弹性管道瞬变流模型结合一维拟稳态摩阻模型可以较准确地对混合管道瞬变流压力波动进行的数值模拟,尽管在衰减和相位上有一定的偏差,但均在可接受的范围之内。
(3)提出了黏弹性管道瞬变流压力波波速和蠕变参数的校核方法。该方法首先通过实验数据计算波速的估算区间。其次,在此区间内以压力波前3个周期为基准,校核出与实验曲线的前3个周期契合程度最高的波速值。最后,以压力波的首个波峰和周期作为基准,校核出与实验曲线的峰值和相位契合度最高的蠕变参数值。

