浸入式边界方法的研究及应用进展

王 卓 杜 林 成 龙 孙晓峰

1 北京航空航天大学航空发动机研究院,北京 100191

2 华为技术有限公司,编译器与编程语言实验室,北京 100094

3 北京航空航天大学能源与动力工程学院,北京 100191

1 概述

计算流体力学(computational fluid dynamics,CFD)通过离散流动控制方程并采用计算机对其进行迭代求解来获得流动的时空特征.流动控制方程通常包含多变量且具有非线性,同时受各种复杂边界条件和初始条件的影响,这导致基于解析推导的传统理论分析手段难以应用,此时CFD 几乎是对流动进行理论分析及预测唯一可用的工具(Goldstine 1980).经过数十年的发展,CFD 目前广泛应用于工业流体领域的分析与设计等环节,这也使得实验环节大幅减少,设计成本得到了有效地降低.

目前绝大多数CFD 方法都是基于结构/非结构化的贴体网格展开,虽然相关的网格生成技术在近几十年来取得了长足的进步(阎超 等 2011),但这一网格形式能够处理的复杂边界问题极其有限,例如对于图1 所示的心脏内的血液流动现象,心脏本身具有复杂的几何外形,且外形随时间呈现出周期性的改变,而采用贴体网格对这一现象进行研究则会面临网格生成及重构困难的挑战.实际上心脏血液流动现象是复杂边界以及运动边界两类问题结合的典型代表,而如何采用CFD 方法对这两类问题进行准确高效的求解也是进一步拓展CFD 方法应用的关键之一.

图1 用于研究心脏血液流动的模型示意图

浸入式边界方法(immersed bundary method,IB method)是一种非常适用于复杂边界及运动边界的CFD 方法,由Peskin (1972,1977)最早提出并且应用于图1 所示的心脏血液流动模拟.IB 方法可以通过在正交的笛卡尔网格上对边界进行建模从而避免对于复杂边界生成贴体网格,在Peskin 所提出的IB 方法中,固壁边界对流动的影响在控制方程中引入相应的力源项来进行刻画,如图2 所示.在边界位置发生改变时,只需要对相应的力源项进行修改即可,因此能够避免对网格进行重构.通过力源项来刻画边界的影响早在20 世纪60 年代就被Sirovich (1967)从理论上证明其数学上的理论可行性,因此这一方法在随后的CFD 发展中获得了巨大的进步,演化出各种不同的版本形式,并且还与基于雷诺平均的湍流数值模拟(RANS)、大涡模拟(LES)以及直接数值模拟(DNS)等各类不同精度的数值模拟技术相结合,被广泛应用于包含复杂边界及运动边界的各类流动问题的研究(Mittal &Iaccarino 2005,Verzicco 2023).

尽管IB 方法在处理复杂边界以及运动边界问题上具有强大的能力,但是其主要缺陷在于处理高雷诺数流动问题时庞大的计算量.由于湍流边界层厚度相较于层流而言非常小,通常需要在壁面处布置高分辨率网格来分辨湍流边界层的线性底层,例如对于Spalart-Allmaras (SA)一方程湍流模型而言(Spalart &Allmaras 1992),通常要求壁面第一层网格的y+小于1.而对于IB 方法来说,由于对笛卡尔的网格加密必须沿空间三个方向同步展开,粗略估计表明,三维情形下网格总量与流动雷诺数的1.5 次方呈正比,而对贴体网格而言仅与雷诺数的0.5 次方呈正比,这也导致对于高雷诺数流动,IB 方法所需的网格量远远超出贴体网格.如何在现有的硬件计算能力基础上拓展IB 方法在高雷诺数流动问题中的应用是进一步扩大该方法的应用范围以及实现工业规模化应用的核心挑战.

本文将首先对IB 方法的基本思想进行介绍,主要关注其中刻画边界影响的力源模型;其次将介绍近年来IB 方法在不同流动问题中的应用,自然界中的生物体绕流通常包含复杂的固壁边界,对其中流动机理的认知将有助于工程领域中设计更高性能的飞行器、推进器等装置;而流固耦合问题则是工程领域典型的一类运动边界问题,由于涉及固体结构的安全而受到密切关注.因此本文将以上述问题作为复杂边界以及运动边界问题的代表来具体介绍IB 方法在相关领域的应用进展.此外,本文还将介绍IB 方法在运动边界发声问题中的研究进展,通常认为IB 方法在边界精度处只有一阶精度,这似乎与计算气动声学中的高精度要求相矛盾,但已有的研究进展表明边界处的计算精度并不会对IB 方法在高精度模拟中的应用产生根本性的阻碍.最后,本文将对IB 方法在高雷诺数流动模拟中的研究进展进行介绍.

2 基本思想

当采用与壁面不贴合的笛卡尔网格进行流动模拟时,一个关键问题是如何刻画壁面边界对于流动的影响,而IB 方法所采取的方式为在控制方程中引入描述边界影响的力源项从而将壁面内部拓展为与外部流场一体化的“伪流场域”.方程(1)给出了适用于不可压缩流动的动量方程,其中u为流动速度,t为时间,p和ρ分别为压力和密度,ν为运动黏度,f(x,t) 即为刻画边界影响的力源项,并且会随时间和空间呈现动态变化.

根据力源建模方式,IB 方法可以进一步细分为连续力源法和离散力源法.

2.1 连续力源法

记xi为壁面拉格朗日坐标系下某一离散边界单元的坐标,Fi为该单元处壁面对流体的作用力,由于方程(1)中的流动控制方程建立于欧拉坐标系,因此f与Fi之间的关系可以写为方程(2)的形式,其中x为欧拉坐标系下的坐标,δ为Dirac Delta 函数.由于δ函数具有奇异性,为提高数值稳定性,在实际处理中通常会采用具有空间连续性以及离散守恒性的正则化函数分布来对其进行代替从而完成对力源的坐标转换(Peskin 1972,Uhlmann 2005),而这一处理方式也导致连续力源法通常在边界处仅有一阶精度.

连续力源法中的另一个关键点在于如何获得壁面与流体之间的作用力Fi.早期Peskin 等人所研究的复杂壁面对象如心脏等一般为弹性体(Peskin 1977,Saiki &Biringen 1996,Uhlmann 2005),对于此种类型的弹性壁面边界可以通过其物质的本构方程来建立壁面内部的弹性力分布,而在壁面处则通过内外部作用力的平衡来间接获得壁面对流体的作用力.这一考虑壁面本构方程的力源方法并不适用于壁面为刚体的情形,因此为了模拟刚体绕流问题,Goldstein 等(1993)通过双模态控制器原理构造了反馈力源方法,其表达式如方程(3)所示,其中ub为壁面处的边界条件.

反馈力源方法实际上是利用线性理论控制流动方程满足壁面边界条件,线性理论能够很好地达到控制效果的原因在于力源作用区域或者控制区域是一个很小的区域,可以近似看成线性区域.Goldstein 等(1993)将该方法用于不可压缩槽道湍流模拟以及圆柱绕流问题,证明了该方法对于非定常流动模拟的精确性,Zhong 和Sun (2009)、Du 等(2016a,2016b)也利用反馈力源法求解不可压缩翼型和叶栅流动,取得了不错的预测结果.反馈力源法的形式极为简单,且为显式力源,可以直接施加到动量方程右端求解.然而反馈力源法中的力源形式涉及两个经验参数(α、β),这两个经验参数用来调节反馈力源的响应速度和对壁面边界条件的满足程度,其取值与具体非定常流动有关.对于定常流动和不同特征频率的非定常流动而言,α、β一般有所不同,但是当其取值过小时,边界处的流动计算精度会有所降低,且收敛较慢,但取值过大又会增加系统刚性,引起数值不稳定.此外,反馈力源法允许的 CFL 数过小 [O(10-3～10-2)] (Goldstein et al.1993,Lee 2003,Shin et al.2008),为此虽然其实现简单,效率极高,但过小的 CFL 数仍然使得其在具体非定常流动计算时允许的时间步长过小.为了进一步放宽CFL 数的限制,Taira 和Colonius (2007),Li 等(2016)以及Wang 等(2020)提出了一种对力源进行隐式求解的投影式IB方法以实现对不可压缩流动的求解.这一方法的核心思想是将力源视作类似于压力项的拉格朗日乘数(Lagrange Multiplier),此时力源项可采用与压力项求解同样的数值思想来获得,从而避免了早期连续力源法中需要人为给定反馈系数的缺陷,同时实现放宽CFL 数限制的目标.

从Goldstein 等(1993)构造的反馈力源形式来看,其流体计算域扩展到了固体内部区域,从而形成了流体计算域和拓展区,拓展区内的流体仍然满足流动控制方程,而力源的强度则同时取决于内外流体的瞬时流动,这种思想的可行性实际上早在 IB 提出之前便已经被Sirovich (1967)证明.该研究推导了可压缩NS 方程的间断形式,此时边界条件完全有间断形式的源项取代,源项的强度则取决于间断强度,即边界内外的应力或热传导等.由此可以看出Sirovich 推导的间断NS 方程以及利用源项代替固体边界条件实际上为Peskin 发展 IB 方法提供了基本理论依据,同时也说明了 IB 方法通过延拓流体域处理刚性固体域的理论可靠性.连续力法通常都只是在浸入式边界点上施加力源,因此物体内部是允许有流动的.从物理上来说,物体内部是固体,是不可能存在流动现象的.但是,对于浸入式边界方法来说,整个域包括固体和流体是一体离散的,控制方程在两个域上没有本质区别,将两个域隔开的界面已经不存在了,起到作用的是“力源”.因此,在算法上是允许内部的虚拟流动的,而且内部流动可以作为外部真实流动的“光顺器”(Goldstein et al.1993).

另外两种典型的连续力源法为虚拟弹簧力源法(Lai &Peskin 2000)和罚函数方法(Kim &Peskin 2007,Huang et al.2011).虚拟弹簧力源法中所构造的力源与流体偏离给定位置的程度成正比,类似于一个具有较大弹性系数的弹簧作用于流体上,当流体稍微偏离预期位置后便会产生极大的回复力将流体“拉”回到固体边界从而使其满足无滑移边界条件,如图3(a)所示.在此基础上Kim 和Peskin 进一步提出罚函数方法,该方法结合虚拟弹簧力和Peskin 早期利用本构方程构建边界力源的方法,将力源分解成无质量边界的弹性力以及由于无质量边界随流体运动后与有质量边界存在位置差异诱导的弹簧力.该方法的优点在于不仅能够考虑无质量固体边界的流固耦合问题,也能够考虑固体边界任意密度分布的流固耦合问题.罚函数方法中力源的给出方式如方程(4)所示,其中Da是达西系数(Darcy number),用以描述多孔介质渗流特性.Da=K0/L2,K0是特征渗透性,L是特征长度.从方程(4)的形式不难看出,这也是一种反馈控制系统,相当于方程(3)中取其中自由参数是K,如果K趋向于无穷,力源项就消失了,主控方程就变成了只作用于纯粹的流体.如果K趋向于零,那么力源项在主控方程中就处于主导地位,其他的诸如对流、扩散、详压力项的值都可以忽略不计.对于多孔介质来说,0＜K＜∞,力源的作用是在指定的区域模拟流体流过时的动量损失,当然,这种情况下主控方程演变为NS/Brinkman 方程.通过调节K的取值,可以将固体壁面、流体、多孔介质一起求解.同样的,K的取值与α和β的问题类似,造成待求解方程的刚性变大,同时受到数值稳定性的限制.

图3 (a) 固壁边界虚拟弹簧力示意图,(b) 锐利界面的浸入式边界方法

2.2 离散力源法

连续力源法虽然形式简单,但是对于不同壁面边界条件的刻画能力比较受限,大部分方法仅仅只能实现简单的不可压缩流动下无滑移壁面边界条件.而离散力源法由于从离散化的 NS 方程出发,因此对于边界条件的刻画更为灵活,其中最具代表性的是由(Mohd Yusof 1997)所发展的方法: 将方程(2)写成如方程(5)所示的离散形式,其中Rn+1/2为方程(2)中除力源项之外的所有右端项.

Lima E Silva 等(2003)形象地将其发展的离散力法叫做“physical virtual model (PVM)”,该离散力源法将力源拆分成四项,分别叫做加速度力、惯性力、黏性力以及压力.在离散力法中,力源是在方程离散后加入到方程中,方程求解稳定性较好,适合于高雷诺数计算,并且可以根据壁面边界条件的不同构造不同的插值方法,由此适用的壁面边界条件更加广泛.Fadlun 等(2000)证明如方程(5)所示的离散力源法能够在边界处实现二阶精度,并且可以与大涡模拟方法相结合,大大地拓宽了IB 方法的适用性.Mohd Yusof (1997)构造的离散力源法需要对壁面位置进行判断和插值操作,判断笛卡尔网格单元与壁面的内外关系.为此Su 等(2007)利用离散力源法和预测-校正算法思想构造出了既不显含经验参数,也不需要专门判断固体边界内外,同时理论上可以精确满足壁面边界条件的离散力源法,并通过静止/运动圆柱绕流问题证明了该方法的时间精确性,数值测试表明该方法相较于连续力源法能够实现较大的 CFL 数 [O(10-1～1)],但需要求解一个与力源相关的线性方程组.基于预测-校正的思想,Wu 和Shu (2009)提出了一种与格子玻尔兹曼方法相结合的IB 方法,其中力源项通过隐式速度修正的方式来构建,文中采用圆柱及翼型绕流等案例验证该方法的精度.Yang 等(2017)进一步将该方法与Yang 等(2015,2016)所发展的多种通量计算格式相结合并应用于多种不同类型的三维可压缩/不可压缩的流动计算中.Wang 和Zhang (2011)发展了适用于离散流函数(discrete stream function)方法的IB 方法,并采用多个不可压缩的静止/运动边界案例对算法进行验证,Wang 和Zhang (2011)还结合了局部网格加密的技术来降低网格总量从而提升计算效率,这一网格处理方式也是目前采用IB方法模拟高雷诺数流动常用网格技术.

在离散力源法思想的指导下,实际上后来发展了无需力源的浸入式边界方法,主要代表为混合笛卡尔/浸入式边界方法(hybrid cartesian/immersed boundary method) (Gilmanov et al.2003,Gilmanov &Sotiropoulos 2005)和鬼点法(ghost-cell method)(Tseng &Ferziger 2003,Mittal et al.2008,Lee &You 2013,Zhang et al.2021)等.这类方法通常又被称之为锐利界面的IB 方法.在该类方法中,通常需要为每个边界外部的流场单元沿壁面外法向构造外力点(forcing point),在鬼点法中又被称之为镜像点(image point),如图3(b)所示,其中的P1即为网格点P0所对应的外力点,外力点处的流动变量一般通过插值获得,进一步可在壁面附近构造出满足壁面边界条件的流动时空分布,并代入离散的流动控制方程中进行求解,以此刻画壁面边界对流场的影响.值得注意的是,Tseng 和Ferziger (2003)所提出的鬼点法仍然采用的是早期离散力源法的思想,即构建鬼点的目的是计算力源分布,因此与其他类型的鬼点法有着显著的差异.从上述过程来看,锐利界面的IB 方法拥有与贴体网格方法相似的边界刻画思想,但由于网格点并未与壁面完全贴合,这一类方法通常在壁面处并不能满足守恒性,因此在处理运动边界问题时,壁面处会出现不同程度的数值振荡(Lee &You 2013,Al-Marouf &Samtaney 2017,Griffith &Leontini 2017).相较于连续力源法,离散力源法中需要判断每个笛卡尔网格单元位于固体内部还是外部,并且对于近壁面的网格单元还需要精确计算其到固体边界的距离,该距离在运动边界问题的模拟中需要根据固体边界位置实时更新,可能消耗额外的计算资源,同时该参数也是湍流模拟所必须知晓的一个网格参数,而连续力源法的施加中并不会对这一距离进行计算.因此从这一角度看,离散力源法可能比连续力源法更加适合用于湍流模拟,而目前已公开发表的关于IB 方法在湍流模拟中应用的文章,全部采用的是离散力源法(Capizzano 2011,2016,Tamaki et al.2017,Wang 等2023),下文章节将进一步的讨论IB 方法在湍流模拟中的应用.

3 IB 方法在运动边界问题中的应用

3.1 生物流动

自然界中的鱼类、鸟类等生物均依靠自身部位 (鱼鳍和鸟的翅膀) 在流体介质中的摆动来获得前进的动力(Tong et al.2021,Zhang et al.2022a),这一过程通常表现出较高的推进效率以及较低的噪声水平.因此人类始终希望能够深入理解自然界生物流动中的复杂机理,以此来设计具有更高性能的推进装置,CFD 方法是目前广泛采用的一种研究手段.

以鱼鳍为例,真实的鱼鳍通常具有复杂的外形,单个鱼鳍在摆动过程中的推力状态可能与鱼的身体或上下游的其他鳍的摆动相互耦合(Park &Sung 2018,Han et al.2020,Mendelson &Techet 2021).与此同时,由于某些鱼类经常组成庞大的群体,这种群体行为同样会对单个个体的推力状态以及流场结构产生重要的影响(Weihs 1973,Gazzola et al.2016,Bao et al.2017).这些基本特征使得传统的贴体网格方法在处理这一类问题上面临网格生成困难、多体运动问题难以处理的挑战,而这些挑战正是IB 方法所擅长之处,因此这一方法也在鱼类游泳等生物流动领域获得了广泛的应用.

为降低预测难度同时把握关键物理因素,早期对于生物流动的数值模拟研究多采用简化固体模型,如用振动翼型来表示鱼鳍或鸟翅(Wang et al.2014,2019,Deng &Caulfield 2015,Deng et al.2015,2016).而近年来的部分研究工作已经开始将生物体真实几何外形以及摆动规律包含于数值模拟中.图4(a)给出了一种外形类似蝙蝠的鱼类示意图,对于蝙蝠鱼而言,其推力产生机制难以通过简化的固体模型进行阐述,因此Huang 等(2020)通过对真实蝙蝠鱼身体摆动规律的细致观察建立了如图4(b)所示的固体模型,其中鱼身的摆动通过指定固体边界在不同时刻的空间分布来实现.Zhang 等(2022a)采用IB 方法对图4(b)中的蝙蝠鱼模型的推力产生机制展开了系统性的参数研究,其结果表明鱼身沿弦向(或流向)的摆动波长对于推力的产生、推进效率以及能量消耗等参数有着至关重要的影响,合适的弦向摆动波长有助于获得更高的推进性能,而摆动频率同样能够对于前缘涡、翼尖涡等涡系结构产生明显的影响进而改变推进状态.上述研究结果对于深入理解包含复杂三维变形鱼类的推力产生机理具有重要意义,而这一问题对于采用贴体网格的CFD 方法而言具有极大的挑战性.

图4 蝙蝠鱼示意图(Huang et al.2020,Zhang et al.2022b)

正如前文所提到,鱼类在游泳的过程中多个鳍之间的流动结构会产生相互干涉进而影响推力状态,贴体网格在处理多鳍干涉问题时往往面临不同程度的网格重构困难,通常来讲运动边界的数量越多重构过程越复杂,重构过程消耗的计算资源也会越多.而对于IB 方法而言,由于采用固定的笛卡尔网格,运动边界的数量并不会对数值模拟的过程产生根本性的影响,因此在处理此类多运动边界问题上IB 方法同样具有明显的优势(Pan et al.2016).金枪鱼、鳟鱼等是典型的依靠多鳍干涉产生推力的鱼类,其中主要包含腹鳍、臀鳍以及尾鳍等之间的相互干涉,Zhang 等(2022b)采用IB 方法对金枪鱼中腹鳍与尾鳍之间的相互干涉及推力产生机理进行了数值模拟研究,结果表明在腹鳍尾迹的激励下,尾鳍所产生的推力能够出现明显提高,但腹鳍的推力状态基本不受尾鳍的影响,其主要作用机理在于尾鳍所产生的前缘脱落涡强度会在于腹鳍尾迹中脱落涡的融合过程中被强化,这种鱼鳍间的非定常尾迹相互作用机制在鱼鳍间距较大时会表现得更加稳定.鱼类群体游泳现象与单个鱼的多鳍问题是相似的,本质上也属于多运动边界问题,Peng等(2018)、Kelly 和Menzer (2023)均采用IB 方法对鱼类群体游泳现象中的非定常涡相互作用机制及其对推力的影响进行了深入研究,其中均使用多个运动边界来对鱼群进行模拟,不同个体的尾迹之间相互干涉所形成的流动特征如图5 所示.上述研究也充分体现了IB 方法在处理运动边界问题上的优势.由于本文主要关注数值计算方法而非物理机理,因此仅列举部分IB 方法应用的案例,详细的物理机理读者可参考Zhang 等(2022a)所撰写的文章.

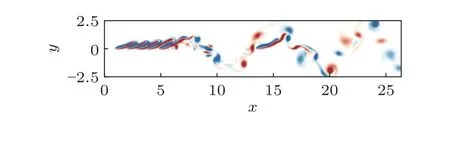
图5 鱼类群体游泳数值模拟中不同个体的尾迹互相干涉(Peng et al.2018)

3.2 流固耦合

流固耦合现象是工程领域备受关注的问题之一,因为固体结构的振动可能会导致其产生严重的破坏失效进而对生命财产安全带来巨大的损失,一个典型案例是1940 年美国Tacoma 大桥在低速自然风的激励下出现剧烈振动进而导致桥梁整体坍塌.流固耦合问题同样是一类常见的运动边界问题,上节所提到的生物流动问题中,边界的运动轨迹主要是通过外部输入的运动规律进行控制,而对于流固耦合问题,固体边界的运动则是由流场激励以及固体结构响应共同决定的.因此当采用贴体网格求解时,由于固体运动规律未知,对于网格重构算法的要求也会相对更高.对于具有复杂边界或者包含多物体的流固耦合问题,应用IB 方法同样具有可以通过采用正交的笛卡尔网格以及避免由于边界运动所引起的网格重构来降低计算模型的复杂程度.

圆柱、方柱等钝体的涡致振动(vortex-induced vibration,VIV)是自然界中最为基本的一类流固耦合问题,因为这一类问题通常具有相对简单的固体几何,对应的流动结构特征更加明显,有助于准确地把握流固耦合现象背后的主要物理规律.Griffith 和Leontini (2017)提出了一种锐利界面的IB 方法并成功将其应用于VIV 问题,Du 等(2014)、Du 和Sun (2015)将Gilmanov 等(2003)、Gilmanov 和Sotiropoulos (2005)所提出的一种锐利界面IB 方法进一步拓展至可压缩流动并利用该方法研究了圆柱VIV 中非定常涡结构的三维特征,同时证明圆柱旋转对VIV 的抑制作用,该抑制作用被(Wong et al.2018)的实验研究所验证.Chen 等(2018)进一步采用IB 方法研究了三个串列圆柱的流致振动问题,深入分析了圆柱之间距离对其流固耦合效应的影响.Xie等(2019)采用一种基于罚函数的IB 方法对圆柱VIV 进行了数值模拟研究,主要关注附着于圆柱后端的柔性细丝对圆柱VIV 响应的影响,结果表明柔性细丝会加剧圆柱VIV 的共振幅值,并且会拓宽出现VIV 锁定的频率范围.总体来看,目前IB 方法在VIV 等钝体流固耦合问题上的应用已经比较成熟,相关的研究极大促进了研究人员对这一现象的物理理解,特别是包含多个钝体的情形.

上文中提到桥梁因受自然风而产生振动变形是建筑领域中一个重要的流固耦合问题,而桥梁本身结构复杂,包含主梁、栏杆以及悬索等众多组成部分,每个部分均可能在风中产生非定常脱落涡,进而对桥梁造成激励导致其出现流固耦合振动.Wang 和Cao (2022)采用IB 方法对主梁上的多条栏杆进行了建模,并将其与完全采用贴体非结构网格的方式进行了比对,结果显示在主梁的基础上采用IB 方法来刻画侧部栏杆能够大幅降低网格的复杂程度.Zhao 等(2020)采用IB 方法对桥梁甲板与桥墩的组合模型进行了数值模拟,主要关注在飓风、海啸等极端条件下桥梁的流固耦合响应,数值模拟准确地预测实验结果,并且表明水面波动所产生垂直于桥梁甲板方向的作用力是相邻桥墩之间甲板上激励的主要来源.上述研究结果共同表明,对于桥梁这一类包含多个不同组件的系统而言,IB 方法能够有效地降低预测其流固耦合响应的难度.

航空领域的叶轮机械叶片颤振是一类典型的包含多运动边界的流固耦合问题,而目前在对这一现象进行预测的时候,多采用能量法对问题进行简化,即假定叶片以某一固有特征频率做小幅振动,通过一个振动周期内流体对叶片做的功来判断叶片是否稳定,即振幅是否会被放大.能量法的假设并不能够准确描述这一真实的流固耦合过程,因此对于同一问题,不同的预测代码之间往往表现出较大的误差(Holzinger et al.2016),但是对包含多叶片的流固耦合问题进行模拟往往又因为网格重构等过程需要消耗巨大的计算量.为此,Zhong 和Sun (2009)将IB 方法应用于叶轮机械叶片颤振问题的模拟预测中,大大降低了考虑多叶片流固耦合计算模型的网格复杂程度,同时能够准确地捕捉到由于非线性作用所引起的振动极限环.Zhong 和Sun (2009)的工作还是在层流条件下开展了,而实际叶轮机械流动通常具有较高的雷诺数,因此Du 等(2016a,2016b)进一步将IB 方法拓展至高雷诺数并对包含多排叶片的情形展开了数值模拟,深入阐述了由多叶片排干涉所引起的非定常效应对叶片负荷的影响,其中计算模型及所得到的流场云图分布如图6 所示.Du 等人的研究表明,采用IB 方法可以克服传统贴体网格方法在处理小轴向间距叶片排问题上所面临的网格生成困难等难题.上述研究工作对高雷诺数流动的模拟以及IB 方法的工程应用进行了初步的尝试,其结果表明对于工程领域的高雷诺数流动,由于需要布置大量的网格对流动边界层进行分辨,在严格满足湍流模型要求的网格分辨率下,IB 方法所需的网格量通常会远超传统贴体网格,因此有必要对方法进行进一步改进以实现更加高效的预测.

图6 基于IB 方法的叶轮机械转静干涉计算.(a) 转静叶片排模型,(b) 流场瞬时涡量分布(Du et al,2016a,2016b)

除了上述工程问题的应用研究以外,自然界还存在许多其他的流固耦合现象,IB 方法也在其机理研究中扮演着重要的角色.例如Huang 等(2007)提出了一种适用于细丝摆动[图7(a)]的IB 方法,通过构建力源的方式来描述能够产生柔性变形的细丝对流场的影响,进而耦合控制细丝运动的结构方程来对二维流场中细丝的流固耦合响应进行求解,Jia 等(2007)、Kim 等(2010)、Uddin 等(2015)都对两个细丝串列组合的情形进行了数值模拟研究,并对其中流动模态的耦合特征进行了深入分析.细丝的流固耦合摆动问题是实际生活中旗子迎风飘扬等物理现象的简化模型,而这类现象通常具有较强的三维效应,因此Huang 和Sung (2010)进一步采用IB方法对一个三维旗子模型的流固耦合响应问题进行了数值模拟研究,阐明了流动雷诺数对旗子摆动模态的影响以及相应的三维非定常涡结构.通过三维模拟作者发现,某些特征涡结构能够通过降低旗子两侧的压差来提升旗子的稳定性,降低摆动强度.Ni 等(2023)将Huang 等(2007)中的细丝闭合成一环形并将局部固定从而组成一刚体与柔性体组合的固壁边界,如图7(b)所示,通过IB 方法求解了柔性体部分的弹性变形,结果表明通过改变柔性体的长度可以实现对其流固耦合运动模态的控制，如图8 所示.Deng 等(2019)采用IB 方法对附着于圆柱的柔性细丝进行了数值模拟,结果表明细丝的摆动能够有效地降低圆柱的阻力以及升力系数的波动.

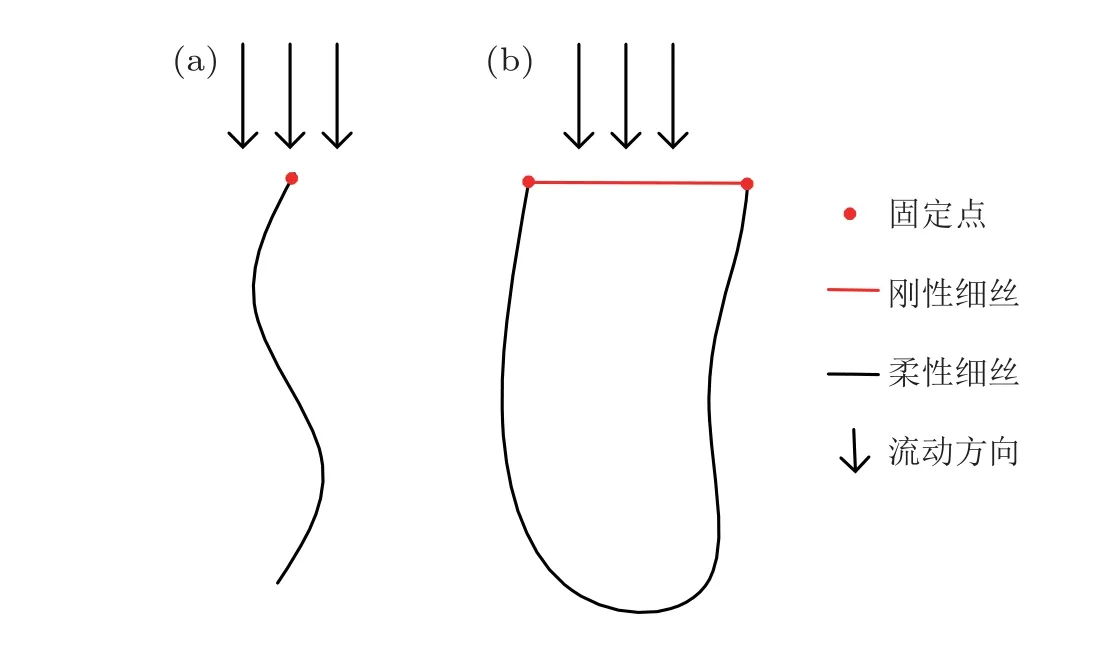
图7 (a) 二维柔性细丝示意图,(b) 刚性/柔性细丝组合体

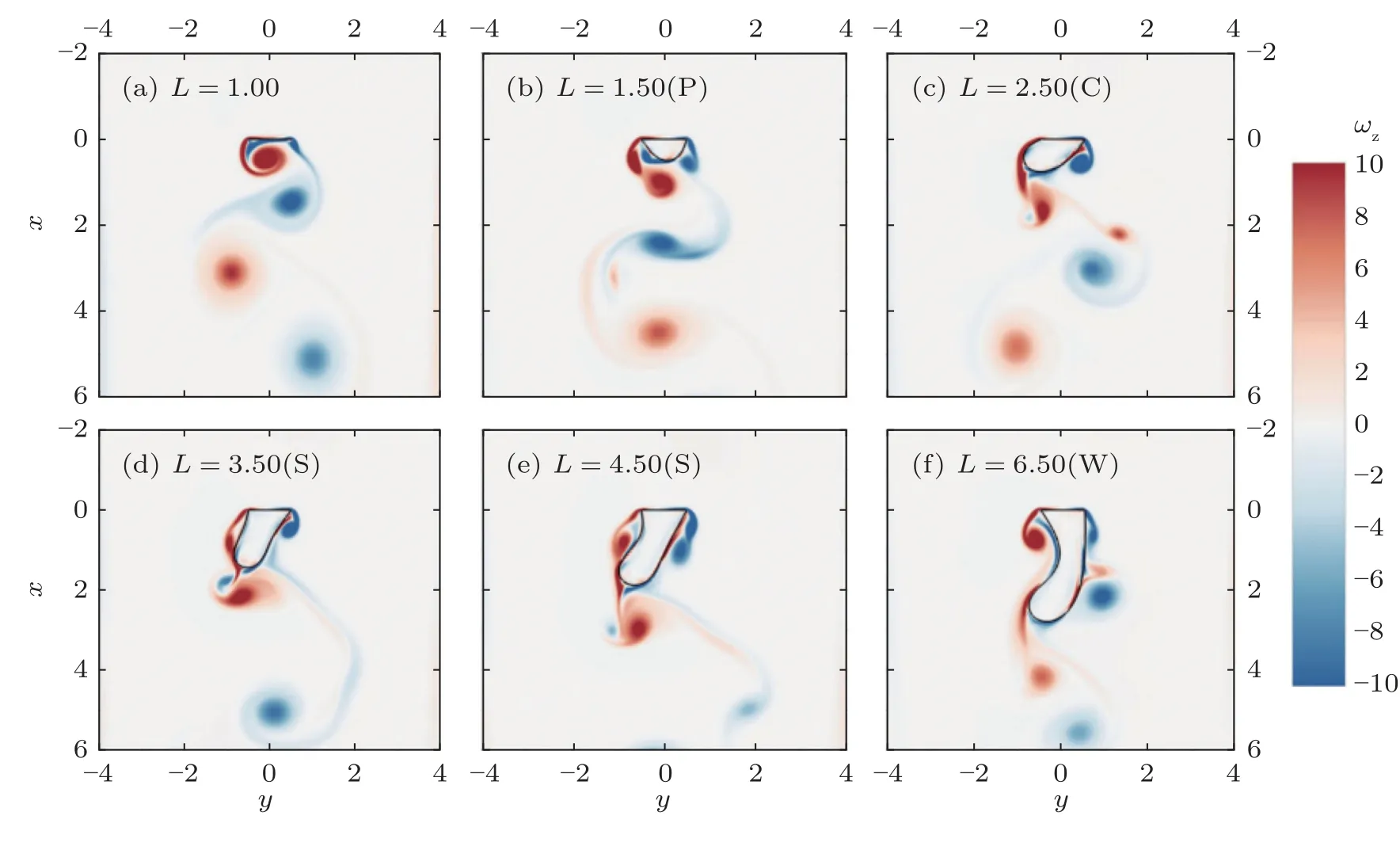
图8 长度对刚性/柔性细丝组合体流固耦合响应及尾迹的影响(Ni et al.2023)

从上述研究工作中不难发现,采用IB 方法能够大幅简化包含多个运动边界流固耦合问题的网格复杂程度,特别是对于边界外形复杂的情形,IB 方法中高质量的笛卡尔网格以及无需网格重构特点相较于传统贴体网格方法而言,优势更加明显.

3.3 运动边界发声

发展现代高阶CFD/CAA 方法是处理运动边界复杂流动发声问题的主要途径之一(Wang et al.2013,Slotnick et al.2014),但基于贴体网格的高阶 CFD/CAA 方法处理涉及流-固-声多物理场耦合的流致发声问题时一般存在网格重构质量和效率相互矛盾的局限性.为了突破这种局限性,极有希望的解决思路是利用 IB 方法构造适合高阶 CFD/CAA 方法的可压缩体积力模型.

事实上,高阶 CFD/CAA 方法结合 IB 方法的思路早在2011 年就已经被Seo 和Mittal(2011)提出并尝试进行静止物体绕流的直接噪声模拟 (direct noise computation,DNC),从而实现流场声场一体解.Mittal 等(2008)直接改进了不可压缩流动下的鬼点 IB 方法,未引入体积力模型,通过构造高阶插值方法满足壁面边界条件,并保持了流固界面尖锐的性质.然而,不同于传统低阶 CFD 方法,高阶 CFD/CAA 方法中的鬼点法必须采用足够多的网格点构造高阶插值,使得靠近壁面处笛卡尔网格上的流动计算必须采用高度非对称或者偏侧形式的空间离散格式以及滤波或者人工黏性模板,这使得靠近壁面处的网格性质同样高度各向异性.当处理不规则几何边界时,这种各向异性极易激发起数值伪波,不仅会使流场及声场数值解降阶,也极有可能产生数值不稳定性现象.这种由于偏侧格式的使用造成声场解降阶的现象也在Kurbatskii和Tam (1997)关于笛卡尔网格下涉及曲线边界时使用偏侧耗散关系保持(dispersion relation preserving,DRP)格式时所发现,并且根据Trefethen (1982)的理论探讨,发现这种现象在频散性有限差分方法中是广泛存在的.Trefethen 通过分析二维有限差分方法的群速度揭示了对于波的传播问题,任何各项异性如非对称模板数值格式、不均匀介质或者计算网格等均可能导致杂波或者也称为寄生波 (parasite waves) 的激发.而无论是对于锐利界面IB 方法(Seo &Mittal 2011)还是Kurbatskii 和Tam (1997)针对 CAA 发展的笛卡尔方法,虽然其采用的笛卡尔网格能够最大程度上保持各项同性,但由于数值格式模板的非对称性总会导致不同强度的寄生波,这对于运动边界发声问题模拟的影响难以评估.据此不难发现对于涉及声学问题的模拟,尽量避免各项异性对数值准确性和稳定性可能具有显著好处.

从Sirovich (1967)的流场延拓理论以及Peskin (1972,1977)所提出的体积力方法不难看出,Gilmanov 等(2003)、Gilmanov 和Sotiropoulos (2005)、Mittal 等(2008)、Seo 和Mittal (2011)等研究所采用的锐利界面IB 方法实际上已经放弃了Peskin 所提出的流体域延拓以及原始体积力思想,这直接导致了壁面附近网格上流体计算必须采用非对称数值格式的结果,这也是CAA 计算中所希望避免的.对比之下,Liu 和Vasilyev (2007)、Sun 等(2012)、Cheng 等(2018,2021b)的工作大致遵循 Peskin 所提出IB 方法中连续力源的基本思想,将固体域视为流体延拓后的伪流体域统一考虑,并分别针对高阶 CAA 方法发展了Brinkman 罚函数 IB 方法以及基于Su 等(2007)的半隐式 IB 方法发展了影响矩阵法 (influence matrix method,IMM).由于体积力模型的采用,在流固界面附近可以采用统一的高阶中心差分格式求解.之后,Komatsu 等(2016)分析发现Liu &Vasilyev (2007)的罚函数 IB 方法不满足伽利略不变性,从而不适用于运动边界问题模拟,为此他们修正了能量方程中的源项模型,使之能够考虑运动边界发声问题,如振荡圆柱直接噪声模拟.但根据罚函数方法的构造原理,可以发现其仍然存在如下缺点: (1) 需要进行内外流场判断,对于三维复杂几何边界问题非常耗时;(2) Mask 函数的采用使得跨越流固界面时体积力存在跳变;(3) 流固边界被修改为阶梯形,导致壁面边界条件不能准确施加在流固边界;(4) 无法定义流固界面法线,因此不能处理无黏问题中的无穿透壁面边界条件.

相比之下,Sun 等(2012)、Cheng 等(2018,2021b)发展的 IMM 方法具有一定优势,其体积力模型和原始 IB 方法一样通过一个近似 Dirac 函数分布到流固界面周围,因此不需要区分流固界面内外流场,并且壁面边界条件可以精确施加在流固界面处,不需要修改边界形状,也可以处理无黏流动问题.Sun 等(2012)利用IMM 方法对复杂边界的声散射问题进行了数值模拟,声场结果如图9 所示,通过将数值结果与解析解进行对比来对方法的性能进行评估,结果表明IMM方法能够对复杂边界的声散射问题进行准确模拟并获得与解析解一致的结果.然而,Sun 等(2012)、Cheng 等(2018)的工作主要针对均匀背景流动下的线性声散射问题,求解线化 Euler 方程,其局限性在于忽略了背景流动、非线性以及流体与声学相互作用,且其采用的奇异值分解方法 (singular value decomposition,SVD) 求解力源方程组耗时巨大,难以处理复杂运动边界发声问题.除此之外,其局限性还体现在方法的收敛性上,和一般贴体网格方法不同,IMM 由于涉及边界网格和笛卡尔背景网格,其求解的体积力收敛性以及稳定性该如何定义仍然模糊不清.这些问题直接影响其是否能够应用到实际复杂运动边界发声的多物理场耦合问题.

图9 多个圆柱散射下的声场压力分布(Sun et al.2012)

在IMM 方法的基础上,Cheng 等(2021b)利用预测-校正思想进一步推导了非线性主控方程下的可压缩体积力模型,并且通过分析体积力模型的物理意义构造模型方程实现该类方法的收敛性和稳定性分析,从而据此开发了鲁棒性更强的快速求解算法.由于流场外内是采用统一的插值模板进行求解,因此边界处不存在由于采用偏侧差分格式所引起的数值伪波,数值稳定性明显提高.利用上述算法,Cheng 等(2021a)研究了二维叶栅非定常流动中振动诱发声共振问题的物理机制,揭示了声共振工况下叶栅流场分布特征,如图10 所示.上述基于IB 方法的CAA 算法还被应用于更加复杂的三维运动边界流致发声问题,例如开式转子噪声的产生及传播,如图11所示,上述结果对于理解气动噪声背后的流动机理具有重要的工程价值.

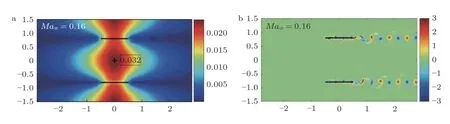
图10 叶栅声共振所对应的流场特征.(a) 压力云图,(b) 涡量云图(Cheng et al.2021a)

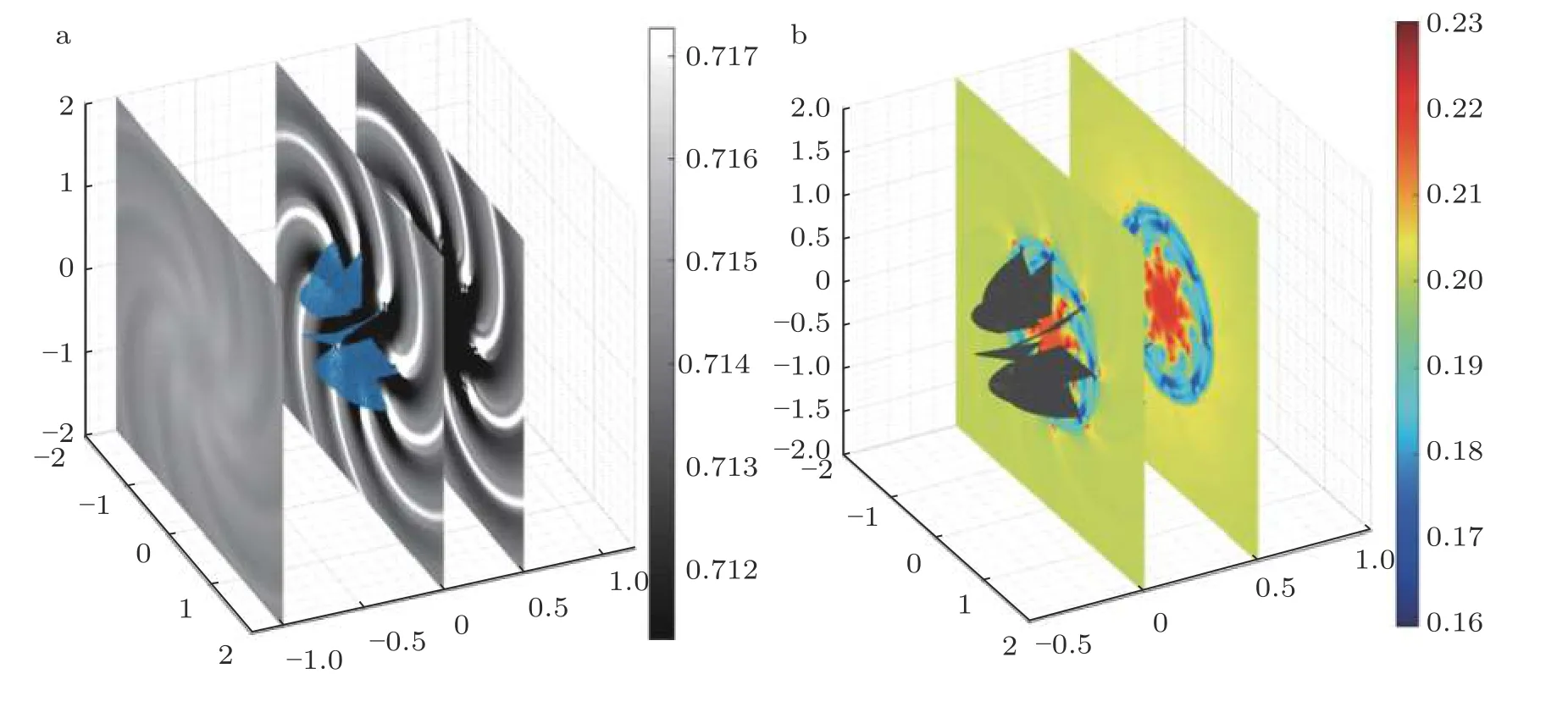
图11 开式转子流致发声直接数值模拟结果.(a) 瞬时压力纹影图,(b) 马赫数云图分布

采用IB 方法进行CAA 计算的一个关键问题仍然在于边界处的处理精度,上文中提到,在连续力源法中采用连续分布的函数来代替Dirac 函数导致边界处通常只能达到一阶精度,这与CAA 计算中追求的高阶精度是相矛盾的,但是从Sun 等(2012)、Cheng 等(2018,2021a)的研究结果来看,边界处的一阶精度似乎并不会对声学模拟的总体准确性产生特别大的影响,但是进一步提高边界处的处理精度始终是研究IB 方法所追求的目标之一.Liang 等(2008) 针对间断问题的数值振荡现象,提出了一种对间断函数的全局描述思想,将间断函数表示为光滑函数和修正项之和,其中修正项由间断处的跃度条件确定,通过这样的转换,在求解微分方程时,一个存在间断的问题可以转换为光滑问题,进一步可将谱方法应用于间断问题而不会带来Gibbs 振荡,其数值结果表明,采用此种求解方式可有效提高边界处的求解精度,精度阶数与所构造的阶跃条件密切相关.这本质上属于一种浸入式界面方法(immersed interface method,IIM) (LeVeque &Li 1994,Xu &Wang 2006a,2006b,Zhong 2007,Gabbard 等 2022),虽然能够有效地提高间断处理精度,但是阶跃条件的复杂程度以及相应的计算量都会随精度的提升而大幅提高,如何进一步提高其数值稳定性并拓展其在CAA 中的应用仍有待进一步研究.

4 高雷诺数流动模拟

4.1 实现高雷诺数流动模拟的途径

虽然IB 方法在运动边界及复杂边界流动模拟等问题上展现出了极大的优势,但是其主要劣势在于高雷诺数流动模拟时庞大的计算量,这一点也直接导致该方法目前在实际工程领域难以广泛应用.在低雷诺数层流条件下,笛卡尔网格所需的单元总量与贴体网格的差异并不明显,但是在高雷诺数条件下,倘若笛卡尔网格与贴体网格同样满足边界层分辨率的要求,那么笛卡尔网格所需的单元总量会远远超出贴体网格,二维及三维情形下,二者网格总量的比值大约分别与雷诺数及其 1.5 次方呈正比(Mittal &Iaccarino 2005),因此高雷诺数流动模拟对于浸入式边界方法来说是一个巨大的挑战.

采用自适应网格加密 (adaptive mesh refinement,AMR) 方式是减少湍流模拟时网格量的主要方法,这一方法可以直接对目标区域进行局部加密从而避免传统拉伸网格方式引起的远场网格总量上升,如图12 所示.Berger 和Oliger(1984)、Berger 和Colella(1989)曾采用自适应加密的方式来提升网格在激波间断处的流场分辨率并说明这一方式可以高效地实现局部网格密度的提升,适合用于准确描述流场中存在高梯度的区域.同时,Roma 等(1999)、De Tullio 等(2007)、Angelidis 等(2016)、Al-Marouf 和Samtaney 等(2017)的研究工作都曾在浸入式边界方法的应用中采用自适应网格的方法来提升壁面处的网格分辨率,从而达到减少网格总量的目的.Wang 等(2020)在有限差分的框架下将自适应网格技术与IB 方法结合并将其应用于运动边界问题的模拟,结果表明该数值工具能够准确对包含运动边界的流动问题进行预测,且计算量相较于传统的正交笛卡尔网格大幅降低.而对于目前已经发表的湍流模拟相关工作,如Capizzano (2011,2016)、Tamaki 等(2017)、Pu 和Zhou (2018)、Berger 和Aftosmis (2018)、Xu 和Liu (2021)、Cai 等(2021)、Constant 等(2021)、Wang 等(2023)的研究工作,均采用了这种形式的网格来减少流动模拟所需的网格总量.

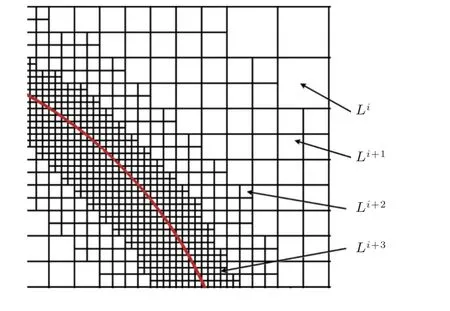
图12 采用自适应网格加密生成的多层网格系统(Wang et al.2020)

另一方面,即使对笛卡尔网格进行局部加密,想要完全满足 RANS 模型的y+要求依然需要较大的网格量,因此,上述基于笛卡尔网格的湍流模拟研究工作均采用了不同形式的湍流壁面函数来放宽对于网格y+的要求.壁面函数将近壁面的流动分为两层,外层与靠近边界的内层分别用RANS 方程和薄边界层方程来描述,对于平板问题,如果将薄边界层方程的压力项忽略则可以得到速度剖面的解析表达式,也称为显式壁面律,如方程(6)所示(Spalding 1961).Capizzano(2011)在浸入式边界方法的基础上引入显式壁面律来对湍流边界层进行建模,在此基础上对二维及三维翼型绕流进行了测试,所得到的结果与实验结果较为接近.值得注意的是,显式壁面律由于忽略了边界层内部的压力梯度,在实际应用可能导致固壁表面压力分布等参数存在一定的数值的振荡,同时对于摩擦系数的预测也会在某些压力梯度剧烈变化的区域偏离真实结果.Wang 等(2023)在锐利界面IB 方法的基础上,采用方程(6)中的显式壁面律对流动进行模拟,结果表明即使采用最为简单的显式壁面律也能够准确预测高雷诺数流动中翼型表面的压力系数分布,但是摩擦系数在局部区域的收敛性并不完美,并且同样存在一定的数值振荡.Chen 等(2023)将一种基于SA 湍流模型壁面渐进解的显式壁面模型与IB 方法相结合,计算所得到的湍流边界层速度与实验测量所得到的壁面律吻合得较好,如图13 所示.Tamaki 等(2017)、Cai 等(2021)、Chen 等(2021,2023)均尝试通过在近壁面采用经过线化后的速度梯度分布并且在壁面处施加滑移边界条件的方式来抑制数值振荡,数值结果表明虽然采用线化的速度梯度分布能够有效地抑制数值振荡,但是局部收敛性仍存在一定的偏离.

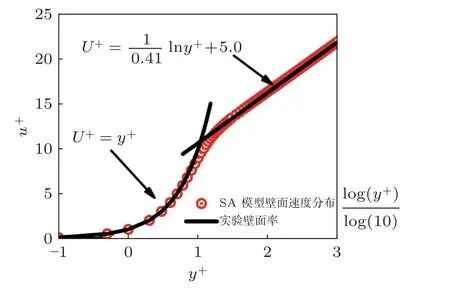
图13 基于SA 显式壁面模型的湍流边界层速度分布与壁面律对比(Chen et al.2023)

从上述研究结果来看,如何进一步提高壁面模型的准确性是目前IB 方法所面临的核心问题之一.显式壁面律的推导过程中忽略了压力梯度的影响,这一假设对于平板流动是适用的,但是对于某些存在明显压力梯度的复杂流动,显式壁面律可能存在较大的误差.为了提升对近壁面流动的刻画精度,Capizzano (2016)采用了一组包含动量、内能以及湍流输运量的边界层流动控制方程,动量方程中包含了压力梯度的影响,在每个时间步对其进行同步离散求解从而给定边界处网格单元数值,测试结果表明在某些压力变化剧烈的区域,包含压力梯度的处理方式能够使结果更接近贴体网格结果.基于边界层方程的壁面函数还被Shi 等(2019)、Ma 等(2019,2021)用于发展LES 算法以实现IB 方法在高雷诺数流动问题中的应用,上述学者的LES 模拟结果表明,实现准确预测需在边界层附近对LES 亚格子应力模型做适当的修正以平衡壁面模型所提供的摩擦应力.Berger 和Aftosmis (2018)采用了一组包含压力梯度的常微分方程对边界层流动进行描述,结果相较于显式的壁面律也表现出一定程度的改善.当压力梯度的影响被包含于边界层方程中时,无法推导得到解析的速度分布,因此需要对边界层控制方程进行同步的离散求解,这一求解过程需要耗费一定的计算时间,虽然模型的准确性及适用性有所提升,但是整体计算效率也会出现下降.Constant 等(2021)、Xu 和Liu (2021)则通过增加边界单元数量的方式在边界单元的最外层实现几乎一致的y+分布,对比结果表明采用此种处理方式,即使对于方程(6)所给出的显式壁面律,依然能够获得准确且光滑的压力及摩擦系数分布,并且压力系数的收敛性同样出现明显的改善.如何进一步提高IB 方法与壁面模型结合时的准确性以及稳定性,同时兼顾计算效率,目前仍有待深入研究.

4.2 高雷诺数内流问题的应用

目前IB 方法主要用于各类外流问题,对于这种情形,通常可以采用远大于固体边界的方形计算域并在其中布置正交的笛卡尔网格.而对于内流问题,流动通常被限制于流道内部,与此同时流道内部还可能存在运动边界,如对于上文所提到的航空叶轮机械领域的转静干涉、叶片颤振等问题,均属于这一类型.在内流条件下,流道边界所覆盖的空间范围可能远大于内部物体,如图14(a) 所示,流道边界通常是静止的,只有流道内部的固体边界可能是运动边界.从图14(b)可以看出,此时仍然采用笛卡尔网格对流道以及内部固壁边界进行建模时,用于识别流道边界所需的网格量会远超内部固壁边界所需的网格量,即使是在图14(b)中已经采用自适应网格的情形下,流道边界所引入的网格量仍然不可忽视,而在三维高雷诺数的情形下,这一问题会变得更加突出.对于图14 中所示的内流问题二维边界模型,Wang 等(2023)给出了定量的网格单元数量分析,其中用于识别整个流道边界的网格单元数量占总数量的70%左右,这一比例与流道边界覆盖的范围密切相关,当流道边界覆盖的区域越宽广,这一比例也会越高.前文中提到,IB 方法的主要优势在于处理复杂边界和运动边界问题,而图14(a)中的流道边界并不属于上述任意一种情形,因此想要进一步提高IB 方法在处理三维高雷诺数内流问题上的计算效率,则需要对流道边界的处理进行改进.

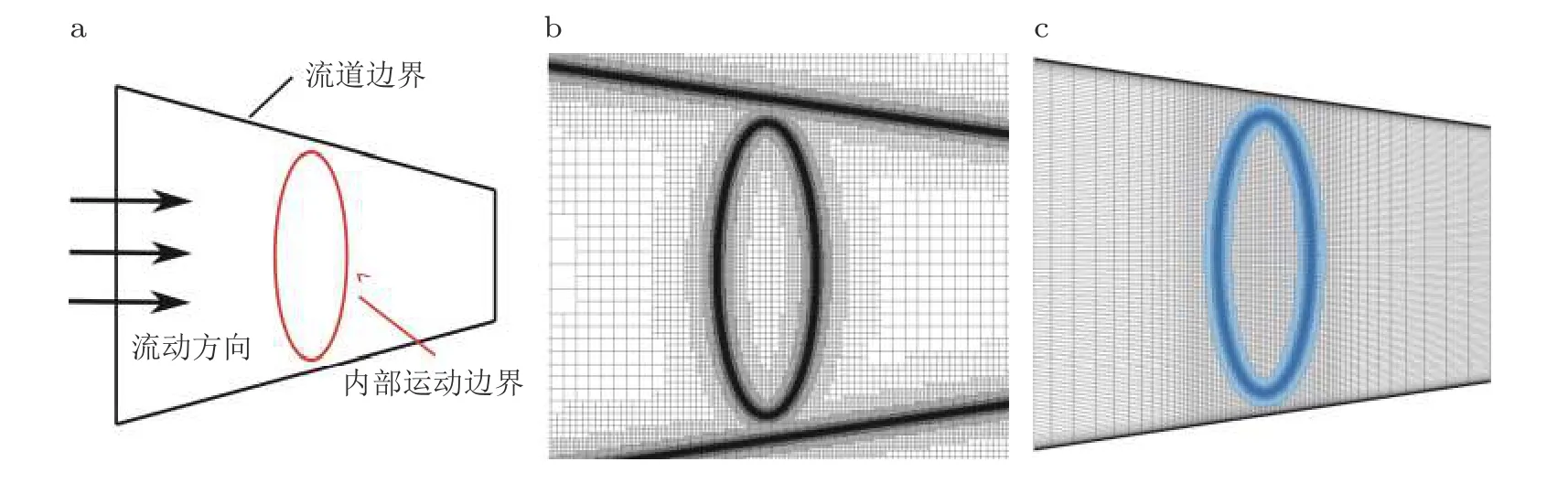
图14 (a) 内流问题示意图,(b) 采用笛卡尔网格结合自适应加密所生成的网格系统,(c) 流道贴体网格结合自适应加密生成的网格系统(Wang et al.2023)

针对内流中的运动边界问题,Ge 和Sotiropoulos (2007)提出了一种适用于曲线网格的浸入式边界方法,该研究工作首先采用曲线的贴体网格覆盖整个流道边界,然后在内部运动边界附近构造局部正交或近似正交的笛卡尔网格从而使得IB 方法能够得以应用,如图14(c)所示,该方法避免了采用笛卡尔网格对流道边界进行处理,从而达到了降低网格量、提高计算效率的目的.Ubald 等(2021)采用同样的思想对一个前缘带有圆柱扰流器的涡轮叶片进行了模拟,该研究中流道以及叶片均采用贴体网格进行覆盖,通过在叶片前缘构建局部的笛卡尔网格来应用IB 方法对圆柱扰流器进行建模从而大幅降低网格复杂程度.类似地,Mochel 等(2014)、Weiss 和Deck(2018)对火箭和导弹的主体采用贴体网格,在此基础上对部分固体型面如锯齿尾缘、推进器上的复杂结构采用IB 方法进行建模,结果表明此种手段既能降低网格的生成难度,又能够兼顾计算效率.上述工作为处理内流环境中的运动/复杂边界问题提供了一条可行的思路,但是对于更加复杂的运动边界问题还需要对上述方法进行进一步的改进以增强其处理工程领域复杂运动边界问题的能力.例如对Du 等(2016a,2016b)、Chen 等(2021)的研究工作中所关注的叶轮机械领域的转静干涉问题,此时运动边界靠近流道边界,难以在流道附近构建局部的笛卡尔网格,因此上述的方法在处理此类问题时还需要进一步改进.

Wang 等(2023)的分析表明,当流道内的运动边界靠近流道边界时,由于识别流道边界所采用的贴体网格仅沿壁面法向具有较高的分辨率,因此网格的展弦比较大,此时由于运动边界与网格单元的相对朝向未知.传统的锐利界面IB 方法是面向均匀正交的笛卡尔网格发展而来,通常采用统一的外伸插值距离,而此时由于网格展弦比较大,统一的外伸插值距离会出现失效的情形.为解决这一问题,Wang 等(2023)针对锐利界面IB 方法提出了一种自适应外伸插值距离的方法,成功将IB 方法拓展至一般的曲线网格,使其能够处理边界与不同展弦比切割的情形,结合上文提到的自适应网格加密以及壁面函数,成功对三维亚声速平面叶栅以及NASA 转子37 内部的跨音流动进行了模拟.结果表明,该方法能够获得与贴体网格一致的结果,并且能够准确预测叶栅叶片表面的压力分布以及跨音转子的特性曲线,其中叶栅叶片表面的压力分布数值模拟结果及其与实验的对比如图15 所示.在此基础上,Chen 等(2023)采用上述方法对一低压涡轮叶栅以及涵道风扇流动进行了数值模拟研究,结果表明该方法同样能够准确预测不同工况下叶片表面压力及下游尾迹的分布状况,而计算效率相较于采用传统的正交笛卡尔网格而言大幅提高.上述研究表明,采用自适应外伸插值距离能够提高IB 方法与不同类型网格的结合能力从而拓宽方法的适用范围,但值得注意的是,Tamaki 等(2017)、Berger 和Aftosmis (2018)、Chen 等(2023)、Wang 等(2023)的研究均表明,对于实际工程领域的高雷诺数流动,流场中可能存在流动分离现象,采用湍流壁面模型在这些分离区域可能出现明显的预测偏差,但是目前IB 方法在高雷诺数流动的应用中仍然非常依赖于壁面模型来提高计算效率.因此,如何进一步提高该方法对不同类型复杂流动的适应能力是将其推向工程应用所需要解决的关键问题之一,一种可能地解决手段是采用脱体涡方法或大涡模拟等高保真模拟方法来提高复杂流动的预测精度,但其对计算资源的需求使其目前还无法实现规模化工程应用.

图15 三维亚声速平面叶栅叶片表面压力分布数值模拟结果及其与实验的对比(Wang et al.2023)

5 总结

本文主要对IB 方法中边界的建模方式,在复杂边界、运动边界以及运动边界发声问题等问题的应用以及高雷诺数流动模拟中的研究进展进行了综述.目前IB 方法已广泛应用于诸如生物体流动等各类的低雷诺数流动研究中,其核心优势在于处理复杂边界以及运动边界的情形.而对于航空航天、建筑桥梁等领域中包含多运动边界的复杂工程问题,IB 方法也有所涉及且同样能够有效地降低网格复杂程度,但由于这些流动通常具有较高的雷诺数,而实现高雷诺数流动的准确模拟需要投入大量的计算资源,目前实现大规模的应用仍需要进一步的研究.未来研究的关键在于进一步提高IB 方法针对高雷诺数流动的计算效率,同时提升计算模型处理三维复杂高雷诺数流动现象的能力.

致 谢国家自然科学基金(52022009)资助项目.