显微拉曼光谱力学实验方法与应用研究进展

仇 巍 常 颖 亢一澜 谢海妹,*

1 天津大学机械工程学院力学系,天津 300350

2 天津市现代工程力学重点实验室,天津 300350

1 引言

当今纳米材料、软物质、多尺度与多场耦合等力学前沿科研方向,对发展多种不同功能的实验力学技术提出了迫切的研究需求.与此同时,在国家重大需求中,如航空发动机与燃气轮机中的热障涂层、半导体微电子集成器件、柔性电子器件、能源材料与器件,其核心部件可靠性的设计与应用,对实验力学也提出了重要的极具挑战性的测量难题.因此,深入开展实验力学测试技术研究,并吸收相关领域科学进展,丰富力学测量技术体系,发展不同类型、多种功能、更加精细的实验力学测试技术具有重要的科学意义与明确的应用需求.

近年来,在上述科学背景与科研需求的推动下,作为光谱实验技术之一的拉曼光谱力学测量与分析发展迅速.该方法的特点包括高空间分辨力 (可达200 nm)、高测量时效 (单点时间分辨力为秒级)、无损非接触、样品无需制备、对本征应力和非本征应力均敏感等 (Qiu &Kang 2014,雷振坤等 2015).相比大多数适于形貌和位移场分析的光测类实验力学方法和电子显微技术,显微拉曼光谱可实现应变的直接测量,无需通过变形来反演应变和应力.同时,显微拉曼实验装置易于与力学及其他加载装置联用,适合于原位、在线甚至活体的力学表征.此外,拉曼光谱技术对材料一定深度处的力学性能具有探测能力,能够实现材料浅表层的力学行为分析.

采用拉曼光谱开展力学领域的实验分析,其历史源于20 世纪中叶物理学与材料学领域的研究者发现了拉曼光谱对晶体材料的应力/应变等力学参量敏感的特性 (Loudon 1964,Ganesan et al.1970,Anastassakis et al.1970).de Wolf (1999)于20 世纪末给出了简化的应力-频移关系,使得拉曼力学测量得以推广,Young 等提出了基于实验标定的拉曼力学分析方法 (So &Young 2001,Eichhorn &Young 2004),Zhao 等提出了拉曼力学传感技术 (Zhao et al.2001,Zhao &Wagner 2003).天津大学Kang 等 (2005)在国内较早开展了拉曼光谱实验力学的方法与应用研究.经过数年的发展,以显微拉曼光谱为代表的光谱实验方法已成为微尺度实验固体力学测量与表征的重要手段.

本文首先从物理力学框架、简化近似模型、精细表征理论以及拉曼应变传感等方面,论述了显微拉曼力学表征的实验力学原理.随后,针对偏振测量、全谱形分析、角度分辨拉曼以及拟合识别等,着重介绍了拉曼光谱用于力学研究的若干关键技术.在此基础上,本文围绕低维材料的内应力、微结构的工艺与服役应力以及微尺度界面力学实验研究三个方面,综述了基于显微拉曼实验的力学前沿研究进展.最后讨论了显微拉曼光谱在实验固体力学领域的发展前景与方向.

2 拉曼力学表征实验理论

2.1 光谱力学理论框架

拉曼光谱力学分析基于如图1 所示的理论框架: 通过材料的本构关系给出了应力-应变的定量描述,假定其在弹性变形时符合广义胡克定律;材料的晶格动力学特征方程给出了光学声子与晶格应变的线性关系;基于材料点群的拉曼张量以及入射与散射光矢量,决定了实测拉曼光谱的特征峰频移信息与光学声子的振动模式,即拉曼选择定则.以此为基础建立应力与拉曼特征峰频移变化的关系,并通过检测拉曼频移变化来实现应变/应力的定量分析.

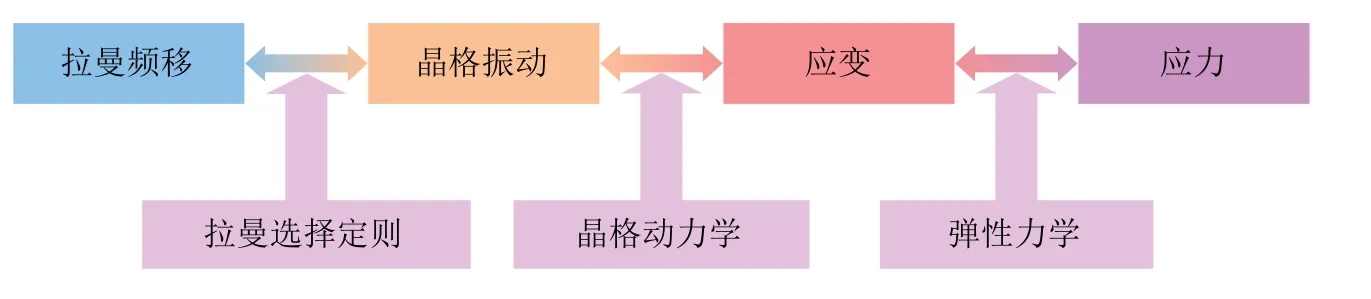
图1 拉曼光谱力学分析的基本理论框架 (Qiu et al.2018)

该理论框架中,晶格动力学的特征方程 (Secular equation) 如式 (1)

其中,εuv为应变分量;Kuvij为声子变形势张量分量,且Kuvij=Kijuv=Kvuij=Kuvji,i,j=1,2,3.设晶格无应变与有应变状态下样品的拉曼频移分别为ω0和ωk,频移增量为Δωk,则式 (1) 特征根λk=ωk2-ω02=2ω0Δωk.拉曼选择定则如式 (2)

其中,C是常数;eI与eS分别为入射光和散射光的偏振矢量;Rl为声子l(l=1,2,3) 的拉曼张量(Qiu et al.2018).

该理论框架的构建经历了以下发展过程.Loudon (1964) 给出了32 个对称点群各自的拉曼张量,为针对晶体材料的定量拉曼分析奠定了基础.Ganesan 等 (1970)针对金刚石类的晶体结构,建立了考虑应变对光散射特征影响的晶格动力学方程.Anastassakis 等将晶格动力学与弹性力学相结合,推导了硅、锗等典型半导体材料拉曼力学分析的理论模型,并先后测量、修正了硅材料的声子变形势常数 (Anastassakis et al.1970,Anastassakis et al.1990,Cai et al.1993,Anastassakis.1997,Kaltsas et al.1998).然而,事实上Anastassakis 等早期建立的拉曼光谱信息与材料应力的基本关系尚比较复杂,因诸多材料参数 (如参量r/a/γ/θ/α/β) 未知且物理意义不明确,这使得拉曼光谱很难实用于力学分析,如式 (3) 所示 (Anastassakis et al.1990)

2.2 简化近似模型

基于前期的理论模型,de Wolf 等 (1999)提出忽略切应力影响的简化模型,给出了 (100)晶面单晶硅单向/等双轴应力下的拉曼频移-应力关系式

其中,σ实际上等于被测表面面内的主应力和.采用标定实验,de Wolf 等 (1996)验证了简化模型在单向应力状态下的正确性,如图2(a).这一基于应力状态简化和实验标定的成果,为拉曼光谱力学分析方法得以在半导体产业广泛应用奠定了基础.在该简化模型基础上,不同团队针对各种金刚石类晶格的材料及其各自所研究的问题对模型进行了改进和修正.例如,Li et al.(2010) 从模量变化的角度对多孔硅材料的拉曼频移系数进行了修正;Dychalska 等 (2015) 通过研究金刚石1332 cm-1处的拉曼峰,研究了Si (100) 衬底上沉积的CVD 金刚石薄膜在30 ℃至480 ℃温度范围内的应力温度依赖性,给出了金刚石表面的残余应力分布;Myers 等 (2014)得出多晶硅在单轴拉伸下的应力频移因子为-522.5 MPa/cm-1,以此为基础研究了微加工多晶硅器件在不同单轴拉伸水平下的应力分布;Gassenq 等 (2016)使用微桥装置并结合同步辐射XRD 给出了锗的拉曼-应变关系,如图2(b) ;Tsang 等 (1994)提出了修正声子限制效应对拉曼频移影响的经验关系,Qiu 等 (2016)在此基础上提出了硅锗固熔合金应力表征的混合模型.

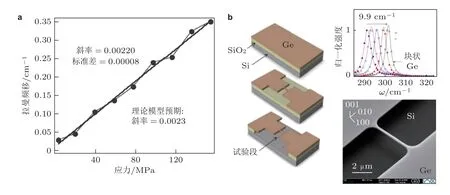
图2 单向应力下背散射拉曼频移-应力关系标定实验.(a)(100)单晶硅 (de Wolf et al.1996),(b) 单晶锗 (Gassenq et al.2016)

采用图1 所示的物理力学理论框架与工程简化方法,能够建立大多数具有规则晶格结构的非金属晶体材料的拉曼频移-应力关系,尤其是高级晶族和中级晶族.上文论述的单晶硅属于立方晶系,为高级晶族.中级晶族的代表有四方晶系TiO2(Alhomoudi &Newaz 2009)、BaTiO3(Pezzotti et al.2012),三方晶系Al2O3(Pezzotti &Zhu 2015),六方晶系4H-SiC (Sakakima et al.2018)、6H-SiC (张银霞等 2019)、CdS (Briggs &Ramdas 1976)等.有关四方晶系材料的研究中,Pezzotti 等 (2012)针对BaTiO3晶体采用线性变形势理论,假设扰动势与线性应变项成正比,以此简化给出由扰动势表达的声子变形势系数,并进一步求解晶格动力学方程,得出E 模的频移-应力关系.对于六方晶系4H-SiC,Sakakima 等 (2018)基于Briggs &Ramdas 的分析,建立了4HSiC 的拉曼频移与应力之间的关系,如式 (5)

对于这些工作给出的结果,如式 (5) 所示的应力频移关系,在尚未知应力状态的情况下,很难通过拉曼测量定量给出应力状态及其分量的真实情况.此时,采用类似de Wolf 简化应力状态的手段则更适用于工程分析.Kim 等 (2020)给出了忽略晶向、简化应力状态并结合标定的4HSiC 的应力频移关系,如式 (6)

此外,Wang 等 (2014)针对单晶6H-SiC 也采用了相同的分析手段.类似工作还有,Olego 和Cardona (1982)研究了3C-SiC 静水压条件下应力与拉曼频移的关系;Demangeot 等 (1996)建立了氮化镓类材料的频移-应力/应变关系;Shafiq 和 Subhash (2014)利用三维碳化硅晶体和锌-闪锌矿晶体的声子变形势,建立了碳化硅颗粒的拉曼峰频移与约束应力大小之间的关系.

以上及类似的工作,均是通过简化材料的应力状态,给出了单轴、等双轴或者等效应力与频移的定量关系,再结合标定实验验证所给出的定量关系的正确性.然而,这种对应力状态的简化,事实上是将应力作为标量处理,测量得出的结果实际上是一个等效的应力 (通常是主应力和),只适用于其标定的应力状态,不仅无法体现应力张量各分量的具体情况,而且在非标定方向上的分析误差较大.总之,这是一种半定量或者有限定量的实验分析.特别是,经典的简化模型通常忽略切应力的影响.而实际上切应力对于实测的拉曼频移存在不同程度的影响,这在Li 等(2015)、Ahmed 等 (2011)、Stievater 等(2005)各自的工作中得到了实验验证.Ma 等 (2021a)基于偏振拉曼,对切应力的影响进行了定量分析,发现实际上只有 (001) 晶面上的拉曼信号对切应力“脱敏”,而其他晶向则不能忽略.

2.3 量化分量模型

Qiu 等 (2018)以硅基材料为范例,给出了定量表征随机晶面复杂应力状态下各应力分量的量化分量模型.首先,如图3,依据单晶硅晶体结构建立“晶体坐标系”和“样品坐标系”,利用坐标变换将晶体坐标系下的应力σ、应变ε、材料柔顺系数常数张量S、声子变形势张量K(均用Voigt 记号模式表达) 等转换到样品坐标系下 (在右上角加“′”标志样品坐标系下的参量),从而得到式 (7)

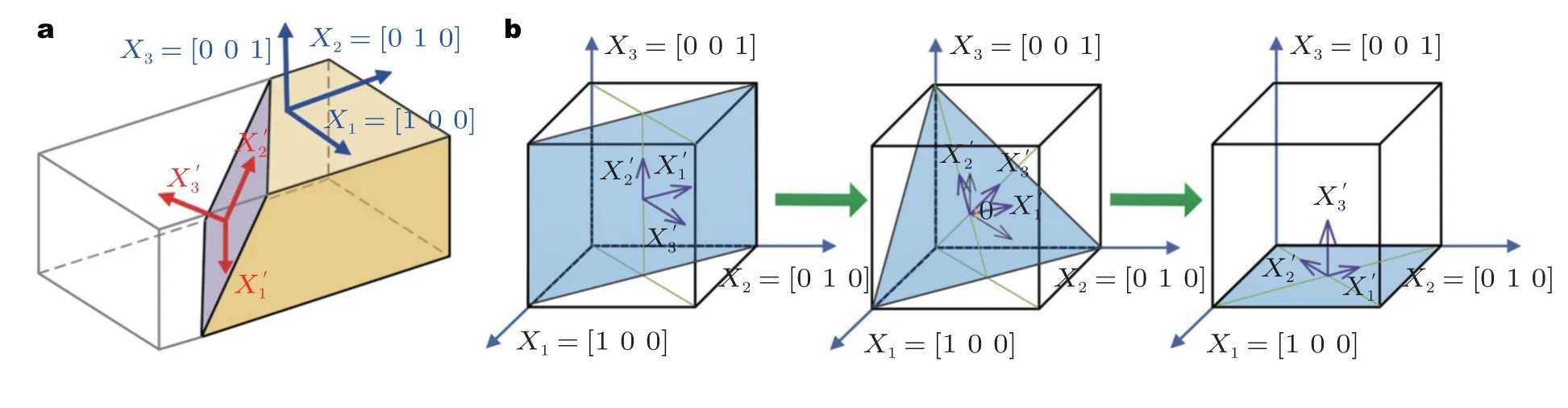
图3 (a) 晶体坐标系和样品坐标系示意图,(b) 随机晶面旋转过程示意图 (Qiu et al.2018)

其中,Hε和Hσ均为坐标变换矩阵.同理,获得样品坐标系下的拉曼张量Ri′及各自对应方向矢量V′i.考虑到样品坐标系下晶格动力学特征方程的特征根λ′k所对应的特征向量n′k与拉曼张量Ri′对应的方向矢量V′i通常不一致,因此样品坐标系下的拉曼选择需要使用其方向矢量与特征向量n′k一致的拉曼张量R"k

此时,若在单个特征峰中可以看到两个以上的拉曼模,可根据以下关系式获得实测波数增量的表达式 (Young &Day 2010)

基于式 (2)、(7)～ (9),当被测对象的应力状态已知时,能够采用如下通用的拉曼力学关系

其中,σ为待测应力;Δωobs为实测的频移;κ为研究对象所在晶向与应力状态下对应的应力-频移因子.Qiu 等 (2018)给出了单晶硅常用晶面在典型应力状态下的应力-频移因子.

由表1 可见,即便在简单的应力状态下,不同晶向不同应力状态的应力-频移因子仍存在明显的差异 (通常也因入、散射光的偏振矢量不同而不同).而对于未知复杂的应力状态,则需要结合偏振技术构建联立方程组,才可能实现应力状态各分量的解耦分析,本文将在后文偏振拉曼技术部分给出讨论.需要注意的是,在已发表的绝大多数拉曼应力分析工作中,普遍采用了 (100)晶面单轴应力下的应力-频移因子,忽略或无视所研究对象的晶面与应力状态,从而导致其分析结果时常与事实不符.量化分量模型则针对具体的被测晶面给出了应力分量与拉曼频移之间的量化关系,能够正确表征随机晶面上复杂应力状态的分量信息.

表1 单晶硅常用晶面在简单应力状态下的应力-频移因子 (Qiu et al.2018)

2.4 基于标定的测量与传感方法

基于频移系数标定为基础的实验测量也是拉曼力学分析的重要手段.相比前述基于频移-应力理论模型的拉曼力学分析,基于标定的方法更适用于没有规律性的晶格结构但含有拉曼活性化学键的材料 (例如大多数高分子材料).特别是对于可以确定应力状态的问题,比如纤维增强复合材料中的纤维,基于标定的测量取得了诸多有影响力的研究成果.例如,Young 等利用碳纤维、大麻纤维、聚对苯并异恶唑 (PBO) 纤维等的分子共价键,研究了各自拉曼特征峰频移对键长变化的敏感性,通过步进的单轴拉伸实验获得各材料的应力-频移因子,并以此为基础围绕纤维复合材料界面力学行为开展了一系列实验分析 (Lei &Young 2001,Young et al.2010).Lei 等则利用凯夫拉纤维在1600 cm-1附近特征峰的应力敏感性,基于拉伸标定 (如图4) 开展了纤维微滴 (Cen et al.2006)、桥联 (Lei et al.2013a)、推出压入 (Lei et al.2018) 等界面力学实验研究.

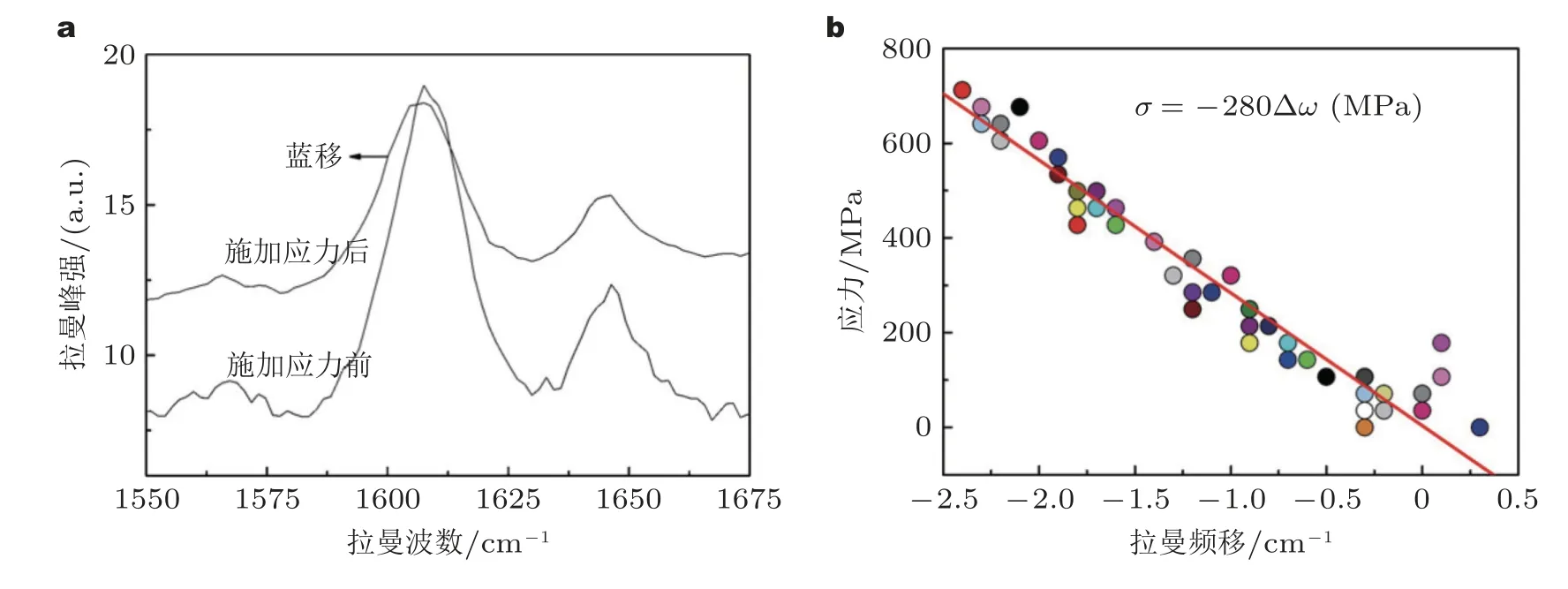
图4 (a) Kevlar -29 纤维施加应力前后拉曼G 峰峰位,(b) Kevlar -29 纤维的G 峰拉曼频移随应力的变化 (Lei et al.2010)

对于不具备拉曼活性的大多数材料则可以采用拉曼传感的手段,即以具有拉曼活性的材料作为传感介质实现非活性材料应变的测量.例如,Young 等 (2001) 将玻璃纤维表面涂覆一层含二乙炔聚氨酯的共聚物,利用其分子链中定向排列的C=C 键和C≡C 键,实现纤维界面位置指定方向应力变化规律的定量分析.Miyagawa 等 (2001a,2001b,2002) 以PBO 薄膜作为拉曼传感器,研究了多向碳纤维增强塑料 (CFRP) 的I 型和Ⅱ型断裂韧性,给出了裂纹尖端附近的应变分布.Wagner 等提出了碳纳米管应变传感,采用单壁碳纳米管作为传感介质实现了复合材料中基体内部的应变分析 (Zhao et al.2001,Wood et al.2001).Ruan 等 (2003,2006)则利用多壁碳纳米管的拉曼活性分析了尼龙纤维大变形过程中的高分子-纳米管杂交复合材料内部结构演化,并基于实验结果提出了碳纳米管改善聚乙烯力学性能的理论模型.Qiu 等 (2010)在Wagner 工作的基础上,提出了碳纳米管传感面内应变分量的理论模型并发展了拉曼应变花技术,本文将在拉曼关键技术中讨论该工作.黄浩等以纤维表面碳涂层为传感介质,采用显微拉曼光谱探测碳化硅纤维增强钛合金复合材料,得出碳化硅纤维受到的残余压应力约为705.0 MPa (黄浩等 2017).类似地,Feng 等 (2022)研究了等离子喷涂SiC 涂层的碳/碳复合材料中的亚层厚度与残余应力对烧蚀行为的影响机制.

3 拉曼力学测量的表征方法与关键技术

如何从显微拉曼光谱力学实验中获取具有较高置信度的测量值涉及若干技术环节,其中三个主要环节包括光谱探测、数据处理与力学量提取.本章分别简介这三个环节中的核心内容与研究进展.

3.1 基于偏振拉曼探测的应力/应变表征方法

偏振拉曼为实现应力/应变分量的定量分析提供了具有广泛应用前景的实验手段.偏振拉曼探测技术是通过对入射光和/或散射光偏振矢量的控制,形成所需的入射光与散射光偏振矢量组合 (偏振构型) 下的拉曼测量.偏振拉曼探测技术利用激光的偏振特性,并将其与被测材料的晶体学、光学或力学各向异性特征相结合,能够获取包含力学参量方向特征的光谱信息.在进行力学分析时,利用公式 (2) 给出的偏振选择关系,通过激发和收集特定偏振构型下拉曼信息的选择性,再利用晶格动力学特征方程式 (1),就可能实现应力或应变分量的定量表征.

偏振拉曼技术与装备的技术进步 (Alonso et al.2015,Mao et al.2018)推动了拉曼力学研究的进展.例如,Pezzotti 和 Zhu(2015)分别在平行和正交的偏振状态下转动样品角度来探测拉曼信号变化,得出了多晶氧化铝中的应力分量场 .采用类似手段,Rho 等 (1999,2001)基于拉曼偏振选择规则,开展了两个横向光学声子的拉曼扫描成像,给出了SiGe/Si 光波导结构中的应力分布.Wagner 等提出了以随机分布的碳纳米管为传感介质的应变传感,忽略轴向与偏振方向不平行碳纳米管的贡献 (该简化思路被证实是错误的),以平行偏振构型下的拉曼测量结果直接线性对应入射光偏振方向的应变分量 (Barber et al.2004,Frogley et al.2002).Pezzotti 和 Zhu(2015)针对刚玉 (多晶α-Al2O3) 材料,将其各振动模式的拉曼选择规则扩展为空间3 个欧拉角和4 个拉曼张量分量的显式函数,提出了基于偏振拉曼表征刚玉应力的分析方法.Nuytten 等 (2017)研究表明,使用正确的拉曼散射偏振构型,Ge、SiGe 以及InGaAs 的周期性通道半导体阵列的拉曼响应可以显著增强,这种效应可用于实现半导体纳米结构内部的成分分析和应力分析.张飒和梁丽苹 (2017) 实现掺镧锆钛酸铅 (PLZT) 压电陶瓷在不同压应力作用下试样的原位拉曼测试,发现不同压应力下拉曼软模E(2TO)和E(3TO+2LO)+B1 的峰强均随散射偏振角度呈现正弦式的变化规律.

偏振拉曼探测是实现材料表面复杂应力状态各应力/应变分量解耦分析的关键手段.具体而言,由于被测表面的三个应力分量都对拉曼光谱的频移信息产生不同程度的影响,而利用偏振拉曼则能够通过三个 (或者多个) 不同偏振角度下的拉曼测量,构建由不同偏振下拉曼频移与三个面内应力分量之间关系的联立方程组.通过将实测的拉曼频移代入方程组,就能够将应力分量对频移的影响解耦出来,实现各面内应力分量的定量分析.例如,Ma 等 (2019)给出了正交偏振构型下 (110) 晶面单晶硅的三个面内应力分量与偏振拉曼频移的联立关系式

其中,实测拉曼光谱频移增量Δω的小角标数字表示入射光的偏振角度.进一步地,马路路(2020)通过忽略高阶量的影响,给出了 (111) 晶面在两向应力状态下的主应力分量与偏振拉曼频移的联立关系式

基于偏振拉曼的测量能够实现大多数晶面上应力状态各分量的解耦分析,但也存在一些特例,例如单晶硅的 (100) 晶面.在 (100) 晶面上,垂直背散射的拉曼散射中只有LO 振动模可见,这导致晶格动力学特征方程只剩下与LO 振动模相关的部分,未知量多于独立的方程数量而难以定解,故而采用普通的偏振拉曼仪器无法实现 (100) 晶面上各应力分量的解耦分析.为此,柴俊杰等(2019)提出了倾斜背散射的拉曼探测技术与实验装置,Fu 等 (2020)则采用该技术实现了 (100) 晶面上两向应力的分量解耦分析.

类似的问题还发生在一些中级晶系的材料上,例如BaTiO3、Al2O3的E 模以及石墨烯的G模都是双重简并的.在面内的三个应力分量均未知的情况下,这些材料的拉曼-应力关系同样存在未知量多于独立的方程数导致难以定解的情况.但若应力状态或者其中某一个应力分量已知,例如已知应力状态中各主应力的相互关系或已知主应力方向,偏振拉曼将能够实现应力分量的解耦分析,而这种应力状态部分已知的情况在实际工程中也是较为常见的.所以,偏振拉曼被认为是突破力学参量“半定量”测量瓶颈,实现分量解耦分析的关键技术.

偏振拉曼还能够用于对非拉曼活性材料表面应变分量场的传感测量.一些低维材料 (例如碳纳米管) 的拉曼光谱对变形较为敏感,而且其拉曼散射的强度对拉曼探测的偏振方向具有选择性 (称为天线效应),可能成为面内应变分量定量测量的传感介质.Qiu 等 (2010)以偏振拉曼为基础,提出了基于碳纳米管为传感介质的拉曼应变传感理论模型和实验方法.相比Wagner 忽略非平行方向碳纳米管贡献并采用单向标定的方法 (Barber et al.2004,Frogley et al.2002),Qiu 等(2010)提出了模型计及随机方向上任一单个碳纳米管对整个拉曼光谱的合成贡献,并通过构建测点内所有碳纳米管对实测频移的统计学关系,得出碳纳米管传感贴片的偏振拉曼频移与平面内应变分量之间的解析关系.采用三个互不相同的偏振方向分别对同一位置进行拉曼信息采集,则能够建立联立方程组给出各应变分量的显性表达,该方法称为拉曼应变花

其中,ΔΩ表示实测的频移增量,其下角标为拉曼探测的偏振方向,Ψ为传感系数,εX、εY、γXY分别为待测的面内三个应变分量.应用拉曼应变花,Qiu 等 (2013)分别给出了单向纤维增强环氧复合材料横向直角楔口附近四点弯载荷下的应变分量场 (如图5).

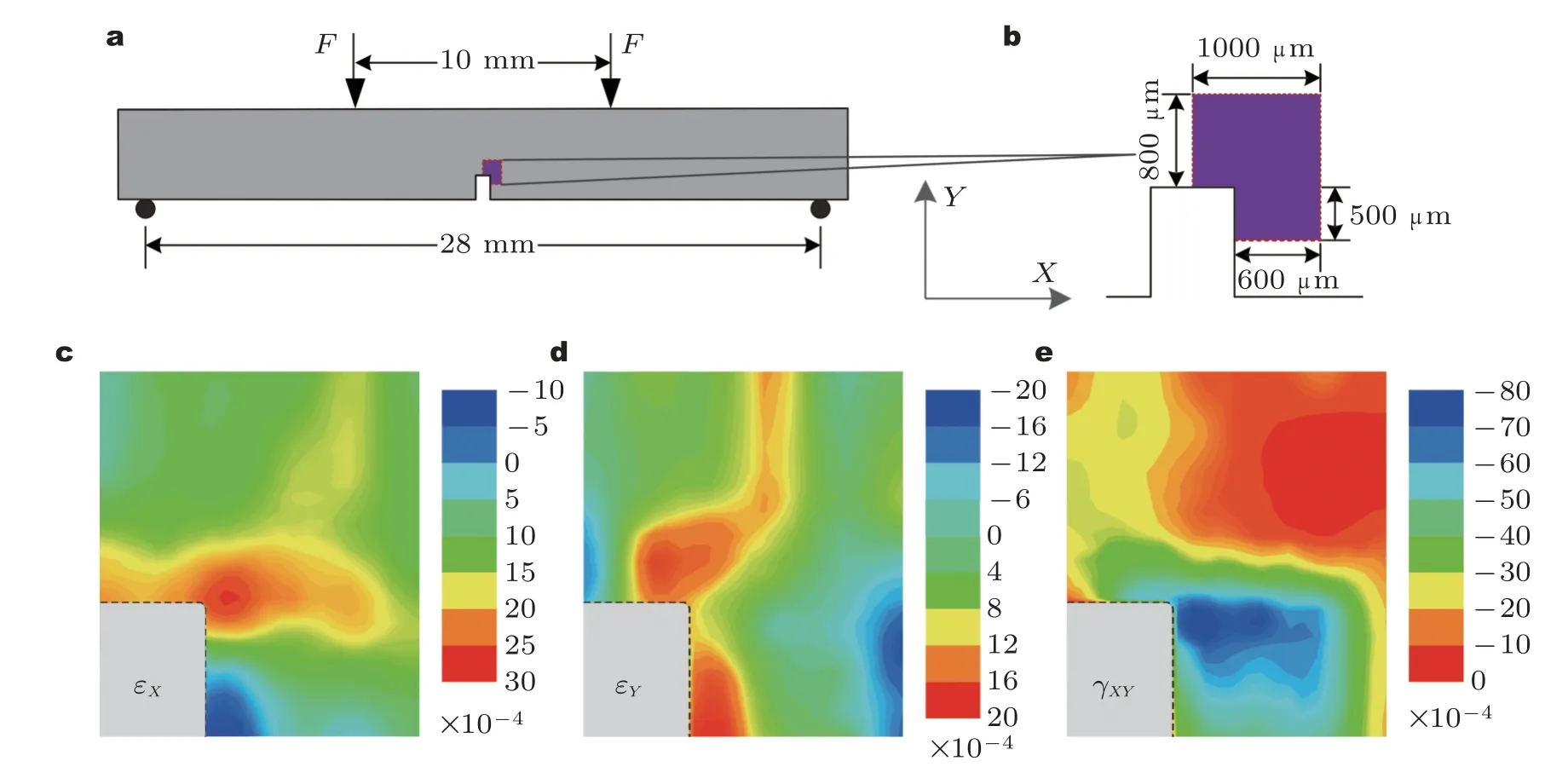
图5 纤维增强材料四点弯矩形楔口局部应变场 (Qiu et al.2013).(a) 试件与加载方式,(b) 拉曼扫描区域,(c) 实测εX 应变场,(d) 实测εY 应变场,(e) 实测γXY 应变场

综合以上,无论是晶体材料应力分量的定量解耦还是基于碳纳米管的面内应变分量传感,采用偏振拉曼技术,实现了将光谱力学分析从传统的半定量/有限定量的等效应力/应变分析,提升到了应力/应变面内各分量的定量分析.

3.2 基于光谱曲线拟合的数据处理技术

与大多数光测力学实验方法的实测数据是光学图像不同,显微拉曼实验给出的测试结果是由若干离散数据点强度值构成的光谱谱线.拉曼光谱谱线包含若干个晶格振动模所对应的特征峰,各特征峰的主要参数有峰位ω、展宽 (半高宽,FWHM) 和峰强p等.通过对谱线的数据处理得出峰位信息ω的相对变化是开展拉曼力学分析的必要环节.峰位提取的精度和可靠性,在分析层面上 (正确地表征模型是理论层面) 决定了应力分析是否准确.

对于由离散数据点构成的拉曼光谱数据,一些物化分析研究中通常是以强度最大的采样点的波数作为峰位,这类处理方式的分辨率远低于应力/应变所需的精度而不适于力学表征.对离散数据进行特征峰曲线拟合是应力分析通用的做法,其关键是拟合函数的选择.一般而言,实测的拉曼特征峰形状往往是Lorentzian 函数和Gaussian 函数卷积的曲线,即Voigt 函数曲线.在实际应用中,大多数研究者采用其简化形式Psd-Voigt 函数来拟合拉曼光谱数据.但究竟哪种函数曲线更适合于力学分析,即能够准确地量化应力/应变对频移的影响,长久以来尚缺少相关工作.近期,一些针对荧光光谱的工作结果可以作为借鉴.Lu 等 (2021)与Zhang 等 (2021)分别对红宝石荧光光谱和稀土荧光光谱的力学分析拟合方法进行了物理实验与数值实验相结合的研究,发现Psd-Voigt 函数虽然能够获得最佳的拟合优度 (goodness of fit,GOF),但其代价是在毫无物理意义的情况下调控Psd-Voigt 函数中Lorentzian 部分和Gaussian 部分的占比,导致数据分析对应力不敏感,难以识别微小应力引起的峰位变化,因此并不适用于力学研究.

近年来,针对越发复杂的研究对象和力学问题,发展出了诸如分峰、全谱形分析等新的拉曼光谱数据分析手段.例如,当分析对象的拉曼特征峰出现简并 (峰位重合或者比较接近) 的情况时,分峰是一个重要的选择.Dou 等 (2018)在双层多晶石墨烯界面力学行为研究中,提出了石墨烯2D 峰分峰方法,并用于提取上、下层石墨烯的应变信息,如图6(a).Mohiuddin 等 (2009)发现,单向拉伸载荷下石墨烯双重简并模E2g分裂成两个,这导致石墨烯的G 峰在应变较大时分裂成两个亚峰G+和G-.Naumis 等 (2017)从理论层面分析了应变对石墨烯及其他二维材料的电子和光学性质的影响,指出导致G 峰的LO 和TO 模分裂的原因在于单轴应变打破了石墨烯的对称性,产生分峰现象.Liu 等 (2021)采用化学手段制备了上下层分别采用不同同位素 (13C 和12C)的双层石墨烯,利用两种同位素同一振动模形成的自然分峰来消除简并,实现了不同堆叠模式石墨烯上下层界面行为的实验表征.

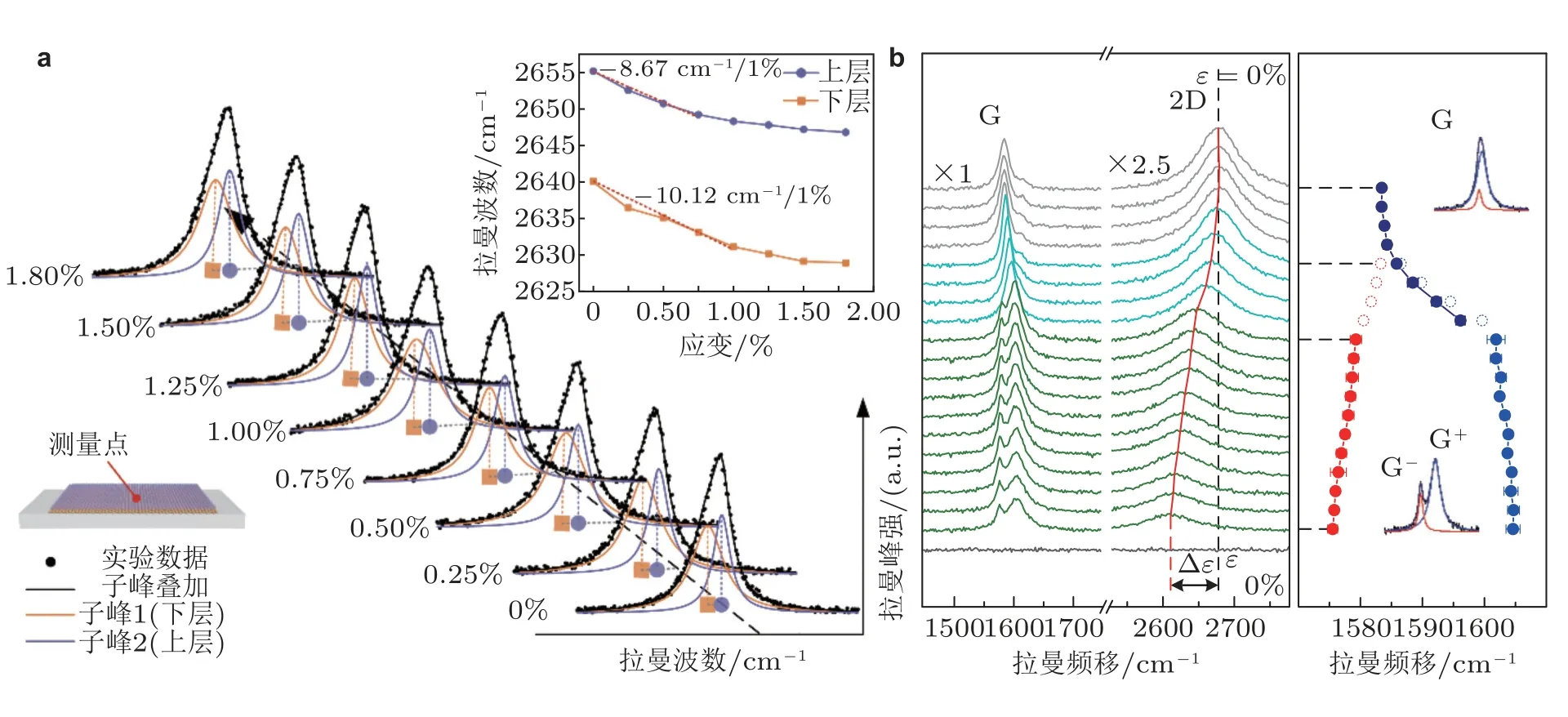
图6 (a) 双层石墨烯2D 拉曼峰的分峰分析 (Dou et al.2018),(b) 全谱形分析用于研究石墨烯电极电化学诱导力学行为 (Song et al.2022).

在分析多尺度/多级结构的力学研究时，综合利用频移、展宽、峰强以及不同特征峰的峰强比等“全谱形”信息更能够发挥关键作用.例如,Li 等 (2012)围绕纳米管纤维的实验发现,单纯的频移分析已难以满足多尺度界面行为的研究需求,为此提出了综合利用强度、展宽、峰位变化的全谱形分析方法,实现了多级结构界面行为及其对材料宏观强韧性影响的定量分析.Deng等 (2014)在研究碳纳米管纤维破坏机理时,利用2D 峰表征平均应变,通过分析D 峰强度未发生变化来判断在纳米尺度的双壁纳米管本身没有发生损伤断裂.Song 等 (2022)在研究石墨烯电极电化学诱导力学行为过程中,如图6(b),利用D 峰与G 峰的强度比量化石墨烯的缺陷尺寸,利用G 峰分峰后两个子峰的强度比表征石墨烯结构嵌锂阶数,利用G 峰两个子峰的频移来解耦膨胀应变与电子注入的影响,利用2D 峰频移检测石墨烯应变,通过对同一谱线多个峰的全谱形分析实现了基于显微拉曼的微尺度力-电化学行为高通量表征.同样,Xu 等(2019)综合利用强度、展宽、峰位变化表征了石墨烯2D 峰的应变,发现当石墨烯受到拉伸或压缩应变时,2D 峰值强度降低,频移发生相应的左移或右移,半高宽略有增加,由此发现石墨烯界面结合能的“率相关性”新现象.

3.3 基于角度分辨拉曼的参量精准提取技术

从实测的拉曼数据中提取出所需表征的力学参量是拉曼光谱力学表征的关键环节.将曲线拟合得出的频移信息直接带入拉曼力学表征模型是最直接的手段,但这对拉曼探测数据置信度的要求较高.然而,单个测点频移置信度低是显微拉曼技术的固有问题,这成为制约光谱力学定量分析的“短板”.当前,研究级显微拉曼光谱仪的光谱重复性 (系统随机误差) 均为0.1 cm-1左右,这意味着近50 MPa 量级的应力表征随机误差 (Spengen et al.2000).特别是当开展应力/应变分量的解耦分析时,系统的随机误差以及偏振角度控制的初始与随机误差等呈现误差传递、繁殖现象,应力分量表征的结果时常与真实情况有较大差距.而已有工作中研究者普遍采用的大批量重复实验取平均值的手段,实际上难以有效控制误差影响 (Qiu et al.2022).

角度分辨拉曼是开展基于光谱的力学精细、精准表征的主要发展方向之一,其关键优势是能够有效提升光谱力学分析的置信度.“角度分辨”光谱测量的概念最早源自于X 射线衍射技术(XRD),是通过连续控制某个或某几个激发或测量的角度参量,在一定范围内以确定的空间分辨率扫描获得不同角度参量组合对应的光谱/光强信息,构成角度参量-光谱信息序列.角度分辨拉曼,是指探测 (激发与收集) 倾角、样品转角与入/散射光偏振角等角度状态参量部分或全部可调可控的显微拉曼探测及其相关的数据分析技术.近年来,角度分辨成为了拉曼技术发展主流趋势之一.

与普通显微拉曼或偏振显微拉曼相比,角度分辨拉曼测量能够建立光谱信息与各可调可控的角度状态参量之间唯一的、确定的对应关系,能够实现普通偏振拉曼所不容易,甚至无法实现的光谱定量分析.例如,Ma 等 (2021b)采用角度分辨拉曼光谱测量步进控制的偏振角对应的光谱信息,并以拉曼应力表征模型为基础,利用拟合迭代算法从角度分辨拉曼信息中识别出 (1 1 0) 硅的各应力分量,其得出的三个应力分量平均相对误差均 ＜ 5%,如图7.可见,基于角度分辨拉曼测量并配合拟合迭代识别的力学信息提取技术 (相比基于三个角度偏振拉曼测量联立求解应力分量的解析法) 能够大幅提升应力表征的置信度.总之,围绕角度分辨拉曼,发展抑制误差的信息提取技术是提高拉曼力学分析置信度的一类重要手段.

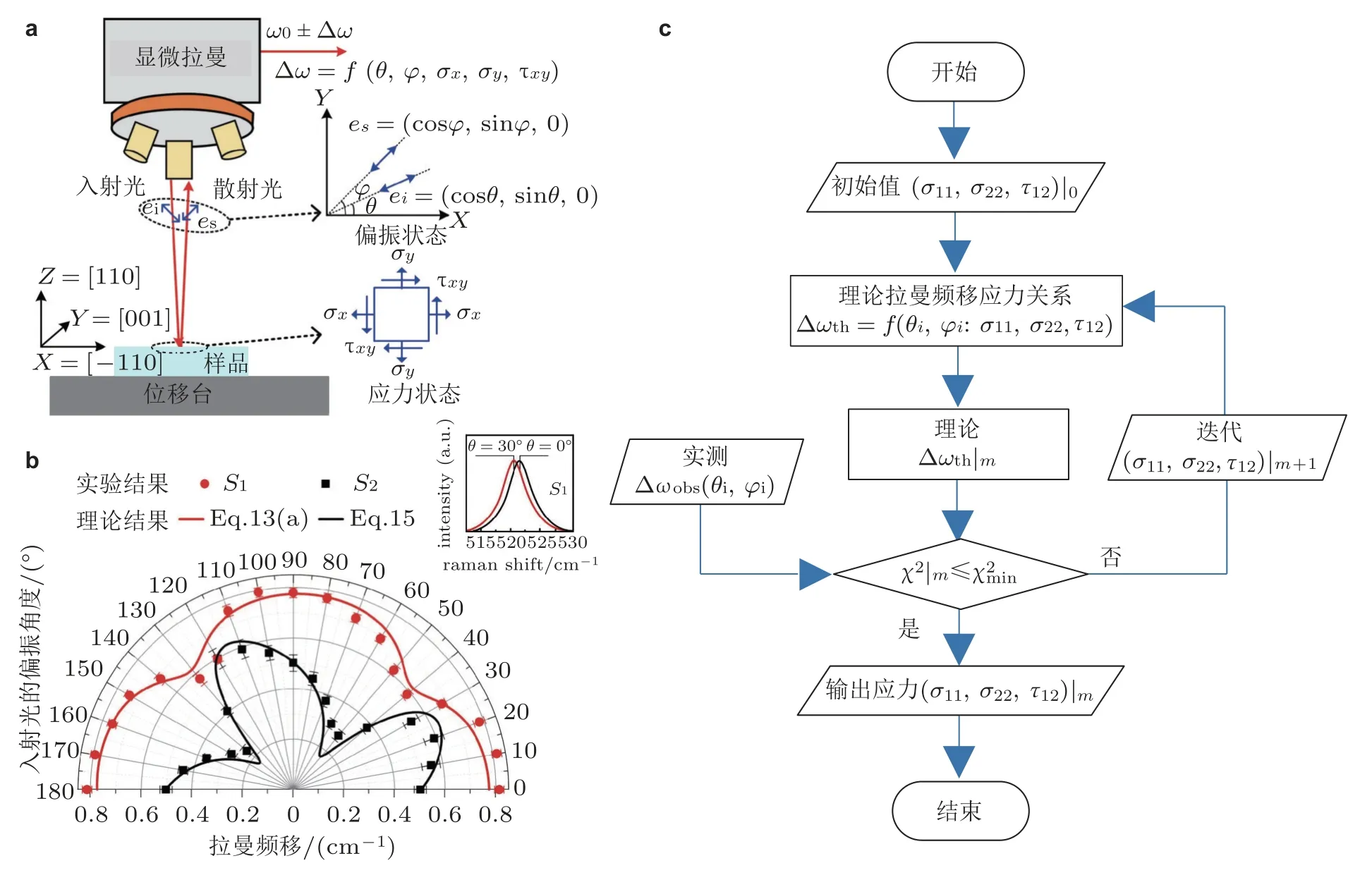
图7 (a) 基于角度分辨拉曼的应力信息提取 (1 1 0) 单晶硅面内应力各分量,(b) 拉曼频移的实验结果与拟合曲线 (Ma et al.2019),(c) 拟合迭代法流程图 (Ma et al.2021b)

除了能够在应力分析中有效提升置信度外,基于角度分辨拉曼的参量精准提取技术还被成功应用于二维材料和光学晶体材料晶向/手性/层数的精准识别、拉曼张量的标定等研究.代表性的工作诸如,Xu B 等 (2021)用角度分辨拉曼分析了二维材料散射的面内各向同性和面内各向异性,并讨论了利用圆偏振拉曼表征材料在三维空间中的方位角等问题.Chang 等 (2017)测得了不同拉伸比下纤维素纳米晶体的角度分辨拉曼强度分布,如图8(a).Wang J 等 (2017)探究了角度分辨偏振拉曼与T’-MoTe2晶向之间的关系.Lin 等 (2020)建立了双折射-线性-二色性模型,定量分析了黑磷在法向和斜向入射角度下的分辨偏振拉曼强度.Li 等 (2020,2021)通过分析和B2g峰的角度分辨拉曼强度,提出了一系列识别黑磷材料晶向的方法,如图8(b)～8(c).Tsukada 和Fujii(2020)结合角度分辨偏振拉曼光谱和多元曲线分辨率 (MCR) 测量了典型铁电晶体PbTiO3的声子参数.此外,Fleck 等 (2020)和Zhang 等 (2022)分别采用角度分辨拉曼精准测量了硒化锑 (Sb2Se3) 薄膜和β相氧化镓 (β-Ga2O3) 的晶向.

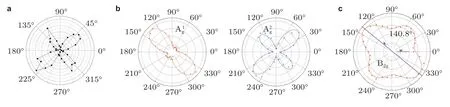
图8 (a)不同拉伸比下纤维素纳米晶体垂直偏振的角度分辨拉曼峰强度(Chang et al.2017),(b)利用垂直偏振构型下 模的角度分辨拉曼峰强度识别黑磷晶向(Liet al.2021),(c) 利用无检偏构型下B2g 模的角度分辨拉曼峰强度识别黑磷晶向 (Li et al.2020)

4 拉曼力学分析主要应用领域与近期代表性成果

显微拉曼光谱对于材料本征和非本征应力都敏感,具有无损非接触地开展原位应力/应变表征的优点,已成为薄膜内应力定量分析、微结构的残余应力/工艺应力在线监控的有效手段.同时,利用激光的透射能力、光学显微的高分辨以及拉曼光谱的应力敏感性,显微拉曼光谱也是目前微纳尺度界面力学实验研究的重要方法之一 (Qiu &Kang 2014,雷振坤等 2015).

拉曼光谱分析能够实现材料结构物性的指纹识别与定量分析,多年来在分析化学、凝聚态物理以及材料学等领域获得了广泛的应用 (Lyon et al.1998,Nafie 2017).受益于de Wolf 简化模型的成果,近二十年来显微拉曼光谱力学分析在残余应力/内应力定量分析方面,取得了许多经典的应用研究成果 (Chen et al.2000,Xu et al.2001,Cappelli et al.2002,Starman et al.2003,Wang et al.2004),所涉及的材料体系包括硅Si (Manotas et al.2000,Chen &de Wolf 2003)、锗Ge (Guo et al.2015)、硅锗合金 (Qiu et al.2016)、金刚石 (Liu et al.2021)、碳化硅SiC(Kollins et al.2018)、氮化镓GaN (Chai et al.2016)、超晶格 (周绪荣等 2008) 等.随着各种精细表征模型和包括偏振、传感、数据分析以及角度分辨拉曼等关键技术的发展,近年来显微拉曼在固体力学及相关领域的研究中发挥了关键的作用.下面将从薄膜材料的内应力检测、微结构的工艺与服役应力表征以及微尺度界面力学研究这三个典型的应用领域入手,论述显微拉曼力学分析的近期代表性成果.

4.1 薄膜材料的内应力检测

薄膜材料是典型的低维材料,其内部应力问题始终是固体力学及相关领域关注的重点,也是实验力学表征的难点.一直以来人们普遍采用各种形貌测量技术,并基于源自梁变形理论的Stoney 公式,来表征薄膜以及薄膜-基底结构的应力.这类方法属于间接手段,故而存在若干局限,特别是面向当今普遍存在的变形复杂的多层膜基结构、整体变形细微但应力量级较大的硬基薄膜或硬基软膜结构、几何形貌/位移变化较大但应力并非引起变形主导因素的软材料薄膜等问题,通过变形测量难以获得或难以准确获得薄膜应力.

对于间接测量难以解决的这些问题,显微拉曼这种应力/应变直接表征的手段则更为适用.相关研究中,Zhao P 等(2021)采用三氟乙酸盐-有机金属沉积技术在SrTiO3和LaAlO3基底上制备了两种YBa2Cu3O7-x(YBCO)薄膜样品,通过拉曼光谱测量给出两个样品YBCO 薄膜的残余应力分别为3457 MPa 和-1265 MPa .如图9(a),Li 等(2016)提出了一种基于拉曼光谱的半定量方法来测量非化学计量氧化铈 (CeO2-δ) 薄膜的应力,同时还可以获得CeO2-δ膜的氧不足信息.Gogoi 等 (2019)研究了激光照射对氧化石墨烯薄膜微观结构的影响,利用拉曼数据计算残余应力、晶粒尺寸和缺陷密度,结果表明薄膜在曝光部分发生了微观结构的变化,其他部分没有发生变化.如图9(b),Huang 等 (2015)利用拉曼表征富硅二氧化硅的薄膜应力,分析了不同O/Si对薄膜结构性能 (晶化度、硅纳米晶体尺寸和残余应力) 的影响.He 等 (2017)利用飞秒激光对生长在Si 衬底上的GaN 薄膜发光二极管 (LED) 表面进行刻蚀,其拉曼实验结果表明,应力与相变在飞秒激光刻蚀过程中起主导作用.

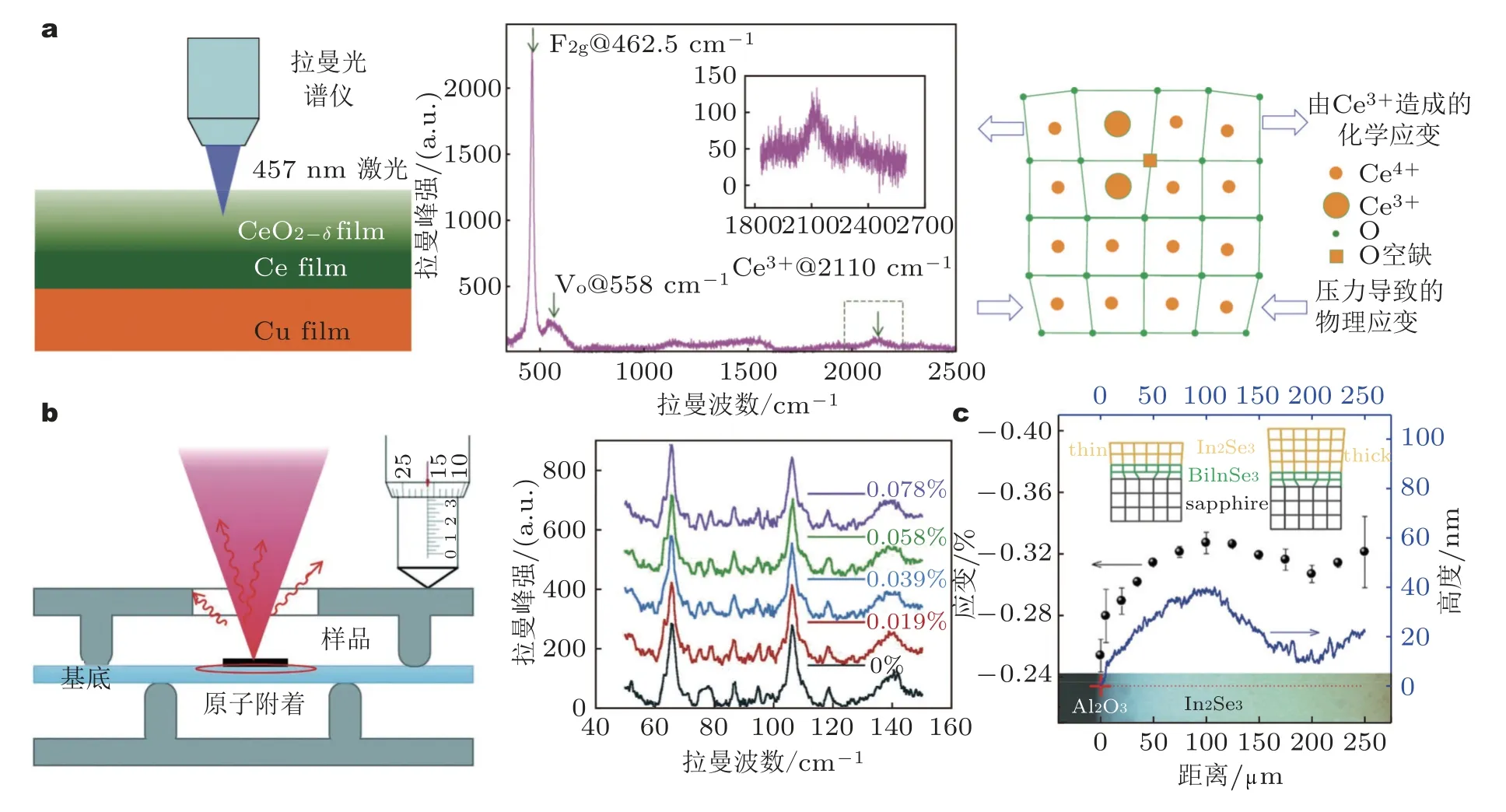
图9 (a) CeO2-δ 薄膜拉曼光谱应力分析,其中左为样品结构示意图,中为样品的拉曼光谱(其插图是2110cm-1 左右范围的放大光谱),右为CeO2-δ晶格因氧空位产生的“化学应变”和外部应力产生的“物理应变”而改变的示意图 (Li et al.2016);(b) Si 衬底Bi2Te3 薄膜的拉曼光谱应力分析,其中左为样品与加载示意图,右为样品在不同温度下的拉曼光谱 (Huang et al.2021);(c)蓝宝石衬底分子束外延生长In2Se3 薄膜应变的拉曼测量 (Li et al.2020)

近年来,伴随各种二维纳米材料的快速发展,显微拉曼光谱已成为研究各种二维纳米材料内应力的主要手段之一.除了石墨烯,新兴的二维纳米材料还包括氮化硼、以MoS2为代表的过渡金属硫化物 (TMDC)、少层黑磷 (磷烯)、以Bi2Se3为代表的拓扑绝缘体等.例如,对于氮化硼材料,Saha 等 (2021)采用显微拉曼研究了在c 面蓝宝石上无碳前驱体外延生长的多层六方氮化硼 (h-BN) 晶格失配和热膨胀失配引起的压缩残余应变.Androulidakis 等 (2018)利用三点弯曲装置加载,原位测量了二至四层六方氮化硼 (h-BN) 在单轴拉伸下的拉曼频移,观察到E2g模分裂 为,而且两到四层厚度的h-BN,其频移对应变的敏感性几乎不变,这与石墨烯形成了鲜明的对比,证明了h-BN 在复合材料应变传感中的潜力.

对于以MoS2为代表的过渡金属硫化物 (TMDCs)材料、少层黑磷 (磷烯) 等,Zhang 等(2019)提出了一种基于拉曼光谱测量二维材料面内热膨胀系数的实验方法,可以解耦热应力、面内热膨胀和面外热膨胀对拉曼峰位置的影响,测量给出了单层二硫化钼 (MoS2) 热膨胀系数.Li 等 (2016)采用一种改进的弯曲技术,对包裹在一层聚甲基丙烯酸甲酯内的超薄黑磷材料沿ZZ 和AR 晶向施加精确的单轴拉伸应变,研究了封装超薄黑磷 (BP) 材料的各向异性拉曼强度和频移响应.Zhang 等 (2016)通过拉曼各向异性测量样品AC 和ZZ 方向的单轴应变,明确地证明了可控单轴应变可以作为一种方便和有效的方法来调谐少层黑磷的电子结构.Wang 等(2015)利用原位应变拉曼光谱研究了单轴应变少层黑磷中晶格振动频率与晶体取向的关系,发现平面外模对近扶手方向的单轴应变敏感,而平面内B2g和模对近“之”字形方向的应变敏感.

对于以Bi2Se3等为代表的拓扑绝缘体,Yan 等 (2015)利用Stokes 和反Stokes 拉曼光谱中的面内以及面外模式,系统地研究了尺寸和应变对拓扑绝缘体Bi2Se3纳米带拉曼光谱的影响.如图9(c),Li 等 (2020)开发了一种通过微拉曼光谱测量分子束外延生长的In2Se3薄膜局部应变的实验方法,利用In2Se3中的A1(LO+TO)峰和Bi2Se3中的峰对应变的敏感性,给出了生长过程In2Se3样品中引入的应力.Niherysh 等 (2021)用拉曼光谱Mapping 技术测量了物理气相沉积在非晶石英和单层石墨烯衬底上合成的不同厚度 (3～ 400 nm)Bi2Se3薄膜以证明生长的均匀性和连续性,并分析了厚度为3 nm,8 nm,11 nm 的Bi2Se3薄膜的内应变.

4.2 微结构工艺与服役应力表征

随着先进材料制造技术的快速发展,各类新型结构与先进功能器件不断涌现.诸如微机电系统 (MEMS,micro-electro-mechanical system)、微电子器件等各类微结构在其制造过程中,其复杂的时序工艺将会引入状态复杂、分布复杂的工艺残余应力,并随着其工艺时序而变化.而在其实际应用中,多场耦合的服役环境也会引起应力场的动态演化.工艺/服役应力不仅关系微结构的可靠性与稳定性,也是影响其功能指标和服役性能的重要因素.开展微结构工艺/服役应力全场动态实验表征是微电子、微机械领域对实验力学提出的共性需求,同时也是实验固体力学领域的关键科学问题.其中,显微拉曼具有高灵敏、无损非破坏、实时原位等重要优势,而快速扫描成像技术的引入更推动了拉曼用于微区应力场定量表征的发展.

de Wolf 团队不仅早期从理论层面推广了拉曼力学分析,其在微结构应力表征方面的应用研究中也取得了诸多引领性的成果,其工作表征了包括晶体管、集成电路中的硅槽隔离结构、硅通孔等微电子器件以及微机电系统在内多种微结构的工艺残余应力 (de Wolf 1999,de Wolf et al.1999,Kosemura &de Wolf 2015).其中,如图10 给出了铜导线通过硅通孔 (TSVs) 后在硅衬底上产生残余应力的三维分布图,应力的三维分布是通过合成沿TSV 不同深度横截面的二维拉曼Mapping 得出的 (Kosemura &de Wolf 2015).

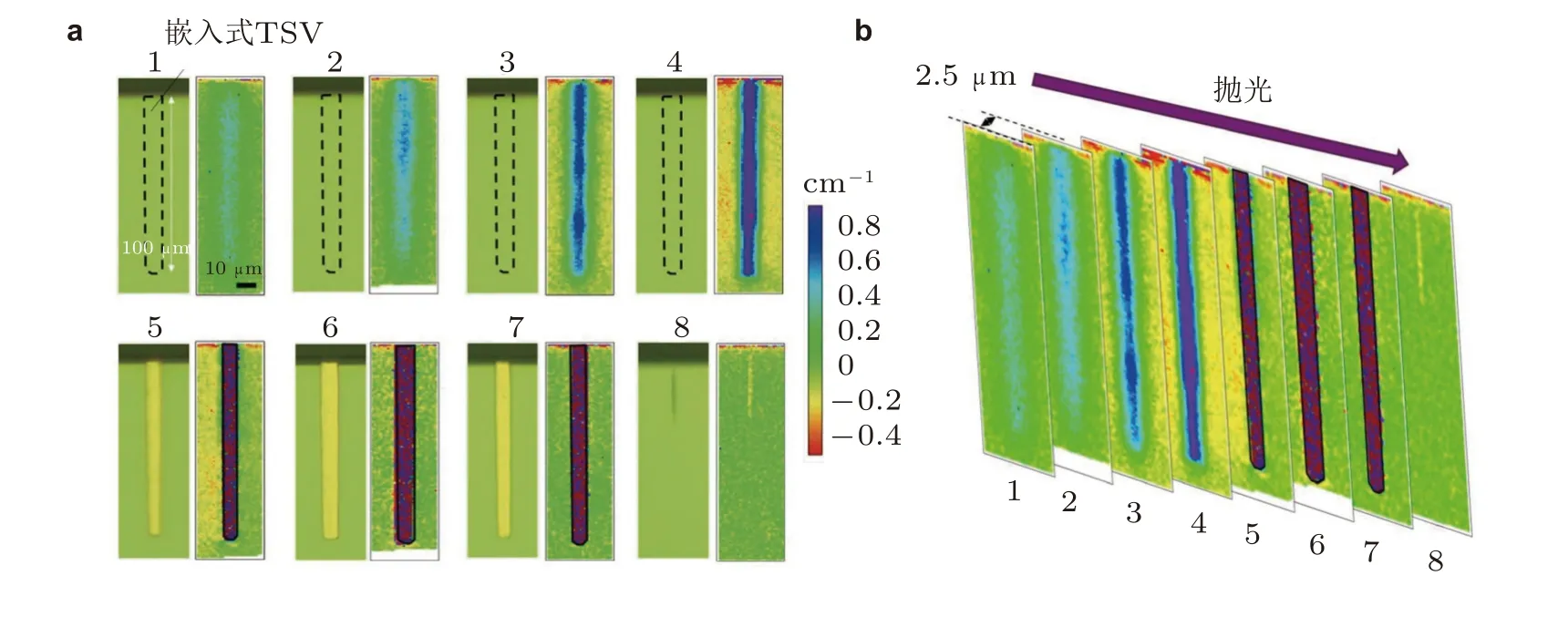
图10 (a) TSV 结构1 到8 横截面的拉曼频移扫描图像,(b) 由(a)中所示扫描图像合并为3D 图像(Kosemura &de Wolf 2015)

近年来,基于显微拉曼扫描成像的应力表征在微系统、微结构的工艺/服役应力场及其演化的实验表征方面取得了诸多有代表性的成果.例如,Zhao 等 (2017)采用显微拉曼配合XRD 研究了退火温度对于熔融纤芯拉伸法制备的锗纤芯纤维内应力与结构性能的影响,其工作通过测量不同退火温度下的拉曼频移和半高宽,给出了退火温度与残余应力和晶体质量的关系,表明通过退火技术可以进一步提高锗纤芯纤维的性能.Rodríguez-Aranda 等 (2017)利用偏振显微拉曼光谱分析了微阵列Ni 结构对硅衬底表面的影响,根据弹性变形理论得出平面内应变的大小为1.4%,这种应变可能会对硅表面的热力学性质产生重大影响.Zhao L 等(2021)通过熔融沉积成型制造具有不同通道和孔径尺寸的聚乳酸 (PLA) 多孔结构样品,采用拉曼光谱技术评估了样品表面产生的残余应力,得到了孔径与表面残余应力的关系,其工作对3D 打印多孔结构的残余应力控制具有指导意义.

在半导体微结构、微系统方面,Chai 等 (2016)在预先成型的SiC 微结构上沉积GaN 薄膜,利用显微拉曼光谱成像分析了不同尺寸和形状的GaN/SiC 微结构阵列中存在的面内残余应力梯度,进一步发现GaN 与SiC 二者残余应力的相互影响机制.Zhang 等 (2017)利用三种相变材料 (Ge2Sb2Te5,Sb2Te3,GeTe) 沉积在不同的绝缘体锗中引起的应变为1%～ 2.5%,表明相变材料能够增强绝缘体上锗迁移率.Wang 等(2019)在微机电系统 (MEMS) 结构中的平行脊和I 型脊区域,使用重叠扫描和图像拼接算法,实现了高分辨的残余应力分布研究.该工作将拉曼实验与仿真分析相结合,发现在MEMS 器件设计中引入带凹槽的折叠结构是抑制残余应力产生的有效方法,如图11(a),从而提高了器件的可靠性.Meszmer 等 (2017)以用于力传感器的MEMS 微结构为研究对象,采用拉曼扫描给出了微结构工作区域的应力分布,并提出了批量分析拉曼光谱数据的算法,实现了低误差且可视化的应力表征,如图11(b).Tingzon 等 (2022)采用显微拉曼光谱表征高对比度光栅可调谐垂直腔面发射激光器 (VCSELs) 中的桥式微机电系统局部应力,结果显示用直流偏压配置静电驱动时在其端点上产生的残余应力越来越大,最高达0.8 GPa.

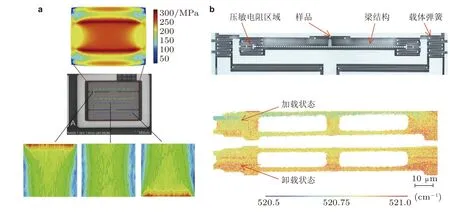
图11 (a) 拉曼分析微机电系统中凹槽结构的残余应力场 (Wang et al.2019),(b) 拉曼测量分析压阻式MEMS 力传感器的残余应力场 (Meszmer et al.2017)

各类新型微结构与先进微器件,往往是处于力、热、电、化、磁等多场耦合或多类型时序变化的服役环境中,从而引入复杂的服役应力.例如先进能源储能结构中,能源转换与存储过程的化学、电化学或者光化学反应引发材料内部微结构产生应力/应变.近年来,拉曼光谱技术在微结构多场耦合环境载荷中的力学分析方面取得了一系列成功应用.Zeng 等 (2016)原位采集了首次恒电流放电过程中硅复合电极的拉曼谱线,结合标定实验给出了硅颗粒应力随时间的演化.Tardif 等(2017)结合拉曼光谱和同步辐射XRD 研究了硅材料应变演化过程,给出了两个充放电循环周期中纳米颗粒内部结构变化.Song 等和Xie 等原位测量了石墨烯材料脱/嵌锂循环过程中拉曼光谱信息,如图12 所示,建立了电化学加载下峰位频移、峰强、分峰等谱线特征参量与晶格结构变形演化的对应关系,给出了前三圈循环中石墨烯电极应变随时间近线性演化曲线,进一步讨论了充放电倍率、微结构、层数等因素对变形与应力的影响,分析了储能过程中的力-电化学耦合机理 (Xie et al.2019,Xie et al.2021,Song et al.2019,Song et al.2022).Rao 等 (2019)结合拉曼光谱和光致发光谱研究了石墨烯/二硫化钼异质结构耦合引起的电荷转移掺杂和应变,并指出热退火条件可调控应变与电荷浓度.Jang 等 (2017)使用离子注入和快速热退火 (RTA) 对化学气相沉积石墨烯进行p 型掺杂,采集了石墨烯材料的拉曼光谱,给出了硼离子掺杂对其应变和电荷浓度的影响,揭示应变和电荷掺杂共同决定了掺杂石墨烯的电学性质.Lee 等 (2019)采用拉曼光谱研究了氧化物生长对多晶铜基板上合成的石墨烯应变和掺杂的影响,给出了应变和电荷浓度随时间的演化信息.Wei 等 (2021)通过拉曼光谱技术研究了附着在二氧化硅衬底上的单层石墨烯面内拉曼声子模的温度依赖性,结果显示热退火温度可以增大石墨烯的温度系数和压应力,在 773 K 退火后,压缩应力高达 2.02 GPa.

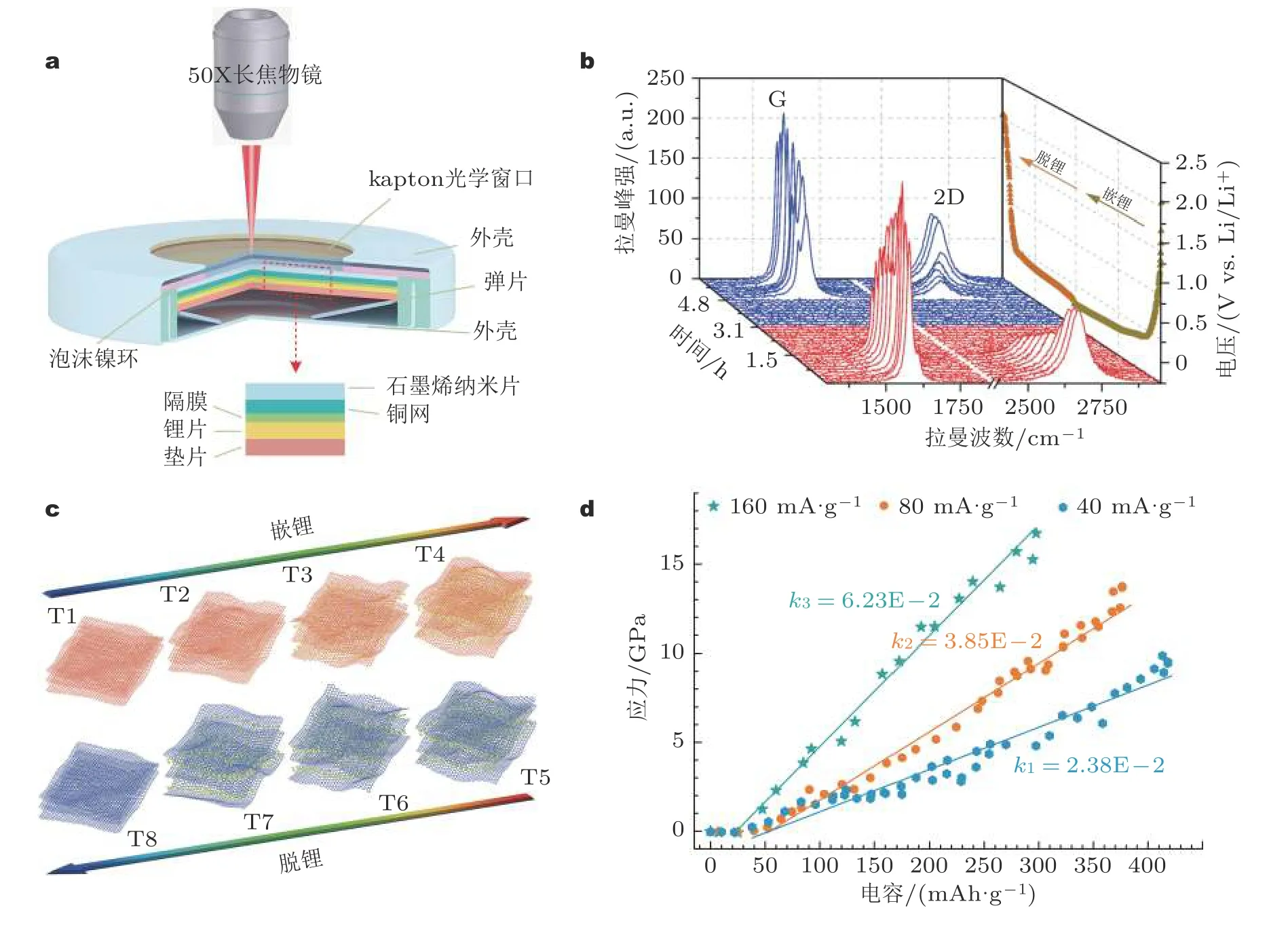
图12 (a) 电极微结构应变测量的原位拉曼实验系统,(b) 多层石墨烯电极在第三次嵌锂和脱锂过程中不同电位下的原位拉曼光谱,(c) 石墨烯电极脱嵌锂过程微结构演化示意图,(d) 不同充放电倍率下石墨烯电极微结构应力演化曲线 (Xie et al.2019,Song et al.2019,Song et al.2022)

4.3 微尺度界面力学实验研究

在微尺度界面力学实验研究方面,显微拉曼光谱是独特而有效的在线、原位实验手段.受益于激光的透射能力以及拉曼光谱的材料“指纹”识别与应力高敏感等特性,显微拉曼能够直接探测复合结构一定深度内部界面区域不同材料的应力/应变信息,无需预处理也不用通过变形场来间接表征,并且也具备较高的时间分辨率 (单测点秒级).

依据目前可检索的文献材料,本领域工作最早源自于英国曼彻斯特大学的Young 教授团队.具体而言,Young 等采用显微拉曼光谱,系统研究了纤维复合材料中短纤维碎断、裂纹尖端桥联、编织结构应变分布等典型界面力学问题,通过原位跟踪纤维的变形与断裂过程,并采用经典剪滞模型给出纤维与基体间界面上的切应力,获得了上述各种典型纤维复合材料的界面力学行为演化规律,从实验力学分析角度为提升复合材料抗断裂能力提供了充分依据,如图13 (Bennett &Young 1998,Young et al.2001,Lei &Young 2001).

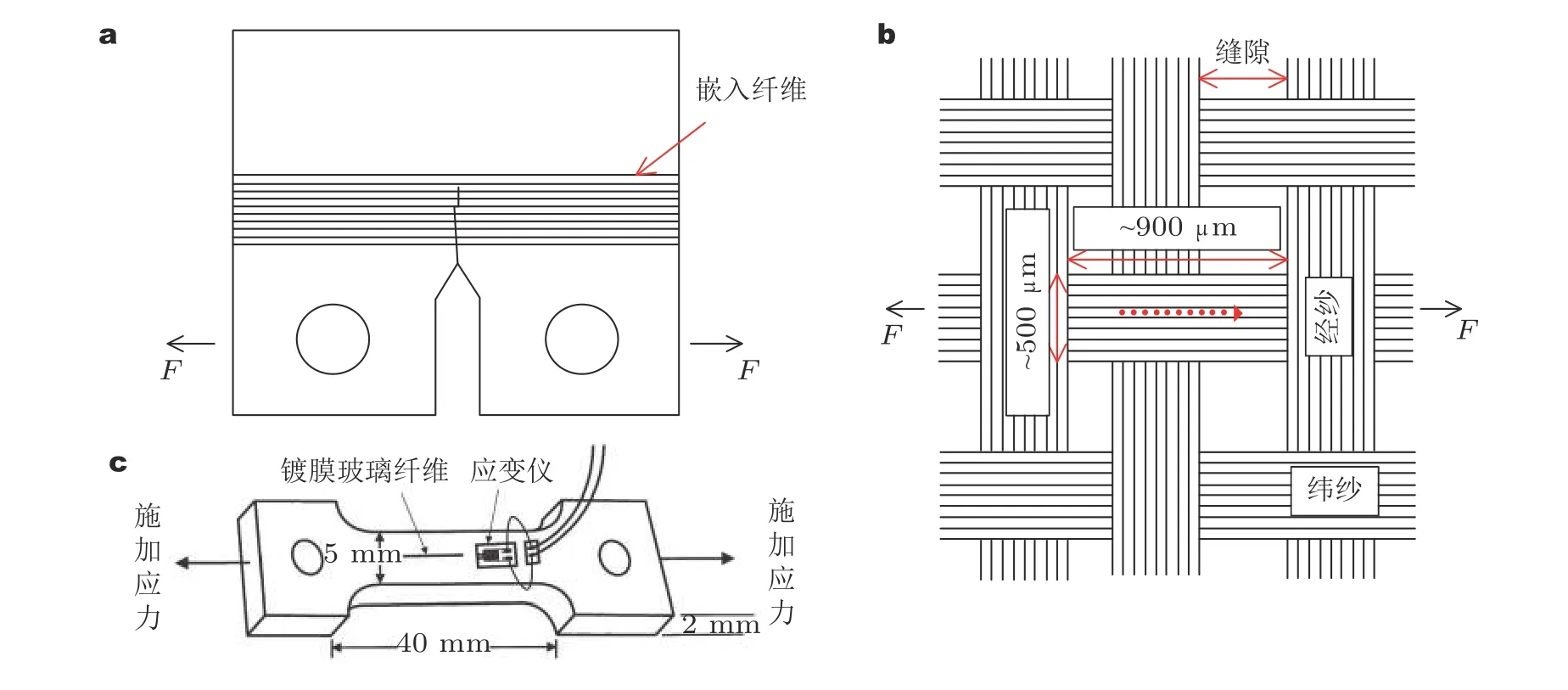
图13 (a) 裂纹纤维桥接实验示意图 (Bennett &Young 1998),(b) 平纹织物单元内的纤维应变拉曼Mapping 测试示意图 (Lei &Young 2001),(c) 内嵌短纤维拉伸碎断实验示意图 (Young et al.2001)

在Young 早期工作的引领下,国际上诸多团队开展了基于显微拉曼的微尺度界面力学实验研究.例如,Moradi 等 (2015)通过显微拉曼测试表明,由于石墨烯薄片与聚偏二氟乙烯 (PVDF)分子链之间存在很强的相互作用,提高了PVDF/G 复合纤维膜的机械强度.Abiko 等 (2019)通过拉曼光谱成像分析了环氧树脂-铝基板复合材料界面附近的残余应力分布.Nance 等 (2021)使用拉曼光谱评估了碳化硅纤维增强陶瓷基复合材料在制造过程各个阶段碳化硅纤维中的残余应力,结果显示编织后和致密化后的残余应力分布为-716 MPa 和-1075 MPa.Verma 等 (2017)在准静态至动态加载 (应变速率从10-2到103s) 下获得了玻璃/环氧复合材料的界面本构响应,使用拉曼光谱技术分析了不同载荷状态下的界面应力,并预测了界面变形行为与应变速率和界面厚度的关系.

国内学者开展的界面力学拉曼实验研究中,Lei 等首先研究了不同浸润角、不同应变水平下纤维微滴结构内界面应力的传递,给出了脱粘界面上切应力的台阶分布,讨论了接触角对微滴内部应力分布的影响,其进一步的深入研究讨论了柔性聚合物涂层影响应力传递的机制 (Lei et al.2013b,Lei et al.2010,Cen et al.2006).此外,Lei 等 (2013a,2013b)还研究了纤维/裂纹的交互作用,分析了纤维搭桥和纤维断裂过程中的界面摩擦滑移转化和重新承载机制.在单纤维的界面行为研究基础上,Lei 等 (2016)建立了多纤维应变测量的显微拉曼光谱原理,通过双纤维拉伸实验验证了该分析技术的可行性.采用这一技术并配合全场光学检测手段,Lei 等得出了单纱拔出、压出过程中织物的应力/应变分布,建立了纱线交织点上的经/纬纱黏着与滑动摩擦的应力传递模型 (Qin et al.2018),给出了织物压出过程中的纱线应力传递规律 (Lei et al.2018).

随着低维纳米材料的发展,显微拉曼光谱成为研究纳米复合材料界面力学行为不可或缺的实验手段.一维纳米复合材料方面,Li 等和Deng 等围绕大直径双壁碳纳米管纤维多尺度力学行为开展实验研究,给出了描述不同尺度上界面行为对宏观弹塑性影响机制的多级界面力学模型(Li et al.2010,Li et al.2012,Deng et al.2014),如图14.Ma 等 (2010)提出了一种碳纳米管网状复合材料结构,引入高分子链段与碳纳米管杂交耦合以抑制碳纳米管束间滑移,并通过拉曼光谱实验表征了材料界面区域应变传递效率.

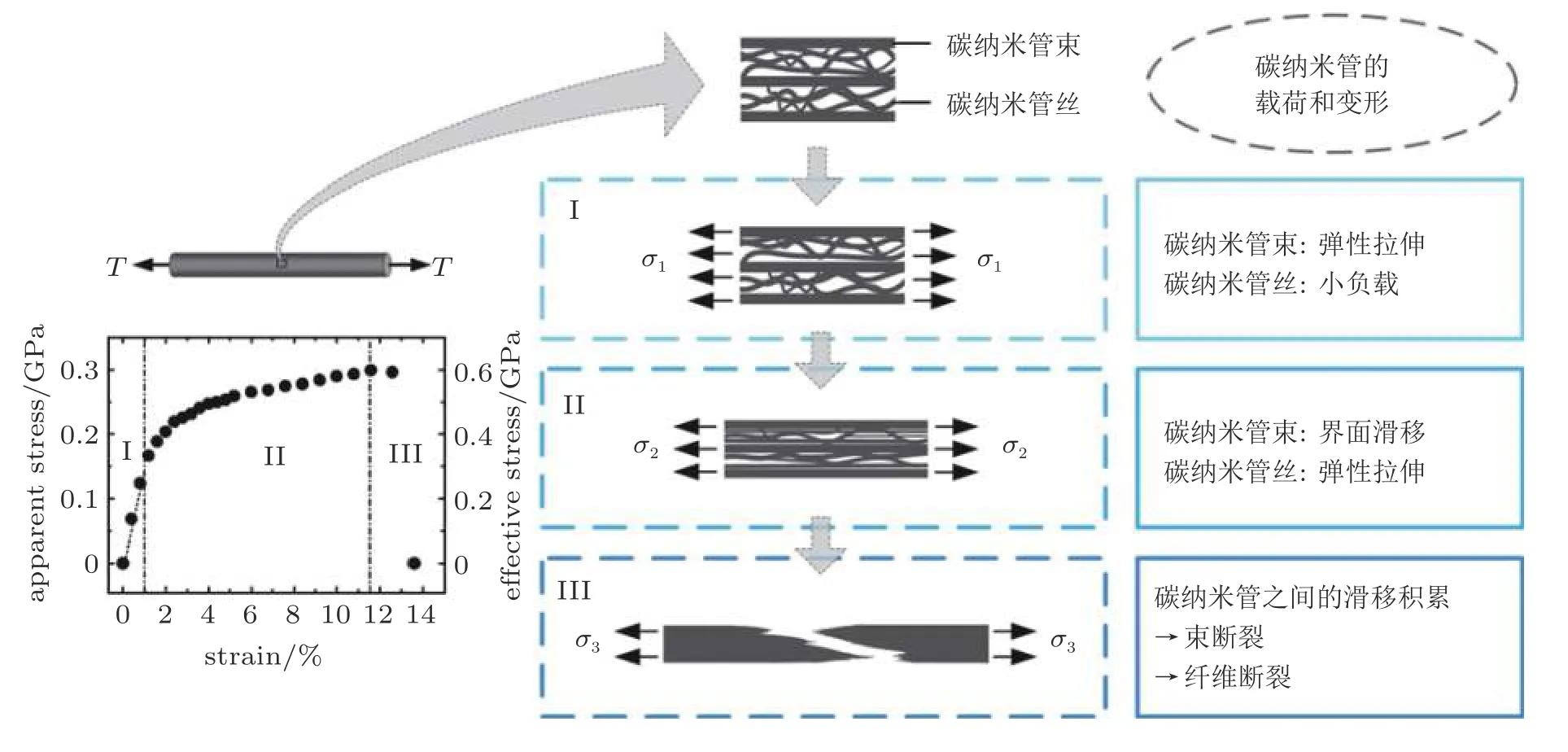
图14 拉伸载荷下碳纳米管纤维多尺度结构的承载与变形特性 (Li et al.2012)

二维纳米复合结构方面,Xu 等和Dou 等研究了柔性基底上单层/双层、单晶/多晶石墨烯的界面变形传递,该工作设计了宏-细-微7 种不同长度系列实验,发现石墨烯与柔性基底间的界面性能存在显著“尺寸效应”新现象,提出了界面强度两个尺寸效应阈值.该工作描述了尺寸对界面力学性能影响规律,揭示了纳米材料界面力学参量“测不准”现象背后的机理,从而将国际不同团队实验结果相互矛盾引向新科学规律的相互印证 (Xu et al.2016,Dou et al.2018,Xu et al.2019),如图15.Du 等使用拉曼Mapping 技术全场定量表征了二维石墨烯在柔性基底上的初始冗余应变,并发现渐增式预循环加卸载策略可有效地均匀化石墨烯初始冗余应变,通过量化对比这一过程中的界面剪切强度,揭示了其增强界面力学性能的内在机制,即预循环处理策略减小了碳原子与基底的距离,改善了界面共形程度,如图16 所示 (Du et al.2018,Xu C et al.2021).Bousige 等 (2017)使用拉曼光谱研究SiO2、金刚石和蓝宝石基底与石墨烯双轴压缩应变传递的极限,结果表明临界应力和应变传递效率取决于基底的性质.Li 等 (2019)使用拉曼光谱研究了PMMA 基底上褶皱和折叠状石墨烯的界面应力传递,并量化了界面应力传递效率.Hu 等 (2019)采用拉曼光谱研究对比了石墨烯不同湿度环境下应变松弛,发现具有水合界面应变势指数级松弛.

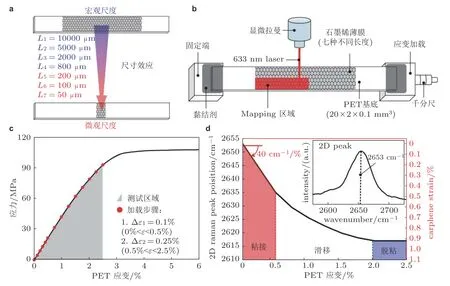
图15 (a) 七个不同长度的石墨烯/PET 试件示意图 (不按比例);(b) 实验装置示意图 (显微拉曼系统和石墨烯/PET 试件,不按比例);(c) PET 基体的应力-应变曲线;(d) 加载过程中石墨烯中心点处的应变与PET 应变的关系曲线,其中曲线以下阴影区域分别表示黏附 (红色)、滑动 (白色) 和剥离 (蓝色) 阶段 (Xu et al.2016)

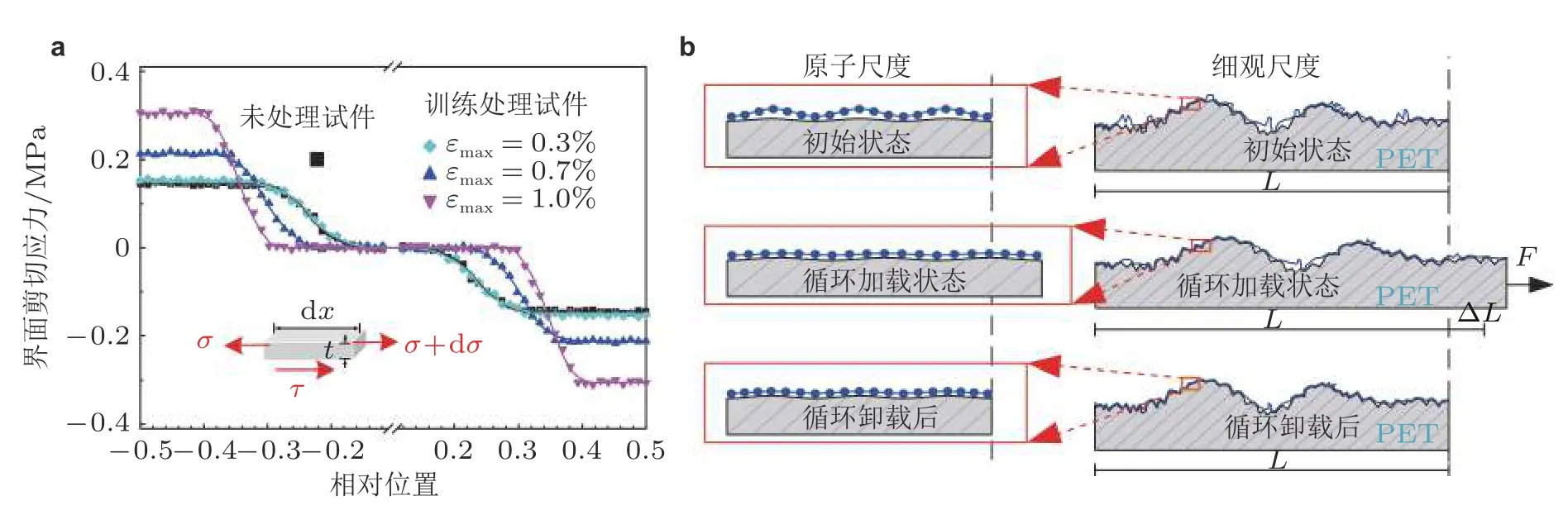
图16 (a) 使用显微拉曼分析三种循环载荷训练后与未循环的石墨烯/PET 试件在界面脱粘后界面剪应力沿拉伸轴方向的分布,(b) 循环载荷训练改善界面贴合度的原子尺度和细观尺度示意图 (Du et al.2018)

近年来,拉曼光谱测量成功应用于二维材料同质结构和异质结构的界面实验分析.同质结构方面,Wang 等 (2017)基于微尺度气泡加载分析了双层石墨烯的层间力学行为,如图17(a).Liu等 (2022)测量了柔性基底上同位素双层石墨烯间的界面剪切耦合,如图17(b).Androulidakis 等(2020)通过测量毫米尺度双层石墨烯的拉曼峰频移,评估石墨烯超润滑状态下的层间剪切应力.

图17 使用显微拉曼手段分析双层石墨烯层间切应力.(a) 气泡加载 (Wang G et al.2017),(b) 基底加载 (Liu et al.2022)

在异质结构拉曼应力分析方面,Li 等 (2017)利用超低频拉曼光谱测量石墨烯/MoS2范德华异质结构中的界面相互作用.Rao 等 (2019)通过对石墨烯/MoS2拉曼特性峰的相关性分析发现热退火过程中由界面应力传递引入压缩应变.Du 等 (2022)提出拉曼与荧光谱协同测量的方法,原位分析了典型的二硫化钼/石墨烯异质结构中各层内的应力演化过程以及各层间剪切强度,如图18.Nguyen 等(2021)利用低频拉曼光谱研究了2H-MoTe2/hBN 异质结构的层间振动模式,发现1～ 4 层厚度MoTe2能够观察到的低频拉曼模中,剪切模在异质结构中保持不变,但呼吸模在异质结构中发生了剧烈的变化;利用线性链模型对呼吸模态频率进行分析,得出2H-MoTe2与hBN 之间的界面力常数为3.77 × 1019N·m-3.Xing 等 (2023)围绕柔性基底石墨烯/二硫化钼异质结的界面力学行为开展显微拉曼与显微荧光相结合的原位表征,基于实验结果提出了有限弹性界面应变传递模型,揭示了异质结构相互间及其与基底间界面的竞争机制.

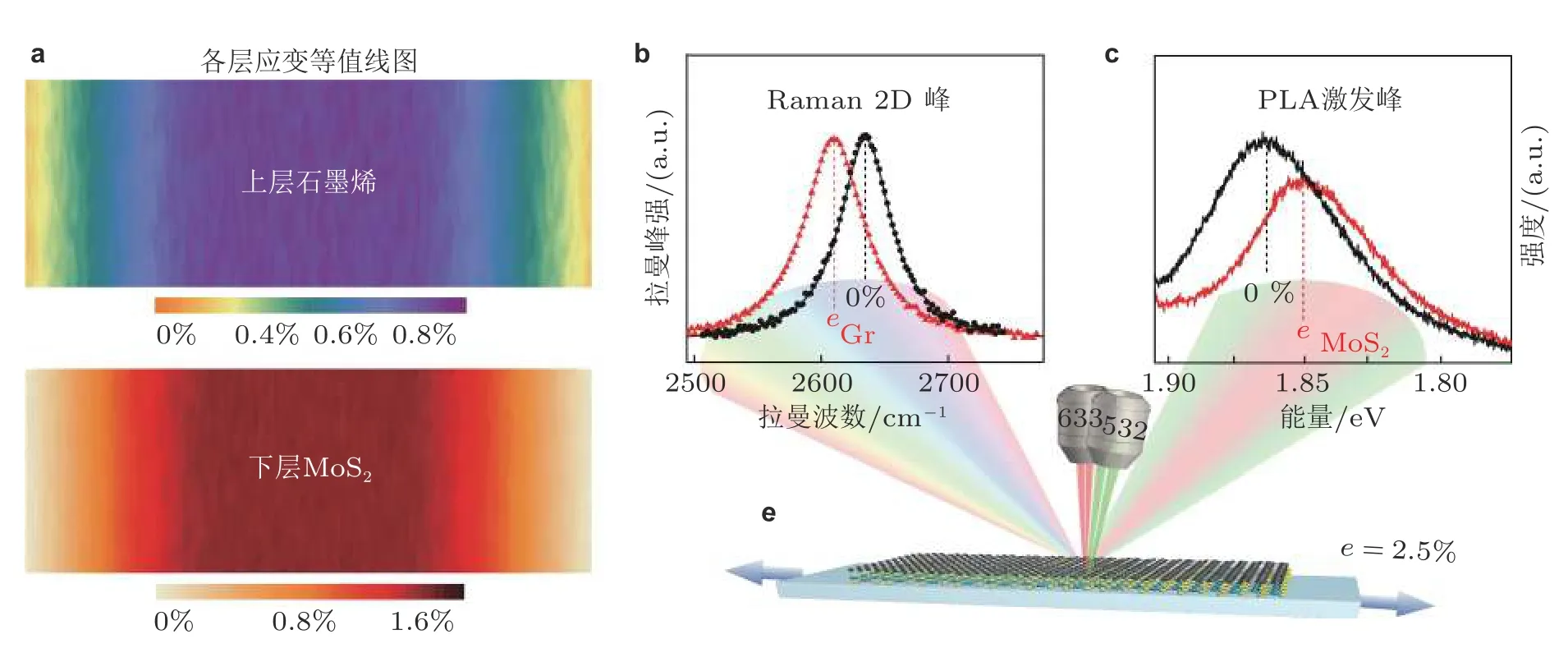
图18 石墨烯/MoS2/PET 异质结构拉伸载荷下的原位拉曼和荧光光谱分析 (Du et al.2022).(a) 当衬底被拉伸至 2.5% 时异质结构中每一层的应变云图,(b) 633 nm 激光激发拉曼光谱定量表征上层石墨烯的应变,(c) 532 nm 激光荧光光谱定量表征下层MoS2 的应变

5 结论与展望

本文围绕基于显微拉曼光谱的力学分析,综述了近年来其在实验理论与关键分析等方法学研究中取得的代表性进展,并列举了该方法在半导体器件、微机电系统、储能器件等工程领域以及先进膜基结构、纳米复合材料等力学交叉前沿方向的部分典型应用.随着固体力学及相关领域科学与工程问题研究对微尺度力学测试需求的日益提升,围绕显微拉曼力学分析方法及其应用研究,预期未来的发展趋势如下.

拉曼力学方法学研究方面: ①面向内部力学参量的实验分析,发展面向复杂材料体系的三向应力 (各分量) 精准表征的实验理论模型及相关实用技术;②针对异质、多级结构精细力学表征,将拉曼与电子或探针显微平台以及多场加载相结合,发展多尺度物-化-力原位协同表征技术及新型联用仪器;③为提升光谱力学测量与分析的可视化,发展适合于力学实验研究采用的可视化“谱像”分析方法.

拉曼力学应用需求方面: ①面向柔性电子多层膜基结构、声子晶体超材料、手性纳米同质/异质结构、拓扑绝缘体等先进材料,通过开展显微拉曼光谱以及其他技术相结合的实验应力分析,发现力学以及交叉学科的新现象、新规律;②针对微光电子、三代半导体、涂层结构、新能源电池等各种先进结构与器件,采用光谱力学测量手段,探索解决其中的工艺残余应力演化以及极端环境下的服役应力管控问题.

致 谢国家杰出青年科学基金 (12125203),国家重大科研仪器研制项目 (11827802),国家自然科学基金国家自然科学基金创新群体项目 (12021002).