钴基高温合金GH188板材的屈服行为研究
门明良,孟宝,朱宇,石佩珏,刘红梅
钴基高温合金GH188板材的屈服行为研究
门明良1,孟宝1,朱宇2,石佩珏3,刘红梅3
(1.北京航空航天大学 机械工程及自动化学院,北京 100191;2.中国航空发动机研究院,北京 101304;3.中国航发动力股份有限公司,西安 710021)
研究钴基高温合金GH188板材在不同应力状态下的屈服行为,并确定适用的屈服准则,为工程应用提供科学指导。通过开展不同方向的单向拉伸试验得到基本力学性能参数,以轧制方向为参考方向,利用其真实应力-应变曲线标定Ludwik本构模型参数;根据国际标准设计十字形试件,利用ABAQUS软件对其等双拉加载进行有限元仿真,然后基于设计的试样对GH188高温合金板料进行不同载荷比例下的双向拉伸试验,并获取屈服点;结合以上数据,采用Mises、Hill48、Barlat89和Yld2000-2d 4种屈服准则对屈服轨迹、值和应力值进行预测。等双拉过程中,十字形试件中心区应力分布均匀且无切应力,表明试样的设计是合理有效的;4种屈服准则对试验屈服轨迹的平均预测误差相差不大,为(2±0.5)%,但整体而言,Hill48-的预测误差最大,Hill48-和Barlat89屈服准则呈现相似的预测能力,误差约为20%,Yld2000-2d屈服准则预测精度最高,综合误差仅有2.41%,远远小于其他3种屈服准则的预测误差。钴基高温合金GH188板材具有明显的各向异性,Yld2000-2d屈服准则可以精确地描述该材料在复杂应力状态下的屈服行为。
高温合金;GH188;十字形试件;屈服准则;屈服轨迹
GH188是Co–Ni–Cr基固溶强化型变形高温合金,相比镍基高温合金具有更优异的耐热疲劳、耐热蚀和焊接性能,可以在极高的温度(730~1 100 ℃)下进行服役,已广泛应用于航空发动机和燃气轮机领域[1-2]。目前,对GH188高温合金已经开展了大量的研究,主要集中在寿命分析[3-4]、硬化[5]和钎焊行为[6]、热塑性变形行为和动态再结晶[1-2,7]等方面。而这些成果几乎都是对GH188高温合金在单向应力状态条件下的研究,对材料在不同方向或者多轴应力状态下的力学行为研究还鲜见报道。
金属板材塑性成形通常是在复杂应力状态下沿着不同路径成形的,会受到多轴载荷条件的影响,单轴测试无法检测到多轴应力和应变,不能准确描述GH188合金这种各向异性材料在复杂应力状态下的力学行为。因此,不仅需要在单轴拉伸下,而且需要在多轴应力状态下,例如更接近实际物理状态的双轴拉伸[8],来研究金属板材的机械性能,以求能更准确地表示钣金的塑性变形行为。
可以通过十字形试件的双向加载试验来研究材料在复杂应力状态下的塑性变形行为,这也是众多学者和科研机构公认的行之有效的方法[9-10]。该试验的优势在于能独立控制两个方向上的负载,也就是说,为获得材料在双向拉伸应力状态下的任意屈服点,可以改变两个方向的载荷比,从而更全面地研究材料在双向应力状态下的屈服行为[11]。Shiratori和Ikegami最早提出了双轴拉伸试验技术[8],随后,许多研究人员(如Kulawinski等[12]、Leotoing等[13]、万敏课题组[14-15]等)开发了双轴拉伸技术来研究金属板材在复杂应力状态下的力学性能[10]。
陈雷等[11]对定向凝固高温合金IC10进行了双向拉伸试验,得到试验屈服轨迹,并采用不同的屈服准则对其进行了理论预测;结果表明,Banabic–Balan和Barlat89屈服准则可以较好地描述IC10高温合金的屈服行为。Shi等[16]探索和讨论了复杂加载路径下SUS304不锈钢箔的屈服行为,利用Yld2000–2d屈服准则和混合硬化模型对其初始和后继屈服轨迹进行了精确预测。Zheng等[17]研究了超薄SUS304不锈钢板在双轴比例加载条件下的尺寸依赖性变形硬化行为及纯铜箔的屈服演化[18],理论预测结果均与试验结果具有良好的一致性。Cai等[19]提出了一个具有可变指数的修正Yld2000–2d屈服函数来预测DP钢系列和6016系铝合金的屈服演化行为,取得了良好的效果。江培成等[20]以2A16铝合金板材为研究对象,基于所设计的十字形试样,进行了5种比例加载条件下的双向拉伸试验,研究了2A16铝合金板材在双向加载时的材料力学性能。Kotkunde等[21]使用Barlat89和Hill 48屈服准则研究了Inconel625高温合金的各向异性屈服行为,结果表明,与Hill48屈服准则相比,Barlat89屈服准则在屈服轨迹、各向异性系数变化和屈服应力变化方面的预测能力更准确。Iftikhar等[22]报道了退火AZ31镁合金在不同变形水平下的屈服轨迹演化,其初始屈服轨迹与von–Mises屈服准则的预测结果显著不同,并观察到明显的拉压不对称。Hu等[23]通过耦合Poly4屈服准则和非二次屈服准则构造了关联流动屈服准则,并对AA3104–H19和AA5042–H2的屈服轨迹进行了理论预测,结果表明,预测结果和试验结果吻合较好,该屈服准则已在隐式有限元程序AutoForm R8的开发版本中实施。从以上研究中可以看出,国内外对钢、铝、镁、钛等合金材料的各向异性屈服行为的研究比较火热,对高温合金屈服行为的研究较少,因此,有必要对GH188高温合金板材在单向和多向应力状态下的力学屈服行为进行研究。
文中首先通过不同方向的单向拉伸试验得到基本力学参数,并标定Ludwik本构模型参数,然后基于国际标准和有限元仿真设计十字形试件,并进行双向拉伸试验以获取高温合金GH188板材的屈服轨迹,进而采用4种宏观屈服准则对GH188高温合金板材屈服行为进行理论预测并评估其适用性,为其在航空航天领域更加合理高效的应用提供理论基础。
1 试验方法
1.1 单向拉伸试验
本研究使用的材料是厚度为1.1 mm的高温合金GH188板材,为了获得真实的应力–应变关系和基本力学性能参数,在MTS电子拉伸试验机上进行单轴静态拉伸试验。单轴试验试样的形状和尺寸设计基于《金属材料拉伸试验第1部分:室温试验方法》(GB/T 228.1—2010)[24],将高温合金板材沿与轧制方向成0°(Rolling Direction,RD)、45°(Diagonal to Rolling Direction,DD)、90°(Transverse Direction,TD)方向加工成图1所示的形状及尺寸,每组试验重复进行3次后取平均值,得到的真实应力–应变曲线如图1所示。初始屈服应力为0.2%塑性应变所对应的应力,根据试验曲线计算获得的基本力学性能参数如表1所示。

图1 不同方向的GH188真实应力–应变曲线
表1 GH188基本力学性能参数
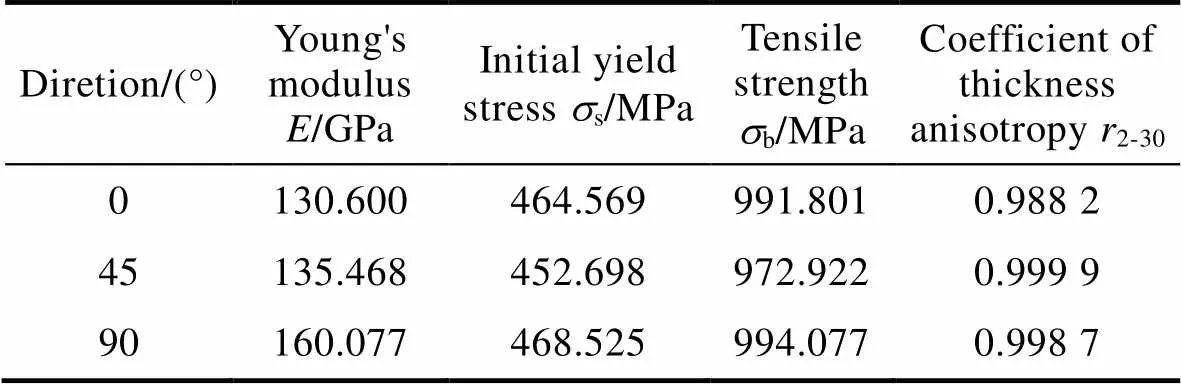
Tab.1 Basic mechanical property parameters of GH188
采用Ludwik本构模型,对轧制方向单向拉伸真实应力–真实塑性应变曲线进行拟合,并确定模型中的材料常数,为十字形试件优化设计模拟提供基础,Ludwik模型形式见式(1)。
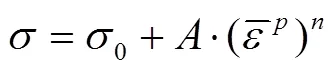
1.2 十字形试件设计
十字形试件优化设计是双向拉伸试验最重要的环节之一,直接关系着试验结果。许多研究已经调查和讨论了用于双轴测试的十字形试件的适当形状,双轴拉伸试件的标准几何形状仍然是一个热门研究课题。许多研究工作提出了2个主要的设计先决条件:十字形试件中心区的双向拉应力状态分布均匀,测量区无切应力;双拉变形区域内的应变最大化[25]。
本研究采用万敏团队设计制造的双向加载试验系统[15],根据金属板料双向拉伸国际标准(ISO 16842: 2014)[26],参考之前学者的研究[8,14,17],设计并优化臂上开缝型十字形试件的几何尺寸,以适应该双向拉伸试验机的钳口宽度、夹钳闭启尺寸等相关结构尺寸,并保证中心区域尽可能处于双向拉伸应力状态,所设计的十字形双拉试件几何形状及尺寸如图2所示。

图2 十字形试件形状及尺寸
合理的试件形状及尺寸对于保证试验应力的测量准确度、提升所获得的试验屈服轨迹的精度等方面都有明显的优势。因此,使用Abaqus软件对所设计的十字形试件进行等双拉有限元模拟,通过分析十字形试件中心区域内的应力分布情况来确保所设计的十字形试件的有效性与合理性。考虑到材料性能及边界条件的对称性,有限元模型为1/4模型,采用S4R壳单元,厚向积分点为5个,中心区域单元尺寸为0.5 mm,臂上区域单元尺寸为1 mm。计算所使用的求解器为Abaqus/Standard。在数值仿真过程中,采用上述本构模型和Mises屈服准则,将15 kN的载荷分别施加于2条臂部的末端,而十字形试件中心区域的边界采用对称约束进行固定,如图3所示。
参考国际标准中双向拉伸试验的应变测量位置为(0.35±0.05)(为臂宽,=24 mm),该十字形试件的应变测量范围确定为距离中心线长度8 mm的中心区域,将应变测量范围内的主应力11和12从数值模拟仿真结果中提取出来,如图4所示。十字形试件在中心区的测量区域应力分布比较均匀;其中心区剪应力很小,最大值小于6 MPa,仅为正应力分量的1%,符合测量区无切应力的要求,可以认为处于较为理想的双向拉伸主应力状态,因此,所设计的十字形试件合理有效。

图3 等双拉模拟有限元模型
1.3 双向拉伸试验
基于前面所设计的十字形试件进行双向拉伸试验。为了获得GH188板料主应力空间内的试验屈服轨迹,进行包含9个固定载荷比的双轴拉伸试验。将载荷比定义为RD方向载荷(F)与TD方向载荷(F)的比例,即F:F为4:0、4:1、4:2、4:3、4:4、3:4、2:4、1:4和0:4。需要注意的是,载荷比为4:0和0:4的双轴拉伸试验分别由上述提到的沿0°方向和90°方向的单向拉伸试验代替。每一种材料状态和载荷比下的双向拉伸试验重复进行2~3次,所得不同比例加载条件下的真实应力–应变曲线如图5所示。
2 屈服准则理论
为了系统评估现有宏观屈服准则对于高温合金板材GH188的适用性,选用4种宏观屈服准则,包括各向同性的Mises屈服准则,各向异性的Hill48、Barlat89和Yld2000–2d屈服准则[27],通过对比理论屈服轨迹与试验屈服点来分析屈服准则的有效性。
1)Mises屈服准则。von Mises在1913年提出了二次各向同性屈服准则,平面应力状态下的数学表达式见式(2)。

2)Hill48屈服准则。Hill基于上述理论,在1948年提出了具有各向异性性质的Hill48屈服准则,假设材料的各向异性主轴平行于应力张量主轴。在平面应力状态下,其表达式如式(3)所示。

式中:F、G、H、N为材料的各向异性系数。可以通过变形各向异性数据,即与轧制方向成0°、45°、90°方向的r值(、、)求解,如式(4)所示。
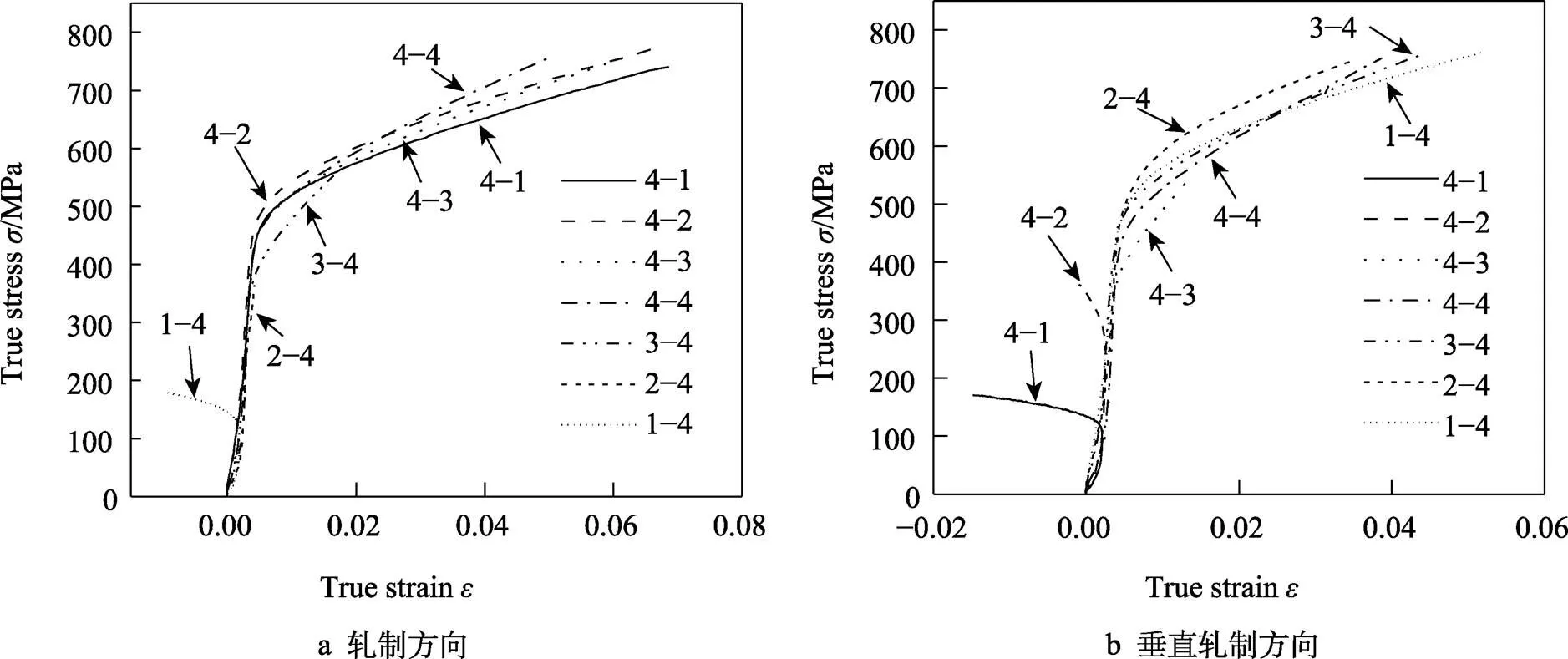
图5 不同比例加载条件下的真实应力–应变曲线
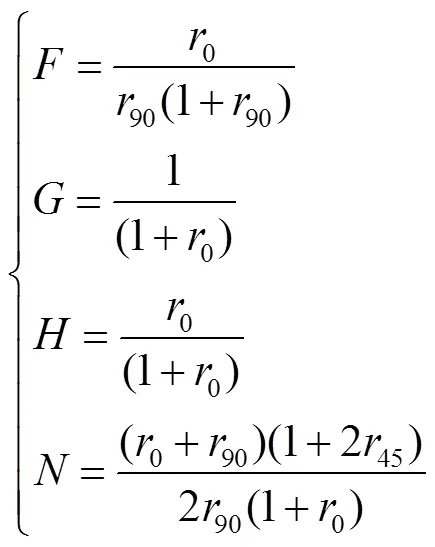


当3=3=3时,Hill48屈服准则不再具有各向异性,且与Mises屈服准则等价。
3)Barlat89屈服准则。1989年,Barlat和Lian在Hosford的基础上加入剪应力,为了描述金属板材面内各向异性行为,提出了Barlat89屈服准则,见式(6)—(7)。
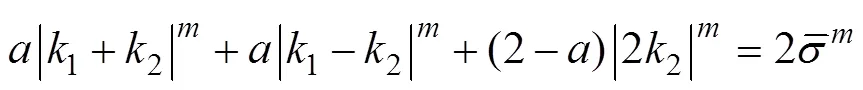
其中,
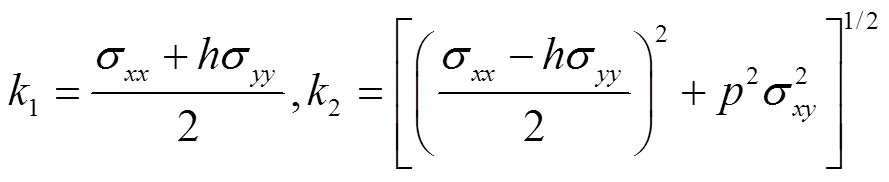
4)Yld2000–2d屈服准则。基于各向同性塑性等效(IPE)思想的启发,Barlat等在Hershey–Hosford准则中通过对应力张量引入2个线性变换,进而提出Yld2000–2d屈服准则。该屈服准则可以描述平面应力状态下金属板料的屈服行为,如式(8)所示。
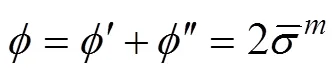


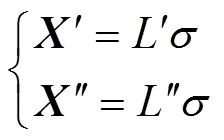
其中,

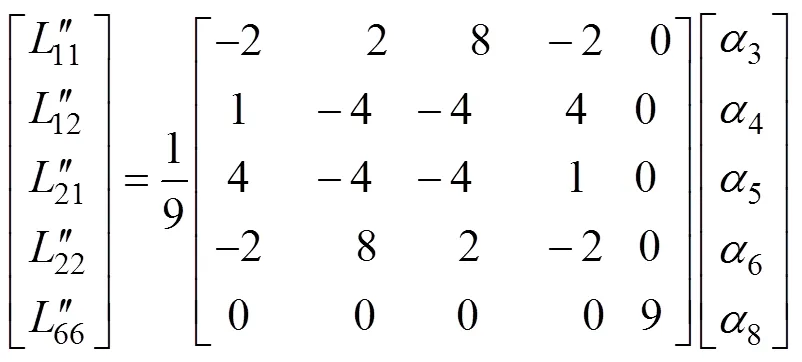
式中:与Barlat89屈服准则中的含义相同。Barlat建议,对于体心立方(BCC)结构的金属,取值为6;对于面心立方(FCC)结构的金属,取值为8。文中所研究的高温合金GH188板材属于FCC结构,因此,取值为8。1~8是Yld2000–2d屈服准则的8个独立各向异性系数,可以由8个材料特征参数进行确定:0、45、90、0、45、90、b(460.119 MPa)和b(等双拉应力状态下塑性应变增量比d2/d1,0.717 3)。
3 基于不同屈服准则的预测结果
3.1 理论屈服轨迹的预测结果
以RD方向单拉试验屈服点作为理论屈服轨迹的基准点,通过编写的MATLAB程序可以计算得到4种屈服函数的系数,进而可以得到以上4种不同屈服准则所预测的高温合金板材GH188的理论屈服轨迹,得到的屈服准则参数如表2—4所示。
表2 Hill48屈服准则的求解参数

Tab.2 Solving parameters of Hill48 yield criterion
表3 Barlat89屈服准则的求解参数

Tab.3 Solving parameters of Barlat89 yield criterion
表4 Yld2000-2d屈服准则的求解参数

Tab.4 Solving parameters of Yld2000-2d yield criterion
根据上述得到的双向拉伸应力–应变曲线和单位体积塑性功相等原理[17],可以得到试验屈服点,图6给出了高温合金材料GH188的理论屈服轨迹,并与试验结果进行了对比。基于不同的理论模型预测的理论屈服轨迹表现出较大的差异,为了能够定量评估屈服准则对试验屈服轨迹的拟合精度,引入误差函数,即

式中:σ1i和σ2i分别为沿RD和TD方向的屈服实验点对应的主应力;Li是试验屈服点与相应载荷比下理论预测屈服点之间的距离;n代表屈服轨迹上屈服点数量(n=9)。根据引入的误差函数,统计了试验值与不同屈服准则所预测的理论屈服轨迹之间的误差,如图7所示。
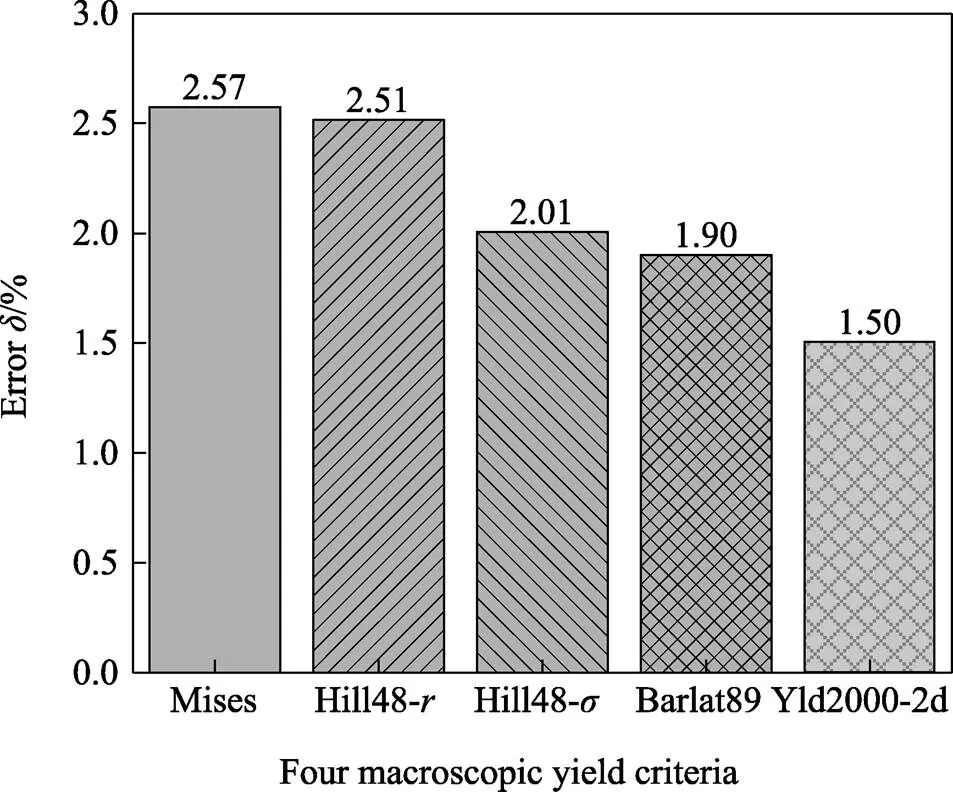
图7 不同屈服准则对GH188屈服轨迹的预测误差
采用不同参数求解方法的Hill48屈服准则的理论预测结果也具有一定的差异性,其中,Hill48-表示的是采用厚向异性指数(值)进行参数求解的Hill48屈服准则,Hill48-表示的是采用不同方向的应力值()进行参数求解的Hill48屈服准则。从图6中可以看出,GH188高温合金板材表现出明显的各向异性,而具有各向同性的Mises屈服准则不能描述该试验结果。Hill48-屈服准则与Mises屈服准则预测结果几乎完全重合,结合表2可知,此时Hill48-屈服准则4个参数的关系非常接近于3=3=3,这种情况下,Hill48-屈服准则等价于各向同性的Mises屈服准则,因此,两条理论屈服轨迹几乎完全重合;当采用应力值求解Hill48屈服准则参数时,4个参数也比较接近上述关系,因此,Hill48-所预测的屈服轨迹与Mises和Hill-屈服准则预测的屈服轨迹相差不大。对Barlat89屈服准则而言,虽然其系数也是通过值来进行求解的,但是依然可以较为准确地描述初始屈服轨迹,预测效果优于Hill48–屈服准则。Yld2000–2d屈服准则考虑的参数较多,包含了几个关键方向的应力值和值,预测得到的屈服轨迹更接近试验结果,可以准确描述其屈服行为。
以等双拉屈服点为界,将屈服轨迹分为上、下两个半区。在屈服轨迹的上半区,Mises和Hill48屈服准则预测结果较好,接近各向同性,理论屈服轨迹和试验结果接近,但是与加载比例为3:4时的屈服点偏差较大;在屈服轨迹的下半区,两个屈服轨迹的预测效果较差,理论预测值高估了屈服应力,导致预测结果的误差最大,如图7所示,平均误差在2%以上。而Barlat89和Yld2000–2d屈服准则在屈服轨迹的上半区预测结果较为接近,但仍与试验结果存在一定的偏差,并且与在加载比例为2:4条件下的屈服点偏差最大;而在下半区,Yld2000–2d屈服准则所预测的屈服轨迹比Barlat89的预测结果更接近试验值,预测误差更小,仅有1.50%。综上所述,GH188高温合金的屈服轨迹关于等双拉线具有非对称性,表现出明显的各向异性,在这4种屈服准则中,Yld2000–2d屈服准则能够更好地描述预测高温合金GH188板料的初始屈服轨迹。
3.2 r值和应力值预测结果
通过比较值和值的预测与试验结果,也可以评估屈服准则的性能。由于Mises屈服准则和Hill48–屈服准则均表现出各向同性的性质,因此,在这里不考虑Mises屈服准则的预测结果。图8给出了不同屈服准则预测的值和值随RD加载角的偏差。
从图8中可以看出,在对值的预测方面,Hill48–、Barlat89、Yld2000–2d屈服准则的理论预测与试验值具有较好的一致性,对值的预测能力相差不大,而Hill48–的预测曲线表现出显著的差异;相反地,Hill48–对应力值的预测效果较好,Yld2000–2d屈服准则也表现出相同的效果,但是在Hill48–和Barlat89屈服准则中,观察到应力变化有显著的差异。为了进一步评估这几种屈服准则的适用性,需要对这些屈服准则的性能进行数值评价。因此,采用全局精度指数分析屈服准则对屈服轨迹形状、平面单轴应力和值分布的综合适用性[28],其数学表达式见式(16)。
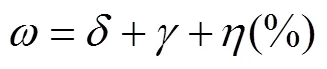
其中,
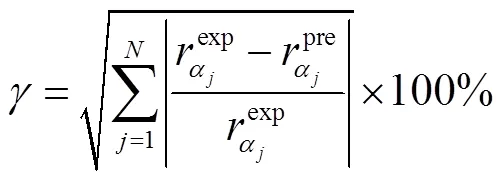
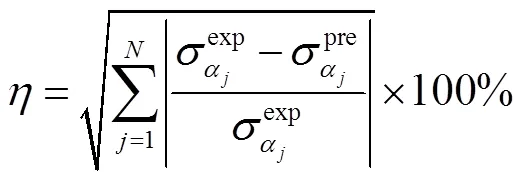
如图9所示,Hill48–屈服准则预测结果的误差值最大,达到42.46%;Hill48–和Barlat89屈服准则表现出相似的预测能力,误差结果相近,分别为21.10%和20.68%;Yld2000–2d屈服准则预测GH188在不同应力状态下的屈服行为的误差指数最小,仅有2.41%,远远小于其他3种屈服准则的预测误差,进一步表明Yld2000–2d屈服准则可以精确描述GH188高温合金板料在单向和多向应力状态下的屈服行为。

图8 不同屈服准则预测的屈服应力和r值

图9 评价不同屈服准则的精度指标
4 结论
通过单向拉伸和十字形双向拉伸试验,获得了钴基高温合金GH188板材的屈服轨迹,并与4种屈服准则的理论预测结果进行了对比,得到以下主要结论。
1)基于单向拉伸试验和Ludwik本构模型进行等双拉有限元仿真,模拟结果表明,所设计的十字形试件符合中心测量区应力分布均匀且无切应力的要求,试件形状尺寸具有合理性和有效性。
2)GH188高温合金的试验屈服轨迹关于等双拉线具有非对称性,表现出显著的各向异性属性,无论是采用值还是应力值求解的Hill48屈服准则均表现出与各向同性的Mises屈服准则相似的性质,不能描述具有各向异性的GH188试验屈服轨迹。
3)Hill48–和Barlat89屈服准则表现出相似的预测能力,Yld2000–2d屈服准则对GH188高温合金板材的屈服轨迹、单轴加载条件下的值和应力值都具有较高的预测精度,全局预测误差仅有2.41%,能够准确描述GH188板材在单向和多向应力状态下的屈服行为。
[1] LIU Da-hai, CHEN Jing-dong, CHAI Hao-rui, et al. Study of Meta-Dynamic Recrystallization Behavior of GH5188 Superalloy[J]. Journal of Materials Research and Technology, 2021, 15: 1179-1189.
[2] LIU Da-hai, CHAI Hao-rui, YANG Liang, et al. Study on the Dynamic Recrystallization Mechanisms of GH5188 Superalloy during Hot Compression Deformation[J]. Journal of Alloys and Compounds, 2022, 895: 162565.
[3] JAHED H, VARVANI-FARAHANI A, NOBAN M, et al. An Energy-Based Fatigue Life Assessment Model for Various Metallic Materials under Proportional and Non-Proportional Loading Conditions[J]. International Journal of Fatigue, 2007, 29(4): 647-655.
[4] LISSENDEN C J, COLAIUTA J F, LERCH B A. Hardening Behavior of Three Metallic Alloys under Combined Stresses at Elevated Temperature[J]. Acta Mechanica, 2004, 169(1): 53-77.
[5] CHABOCHE J L, GAUBERT A, KANOUTÉ P, et al. Viscoplastic Constitutive Equations of Combustion Chamber Materials Including Cyclic Hardening and Dynamic Strain Aging[J]. International Journal of Plasticity, 2013, 46: 1-22.
[6] REN Xin-yu, LI Wen-wen, JING Yong-juan, et al. Dissimilar Brazing of NbSS/Nb5Si3Composite to GH5188 Superalloy Using Ni-Based Filler Alloys[J]. Welding in the World, 2021, 65(9): 1767-1775.
[7] OUYANG Ling-xiao, LUO Rui, GUI Yun-wei, et al. Hot Deformation Characteristics and Dynamic Recrystallization Mechanisms of a Co-Ni-Based Superalloy[J]. Materials Science and Engineering: A, 2020, 788: 139638.
[8] XIAO Rui, LI Xiao-xing, LANG Li-hui, et al. Biaxial Tensile Testing of Cruciform Slim Superalloy at Elevated Temperatures[J]. Materials & Design, 2016, 94: 286-294.
[9] BANABIC D, BARLAT F, CAZACU O, et al. Advances in Anisotropy of Plastic Behaviour and Formability of Sheet Metals[J]. International Journal of Material Forming, 2020, 13(5): 749-787.
[10] 万敏, 程诚, 孟宝, 等. 金属板材屈服行为与塑性失稳力学模型在微尺度下的应用[J]. 精密成形工程, 2019, 11(3): 1-13.
WAN Min, CHENG Cheng, MENG Bao, et al. Mechanical Model for Yielding Behaviour and Plastic Instability of Sheet Metals and Its Application at Microscale[J]. Journal of Netshape Forming Engineering, 2019, 11(3): 1-13.
[11] 陈雷, 温卫东, 崔海涛. 双向应力状态下IC10高温合金的屈服行为研究[J]. 航空学报, 2012, 33(1): 77-84.
CHEN Lei, WEN Wei-dong, CUI Hai-tao. Measurement and Analysis of Yield Locus of Superalloy IC10 under Biaxial Tension[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(1): 77-84.
[12] KULAWINSKI D, ACKERMANN S, SEUPEL A, et al. Deformation and Strain Hardening Behavior of Powder Metallurgical TRIP Steel under Quasi-Static Biaxial-Planar Loading[J]. Materials Science and Engineering: A, 2015, 642: 317-329.
[13] LEOTOING L, GUINES D. Investigations of the Effect of Strain Path Changes on Forming Limit Curves Using an In-Plane Biaxial Tensile Test[J]. International Journal of Mechanical Sciences, 2015, 99: 21-28.
[14] 吴向东, 万敏, 周贤宾, 等. BH220钢板屈服轨迹的双向拉伸实验研究[J]. 塑性工程学报, 2004, 11(1): 39-42.
WU Xiang-dong, WAN Min, ZHOU Xian-bin, et al. Biaxial Tensile Experimental Study on the Yield Loci of Steel Sheet BH220[J]. Journal of Plasticity Engineering, 2004, 11(1): 39-42.
[15] 熊晶洲, 万敏, 孟宝, 等. 基于多轴同步控制的微尺度双向加载实验系统[J]. 北京航空航天大学学报, 2019, 45(1): 174-182.
XIONG Jing-zhou, WAN Min, MENG Bao, et al. Micro-Scaled Biaxial Loading Test System Based on Multi-Axis Synchronous Control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(1): 174-182.
[16] SHI Jie-jie, MENG Bao, CHENG Cheng, et al. Size Effect on the Subsequent Yield and Hardening Behavior of Metal Foil[J]. International Journal of Mechanical Sciences, 2020, 180: 105686.
[17] ZHENG Li-huang, CHENG Cheng, WAN Min, et al. Experimental Characterization and Theoretical Modeling of Size-Dependent Distortional Hardening Behavior of Ultrathin Metal Sheets under Multi-Axial Loading[J]. European Journal of Mechanics - A/Solids, 2022, 92: 104461.
[18] ZHENG Li-huang, WANG Kun, JIANG Yuan-yuan, et al. A New Ductile Failure Criterion for Micro/Meso Scale Forming Limit Prediction of Metal Foils Considering Size Effect and Free Surface Roughening[J]. International Journal of Plasticity, 2022, 157: 103406.
[19] CAI Z Y, MENG B, WAN M, et al. A Modified Yield Function for Modeling of the Evolving Yielding Behavior and Micro-Mechanism in Biaxial Deformation of Sheet Metals[J]. International Journal of Plasticity, 2020, 129: 102707.
[20] 江培成, 郎利辉, 邱超斌, 等. 拉伸比对2A16铝合金板材双向拉伸性能的影响[J]. 塑性工程学报, 2022, 29(1): 126-132.
JIANG Pei-cheng, LANG Li-hui, QIU Chao-bin, et al. Effect of Tensile Ratios on Biaxial Tensile Properties of 2A16 Aluminum Alloy Sheet[J]. Journal of Plasticity Engineering, 2022, 29(1): 126-132.
[21] KOTKUNDE N, BADRISH A, MORCHHALE A, et al. Warm Deep Drawing Behavior of Inconel 625 Alloy Using Constitutive Modelling and Anisotropic Yield Criteria[J]. International Journal of Material Forming, 2020, 13(3): 355-369.
[22] IFTIKHAR C M A, KHAN A S. The Evolution of Yield Loci with Finite Plastic Deformation along Proportional and Non-Proportional Loading Paths in an Annealed Extruded AZ31 Magnesium Alloy[J]. International Journal of Plasticity, 2021, 143: 103007.
[23] HU Qi, YOON J W, MANOPULO N, et al. A Coupled Yield Criterion for Anisotropic Hardening with Analytical Description under Associated Flow Rule: Modeling and Validation[J]. International Journal of Plasticity, 2021, 136: 102882.
[24] 金属材料拉伸试验第1部分:室温试验方法: GB/T 228.1—2010[S]. 北京: 中国标准出版社, 2011.
Metallic Materials - Tensile Testing - Part 1: Method of Test at Room Temperature: GB/T 228.1-2010[S]. Beijing: Standards Press of China, 2011.
[25] MERKLEIN M, BIASUTTI M. Development of a Biaxial Tensile Machine for Characterization of Sheet Metals[J]. Journal of Materials Processing Technology, 2013, 213(6): 939-946.
[26] Metallic Materials - Sheet and Strip - Biaxial Tensile Testing Method using a Cruciform Test Piece: ISO 16842[S]. ISO, 2014.
[27] 张飞飞, 陈劼实, 陈军, 等. 各向异性屈服准则的发展及实验验证综述[J]. 力学进展, 2012, 42(1): 68-80.
ZHANG Fei-fei, CHEN Jie-shi, CHEN Jun, et al. Review on Development and Experimental Validation for Anisotropic Yield Criterions[J]. Advances in Mechanics, 2012, 42(1): 68-80.
[28] MAHALLE G, MORCHHALE A, KOTKUNDE N, et al. Forming and Fracture Limits of IN718 Alloy at Elevated Temperatures: Experimental and Theoretical Investigation[J]. Journal of Manufacturing Processes, 2020, 56: 482-499.
Yield Behavior of Cobalt-based Superalloy GH188 Sheet Metal
MEN Ming-liang1, MENG Bao1, ZHU Yu2, SHI Pei-jue3, LIU Hong-mei3
(1. School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China; 2. Aero Engine Academy of China, Beijing 101304, China; 3. AECC Aviation Power Co., Ltd., Xi’an 710021, China)
The work aims to study the yield behavior of cobalt-based superalloy GH188 sheet metal under different stress conditions and to determine the applicable yield criterion, so as to provide scientific guidance for engineering applications. The basic mechanical property parameters were obtained by uniaxial tension tests in different directions. With rolling direction as the reference direction, the parameters of Ludwik constitutive model were calibrated with its real stress-strain curve. A cruciform specimen was designed according to the international standard. Finite element simulation of equi-biaxial tension was carried out by ABAQUS. Then the biaxial tensile test of GH188 superalloy sheet metal under different load ratios were carried out based on the designed specimen, and the yield point was obtained. Combined with the above data, the yield locus,-values and stress values were predicted with different yield criteria including Mises, Hill48, Barlat89 and Yld2000-2d. In the process of biaxial tension, the stress distribution in the center of the cross specimen was uniform and there was no shear stress, which indicated that the design of the specimen was reasonable and effective. The four yield criteria had little difference in the average prediction error of the experimental yield locus, which was (2±0.5)%. However, Hill48-had the largest prediction error in global, and Hill48-and Barlat89 yield criteria showed similar prediction ability with an error of about 20%. The Yld2000-2d yield criterion had the greatest prediction accuracy. Its global error was only 2.41%, which was far less than that of the other three yield criteria. Cobalt-based superalloy GH188 plate has obvious anisotropy, and Yld2000-2d yield criterion can accurately describe the yield behavior of the material under complex stress state
superalloy; GH188; cruciform specimen; yield criterion; yield locus
10.3969/j.issn.1674-6457.2023.02.017
TG386
A
1674-6457(2023)02-0142-09
2022–09–08
2022-09-08
门明良(1995—),男,博士研究生,主要研究方向为复杂钣金件多工序塑性成形数值模拟及跨尺度建模。
MEN Ming-liang (1995-), Male, Doctoral candidate, Research focus: numerical simulation and cross-scale modeling of multi-pass plastic forming of complex sheet metal components.
孟宝(1985—),男,博士,副教授,主要研究方向为跨尺度构件高性能成形制造理论与技术。
MENG Bao (1985-), Male, Doctor, Associate professor, Research focus: the theory and technology of high performance forming for cross-scale components and advanced forming process.
门明良,孟宝,朱宇, 等. 钴基高温合金GH188板材的屈服行为研究[J]. 精密成形工程, 2023, 15(2): 142-150.
MEN Ming-liang, MENG Bao, ZHU Yu, et al. YieldBehavior of Cobalt-based Superalloy GH188 Sheet Metal[J]. Journal of Netshape Forming Engineering, 2023, 15(2): 142-150.

