基于相似原理的液压泵重量估算方法研究

刘晓超， 王振宇， 邱钟毅， 齐鹏远， 吴 帅， 尚耀星， 焦宗夏

(1.北京航空航天大学 前沿科学技术创新研究院， 北京 100083；2.北京航空航天大学 自动化科学与电气工程学院，北京 100083)

引言

液压系统是飞机上最重要的机载系统之一，目前大多数的飞行器采用的液压系统是集中式的液压源，由飞机引擎驱动的液压泵产生高压流体，通过液压管路传递到执行机构完成驱动功能[1]。随着飞机特别是军用飞机不断向高速、高机动性和高能量效率方面发展，减轻飞机液压系统重量和缩小飞机液压系统体积是未来机载液压系统的发展趋势[2]。

但是，液压元件的重量估计由于样机数量限制，很难进行大量实物验证，需要通过其他间接的方法对液压元件进行准确的重量评估。国内学者关于液压系统和元件的重量评估与分析进行了大量工作：张文迁[3]利用遗传算法对液压支架的重量进行优化，最终使支架重量减小16.7%；范国浩[4]通过二维与三维软件的结合，对具有锻铸造结构的液压支架的重量进行估计，但是这种方法依赖于液压元件的三维模型，广泛应用于液压元件的重量估算存在一定的困难；谢立扬等[5]通过缸体弯曲极限力和能量转换的方法来求解液压打桩机锤头的重量，但是工况比较具体，对于不同研究对象适用性有待进一步研究。

自1848年法国科学院院士别尔泰[6]提出相似理论以来，主要应用于一些很难进行1∶1试验的研究当中，通过缩比模型与实物的相似关系，实现高精度的仿真分析[7-8]。龚军军等[9]以舰炮托架为研究对象，利用缩比模型与原型的模态参数对比分析，将模型仿真与实验结果的误差控制在10%以内。郭明珠等[10]基于相似理论分析，以量纲分析法为主，确定了振动台各物理量的相似比，为试验提供相似依据。同时，相似原理还广泛应用于液压系统与电气传动的相似类比[11-14]，提出液阻、液感、液容等概念，建立全新的液压系统模型，有利于对液压系统进行故障诊断。许耀铭[15]利用相似律，依据几何相似、运动相似等准则，探明液压泵、液压马达性能与相似律的关系，指导液压泵与马达的设计与改进。

对于机载系统液压重量估计方法， 同样可以采用相似原理进行分析。本研究提出一种基于相似原理的液压泵重量估计方法，同时进行了试验验证，以液压泵pv值作为约束条件，将几何相似比换算为液压泵性能参数的相似比，能够快速的进行不同液压泵重量的准确估计。研究结果表明，基于相似原理的液压泵重量估计具有较高的适用性和准确性。

1 液压元件重量估计方法

1.1 相似原理介绍

相似是指研究模型的每个要素必须与参考模型的对应要素相似，对于同一个物理过程，若两个物理现象的各个物理量在各对应点上以及各对应瞬间的大小成比例，且各矢量的对应方向一致，则称这两个物理现象相似，图1所示为相似原理的示意图，通过确定相似比实现相似估计。

图1 相似原理示意图

1.2 相似原理工作流程

如图2所示，相似原理的运用需要依赖已知的性能参数，选择合适的几何参数，通过真实物理模型建立性能参数相似比和几何参数相似比的数学联系，从而得到研究目标的相似比，最后根据大数据样本，得到最终的研究目标[16-17]。

图2 相似原理的工作流程图

对于给定特征参数的相似比可以表达为：

a*=a/aref

(1)

式中，a*—— 研究模型的特征参数值相似比

a—— 研究模型的特征参数值

aref—— 参考模型的特征参数值

根据式(1)所述原理，长方体部件的体积相似比和重量相似比可以直接通过相似比得到, 对于任意一个长方体部件体积相似比为：

(2)

式中，V*—— 长方体部件体积相似比

V—— 研究长方形部件体积

Vref—— 参考长方体部件体积

x—— 研究长方体部件的长

y—— 研究长方体部件的宽

z—— 研究长方体部件的高

xref—— 参考长方体部件的长

yref—— 参考长方体部件的宽

zref—— 参考长方体部件的高

x*—— 长方体部件的长度相似比

y*—— 长方体部件的宽度相似比

z*—— 长方体部件的高度相似比

同样，可以得到此长方体部件的重量相似比为：

(3)

式中，M*—— 长方体部件重量相似比

M—— 研究长方体部件重量

Mref—— 参考长方体部件重量

ρ—— 长方体部件材料密度

相似原理可以用来估算部件的其他特征，比如温度和能耗等特性。液压元件的重量估算也可以采用相似原理进行，对于相似原理估算液压泵的重量而言，需要2个假设：

假设1：研究对象和参考对象使用的材料相同，与材料特性相关的参数相似比都为1；

假设2：相似原理计算液压部件重量必须在相同的压力体制条件下进行，因为不同压力体制下对于部件厚度和强度要求均不同，会导致相似估算公式不同。

根据相似原理的假设条件，研究对象是由参考对象的物理模型在各个方向等比例缩放形成的，在相同的压力体制下，液压泵几何尺寸和液压泵重量有着一一对应的关系。如果选取液压泵柱塞绕缸体轴心的旋转半径为几何参数相似比，如图3所示，根据相似原理可以得到液压泵的体积和重量相似比为：

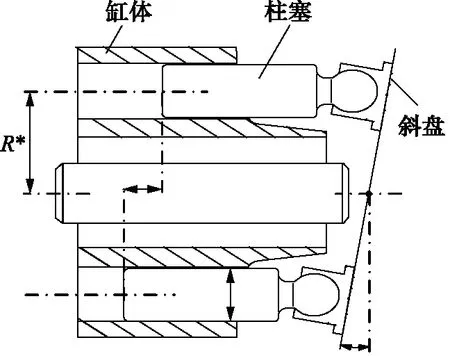
图3 液压泵几何尺寸

M*=V*=(R*)3

(4)

式中,R*为液压泵柱塞绕缸体轴心的旋转半径的相似比。

2 液压泵重量估计

2.1 相似参数确定

一般来说，很难得到任意一个液压泵柱塞绕缸体轴心的旋转半径R，所以需要寻找合适的性能参数来代替几何参数，通过物理模型建立性能参数相似比和重量相似比的数学联系来进行重量估计。液压系统体系对每一类部件都有确切的性能参数，这些参数基本就决定了部件的制造重量，比如液压泵性能参数就是输出功率P，不同的输出功率就对应不同的重量[18-19]。

液压泵的输出功率在液压系统设计中是可以得知的，在相同的压力体制条件下，不同的输出功率就对应不同的重量，所以选取液压泵功率作为性能参数，建立液压泵功率相似比和液压泵重量相似比的关系式，最终实现重量估计。

首先根据功率相似比的表达式：

P*=p*D*ω*

(5)

式中P*—— 液压泵功率相似比

p*—— 系统压力相似比

D*—— 液压泵排量相似比

ω*—— 液压泵转速相似比

根据假设条件，液压部件估算重量必须在相同的压力体制下进行，因此取p*=1，于是得到液压泵功率相似比最终表达式：

P*=D*ω*

(6)

液压泵排量实际上是液压泵旋转一周排油的体积，根据相似原理可以得到D*=(R*)3，因此根据物理模型得到转速性能参数相似比和几何参数相似比的数学关系，就可得到性能参数相似比和重量相似比的数学关系。

轴向柱塞泵是通过主轴带动缸体旋转实现吸油和排油，假设液压泵的转速与泵内部摩擦密切相关，即与液压泵摩擦副的pv值密切相关[20]，p代表密封流体压力(MPa)，v代表密封端面的平均滑移速度(m/s)，pv值的单位为MPa·m/s。

由于机械密封的密封面磨损率与pv值成正比，因此pv值可以用来反映摩擦副的工作寿命以及摩擦副材料组合的工作能力，同时机械密封工作时摩擦产生的热量与pv值成正比，因此pv值也是决定摩擦热的一个重要指标，应保证机械密封的工作pv值小于允许pv值[20-21]。假设液压泵采用相同的摩擦材料，所以p*v*=1，其中，p*代表系统压力相似比，根据假设条件，p*=1，同理可以得到v*=1，根据液压泵物理模型，可以得到密封端面平均滑移速度相似比v*的表达式：

v*=ω*R*=1

(7)

通过假设机械密封的工作pv值小于允许pv值，根据式(5)～式(8)，得到转速相似比和几何参数相似比的数学关系表达式：

ω*=(R*)-1=(D*)-1/3

(9)

最终，得到性能参数功率相似比和重量相似比的数学关系表达式为：

P*=D*ω*=(R*)3(R*)-1=(R*)2=(M*)2/3

(10)

M*=(P*)3/2

(11)

或者液压泵流量相似比和重量相似比的数学关系表达式可写为：

Q*=D*ω*=M*2/3

(12)

M*=(Q*)3/2

(13)

式中,Q*为液压泵流量相似比。

满足性能参数完全相似的液压泵或者液压马达，性能参数之间的关系均服从同一关系方程[16]。综上，若使用相似原理方法估算液压泵的重量，在相同压力体制条件下，只要知道液压泵的输出功率或者输出流量，就可以比较准确的估算出液压泵的重量[22]。

2.2 相似重量估计验证

为了验证假设的正确性，结合大数据验证转速相似比和几何参数相似比的数学关系，通过搜集到的PARKER公司和EATON公司的21 MPa液压泵数据(如表1、表2所示)进行验证。

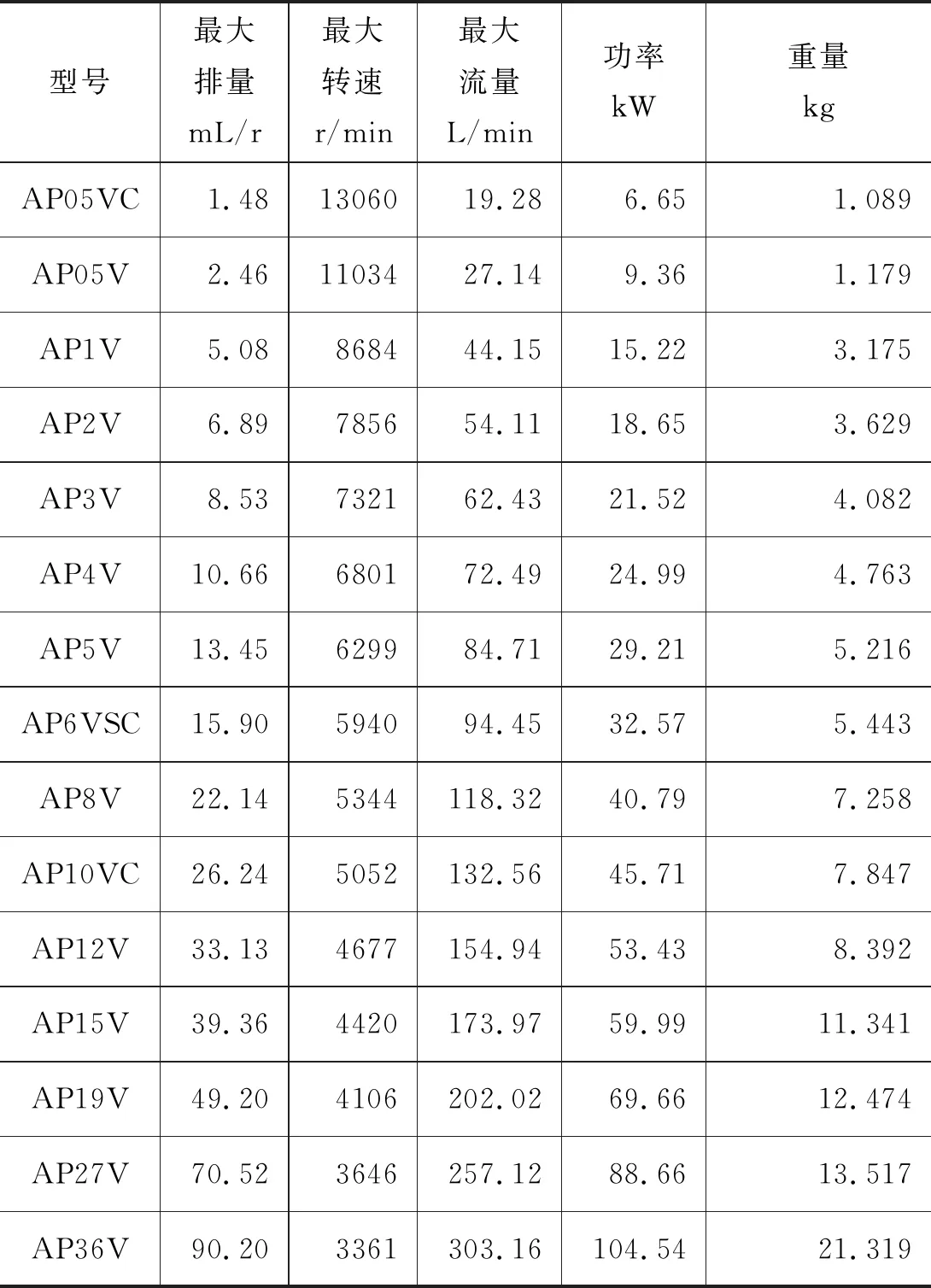
表1 PARKER液压泵相关数据

表2 EATON液压泵相关数据

如图4所示，分别是ω-D关系曲线和ω-D-1/3关系曲线，可知ω-D关系曲线呈现不规律关系，然而ω-D-1/3关系曲线呈现非常精确的线性关系，如图5所示，说明根据pv值假设得到转速相似比和几何参数相似比是可行的。

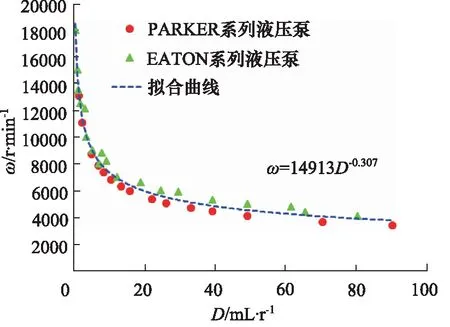
图4 液压泵ω-D大数据验证曲线

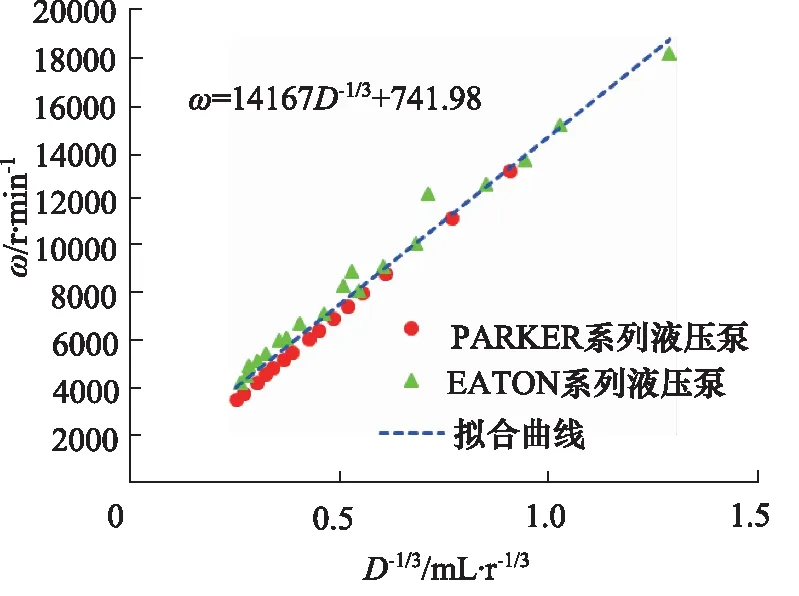
图5 液压泵ω-D-1/3大数据验证曲线

为了进行21 MPa压力等级条件下的液压泵重量估算，利用搜集到的PARKER公司和EATON公司的21 MPa的液压泵数据进行分析，如图6所示，可以看到，液压泵的重量跟液压泵的流量的三次方的开方呈现精确的线性关系。如图7所示，液压泵的重量跟液压泵的功率3次方的开方也呈现精确的线性关系，因此根据液压泵的流量或者液压泵的功率遍可以估算出液压泵的重量。

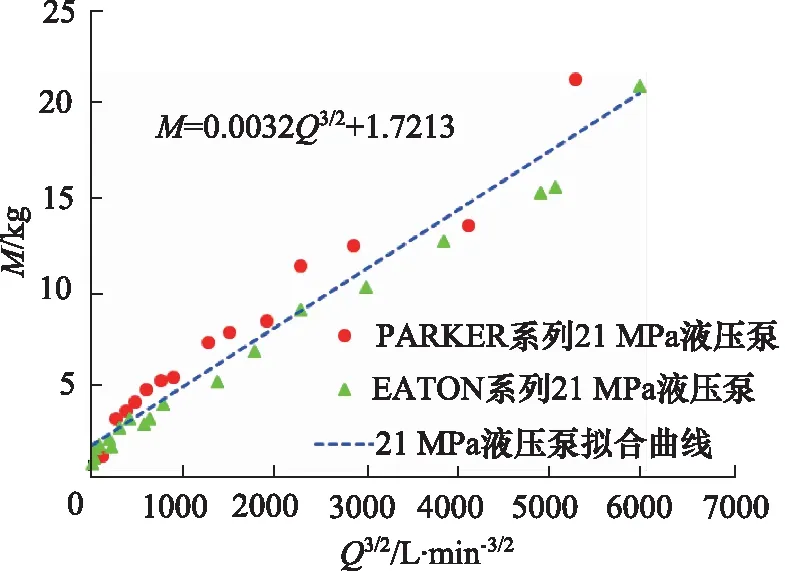
图6 21 MPa液压泵M-Q3/2大数据验证曲线

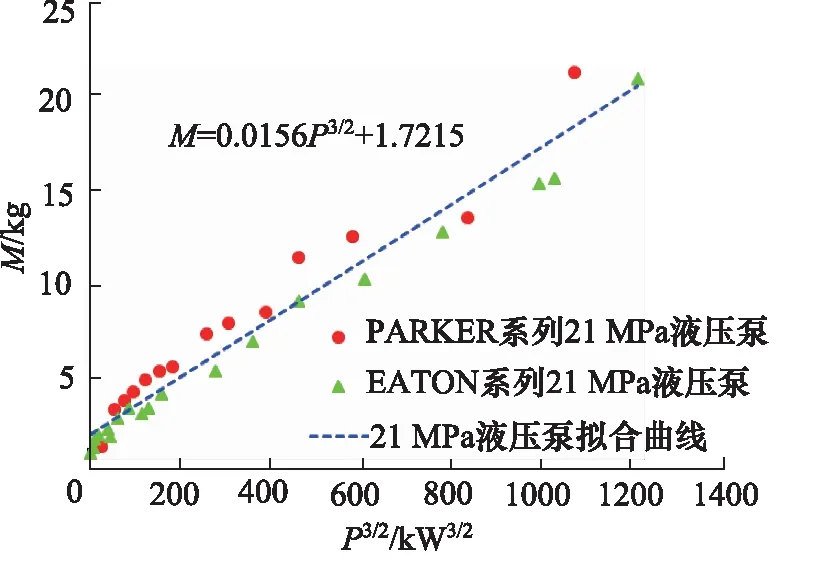
图7 21 MP液压泵M-P3/2大数据验证曲线

通过M-Q3/2曲线进行数据拟合得出，液压泵的重量跟液压泵的流量关系表达式：

M=0.0032×Q3/2+1.7213

(14)

通过M-P3/2曲线进行数据拟合得出，液压泵的重量跟液压泵的功率关系表达式：

M=0.0156×P3/2+1.7215

(15)

同理，为了进行35 MPa压力等级条件下的液压泵重量估算，利用搜集到的MBD公司和PARKER公司的35 MPa的液压泵数据进行分析，如表3所示。

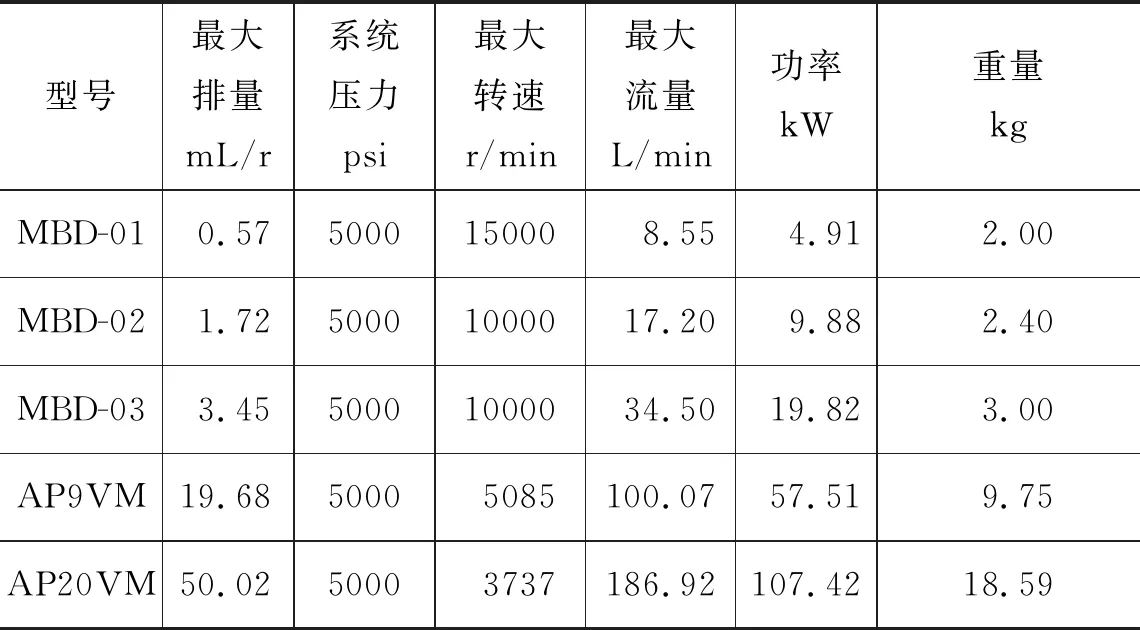
表3 35 MPa液压泵相关数据

如图8所示，通过M-Q3/2曲线可以得出，液压泵的重量跟液压泵的流量关系表达式：

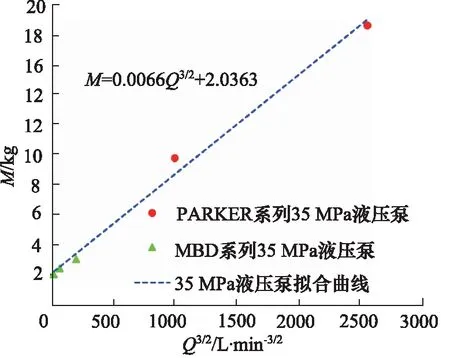
图8 35 MPa液压泵M-Q3/2大数据验证曲线

M=0.0066×Q3/2+2.0363

(16)

如图9所示，通过M-P3/2曲线可以得出，液压泵的重量跟液压泵的功率关系表达式：

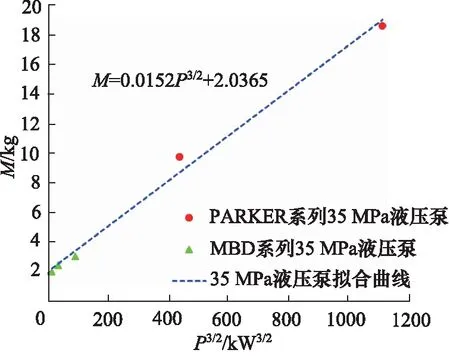
图9 35 MPa液压泵M-P3/2大数据验证曲线

M=0.0152×P3/2+2.0365

(17)

3 液压泵重量估计验证

根据上述重量估计方法对压力为35 MPa、流量为30 L/min的液压泵进行重量估计，可以估算出液压泵重量为3.120 kg。通过单独测量相应参数液压泵的重量，对相似原理估算的样机重量结果进行校核与验证。如图10所示，液压泵的测量重量为2.970 kg，与重量估计误差为4.8%，根据相似原理进行液压元件重量估算的方法具有较高的估算精度。

图10 液压泵称重结果

同时基于相似原理同样能够对液压马达进行重量估计，图11所示为液压马达称重结果，重量估计结果与实际重量1.611 kg非常接近，估计结果具有较高的精度。

图11 液压马达称重结果

4 结论

(1) 通过相似原理进行液压泵的重量估计是一种可行的方法；

(2) 通过将液压泵结构参数相似比转换为性能参数相似比进行液压泵重量的估计，可以更方便的进行液压泵的重量估计；

(3) 采用液压泵的pv值作为相似原理估算的约束条件，能够得到较为准确的估计结果，估计误差为4.8%。

针对系列比较完善的液压泵，如果结合大数据插值拟合方法进行综合分析，将得到更为理想的结果。但是对于正处于设计阶段、尚未形成系列的特种液压泵，没有足够的数据支撑，相似原理为液压泵重量估计提供了一种新的方法。