井下原位测量装置推靠机构力学分析及仿真
白保鑫,吴 伟,张建伟,王金超
(西安石油大学 机械工程学院,西安 710065)
0 引言
“井下原位测量装置”作为同时满足井壁取芯、岩心测量和流体测量条件的新型地层信息勘测方法逐渐被国内外各大能源服务公司采用并研究[1]。目前,关于井下原位测量装置推靠机构的运动学及动力学分析方面的研究较少,缺乏详细的理论分析模型,因而无法准确描述井下测量装置推靠系统的真实的运动状态和运动规律。文献[2]利用复数矢量法进行新型分动式六臂井径测井仪推靠系统运动学及动力学分析,得到了该测井仪推靠机构各杆件的位置方程、速度方程及加速度方程;文献[3]用矩阵解析法对微电阻率扫描测井仪极板推靠机构运动学进行分析,从而得到该测井仪推靠机构各杆件运动参数,真实反映推靠机构的实际运动状况。
推靠机构运动性能的好坏直接影响取芯效率及测井数据的准确性[4]。本文就井下原位测量装置推靠机构运动学及动力学进行研究,运用复数矢量法得到井下原位测量装置推靠机构各杆件的位置方程、速度方程及加速度方程,并对各杆件进行动态静力学分析得到了动态静力学方程;通过MATLAB建立推靠机构数学分析模型,得出该模型运动学特性理论变化曲线;运用Adams对井下原位测量装置推靠机构进行虚拟样机建模和运动仿真,进一步分析了其运动规律,有助于在地层信息勘探中实现输出运动的最大精度,为后续推靠机构动力学分析及结构参数优化提供了理论依据[5]。
1 井下原位测量装置推靠机构物理模型建立
本文设计的井下原位测量装置三维图如图1所示,推靠范围为140~257 mm,提供的推靠力为2×100 kg。推靠机构结构如图2所示,由推靠臂、推靠板、推靠辅助臂、推靠液压缸组成。推靠模块分别由液压缸6、13提供动力,辅助臂1、推靠板2、推靠臂3组成曲柄连杆机构,同样推靠臂7、推靠板8、辅助臂9也组成曲柄连杆机构。当推靠液压缸6、13的液压活塞杆推出时,通过推靠臂3、7分别作用在曲柄连杆机构上,使得推靠板2、8从仪器上打开并将井壁取芯测量装置推靠在井段侧壁上。当推靠液压缸不断提供压力作用在推靠板上时,仪器取芯口一侧得以牢靠紧密贴合井壁为后续取芯测量工作奠定工作基础。当推靠液压缸活塞杆回退时就可以把推靠板收回到仪器上,并能够和仪器外壳完全贴合。由于该机构采用两个液压缸分别对两个推靠板提供动力,故在环境复杂的裸井环境中,通过调节两个液压缸的油量供给以使各推靠板能够贴合不同的井段侧壁,从而使整个仪器能够保持合适的姿态进行作业。

图1 井下原位测量装置3D结构示意图

图2 井下原位测量装置结构示意图
2 推靠机构工作过程力学分析
当仪器下放至指定深度时,推靠活塞伸出,使仪器紧贴在井壁,用以进行钻进取芯及后续工作。将推靠活塞合理设置在钻头两侧(仪器上端与下端各一个),双点推靠使仪器钻头钻进面紧贴井壁进行钻进取芯、探头测试,整个钻进测试过程中仪器推靠牢固,仪器不偏移不偏转。在此机构中,构件个数为4,移动副个数为1,滚滑副个数为4。并且,机构中存在1个虚约束,故机构的自由度数为1,即推靠机构具有确定运动[6]。
2.1 推靠机构工作过程运动学分析
如图3所示,已知推靠液压推杆初始位置为A,以V1匀速轴向向下运动,且杆件OA与OB的夹角为恒定角θ3。取两铰链固定点为X轴,Y轴过O点,设AA′、AO、OA′、OB′对应 杆件长度分别 为lk、l3、l3′、l4′,且AO、OB、A′O、OB′分别对应的方位角θ(以X轴的正向逆时针度量)为θOA′、0、θOA′、2π-θ1,对应的矢量为l3、l4、

图3 推靠机构工作状态运动简图
2.1.1 推靠机构工作过程中各构件位置分析
以复数形式表示为:
式中:θOA=π+θ3,θOA′=θ3-θ1,l3′、θ1为未知量。
按欧拉公式展开得:
化简,且令等式两边实部虚部相等可解得:
可知,推靠杆A点空间位置为:
按封闭矢量图形A′OB′A′分析构件4(推靠臂)B点位置。矢量三角形A′OB′是由矢量l3、l4′、lA′B′所构成,建立封闭矢量方程如下:
以复数形式表示为:
式中:θ2和lA′B′为未知量。
按欧拉公式展开,令等式两边实部虚部相等得:
等式两边同时平方,解得:
可知,B点的空间位置坐标为:
由构件5(推靠板)位于构件4(推靠臂)与构件6(辅助臂)中心线上,故构件5的平面位置坐标为:
2.1.2 推靠机构工作过程中各构件速度分析
在A点进行对杆件3进行速度分析,设A点的合运动vA,那么
故
杆件3与杆件4固定连接,以O点为铰链中心做圆周运动,即
以复数形式表示为:
将式(6)对时间求导数得:
上式为vB+vCB=vc的复数矢量表达式。将式的实部与虚部分离,有
联解上式可求得两个速度v5、ω6,即
且v5为过连杆质心作与原点O连线的垂线上。
2.1.3 推靠机构工作过程中各构件加速度分析
将式(16)对时间t求导,可得
将式(20)的实部与虚部分离,有
联解上式可求得加速度ε5、ε6,即
即
将式(24)对时间t分别求一次和二次导数,并经变换整理可得v和εE的矢量表达式[9]。
2.2 推靠机构工作过程动力学分析
动力学分析符号说明:F为液压缸给液压推杆的作用力;T为井壁对推靠板的作用力;mi、Ji分别为构件i的质量和对其质心的转动惯量;Fijx、Fijy分别为通过回转副第i个构件给第j个构件在x、y方向的约束反力;(LIJ)x、(LIJ)y分别为由点I到点J的矢量在x、y方向的分量;aSix、aSiy为第i个构件的质心Si的加速度在x、y方向的分量;εi第i个构件的角加速度;g为重力加速度[10]。运动学求解部分已经得到了各杆件的加速度,从而可求出各杆件所受的惯性力以及惯性力矩。根据支臂受力情况,分别以各构件为研究对象,建立动力学平衡方程。
(1)液压推杆2受力情况如图4所示。动力学平衡方程为:

图4 液压推杆2受力分析简图
(2)主力杆4受力情况如图5所示。动力学平衡方程为:
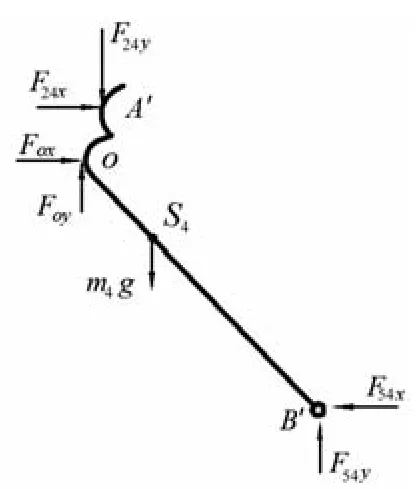
图5 主力杆4受力分析简图
(3)推靠杆5受力情况如图6所示。动力学平衡方程为:
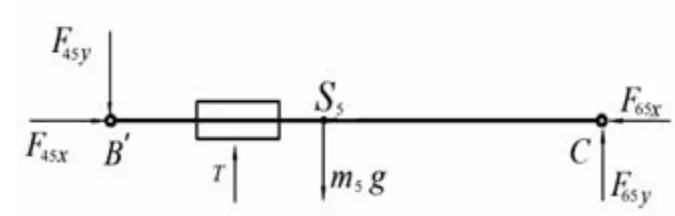
图6 推靠杆5受力分析简图
(4)辅助杆6受力情况如图7所示。动力学平衡方程为:

图7 辅助杆6受力分析简图
3 MATLAB建模
生成了用于推靠机构位置分析的MATLAB代码。MATLAB编程的目的是计算推靠机构给定最大推靠位置时主力杆与井下原位测量装置轴线夹角θ1的值。推靠机构分析的输入变量包括:推靠机构各杆件长度[11-12];主力杆角速度ω1。图8显示了各种系统配置中推靠杆5质心位置和主力杆转角θ1之间的关系,当θ1=29.3°时,推靠机构推靠杆推靠最大行程达到257 mm。
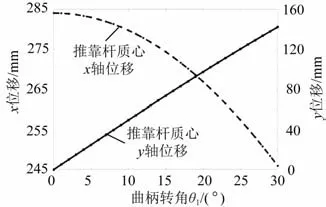
图8 推靠杆5质心位置和主力杆转角θ1之间的关系图
4 ADAMS运动学仿真分析与结果
ADAMS运动学仿真的目的有:
(1)通过脚本控制的各模块运动,观察是否有构件在作业过程中产生运动干涉;
(2)通过分析ADAMS软件后处理的仿真结果来判断原有模型设计仿真是否能够满足设计要求与技术指标[13]。
在Solidworks中建立井下原位测量装置的三维简化模型,并只保留井下原位测量装置推靠机构,将建立的三维模型另存为Parasolid(*.x_t)格式输出,然后导入Adams环境中如图9所示,工作过程中,推靠机构2个极板的运动状态是相同的,所以通过简化模型,运用Adams中的Adams/view模块只对该推靠机构中的一组机构进行结构参数化设计[14],并在各关键点处添加约束如表1所示设置推靠机构的运动参数,为1 d在运动副的Function(time)栏设置曲柄l1旋转位移为1d*time。

图9 推靠机构仿真模型图

表1 各杆件连接约束表
在ADAMS/View中创建完推靠机构后,下一步就是对该模型进行仿真,并得到输出结果。推靠臂与井下原位测量装置轴线最大夹角为29.3°,主力杆4不能完全360度旋转,只能振荡,所以在ADAMS中以0-29.3 s为间隔,仿真步数设置为1 500进行仿真,并通过后处理Postprocessor功能对虚拟样机仿真运动结果进行分析分析[15]。
由图10(a)可知主力杆4在液压推杆2的作用下,由静止状态开始受力,推靠杆5加速度有突变,此情况下可能会引起整个仪器的振动。推靠杆质心的线速度也会在一段时间内变化然后变成常数[16]。图10(b)表明推靠杆5质心位置沿着x轴方向移动42 mm,图10(c)表明推靠杆5质心位置沿着y轴方向移动120 mm,最大测量井径达到260 mm。将ADAMS仿真结果与前面matlab理论仿真结果(图8)对比分析,可发现理论仿真的结果基本符合ADAMS仿真结果,能够正确反映出实际的运动轨迹与趋势,满足设计要求。

图10 推靠杆5质心运动位移、速度、加速度变化曲线
由图11可知,液压推杆2运行初期由于各铰接点间存在一定的间隙出现加速度突变,在推靠杆达到最大推靠位置时,沿x轴方向平移了34.5 mm,由此液压推杆行程得以确定。
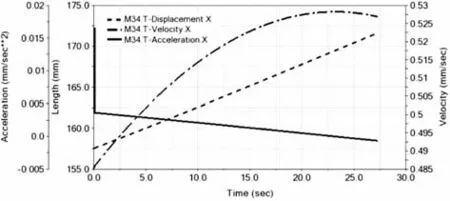
图11 液压推杆2行程图
5 结束语
(1)基于复数矢量法构造推靠系统运动机构参数方程,建立了井下原位测量装置推靠机构模型,为井下原位测量装置推靠机构系统的理论研究和生产制造提供了依据。
(2)通过对推靠系统数学模型的运动分析,研究推靠系统中液压推杆的运动行程以及机构中输出构件推靠杆的运动曲线,得到其推靠系统各杆件运动参数,真实反映推靠系统的实际运动状况。
(3)通过推靠系统运动学分析获取的运动学参数,为其结构参数优化设计提供参数支撑,以便进一步优化井下原位测量装置,提高设计效率。为后续的动力学分析以及推靠杆的摩擦、磨损分析也奠定了基础。

