直击统计图表的应用
高 诤
(山东省济南市章丘区第五中学)
无论是中考还是高考,统计图表都是命题的重点,这类问题不但能考查数据分析、数学建模和数学运算等素养,而且能体现“学以致用”的命题原则.本文分析在高考命题中,涉及统计图表应用的基本考点.
1 频率分布直方图
在中学数学的统计内容中,频率分布直方图应用较为广泛,在高考命题中出现的频率也比较高.它在选择题、填空题和解答题中都有可能出现,主要考查学生能利用频率分布直方图计算出有关样本估计总体的数据和统计特征值.
例1在实施“乡村振兴”的进程中,某地政府引领广大农户发展特色农业,种植优良品种柑橘.现在实验基地中种植了相同数量的A,B两种柑橘.为了比较A,B两个柑橘品种的优劣,在柑橘成熟后随机选取A,B两种柑橘各100 株,并根据株产量X(单位:kg)绘制了如图1所示的频率分布直方图(数据分组为[65,70),[70,75),[75,80),[80,85),[85,90),[90,95]).
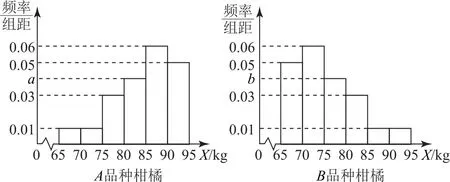
图1
(1)求a,b的值;
(2)将频率当做概率,在所有柑橘中随机抽取一株,求其株产量不低于80kg的概率;
(3)求两种柑橘株产量平均数的估计值(同一组数据中的平均数用该组区间的中点值代表),并从产量角度分析,哪个品种的柑橘更好? 说明理由.
(2)A品种柑橘株产量不低于80kg 的频率为(0.04+0.05+0.06)×5=0.75,B品种柑橘株产量不低于80kg 的频率为(0.03+0.01+0.01)×5=0.25,故200株柑橘中产量不低于80kg 的频率为,所以在所有柑橘中随机抽取一株,其株产量不低于80kg的概率为0.5.
(3)A品种柑橘株产量平均数的估计值为MA,且
设B品种柑橘株产量平均数的估计值为MB,且
A品种的柑橘更好,理由如下.
方法1A的平均产量大于B的平均产量.
方法2由频率分布直方图可知,A品种柑橘株产量在80kg及以上的占比为75%,B品种柑橘株产量在80kg及以上的占比为25%.
2 茎叶图
在高考中常要求考生通过茎叶图观察出平均数、众数、中位数、数据分布的对称性等,由于茎叶图保留了原始数据,还可计算平均数、方差、标准差.对茎叶图的考查以选择题为主.
例2从某中学甲、乙两班各随机抽取10名同学,测量他们的身高(单位:cm),所得数据用茎叶图表示如图2所示,由此可估计甲、乙两班同学的身高情况,则下列结论正确的是( ).
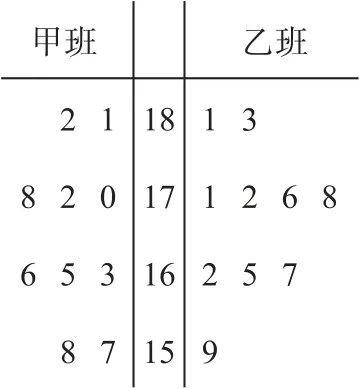
图2
A.甲、乙两班同学身高的极差不相等
B.甲班同学身高的平均值较大
C.甲班同学身高的中位数较大
D.甲班同学身高在175cm以上的人数较多
对于B,甲班同学身高的平均值为
乙班同学身高的平均值为
所以甲班同学身高的平均值较小,故B错误.
对于D,甲班同学身高在175cm 以上的有3人,乙班同学身高在175cm 以上的有4人,所以甲班同学身高在175cm 以上的人数较少,故D 错误.
综上,选A.
3 其他统计图表
高考中除了考查频率分布直方图和茎叶图的应用外,还常常考查条形图、扇形图、折线图、总体密度曲线、雷达图等其他统计图表.
例3某家保险公司的保险产品有以下五种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险;戊,重大疾病保险.各种保险按相关约定进行参保与理赔.该保险公司对五个险种的参保客户进行抽样调查,统计图(如图3、图4、图5),则以下说法正确的是( ).
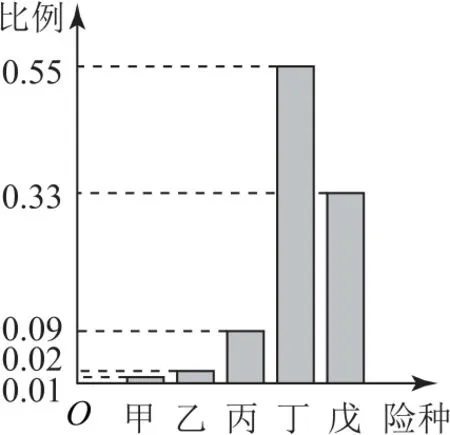
图3 参保险种比例
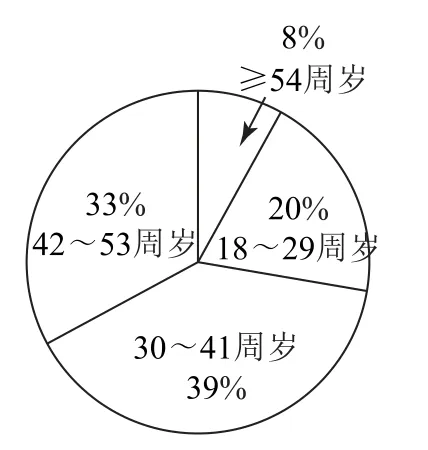
图4 参保人年龄分布
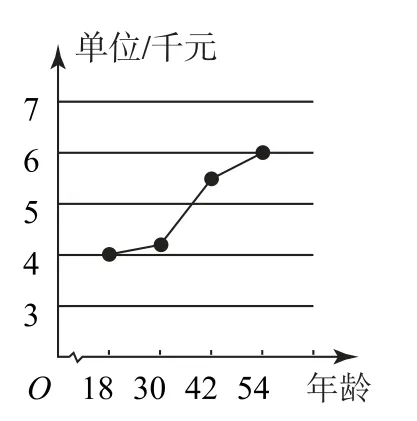
图5 不同年龄段人均参保费用
A.42~53周岁客户人数是不低于54周岁的客户人数的4倍多
B.不低于54周岁客户参保总费用最多
C.丁险种人均参保费用最低
D.戊险种参保人都是42~53周岁的客户
综上,选A.
高考对统计图表的考查难度不大,大多是基础题,主要考查考生的识图能力和利用统计图表解决实际问题的能力,所以复习此类问题只需领会统计图表的意义、把握基本知识、掌握基本方法,基于高考命题特点,建议大家“广积粮”,但不宜“深挖洞”.
(完)

