基于Dropout-LSTM模型的城市燃气日负荷预测

于铭多，郝学军

(北京建筑大学 环境与能源应用工程学院，北京 100044)

1 概述

城市燃气负荷预测指分析燃气负荷特性、预测未来一段时间内用气规律和特征[1]，其中日负荷预测可为燃气短时间内的使用情况提供一定理论依据，便于对燃气合理规划、调配。

从燃气负荷预测的研究进程来看，国内外燃气负荷预测研究方法主要分为2种：一是传统的数理方法，如回归分析法、时间序列法等；二是人工智能类方法，主要以机器学习和新兴的信号分析方法等理论为基础，包括支持向量机、人工神经网络等[2]。Gorucu[3]利用多元统计回归法对安卡拉的天然气用量进行了预测；Beyzanur等人[4]提出了一种结合遗传算法(GA)和自回归移动平均(ARIMA)方法的预测方法，对伊斯坦布尔的天然气消耗量进行预测；郭微等人[5]应用支持向量机方法预测了天然气负荷；Kizilaslan等人[6]通过对几种不同神经网络算法的比较，建立了适合伊斯坦布尔的天然气日负荷预测模型；何恒根等人[7]采用BP 神经网络模型进行燃气负荷预测，得到了较高的预测精度。

目前神经网络在燃气预测领域应用最为广泛，其中BP等传统神经网络无法识别出数据之间的关联性，因此提出了一种循环神经网络(RNN)，主要用于处理和预测序列数据。由于简单的RNN具有长期记忆能力不足等问题，有学者研发了一种新型循环神经网络——长短期记忆神经网络(Long Short-Term Memory,LSTM)，可以学习长期依赖信息。文献[8-9]选取LSTM、BP神经网络等模型进行预测分析，结果表明LSTM模型优于其他模型。

城市燃气日负荷是具有很强的周期性的序列数据，因受到外界各种因素影响，同时具有不确定性和随机性，一般预测方法不能很好模拟出日负荷的波动情况。为进一步提高预测精度，本文提出一种基于LSTM神经网络的燃气日负荷预测方法，并针对神经网络模型在训练过程中易陷入过拟合的现象，应用Dropout技术对LSTM 网络进行优化，使得构建的神经网络模型具有更强的泛化能力。由于不同时期的燃气日负荷特性不同，将历史数据分组并进行相关性分析，分别建立供暖期、过渡期及非供暖期3个Dropout-LSTM预测模型，并将模型应用于某市的日负荷预测进行验证，结果表明3个Dropout-LSTM模型均具有较好的预测效果，可应用于燃气日负荷预测。

2 燃气日负荷特性

以华北某城市2018年1月1日至2020年12月31日的燃气日负荷为例，分析城市燃气日负荷特点。该城市供暖期为11月15日至次年3月15日。城市燃气日负荷受自然条件和人为因素影响。其中自然条件一般包括温湿度、风力等级、天气情况、日期属性等，人为因素包括市民自行设定室内温度、调节供暖时间等。燃气负荷时间序列蕴含大量的负荷变化规律信息，依此可以有效预测未来燃气负荷[10]。燃气日负荷与日均温度随时间的变化曲线见图1。由图1可知，该城市燃气日负荷有较强的年周期规律性，且与温度有明显相关性，在供暖期尤为显著。另经分析发现，部分节假日(如清明节假期、劳动节假期等)日负荷并无差异，仅在春节假期和国庆节假期等重大节假日出现波动。图2展示了2018年不同星期类型(周一至周日)燃气日负荷变化趋势。供暖期燃气日负荷周峰谷差和不同星期类型燃气日负荷的波动都较为剧烈，但一周内不同星期类型的日负荷无显著差异，可见星期类型对日负荷没有较大影响。

图1 燃气日负荷与日均温度随时间的变化曲线

图2 2018年不同星期类型的燃气负荷变化趋势

3 预测模型构建

3.1 LSTM网络

LSTM单元结构中包括遗忘门ft、输入门it和输出门ot[11]。遗忘门决定了当前时刻的单元状态ct可以保留多少上一时刻单元状态的信息；输入门决定了单元状态ct可以接收多少网络的输入xt的信息；输出门通过激活函数Sigmoid控制当前输出，随后与tanh函数处理的单元状态相乘共同确定最终的输出ht。

图3 LSTM单元结构

3.2 Dropout技术

影响城镇燃气日负荷的因素较多，因此模型的参数较为复杂，且对于LSTM网络这种规模较大的神经网络来说，本文样本数据较少，训练样本不够充足，很容易产生过拟合现象。文献[12]提出了Dropout 正则化方法，能有效避免过拟合并改善模型性能，在神经网络中得到了广泛应用。为提高模型预测精度，解决过拟合问题，本文在LSTM网络基础上引入Dropout技术。

3.3 Dropout-LSTM燃气日负荷预测模型建立

本文基于Python软件Keras深度学习框架中的Sequential模型搭建两层Dropout-LSTM 网络模型。在模型训练中，使用Adam优化算法代替传统的随机梯度下降算法，Dropout神经元失活概率为0.2，更新器的学习率为0.01。

4 Dropout-LSTM模型的预测流程

① 提取数据：采集历史燃气日负荷及相关影响因素数据。

② 数据预处理：数据预处理的作用主要是防止异常数据波动而引起训练时间的增加，有效提高模型预测精度[13]。处理内容包括缺失值的插补、异常值的剔除与填补、数据的定量化以及归一化。

a.采集用气数据后未发现存在缺失值，经局部异常因子算法(Local Outlier Factor，LOF)筛选并剔除异常值后，经拉格朗日插值法进行填补，由此得到最终样本数据。

b.输入特征对预测模型的性能影响较大[14]，本文选择风力等级、天气类型、日平均温度、日最高温度、日最低温度、历史日负荷、星期类型和节假日类型这几种影响燃气日负荷的因素构成输入特征，其中风力等级、天气类型、星期类型、节假日类型为定性数据，需要进行量化处理。量化规则对于预测结果产生一定影响，研究发现，将影响因素的定性信息映射于[0，1]区间的中后段时，预测结果具有较好的准确性[15]，本文参考相关文献中量化规则并结合实际情况，对影响因素进行量化，量化数据见表1～4。采用Min-Max归一化方法将日平均温度、日最高温度、日最低温度和历史日负荷映射到[0,1]区间，公式为：

(1)

式中xg——日平均温度、日最高温度、日最低温度或历史日负荷归一化后的值

x——日平均温度、日最高温度、日最低温度或历史日负荷的实际值

xmin——日平均温度、日最高温度、日最低温度或历史日负荷实际数据中的最小值

xmax——日平均温度、日最高温度、日最低温度或历史日负荷实际数据中的最大值

表1 风力等级的量化数据

表2 天气类型的量化数据

表3 星期类型的量化数据

续表3

表4 节假日类型的量化数据

③ 相关性分析：应用SPSS统计软件对燃气日负荷与影响因素进行Pearson相关性分析，随后确定模型的输入特征。

④ 构建Dropout-LSTM模型：确定训练集和测试集。将训练集数据输入已构建好的Dropout-LSTM模型中进行训练。

⑤ 输出结果：将测试集数据输入Dropout-LSTM模型中进行测试，输出测试集的预测值，并将预测值与真实值进行比较，评估模型的性能及预测效果。本文选取燃气负荷预测中应用最广泛的平均绝对百分比误差来衡量真实值与预测值之间的偏差，平均绝对百分比误差计算公式为：

(2)

式中IMAPE——平均绝对百分比误差

n——样本的数量

yi,p——第i个样本的预测值

yi——第i个样本的真实值

平均绝对百分比误差越接近0，说明模型预测结果越准确。

5 Dropout-LSTM模型的预测

① 全年3个时期的划分

将全年分为供暖期(1月1日—3月15日、11月15日—12月31日)、过渡期(3月16日—4月15日、10月16日—11月14日)以及非供暖期(4月16日—10月15日)3个时期。不同时期的燃气日负荷特性有所差别，因此建立供暖期、过渡期和非供暖期3个Dropout-LSTM模型，并探究每一时期燃气日负荷与影响因素的相关性，确定对应模型的输入特征，分别对3个时期的燃气日负荷进行预测。

② 确定3个时期模型的输入特征

不同时期燃气日负荷与影响因素的Pearson相关性分析见表5。相关系数绝对值越接近1表示两个变量的相关性越强，越接近0表示相关性越弱。当相关系数绝对值在区间[0.4,1.0]表示呈强相关性，在区间[0.15,0.40)表示呈弱相关性，在区间[0,0.15)表示无相关性。3个时期的燃气日负荷都与日均温度、日最高温度、日最低温度、前一天负荷、前二天负荷、前三天负荷呈强相关性。另外，供暖期日负荷与节假日类型和风力等级呈弱相关性，与天气类型和星期类型无相关性；过渡期日负荷与风力等级呈弱相关性，与天气类型、星期类型和节假日类型无相关性；非供暖期日负荷与天气类型和风力等级呈弱相关性，与星期类型和节假日类型无相关性。

为保证预测的准确性，考虑更多输入特征，本文选取与燃气日负荷呈强、弱相关性的影响因素作为不同时期模型的输入特征，见表6。

表5 不同时期燃气日负荷与影响因素的Pearson相关性分析

续表5

③ 确定3个时期模型的训练集和测试集

分别将采集到的供暖期、过渡期和非供暖期数据划分为训练集和测试集，具体划分情况见表6。以供暖期模型为例，将2018年1月4日—3月15日、2018年11月15日—12月31日、2019年1月1日—3月15日、2019年11月15日—12月31日、2020年1月1日—3月15日、2020年11月15日—12月11日每日的8个特征(日均温度，日最高温度，日最低温度，节假日类型，风力等级，其前一、二、三天负荷)和日负荷组成1个样本，将这些样本作为训练集用于模型训练。将训练集内第N日的日均温度、日最高温度、日最低温度、节假日类型、风力等级和第N-1日负荷、第N-2日负荷、第N-3日负荷作为输入，模型输出为第N日的日负荷。将2020年12月12日—31日的样本作为测试集。

④ 预测效果对比分析

为验证Dropout-LSTM 模型具有较高的预测能

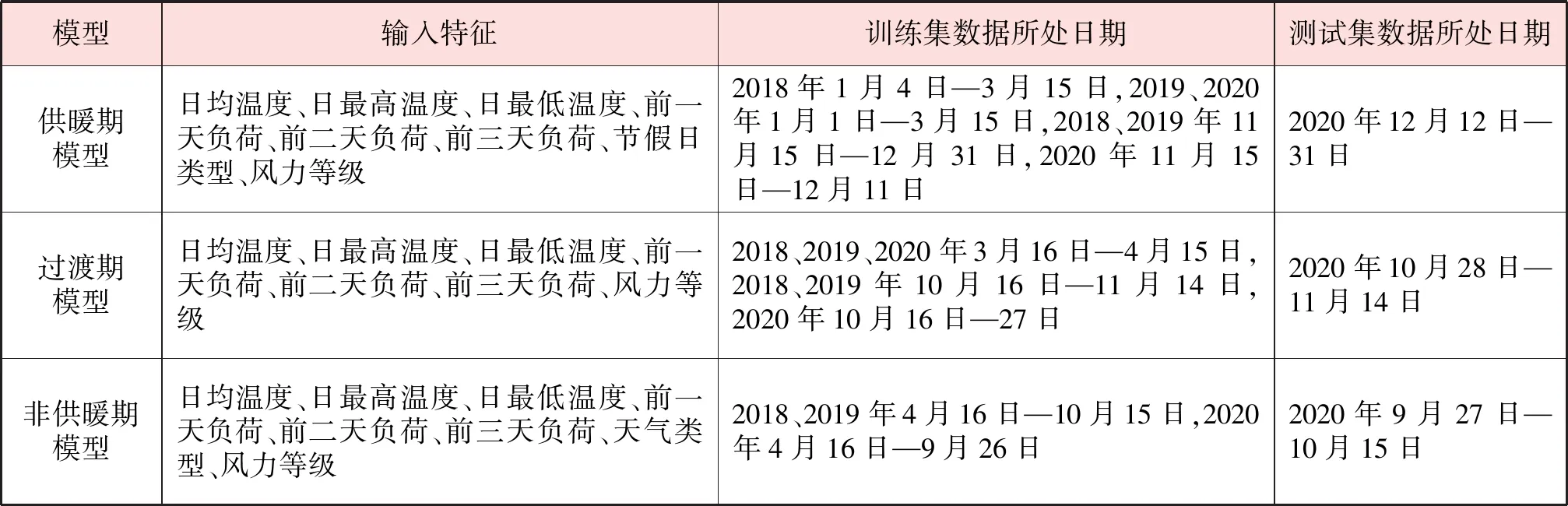
表6 3个时期模型的输入特征和训练集、测试集数据所处日期

力，同时选取BP神经网络模型(简称BP模型)、单一LSTM模型(简称LSTM模型)以及支持向量机模型(简称SVM模型)分别进行3个时期的日负荷预测，计算得到平均绝对百分比误差，并与Dropout-LSTM 模型的平均绝对百分比误差进行对比，结果见表7。3个时期不同模型部分燃气日负荷预测值见图4～6。

表7 4个模型预测平均绝对百分比误差 %

图4 2020年供暖期不同模型部分燃气日负荷预测值对比

图5 2020年过渡期不同模型部分燃气日负荷预测值对比

图6 2020年非供暖期不同模型部分燃气日负荷预测值对比

由表7可看出，BP模型预测效果较差；SVM模型对解决小样本问题有明显优势[16]，因此在本文数据较少的情况下预测效果较好；Dropout-LSTM模型的平均绝对百分比误差最小，是所有模型中预测效果最好的。

由图4～6可以看出，每个时期4种模型的预测值与真实值的变化趋势基本一致，表明选取的输入特征是合理的。

此外，供暖期是一年中燃气日负荷最大的时期，燃气主要用于供暖，用气规律性强，4种模型对供暖期日负荷的预测精度是最高的；过渡期的日负荷波动程度大，负荷特性难以提取，部分日期的预测值与真实值产生较大偏离，导致预测效果不如其他两个时期。

⑤ 不划分时期的日负荷预测

将把全年划分为3个时期的预测模型称为分时期预测模型。为进一步证明分时期预测模型具有较高的适用性和预测精度，现建立不划分时期的全年预测模型，仍对同时段的燃气日负荷进行预测。将3 a全部数据进行相关性分析，结果见表8。

表8 全年燃气日负荷与影响因素的Pearson相关性分析

选日均温度、日最高温度、日最低温度、风力等级、前一天负荷、前二天负荷、前三天负荷作为输入特征，将2018年1月4日—2020年9月30日的数据作为训练集，对2020年10月1日—10月15日、11月1日—11月14日、12月16日—12月31日的日负荷进行预测。分时期预测模型与全年预测模型的平均绝对百分比误差见表9。

表9 分时期预测模型与全年预测模型的平均绝对百分比误差

由表9可以看出，与分时期预测模型相比，全年预测模型的预测效果较差，表明将全年数据进行整体分析建模不能有效描述所有日期的用气情况。

6 结论

① 将全年分为供暖期、过渡期和非供暖期3个时期，3个时期的燃气日负荷都与日均温度、日最高温度、日最低温度、前一天负荷、前二天负荷、前三天负荷呈强相关性。供暖期日负荷与节假日类型和风力等级呈弱相关性，与天气类型和星期类型无相关性；过渡期日负荷与风力等级呈弱相关性，与天气类型、星期类型和节假日类型无相关性；非供暖期日负荷与天气类型和风力等级呈弱相关性，与星期类型和节假日类型无相关性。

② Dropout-LSTM模型可以很好地预测城市燃气日负荷，比BP模型、LSTM模型以及SVM模型有更好的预测效果。

③ 与基于全年数据的全年预测模型相比，分时期预测模型预测精度更高。

④ 供暖期的燃气日负荷规律性强，对供暖期的日负荷预测精度最高，非供暖期次之，由于过渡期日负荷波动大，预测效果是3个时期中最差的。