卷积神经网络模型的遥感反演水质参数COD

李爱民， 范 猛， 秦光铎， 王海隆， 许有成

1. 郑州大学地球科学与技术学院， 河南 郑州 450001 2. 郑州大学水利科学与工程学院， 河南 郑州 450001

引 言

随着社会经济的高速发展， 一些地表水体(湖泊、 水库和河流)受到了严重的污染。 全面准确的水质监测是水污染治理和水环境保护的前提。 传统水质监测方法主要是现场采集水样， 实验室测量各种水质参数， 难以反映污染物的空间分布特征及水质参数浓度的大面积范围的动态变化[1-2]。

随着国内外卫星遥感数据源的不断丰富， 遥感被广泛应用于水质动态监测。 目前利用遥感数据反演的水质参数多集中于叶绿素a[3-5]、 悬浮物[6]以及CDOM[7]等； 随着对水质光谱特征研究的深入， 机器学习算法的引用、 以及遥感技术的不断革新， 利用遥感手段反演的水质参数种类不断增加， 其中化学需氧量(chemical oxygen demand, COD)的反演近年来得到广泛关注； COD是反映水中有机污染程度的重要指标， 准确评估和掌握水体COD浓度分布对污染治理和环境保护有重要作用。 目前在COD参数遥感反演方法中应用最多也最广泛的是经验分析方法[8]， 即以遥感影像“面”值与实际水样采集的“点位”值建立函数关系， 如赵起超等[9]基于Landsat8影像， 使用BP神经网络方法反演白洋淀水体的COD浓度， 平均相对误差为16.5%。 目前利用多光谱遥感数据反演COD浓度精度较低， 一是因为经验方法是以皮尔逊相关系数大小为衡量指标选取建模波段， 对于多光谱遥感数据而言， 其光谱波段范围较宽， 波段的组合数量有限， 难以找到相关系数高的变量作为自变量； 二是由于遥感影像的“面”和实测数据“点”之间存在空间尺度上的差异， 以及遥感图像处理中几何校正、 大气校正等因素的影响， 均导致对模型的建立以及模型的迁移应用产生较大影响。

近年来深度学习技术快速发展， 在遥感领域得到了广泛的应用， 不同结构的卷积神经网络在遥感影像语义分割[10-11]、 目标检测[12]、 以及遥感影像去噪[13]等方面取得了巨大的进展。 深度卷积神经网络是将卷积理论与人工神经网络相结合， 通过数据特征提取及参数共享等机制实现输入和输出数据之间的非线性关系映射[14]。 将深度卷积神经网络用于水质参数定量遥感反演中， 有望为遥感水质参数反演提供一种新的解决方案。

基于多光谱高分辨率Planet卫星影像， 采用卷积神经网络对郑州市天德湖COD水质参数进行遥感反演， 并利用若干反演模型进行精度对比分析， 以期对卷积神经网络在定量遥感反演中的应用做一些探讨。

1 实验部分

1.1 研究区与数据源

选择河南省郑州市天德湖(34°48′—34°49′N， 113°29′—113°30′E)作为研究区， 湖区面积约为0.306 km2， 水深2～10 m。 实地水样采集时间为2020/12/05日上午。 采用Planet卫星数据； 遥感影像数据通过北京国测星绘信息技术有限公司购买(http://www.satimage.cn/)。 卫星在研究区成像时间与水样采集时间同步， 遥感影像有4个光谱波段， 分别是蓝波段(455～515 nm)； 绿波段(500～590 nm)； 红波段(590～670 nm)； 红外波段(780～860 nm)。 影像级别为L1B， 分辨率为4 m， L1B级数据为基础产品， 获取的数据经过了几何校正和辐射校正等处理。

1.2 水样采集检测与实测光谱分析

在研究水域内共采集38个样本， 采样时乘坐皮划艇小船， 由若干名人员协作采集， 在湖面无波动时利用3L的有机玻璃采样器采集深度为0～50 cm的表层水样。 将采集的水样放置在阴冷处， 并当天带回实验室进行指标测试。 COD浓度的测定采用密闭催化消解法， 利用5B-6C快速测定仪测定水样的COD浓度， 测得的COD浓度范围为6.53～39.13 mg·L-1， 平均值为24.22 mg·L-1， 标准差为6.78 mg·L-1。 研究区及采样点如图1所示。

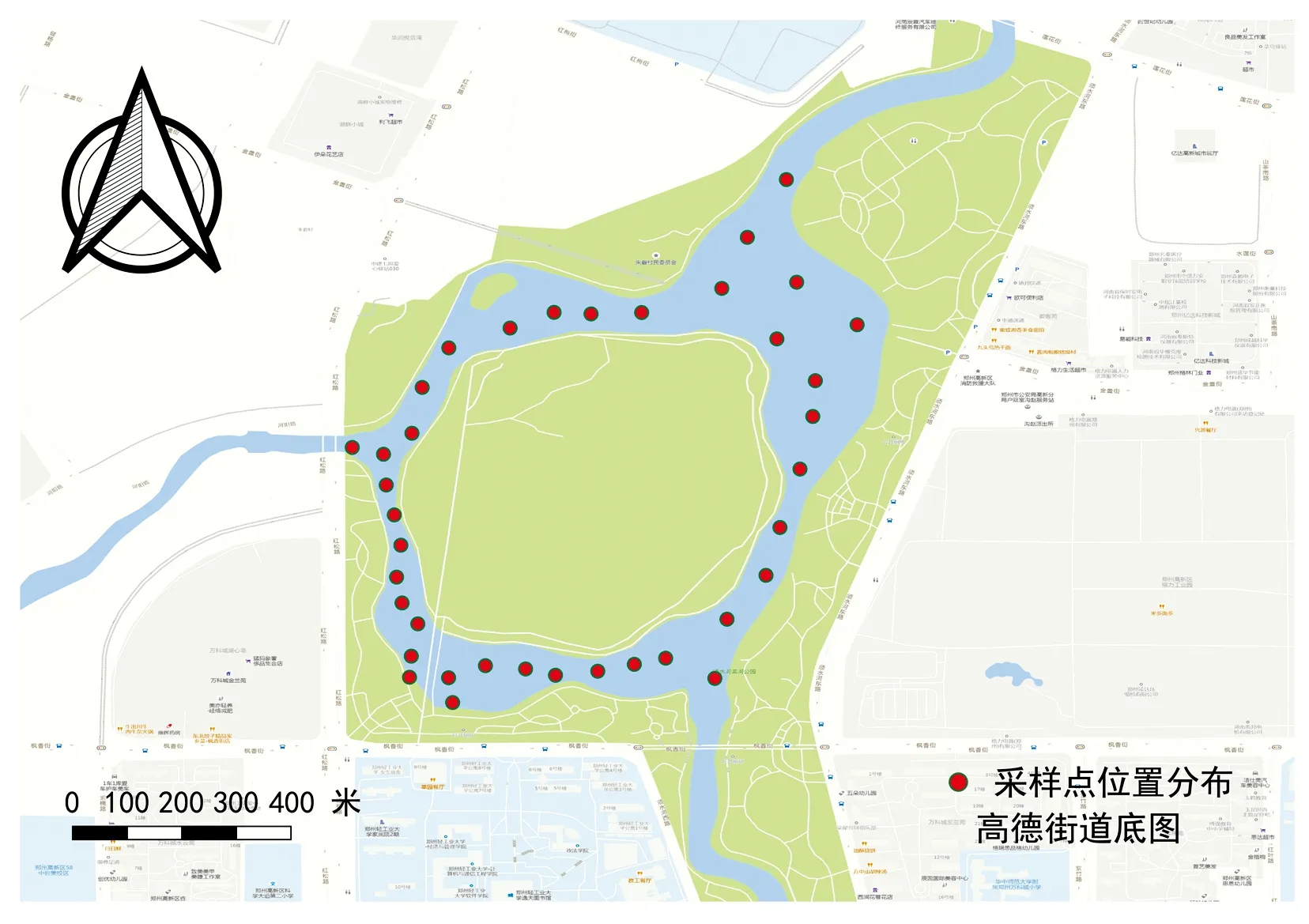
图1 研究区及采样点位置Fig.1 Study area and location of sampling points

同步开展水面高光谱数据测量。 采用美国ASD公司生产的FiledSpecHH2手持式光谱仪， 在采集水样之前对仪器进行校正， 采用水面以上测量法进行水面光谱测量， 并对每个采样点采集10次取平均值作为此采样点的光谱反射率数据。 实测光谱曲线如图2所示， 为和Planet影像数据光谱范围保持一致， 选取400～900 nm范围内的光谱曲线进行分析。 由图2可看出， 由于水体对太阳辐射具有强烈的吸收作用， 使遥感反射率值大多较低。 天德湖水体具有典型的内陆水体特征， 其水体光谱变化带有较为明显的叶绿素a的光谱特征和悬浮物的光谱特征， 即在675 nm附近处有叶绿素a的吸收峰以及在700 nm附近处有叶绿素a和悬浮物叠加作用形成的反射峰， 而由于悬浮物的影响使440和550 nm附近处的叶绿素a的吸收峰和绿色反射峰不明显， 整体表现为中间高两端低。

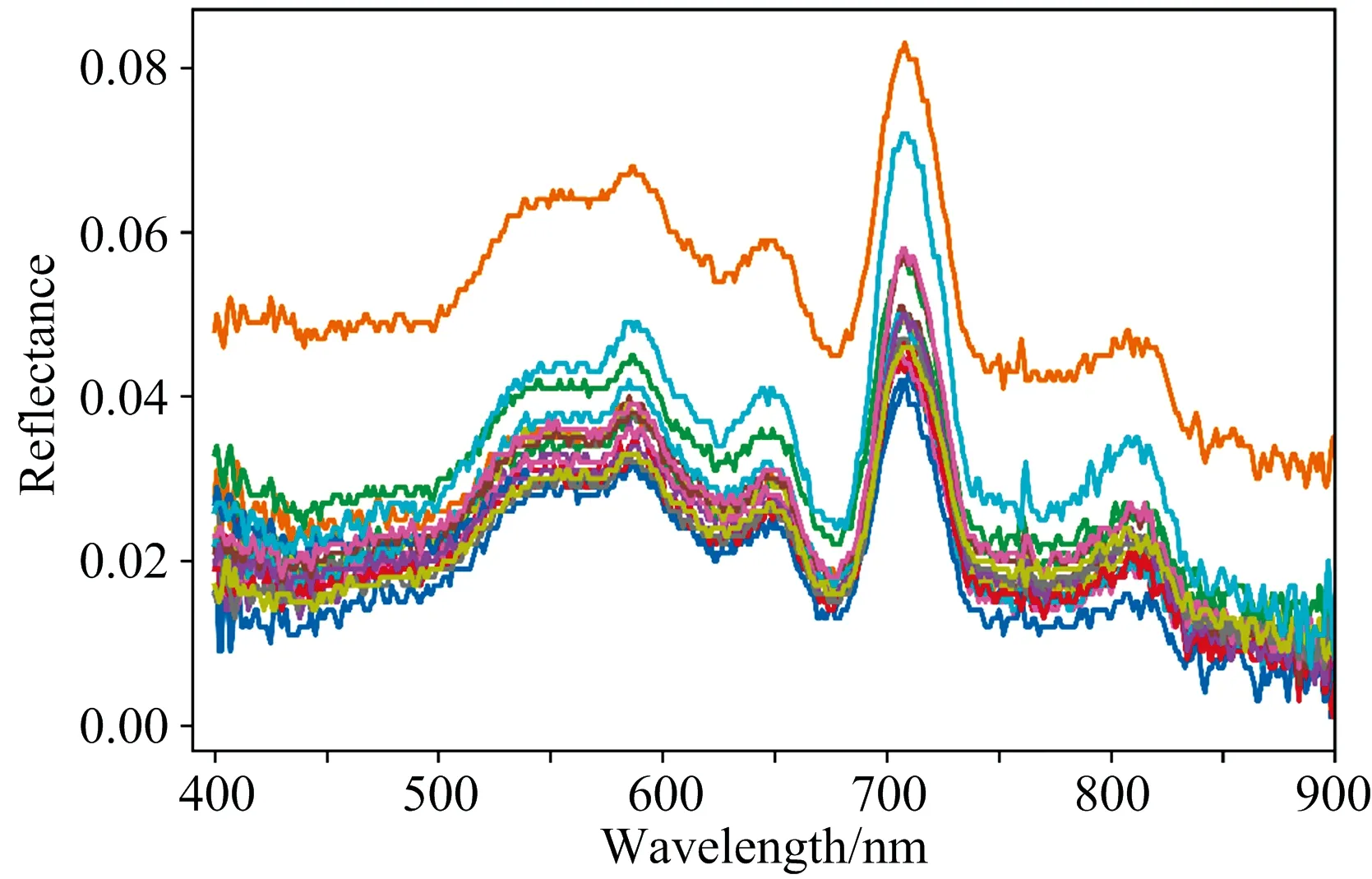
图2 实测光谱曲线Fig.2 Measured spectra

遥感数据值和实测的水质参数之间具有非常复杂的非线性关系， 深度学习方法能够学习到更深层次的像元之间的抽象关系， 这对于水质参数的反演有着新的启发， 因而探索将卷积神经网络用于水质参数反演意义重大， 在内陆水体水质参数反演精度方面具有巨大的潜力。 实验采用卷积神经网络方法针对Planet卫星数据进行COD反演， 同时建立单变量回归(一元线性回归、 幂函数回归)、 多变量回归(主成分回归、 多元线性回归)以及多隐含层神经网络回归模型进行对比， 采用均方根误差(root mean square error, RMSE)、 决定系数(coefficient of determination,R2)进行精度评价。

1.3 建模波段选择

以经验分析为主的水质参数反演多以皮尔逊相关系数大小为衡量标准， 从遥感影像波段的不同组合形式中选取其最优波段进行反演建模， 对不同波段组合的形式进行相关系数计算， 不同波段组合的最高相关系数记录如表1所示， 根据单变量建模和多变量建模， 分别选择合适的建模波段进行回归建模。 分析得出， 在不同波段组合后的变量之间也存在较高的相关性， 故在筛选波段中选取了5个波段组合方式参与多变量建模(表1)。

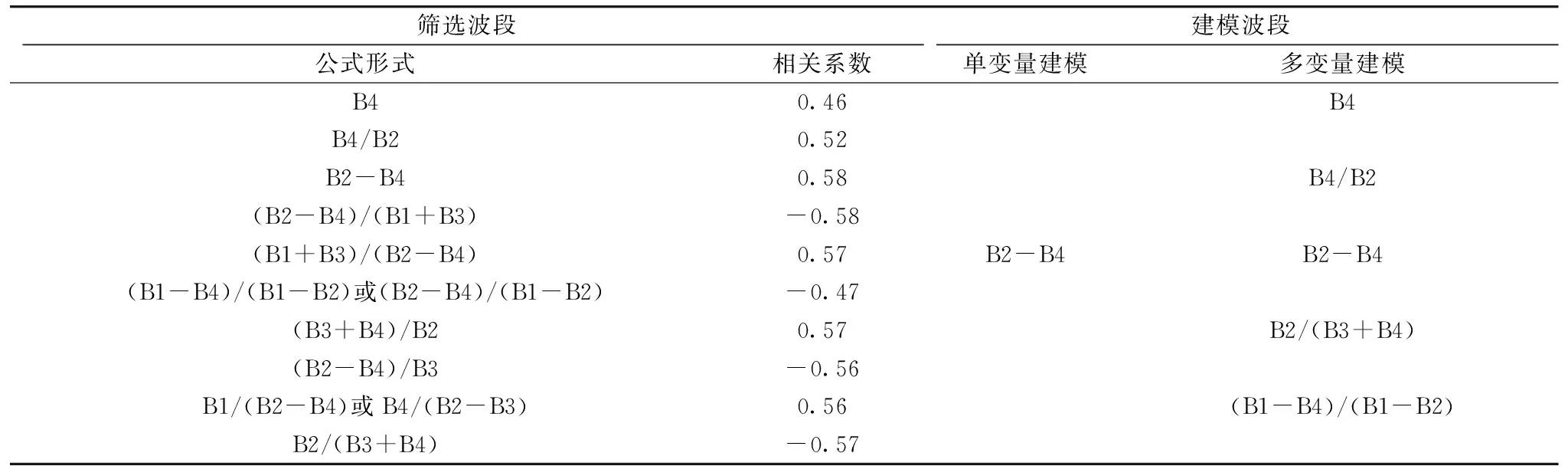
表1 相关系数计算Table 1 Calculation of correlation coefficient

1.4 卷积神经网络构建

卷积神经网络(convolutional neural networks, CNN)是一类包含卷积计算且具有深度结构的前馈神经网络(feedfor-ward neural networks)， 是深度学习(deep learning)的代表算法之一。 卷积神经网络具有表征学习(representation learning)能力， 能够按其阶层结构对输入信息在更高层次进行抽象， 获取深层次的图像信息。 本研究建立“卷积-池化-全连接”的卷积神经网络结构， 探讨卷积神经网络在水质参数反演中的应用。 考虑到训练集样本有限， 对原始获取的遥感影像进行正射校正处理， 将正射校正前的影像用38个采集点坐标裁剪出38个Patch图像(7×7)加入到训练集中， 以此对训练集进行增强处理， 按8∶2比例将数据划分为训练集和测试集。

为尽量避免过拟合现象， 在卷积神经网络训练中加入dropout和early stop策略， 选择Adam算法对学习率进行优化， 激活函数选择ReLu， 输出层的损失函数选择均方误差(means qured error， MSE)， 在模型训练中将训练集按7： 3的比例划分为新训练集和验证集。 模型的结构如图3所示。

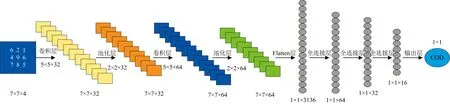
图3 卷积神经网络的结构Fig.3 Structure of convolutional neural networks

卷积层的工作原理是利用卷积核进行深层次抽象特征的提取， 核大小为5×5， Padding为“Same”， 池化层是对来自卷积层的数据进行不同方式的采样处理， 核大小为2×2， Padding方式为“Same”， Flatten层是将所有特征拉伸成一维的形式。

卷积神经网络反演COD水质参数的工作流程如图4所示。

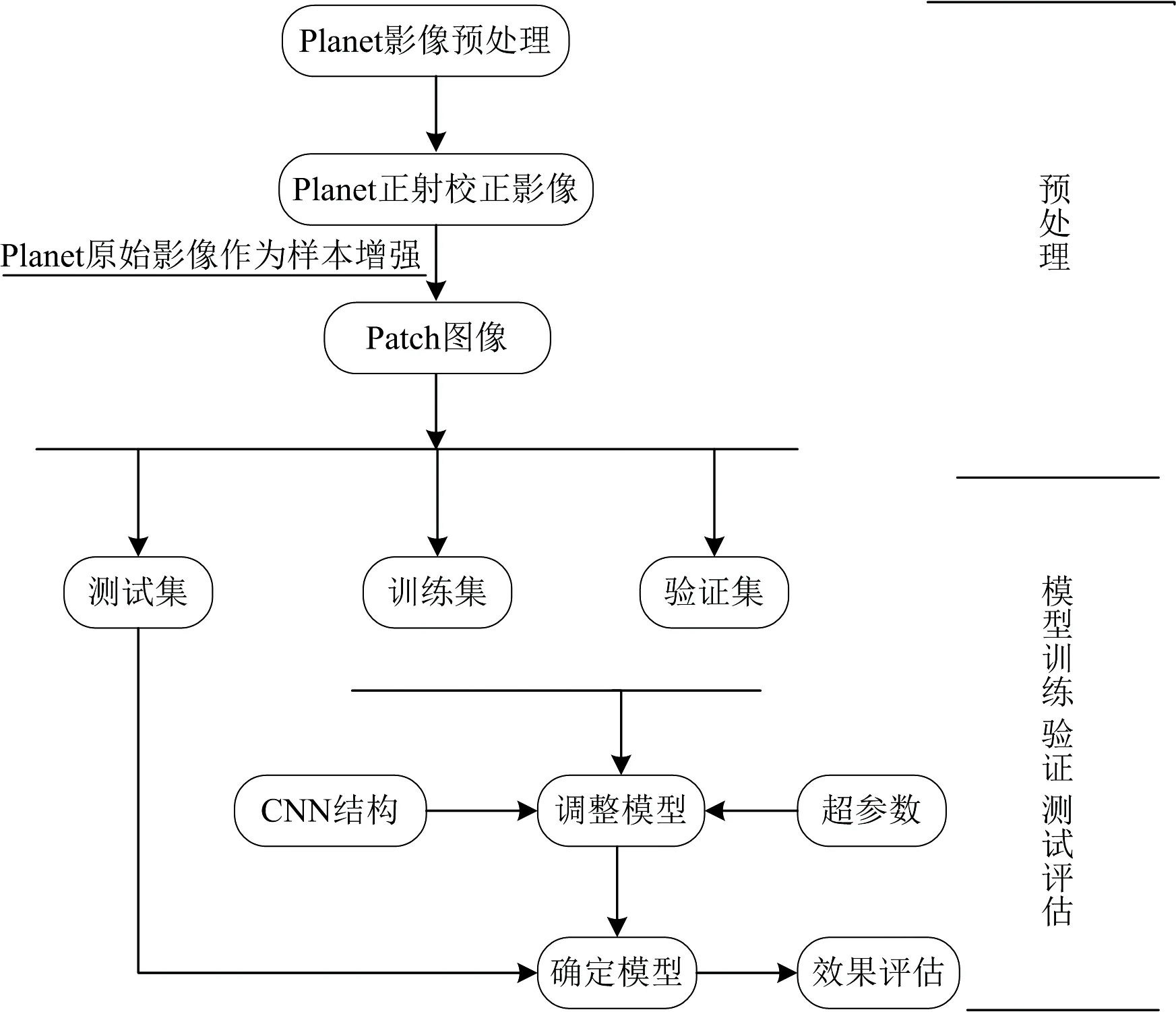
图4 卷积神经网络反演COD工作流程Fig.4 Workflow of COD retrieval by convolutional neural network

2 结果与讨论

2.1 模型训练与精度评估

单变量回归选择一元线性回归、 乘幂函数模型、 指数模型； 多变量回归选择主成分回归、 多元线性回归以及多隐含层神经网络回归模型。 多隐含层神经网络训练中采用网格搜索确定隐含层个数和每层的神经元个数， 最终确定隐含层为两层， 每层的神经元个数分别是6个和8个。 在卷积神经网络结构确定中采用多次实验调节卷积层、 池化层以及全连接层中的核大小， 步长， 神经元个数等超参数， 并结合early stop和dropout等策略来尽量避免过拟合， 其模型最终确定的网络结构如图3所示。

将建立的多个模型进行汇总， 如表2， 无论是单变量回归还是多变量回归模型， 其精度都较低， 其根本原因是遥感影像数据和水质参数浓度之间的关系是非线性关系， 用皮尔逊相关系数难以准确衡量之间的相关性， 且在建立多变量回归模型中的建模波段之间也存在较高的相关性， 故以常规方法建立的模型精度普遍较低， 其中卷积神经网络精度最高， 其决定系数为0.89， RMSE为2.22 mg·L-1， 其次为多隐含层神经网络， 其决定系数为0.76， RMSE为3.45 mg·L-1， 而其他的单变量回归和多变量回归模型的精度均较差。

表2 几种COD反演模型及精度Table 2 Several retrieval models for COD and their accuracy

2.2 水质参数反演

将精度最高的卷积神经网络和精度最低的一元线性反演专题图进行对比， 如图5(a)和(b)， 天德湖的COD浓度分布都呈现西部高、 东部低、 东南方向的进水口浓度较低、 东北方向的出水口浓度较高的特征， 但卷积神经网络反演的专题图与实际情况更为符合， 反演的天德湖区域COD浓度平均值为23.96 mg·L-1， 标准差为7.11 mg·L-1， 变异系数为0.29； 一元线性反演的天德湖区域COD浓度平均值为26.92 mg·L-1， 标准差为8.71 mg·L-1， 变异系数为0.32， 可知卷积神经网络反演结果更接近实际采样点的统计值， 其实际采样点浓度平均值为24.22 mg·L-1， 标准差为6.78 mg·L-1， 变异系数为0.28。 由图6(a)知， 一元线性模型反演结果在实测浓度高于25 mg·L-1时会存在严重的高估， 低于25 mg·L-1时存在低估现象， 由图6(b)知， 一元线性模型的浓度值分布较为集中， 卷积神经网络反演结果的直方图浓度变化较为平缓， 过渡更加自然。

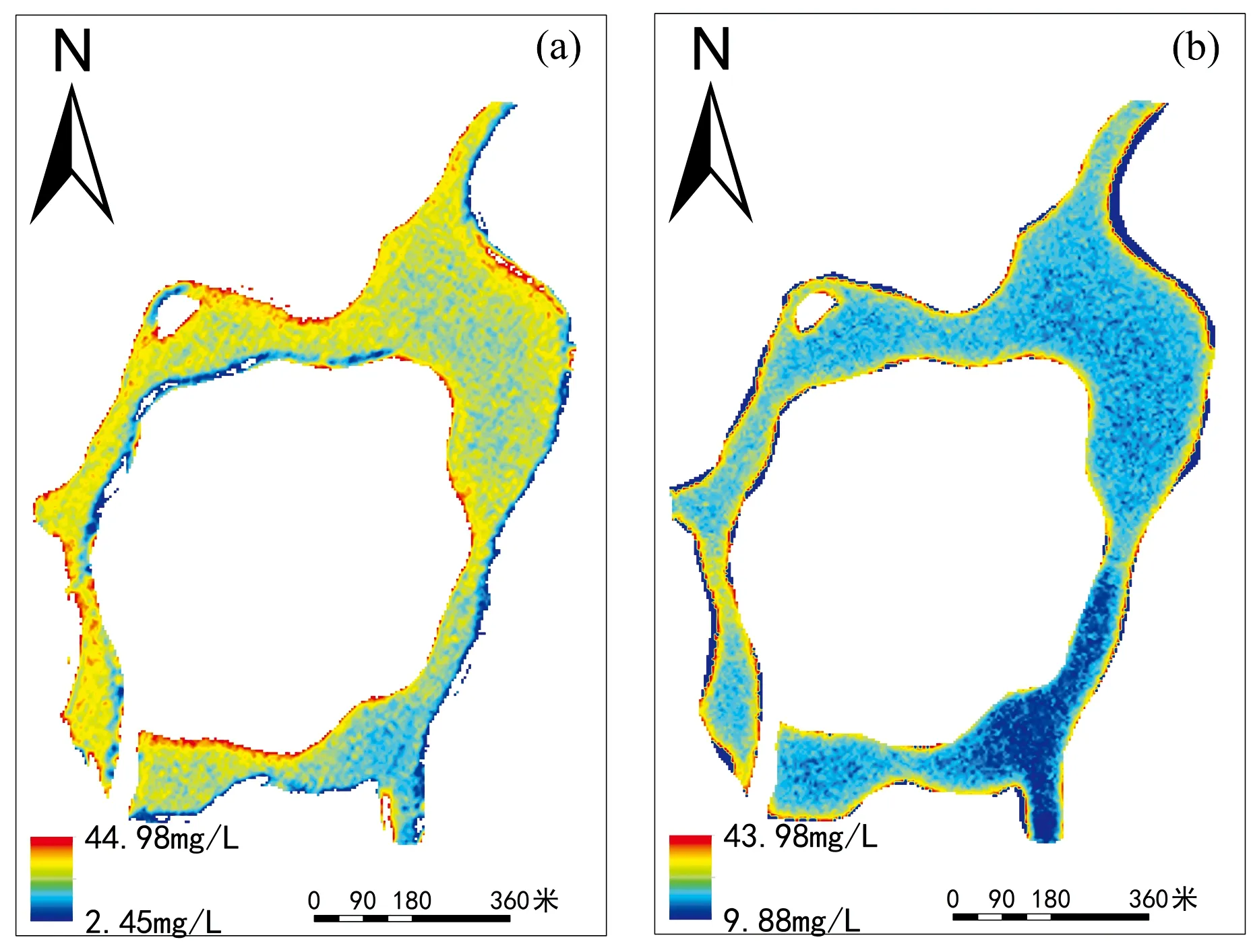
图5 两种模型反演专题图对比(a)： 卷积神经网络反演专题图； (b)： 一元线性反演专题图Fig.5 Contrast of two retrieval thematic maps(a)： Convolutional neural networks thematic map； (b)： Unary linear inversion thematic map

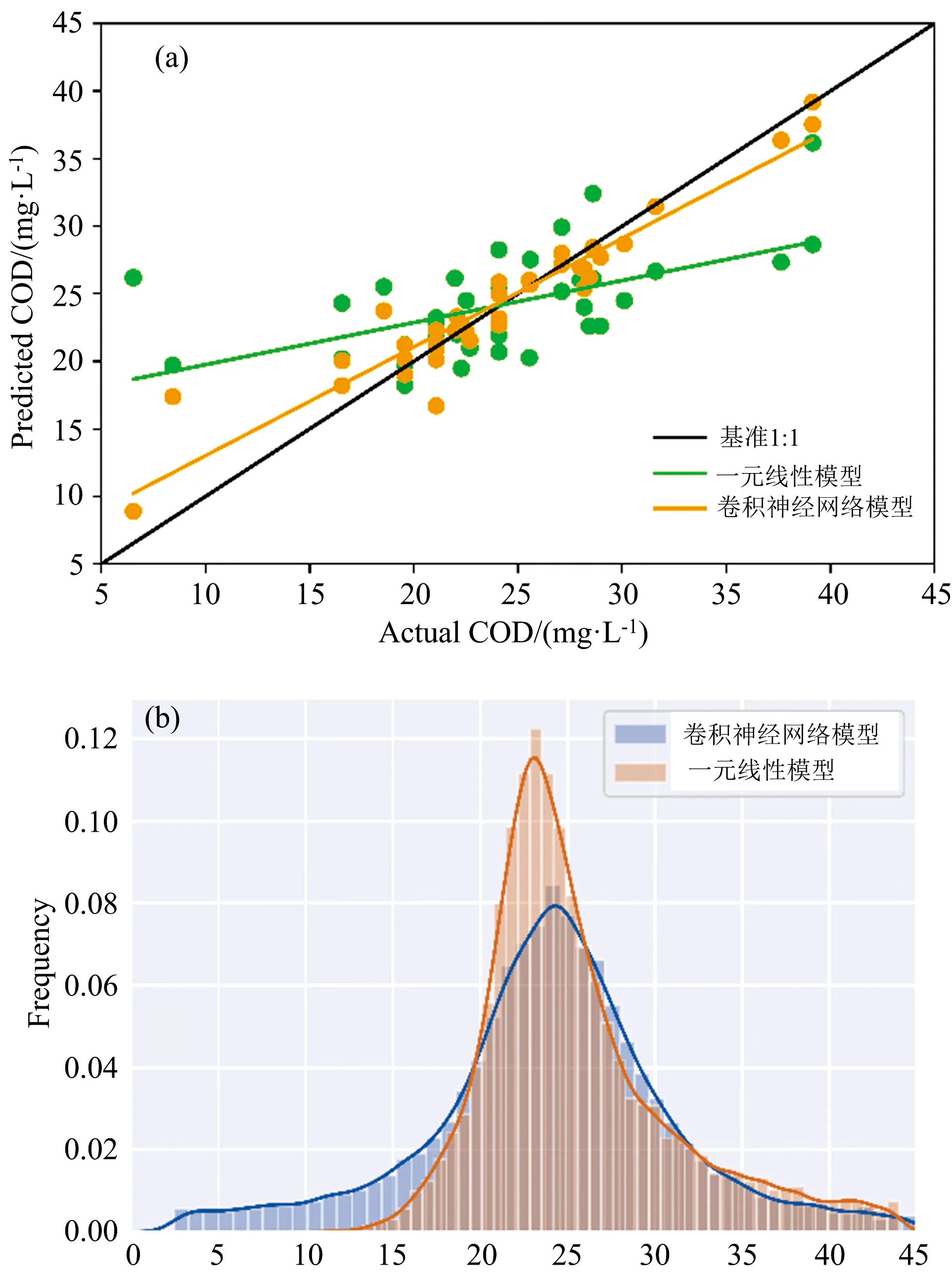
图6 两种反演模型对比分析(a)： COD实测值和预测值； (b)： 反演结果的直方图Fig.6 Contrastive analysis of two retrieval models(a)： Actual and predicted values of COD； (b)： Histogram of retrieval results

3 结 论

基于Planet多光谱高分辨率遥感影像， 利用卷积神经网络和传统模型对天德湖COD水质参数进行反演， 分析模型精度， 反演得到天德湖水质参数COD浓度分布专题图。 其主要研究结论如下。

(1)相比于常规以皮尔逊相关系数为衡量标准选择不同波段组合的反演方式， 卷积神经网络反演具有更高的空间反演精度， 其决定系数为0.89， RMSE为2.22 mg·L-1， 这是因为卷积神经网络能够提取以目标像元为中心的领域空间信息， 自动学习遥感数据的“内在规律”， 在一定程度上避免传统方法建模带来的不稳定性。

(2)天德湖的COD浓度空间分布呈现西部高、 东部较低、 东南方向的进水口浓度较低、 东北方向的出水口浓度较高的特征。 卷积神经网络反演的天德湖区域浓度平均值为23.96 mg·L-1， 标准差为7.11 mg·L-1， 变异系数为0.29， 更加接近实际采样点的统计值。

建立的卷积神经网络仍存在改进的空间， 如将遥感影像进行旋转、 反转等方式对样本进行增强， 增加卷积神经网络的深度以及讨论不同核大小对模型的影响等， 将在以后对模型进行改进， 以期取得更好的反演效果。 现阶段的反演结果中的每个像元的水质参数浓度值比较精确， 但依然处在从反演结果的专题图中获取水质参数浓度的空间分布范围和变化趋势的阶段。 随着近年来反演技术的进步， 反演的要求将逐渐从全局浓度变化趋势分析向局部反演的准确性方面转变， 在此背景下以卷积神经网络模型为代表的机器学习模型在水质参数反演中具有较高的应用潜力。

致谢：此次野外实验的数据获取得到了研究生赵刘义、 李亭亭、 王革林的帮助， 在此表示衷心的感谢!