基于二次-四次谐波联用的免标定波长调制激光吸收光谱方法

王一红， 周 宾， 赵 荣， 汪步斌

东南大学能源与环境学院， 能源热转换及其过程测控教育部重点实验室， 江苏 南京 210096

引 言

可调谐激光二极管吸收光谱技术因其高灵敏度、 高选择性和快速响应的特点， 被广泛应用于痕量气体的检测与燃烧诊断研究[1-4]。 在信号检测方法上常采用波长调制光谱(wavelength modulation spectroscopy, WMS)技术。 为了实现浓度、 温度等气体参数的定量测量， 通常需用标气对数据进行标定， 然而由于测量环境变化， 标定结果会存在偏差。 对于航空发动机燃烧诊断等恶劣的测量环境， WMS技术的标定工作往往无法实现， 因此免标定测量方法一直是WMS技术的研究热点问题[5-6]。

Sun等[7]提出的基于WMS-2f/1f波形拟合的测量方法极大的拓展了WMS技术的应用。 然而WMS-2f/1f波形拟合法需要大量迭代计算， 每一步迭代都需要进行滤波和最小二乘拟合处理， 测量实时性难以保证。 为了提高计算效率， 研究人员从谐波波形分析的角度提出了一系列免标定WMS方法。 Russell等[8]提出了从二次谐波计算吸收展宽的方法， 但该方法只适用于很小的调制系数m。 Duffin等[9]在调制系数很小(m<2.2)的情况下， 通过一次谐波信号得到了气体的分子吸收线型， 然而该方法并不适合弱吸收情况， 且在大调制系数时需要进行复杂的修正。 Peng等[10]提出了利用奇次谐波提取吸收线型的方法， 然而该方法在大调制系数下需要计算高次谐波， 加大了计算量。 张书锋等[11]发现二次和四次谐波峰值比具有恒过不动点的特征， 基于该不动点提出了一种新的免标定WMS方法， 然而该方法只适用于弱吸收的情况。 Chen等[12]提出了一种基于零次、 二次、 四次谐波高度的免标定WMS方法， 然而该方法只适用于Lorenz线型， 且零次谐波容易受到低频噪声的干扰。 Wang等最近提出了一个基于非零偶次谐波的非拟合WMS方法[13]， 适用于更一般的Voigt谱线线型， 通过简单的代数计算即可获得温度、 浓度等关键参数。 然而该方法至少需要三次滤波计算， 如何从更少的谐波中提取有效信息， 对提高计算效率有着重要意义。

在对WMS方法进行详细理论分析的基础上， 提出了一种新的基于二次-四次谐波的免标定WMS方法。 该方法适用于任意调制系数和光学厚度， 通过二次-四次谐波高度的比值可以唯一的确定调制系数m， 然后根据任意的偶次谐波高度计算获得积分吸收面积， 进而得到气体的浓度值。 在实验室搭建WMS测量系统， 开展室温下CH4浓度的测量实验， 并通过Allan方差评估该方法的可靠性和精确性。

1 测量原理

1.1 理论基础

在激光器低频正弦扫描吸收谱线的基础上， 对激光器注入高频正弦调制信号， 此时激光的瞬时入射光强I0(t)可以用式(1)数学模型表示

(1)

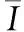
(2)

It(t)=I0(t)exp{-α[ν(t)]}

(3)

式(3)中，α[ν(t)]为光谱吸收率

α[ν(t)]=PxS(T)Lφ[ν(t)]=Aφ[ν(t),ν0,γL,γG]

(4)

式(4)中，P[atm]为气体总压；x为气体分子的体积分数；S(T)[cm-2·atm-1]为温度T[K]下的谱线线强；L[cm]为吸收光程长；A=PxS(T)L[cm-1]为积分吸收面积；ν0[cm-1]为吸收谱线中心频率；γL[cm-1]和γG[cm-1]分别为Lorenz线型和Gauss线型的半高全宽；φ(ν,ν0,γL,γG)为Voigt线型函数， 是Lorenz线型函数φL(ν,ν0,γL)和Gauss线型函数φG(ν,ν0,γG)的卷积。

通过对光强信号对数变换得到的光谱吸收率信号的谐波分析可以实现气体参数的免标定测量[13]， 光谱吸收率α[ν(t)]的n次谐波峰高为(n为偶数)

(5)

式(5)中，m为调制系数；γ为谱线的线宽;ε0=1,εn=2 (n≥1);cL和cG分别为Lorenz展宽γL和Gauss展宽γG的权重系数;In/2(·)为第一类n/2阶变形Bessel函数。

1.2 基于偶次谐波中心峰高的气体参数测量方法

定义Lorenz调制系数mL=2aM/γL和Gauss调制系数mG=2aM/γG， 根据Olivero-Longbothum展宽模型[14]可知mL,mG,m之间满足式(6)关系

(6)

显然γL<γ,γG<γ， 即mL>m,mG>m， 根据这一限制条件可以反解得到mL的表达式如式(7)

(7)

由式(5)可知，α[ν(t)]的任意两个不同的偶次谐波(n,k为偶数， 且n≠k)峰高的比值Rn, k为

(8)

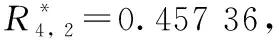
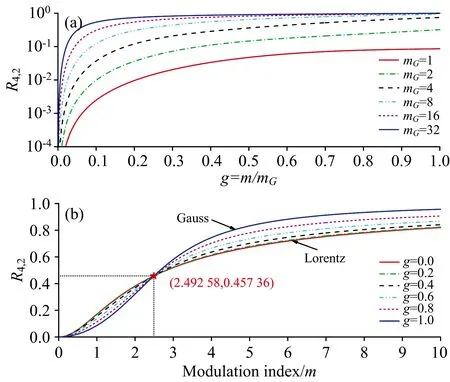
图1 四次和二次谐波峰高比R4, 2与调制系数m的关系(a): R4, 2-g曲线; (b): R4, 2-m曲线Fig.1 Ratios of H4 and H2, i.e. R4, 2, versus m(a): R4, 2-g curves; (b): R4, 2-m curves

为了利用四次谐波与二次谐波的中心峰高比值R4, 2来计算调制系数m， 需要已知mG或者g。 实际上对于气体浓度测量， Gauss展宽γG可根据气体温度T[K]计算得到

(9)

式(9)中，ν0[cm-1]为吸收谱线中心；M为相对分子量。 调制深度aM可以通过测量标准具信号得到， 因此mG是容易获得的。 已知mG后， 采用式(8)即可求解调制系数m， 根据γ=2aM/m及式(5)可得积分吸收面积。 最终可以计算得到气体的摩尔分数x

(10)

2 实验部分

2.1 谱线选择

根据HITRAN2016数据库[15]可知CH4在波长1 653.73 nm(6 046.95 cm-1)附近有三个紧邻的谱线(参数见表1)。 CH4吸收峰的数值仿真结果如图2(a, b, c)所示，

表1 CH4在6 046.95 cm-1附近的吸收谱线参数Table 1 Parameters of CH4 spectroscopic transition lines around 6 046.95 cm-1 in HITRAN2016 database

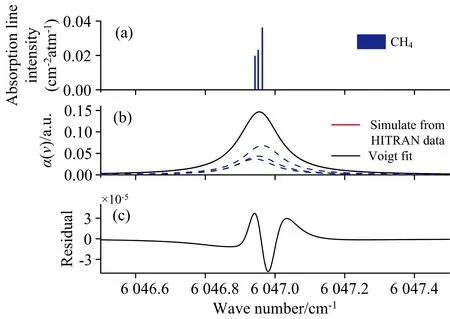
图2 甲烷吸收光谱仿真(x=2%, P=1 atm, L=20 cm, T=296 K)(a): 吸收谱线位置; (b): 吸收光谱的Voigt线型拟合; (c): 拟合残差Fig.2 Simulated methane absorption spectroscopy(a): Line transitions; (b): Voigt fitting of absorption spectra; (c): Residuals

在大气压下由于压力展宽的作用， 吸收谱线重合形成一个吸收峰， 用Voigt线型函数可以很好地逼近。 因此可以将该处的吸收谱线群当作孤立吸收谱线处理。

2.2 实验装置搭建

波长调制吸收光谱CH4浓度测量系统实验装置如图3所示。 激光光源采用1 653.7 nm分布反馈半导体激光器(NLK1U5EAAA, NTT)。 通过控制器(LDC501, SRS)对激光器的发射波长进行调制。 函数发生器(DG1062, RIGOL)产生适当的调制电压信号(fS=100 Hz,fM=20 kHz)对激光器发射波长进行调谐。 激光由光纤分束器分为三路， 第一路经准直器后通过充满CH4标准气体(浓度为2.00%)的吸收池(光程长20 cm， 温度284.6 K)， 透射光强被光电探测器(PDA10CS-EC, Thorlabs)接收； 第二路为参考光路， 不经过气体吸收池直接被光电探测器接收； 第三路通过固体光学标准具(马赫增德尔干涉仪, FSR=0.01 cm-1)后被光电探测器接收， 用于测量激光的时频响应特性； 探测信号由数据采集卡(PXIe-5170R, NI)记录， 透射光强和参考光强采样率为2 MSa·s-1， 标准具信号采样率为50 MSa·s-1。 吸收池置于温度控制箱中， 以保持甲烷吸收谱线稳定的线强度和线宽， 实现精确的气体浓度测量。

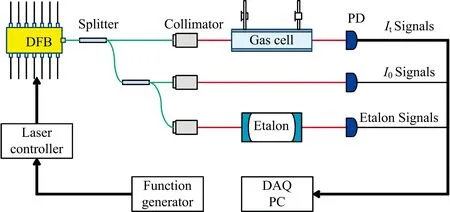
图3 实验装置Fig.3 Experimental setup

3 结果与讨论

为减小噪声对测量的影响， 首先对1 s内的光强信号进行平均处理， 平均后的透射光强及参考光强信号如图4(a)所示， 通过对光强信号的对数处理得到的信号{记为β(t)信号,β(t)=-ln[It(t)/I0(t)]}如图4(b)所示。 需要指出的是， 由于光纤分束器分光不均等原因导致透射光强与参考光强的幅值存在差异， 因此对数变换光强信号与光谱吸收率信号α[ν(t)]之间会相差一个直流量。 幸运的是， 直流量并不会影响光谱吸收率信号非零次谐波的分析， 因此在实验过程中无需对参考光路的光强幅值进行精确调整。

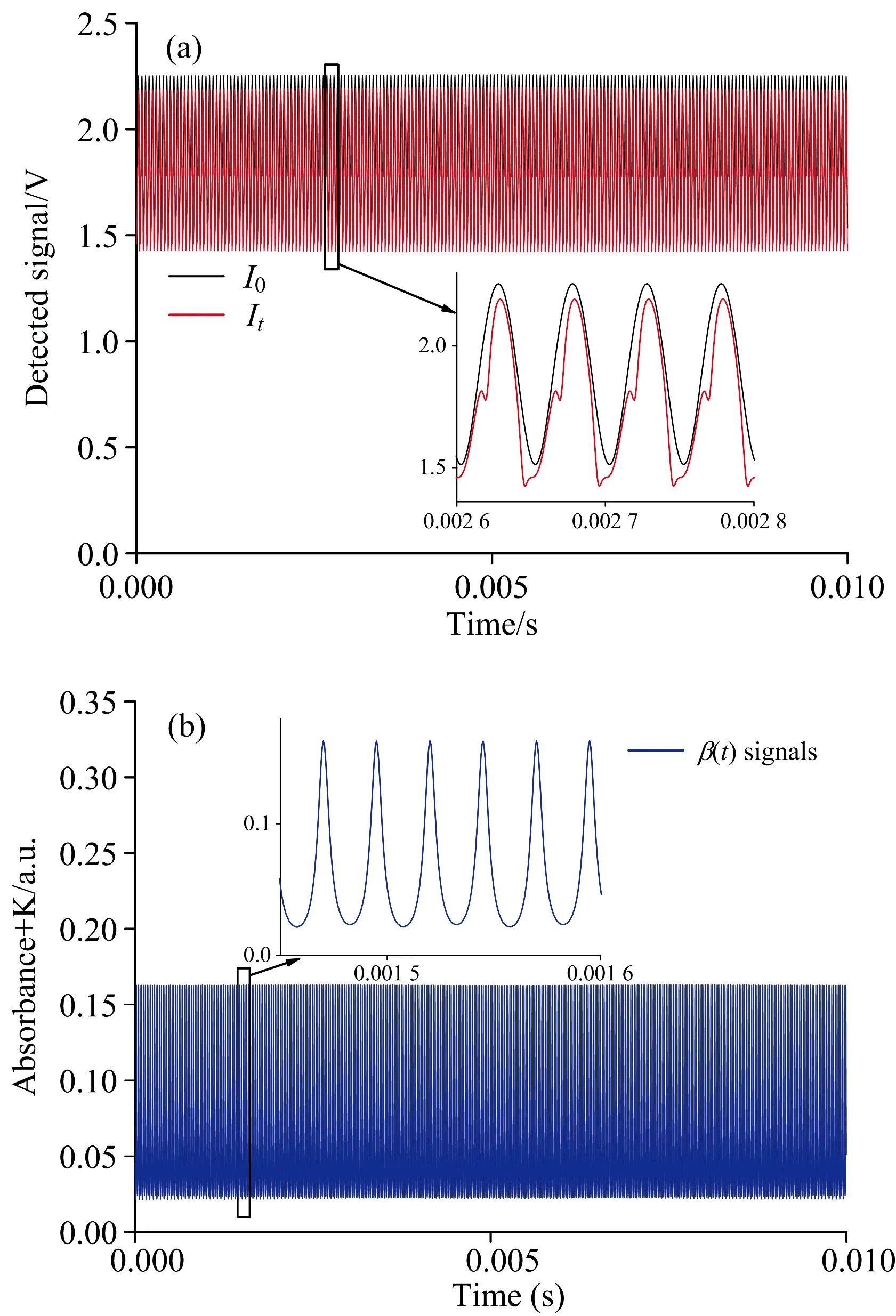
图4 测得的光强信号(a): 透射光强及参考光强信号; (b): 对数变换信号Fig.4 Measured laser intensity signals(a): Laser intensity; (b): Logarithmic-transformed signals, i.e.β(t)

光谱吸收率信号的FFT频谱如图5所示， 理论上截止频率选择fM/2才可以获得完整的谐波成分， 然而过大的截止频率会引入更多的噪声。 由于实验中采用的扫描电流强度很小， 因此二次谐波和四次谐波的频率成分非常集中， 可以选择较小的截止频率。

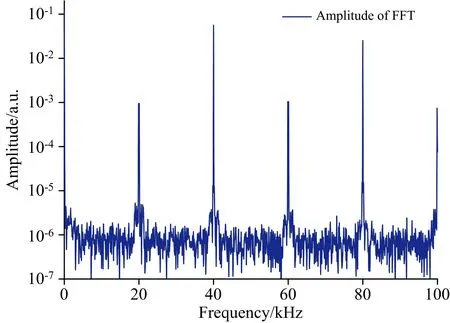
图5 光谱吸收率信号的FFT频谱Fig.5 The FFT spectrum of spectroscopic absorbance signal

不同截止频率下光谱吸收率信号的二次及四次谐波信号分别如图6(a,b)所示， 显然， 选择截止频率fc=10 kHz时， 会导致二次谐波和四次谐波信号引入较大的噪声， 而选择截止频率fc=400 Hz时， 二次谐波和四次谐波信号的幅值没有明显的差异， 却变得更加光滑， 这对谐波峰值高度的计算非常有利， 因此选择截止频率为fc=400 Hz。

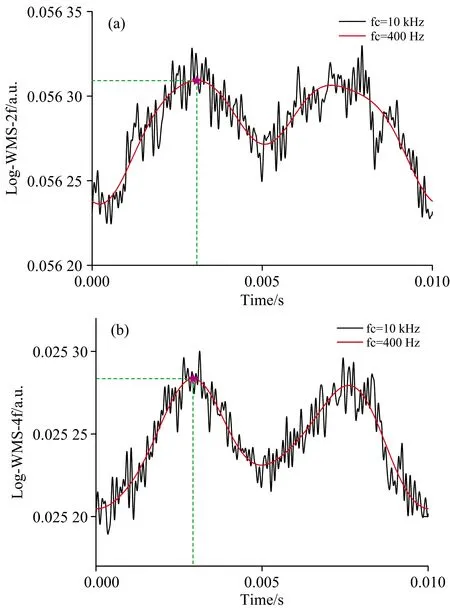
图6 不同截止频率下的谐波信号(a): 二次谐波; (b): 四次谐波Fig.6 Harmonic signals at different cut-off frequencies(a): 2f signals; (b): 4f signals

对浓度为2.00%的CH4标准气体进行5 min的连续测量， 浓度测量结果如图7(a)所示， 时间分辨率为1 s。 5 min内浓度测量值的平均值为2.023 9 %， 相对误差为1.19%。 通过分析Allan方差对系统探测灵敏度进行评估， 由图7(b)可知， 积分时间1 s时， 系统探测极限达到9.49×10-6； 积分时间为51 s时， 探测极限可达4.28×10-6。

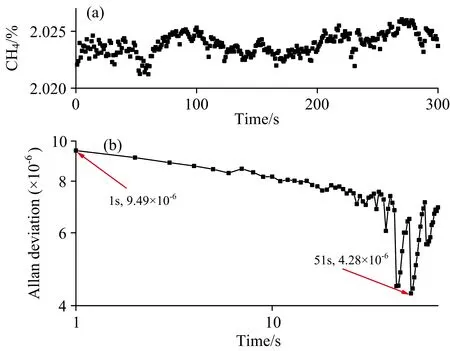
图7 WMS测量系统探测极限分析(a): CH4浓度测量值； (b): Allao方差分析Fig.7 Allan deviation analysis on WMS measurement system(a): CH4 concentrations; (b): Allan deviation plot of CH4 concentrations

4 结 论

提出了一种新的基于二次-四次谐波的免标定WMS方法。 该方法无需进行最小二乘迭代拟合计算， 降低了对硬件系统的要求； 不需要利用数据库中自展宽系数、 各种其他组分的碰撞展宽系数、 温度指数等过多的参数， 减小对数据库参数的依赖性； 由于只需要谐波的中心峰值， 此方法不需要扫描整个吸收谱线的形状， 应用范围更广， 例如适合高压和高温环境下的激波风洞或电弧加热的等离子体风洞等测量环境。 在实验室搭建WMS测量系统， 进行室温下CH4摩尔分数的测量实验， 实验结果表明该系统的测量相对误差为1.19%， 在20 cm吸收光程长下探测极限达到4.28×10-6， 验证了该方法应用于气体吸收光谱参数测量的可行性和精确性。