新型核电机器人伸缩臂的设计和有限元分析
卢明旭 唐德文
(1.南华大学 机械工程学院,衡阳 421001;2.核设施应急安全技术与装备湖南省重点实验室,衡阳 421001)
在我国众多的核电施工现场,需要提前铺设各种类型的钢管。因核电施工环境复杂,加之铺设钢管类型不同、管道运输困难等,核电施工现场存在管道安装效率低、吊装复杂且吊装载荷较低等问题,严重影响核电项目的施工进度和效果。因此,研发设计一种新型的核电现场专用管道吊装机器人对于提高我国核电管道安装效率具有重要意义。
目前,我国对于大型机器人伸缩臂的研究已取得一定进展。例如,吕娜[1]针对GT-750E汽车起重伸缩臂的设计进行展开性研究,得到了伸缩臂各类型截面的合理设计参数;高治理等[2]采用模块设计方法设计一种伸缩臂系统;齐建峰[3]对矿井专用液压变轨起重机机构展开研究,得到其稳定的动态性能。
尽管我国在化工、矿业、农业等方面都有专用的起重机器人,但是符合核电现场复杂施工环境的机器人却没有针对性设计研究。为此,本文设计一款全新的管道吊装伸缩臂,采用以力学计算、有限元分析相结合的方式,对起升机构部分的伸缩臂进行研究。通过对设计的新型核电机器人伸缩臂工作原理进行受力分析,开展伸缩臂在吊装过程中的仿真实验,校核其结构的应力情况,以验证所设计的核电现场专用吊装伸缩臂的安全性和可靠性[4-6]。
1 新型核电机器人伸缩臂参数确定和受力分析
1.1 参数确定
核电机器人伸缩臂截面形式为六边形截面,共由4节臂套接而成,不同工况情况下的伸缩臂展开情况和起质量也有所不同。本研究主要针对伸缩臂在最大幅度起吊最大质量时的极限工况进行分析,SolidWorks建模后伸缩臂三维模型如图1所示。如果伸缩臂的结构能够通过这种典型的工况校核且满足材料的许用应力要求,可以认为在其他工况下也是安全的[1]。根据总体设计参数表,在极限工况时,伸缩臂的最大力矩M为63 954 N·m,此时伸缩臂全部展开,臂长L为8 360 mm,最大起质量Q为2 900 kg,工作幅度R为2 250 mm,伸缩臂轴线与水平夹角α为69°。另外,基于本设备结构布局和工作环境,做如下假设:吊钩、抓具均计入负载,不再单独计质量;考虑主要在室内工作,忽略风力影响。
图1 伸缩臂全伸状态三维模型
在六边形截面的力学分析中,根据相关截面尺寸参数,分别求得1~4节臂的如下参数:质量,分别为 115、85、115、190 kg;截面积,分别为 3 222、3 925、4 608、5 281 mm4;惯性矩Ix,分别为 1×107、1.9×107、3.1×107、4.7×107mm4;惯性矩Iy,分别为 2×107、3.6×107、5.7×107、8.6×107mm4;断面模 数Wx, 分 别 为 1.47×105、2.21×105、3.06×105、4.05×105mm4;断 面 模 数Wy, 分 别 为 1.67×105、2.64×105、3.72×105、5×105mm4。
1.2 受力分析
由核电机器人的工作原理可知,伸缩臂的臂根部与回转平台连接,可以在垂直面内(变幅平面)自由转动;伸缩臂的基本臂部分与变幅油缸相连,因为变幅油缸的支撑处为一球铰,所以在横向面内(回转平面)对吊臂无任何约束。因此,进行受力分析时,可将变幅平面内的吊臂视为简支梁,将回转平面内的吊臂视为悬臂梁[2]。
变幅平面内,根据受力分析可得

式(1)至式(5)中:S为起升拉力;Qt为垂直载荷;Q为起升质量;Q0为额定起升质量;G0为吊臂自身重力;φ1为起升冲击系数,此处φ1=1.1;φ2为动载系数,此处φ2=1.1;n为起升滑轮组倍率,全伸臂工况下倍率为4;η为起升滑轮组效率,此处为0.985;F为臂架轴向力;Ty为臂架横向力;Mc为臂端力矩;α为伸缩臂与水平面的夹角;β表示钢丝绳与伸缩臂的夹角,β=1°;e1为定滑轮与臂轴线的偏心距,e1=600 mm;e2为导向滑轮与臂轴线的偏心距,e2=130 mm;Ncry为变幅平面临界力;E为弹性模量;Iy为惯性矩;μ1、μ2、μ3均为长度系数,分别为1.74、1.17、1。
代入数据计算得出:F=44 266 N;Ty=8 917 N;Mc=2.14×107N ·mm ;Ncry=1.41×107N。
回转平面内,根据受力分析可得:侧向载荷TX包括重物的偏摆载荷Th以及转化到伸缩臂臂端的风载荷和惯性载荷Tb。若伸缩臂存在副臂工作,则存在臂端力矩MLZ(无副臂工作则为0)。另外,对于回转平面上收到的轴向力,其与在变幅平面内受到的轴向力相同。

式(6)和式(7)中:PH为伸缩臂的惯性力;φ3为惯性系数,该处φ3=1.5;a为加速度,a=0.1 m/s2;m为伸缩臂质量;θ为重物偏摆角,θ=2°;H为起升高度,此处H=8781 mm;Ncrx为回转平面临界力;Ix为惯性矩;μ3为钢丝绳长度系数;C表示风力系数,取C=1.9;L为伸缩臂臂长。
代入数据计算可得:Tx=876 N;Ncrx=2.05×105N。
1.3 许用应力计算
新型核电机器人设备伸缩臂的材料使用高强度HG70钢板,其屈服强度σs=700 MPa,抗拉强度σb=782 MPa,屈强比为σs/σb=0.855,因此,基本许用应力为[σ]=(0.5σs+0.35σb)/n。当强度安全系数n为1.34时,得到基本许用应力值为465 MPa。
2 伸缩臂有限元仿真分析
2.1 有限元模型建立
伸缩臂的三维模型由SolidWorks创建,再将三维模型转换成*.step格式导入Ansys Workebench中打开。
2.2 材料属性定义
通过Engineering Data模块可以定义材料的属性,伸缩臂的结构材料为高强度HG70钢材,密度为8 242.5 g/cm3,泊松比为0.3,弹性模量为205 MPa,抗拉强度为690 MPa,屈服强度为590 MPa。
2.3 网格划分
对模型进行离散化网格划分。单元格的选择直接影响计算结果。若网格类型、尺寸选取不合适,不仅会导致计算结果的精确度会大大降低,计算时间也会延长[4]。对于单元的选取,在此处采用壳单元Shell181进行划分,划分单元后结果为nodes:62 710;elements:63 057。
2.4 边界条件处理
在伸缩臂装配体模型中有大量的接触面,将装配体导入Workbench中系统会将零部件的接触面自动定义为Bonded类型。对于伸缩臂之间的滑块部分,因为每段臂之间不允许接触面的分离且沿着接触面有小的无摩擦移动,所以采用No Separation进行定义[5]。
伸缩臂的位移约束主要在于臂根部和变幅油缸铰接处,所以对于后绞点施加remote displacement约束其3个方向的平动自由度(UX、UY、UZ)和2个方向的转动自由度(Roty、Rotz);将变幅油缸(二力杆构件)进行梁单元处理,使上绞点施加的约束和油缸下绞点与吊臂后绞点相同,施加displacement约束其3个方向(UX、UY、UZ)的平动自由度。
2.5 结果分析
由应力云图分析结果(见图2)可以看出,伸缩臂的最大应力值发生在两节臂之间的滑块接触处,臂1、2、3、4出现的最大应力值分别为424、449、456、478 MPa,伸缩臂总体出现最大应力值为487 MPa。另外,在滑块与各节臂接触处附近的区域有明显的应力集中现象且在臂4处出现的最大应力值478 MPa高于材料的屈服强度465 MPa,因此,可以说明各节臂与滑块接触区域的结构比较薄弱。由于目前起重伸缩臂设计制造基本都是采用滑块连接,可以考虑在设计加工时对滑块的材料、长度、接触面积和支持位置进行改良,从而降低此处应力集中现象[6]。
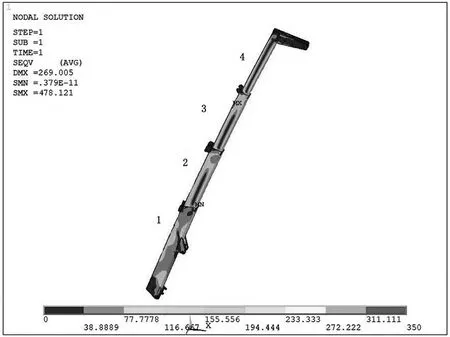
图2 总应力云图
3 结论
通过使用Ansys Workbench对新型核电机器人的伸缩臂极限工况做静力学分析,充分验证了该新型核电机器人承载能力的可靠性和结构的合理性。通过伸缩臂的总应力云图和各节臂的应力云图得出极限工况下伸缩臂的最大应力值出现在臂4与臂3连接处,应力结果为478 MPa,而各节臂的最大应力值均出现在各臂与滑块接触位置,后期可通过改良滑块来降低应力集中现象。另外,根据相关标准,如果结构应力集中区的最大等效应力低于材料本身的屈服强度,则认为该装置的机械设计是安全可靠的,所以该新型核电机器人伸缩臂能够满足设计要求。

