基于残差增强门控循环神经网络的交通流量预测技术研究

金涛斌，卢 宇，徐 岩

（1. 广州大湾区轨道交通产业投资集团有限公司，广东广州 510405；2. 天津大学电气自动化与信息工程学院，天津 300072）

1 引言

随着我国城市化进程的不断加速，交通流量和交通信息量均急剧增加，而当前城市轨道交通运营管理系统功能相对单一，没有充分利用日常运营中长期自然积累的海量数据，缺乏对城市轨道交通运行的长周期自动监控和预测。近年来，国家各相关部门纷纷出台政策，支持智能、高效的城市轨道交通运营管理新技术、新产品、新模式的开发和应用。同时，随着科技的不断发展，计算机运算成本显著降低，基于深度学习的时间序列预测方法已被广泛应用于各个领域。充分利用交通网络的多维度、海量数据，用人工智能的方法来完成交通流量预测工作，可以更加精准地追踪、评价和预测交通流量的动态性变化，对于交通枢纽压力的估计、资源配置、人力调配都具有十分重要的作用。本文研究高性能深度学习交通流量预测算法，自动捕捉输入数据的时间相关性和依赖性，根据当前状态和历史数据对大规模交通网络中各个枢纽的交通流量进行预测，实现交通枢纽客流量的智能化、高效率、高准确率预测，助力提升城市轨道交通运营管理水平。由于本文算法可应用于各种类型交通（包括：城市轨道交通、公路交通等），故后文统一论述为“交通流量预测”“交通网络”“交通枢纽”。

2 国内外研究现状

交通网络所具有的拓扑特点和极具时效性的时域特征导致在网络中各个交通枢纽之间的相互关联具有很强的动态变化性。从时间特点而言，交通流量具有极强的周期性和非线性时域变化的特点，时间相关性也更复杂。在一周的同一天或同一天的同一时段，同一地点的交通流量通常相似，而前一时段的交通流量也会对后续时段产生很大影响。这使得交通流量预测长期以来一直是一项具有挑战性的任务[1]。

近年来，人们对高性能智能交通流量预测系统的开发越来越感兴趣。交通流量预测的早期研究通常使用传统的理论统计方法，如历史平均值方法（HA）[2]，自回归综合移动平均方法（ARIMA）[3]和向量自回归方法（VAR）[4]。其中，ARIMA是应用最广泛的时间序列模型，为了提高模型的预测精度，引入了不同的变量加以改进，如周期ARIMA[5]等。Van Hinsbergen等人通过最小化最优解的方差，使用卡尔曼滤波器完成交通预测任务[6]。虽然传统的统计方法相对简单且便于计算，但它们均需满足基于时间序列的平稳性假设[7]，而真实交通流量数据通常并不能严格满足平稳性要求。

随着深度学习在语音识别和图像处理等领域的逐渐成熟，越来越多的研究人员将深度学习应用于时空数据预测[8]。卷积神经网络（CNN）已被广泛用于捕捉欧几里得空间中的时空相关性[9]。Huang等人提出扩散卷积递归神经网络（DCRNN）模型，将图卷积集成到编码器-解码器结构的门控循环单元中[10]。于德新等人将门控循环单元（GRU）与递归神经网络（RNN）结合，对交叉路口的交通流量进行预测[11]。凤少伟等人将K均值方法与GRU结合进行交通流量预测，也取得较好效果[12]。Zhao等人将长短时记忆网络（LSTM）和全连接网络（FCN）集成，提出LSTM-FC网络来提取时间序列数据的相关性[13]。Fang等人将卡尔曼滤波和LSTM结合用于短期交通流量预测[14]。

综上所述，虽然这些方法基本实现了对时序数据的建模和分析，在交通流量预测方面取得了惊人的进展，但捕获长期时间依赖性的能力有限，所得的预测结果仍然有较大的提高空间。

3 算法描述

3.1 门控循环单元

Cho等人在LSTM的基础上提出了结构更加紧凑的GRU，其结构如图1所示[15]。

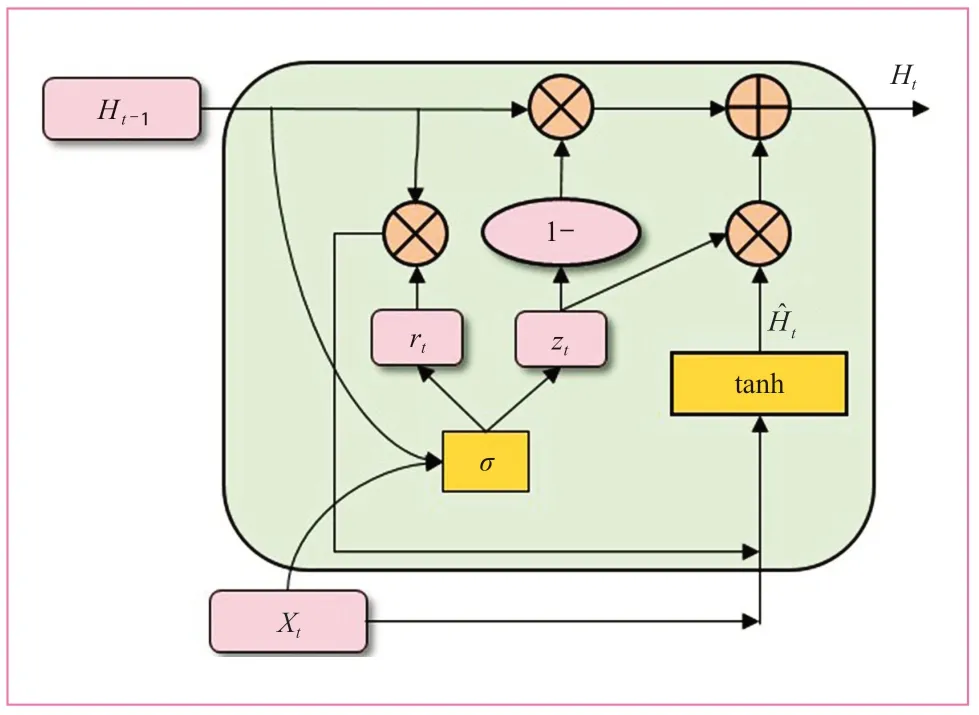
图1 GRU结构示意图

GRU将LSTM中的输入门（input gate）和遗忘门（forgetting gate）整合成为更新门（update gate），用来控制过去时刻记忆信息参与当前时刻信息计算的数据量，以及前一时间步的信息和当前时间步的信息将被继续传递到未来时间步的数据量，其计算公式如下：

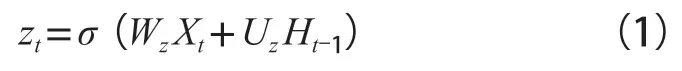
式（1）中，zt为t时间步GRU单元的更新门输出；σ为非线性激活函数，其输出为（0，1）之间的数值，可以直接作为门控信号；Wz和Uz为更新门中可训练的模型参数；Xt为t时间步的输入；Ht-1为前一时刻即t-1时间步的隐藏层状态。

GRU的另一个门为重置门（reset gate），其计算方法与更新门类似：

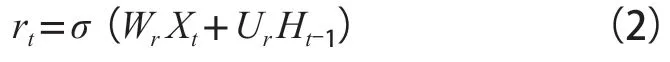
式（2）中，rt为t时间步GRU单元的重置门输出；Wr和Ur为重置门中可训练的模型参数。

得到2个门控信号后，首先根据当前时刻输入、前一时刻隐藏层状态 以及重置门控信号 ，计算得到：

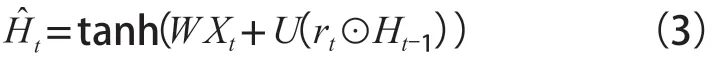
最终得到当前t时刻的隐藏层状态Ht：

3.2 残差连接

深度神经网络在训练过程中容易过度拟合，最终会损害预测精度。为了解决这一潜在风险，文献[16]提出在深度神经网络的某些层次之间增加额外的连接结构，如图2所示。加入残差连接后，其映射函数H（x）的计算公式如下：

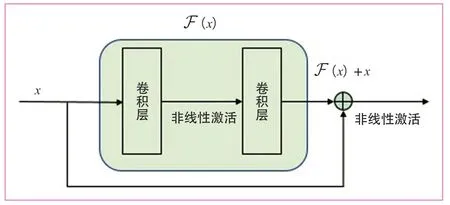
图2 残差连接示意图

式（5）中，x为当前残差模块的输入特征；（·）为2 ～3层卷积、激活等操作。残差连接既没有增加额外的参数，也没有增加计算复杂度，但有助于网络模型学习到更多的信息，以进一步提高模型的准确性。

3.3 残差增强的门控循环网络

与LSTM类似，GRU被用于解决反向传播中的长时间建模和梯度消失等问题，它比LSTM具有更简单的结构和更少的参数。但是，GRU仍然基于输入数据的顺序进行迭代处理，当建模长时间序列时，预测效果会衰减。

残差连接用于解决深度神经网络在训练过程中出现的过拟合问题。在GRU中添加残差结构可以在一定程度上缓解长时间建模的衰减效应。传统残差结构一般是在递归循环单元的输入和输出之间添加连接。本文算法选择在迭代之间添加线性连接以构建残差增强门控递归单元（R-GRU），并将I个单元（对应于I个历史时间步长）级联起来，以形成残差增强门控递归层，其结构如图3所示。R-GRU结构可使信息能够从一个单元直接传播到另一个单元，这有助于网络学习更多信息并进一步提高模型的准确性。

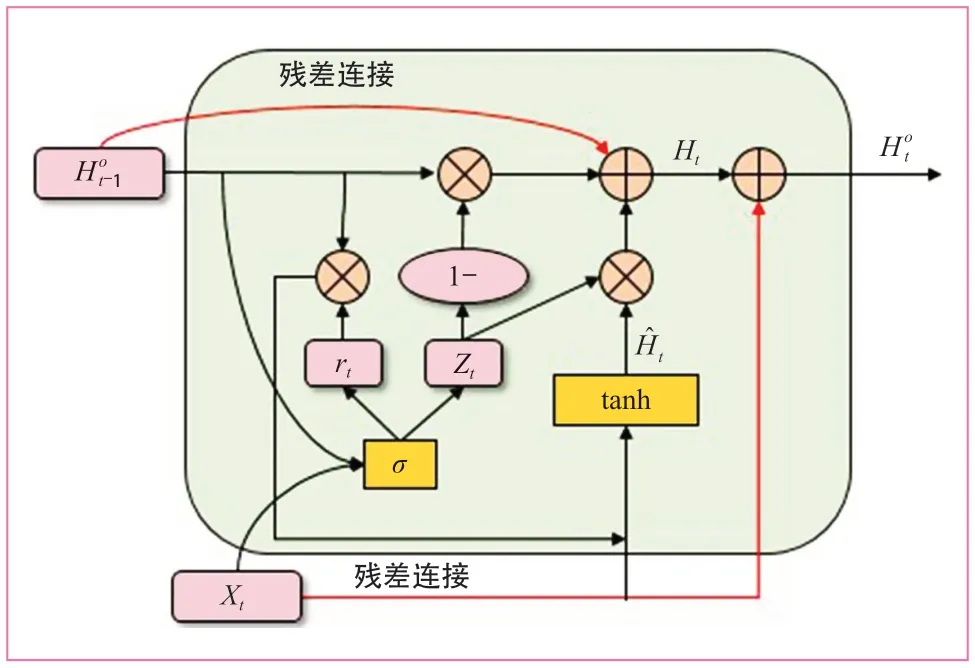
图3 R-GRU结构示意图

添加残差连接后，R-GRU的前馈传播递归地进行为：

式（6）～（10）中，为R-GRU单元在时间步t的输出；αx和αh为超参数；Wh和Wox为可训练的模型参数。

4 实验与分析

为测试本文算法的性能，对4个公开的公路交通数据集PeMS03、PeMS04、PeMS07和PeMS08进行了实验[17]，数据集的统计信息如表1所示。

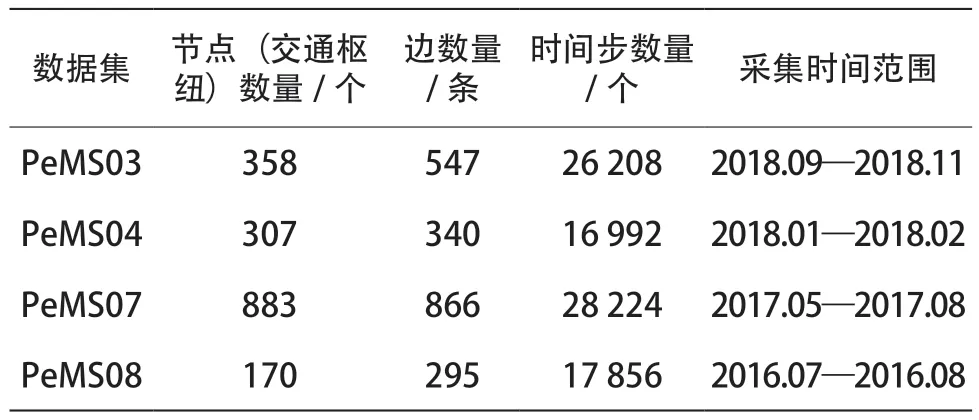
表1 实验所用数据集信息

所有实验均在1台配有3.6 GHz的Intel（R）Core i7-9700k处理器、1块GeForce GTX 3080Ti GPU的电脑上完成。深度学习网络模型基于Pytorch框架实现。实验采用了3种评估指标：平均绝对误差（MAE）、均方根误差（RMSE）和平均绝对百分比误差（MAPE）。上述指标的计算公式为：

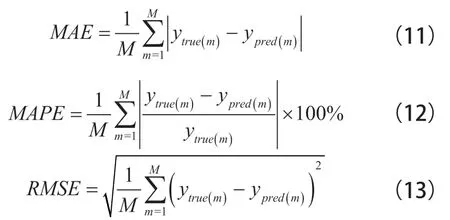
式（11）～式（13）中，ytrue（m）为第m个样本的真实值；ypred（m）为第m个样本的预测值，M为样本数量。

实验中使用数据集中前1 h的历史数据预测未来1 h的交通状况。本文算法与其他算法的预测性能比较如表2所示。可以看出，由于交通流预测不是一个简单的时间序列线性分析问题，而是一个复杂的时空预测问题，所以传统的统计模型（HA[2]、ARIMA[3]和VAR[4]）表现不佳。与基于深度学习的方法（LSTM-FC[13]和DCRNN[10]）相比，本文所提出的模型表现出具有竞争力的性能，所有指标均优于上述算法。实验中使用的4个数据集在节点数和时间跨度上有很大差异，本文算法在所有这些数据集上都保持了较高的预测精度，这意味着本文算法能够胜任不同交通网络的预测任务。

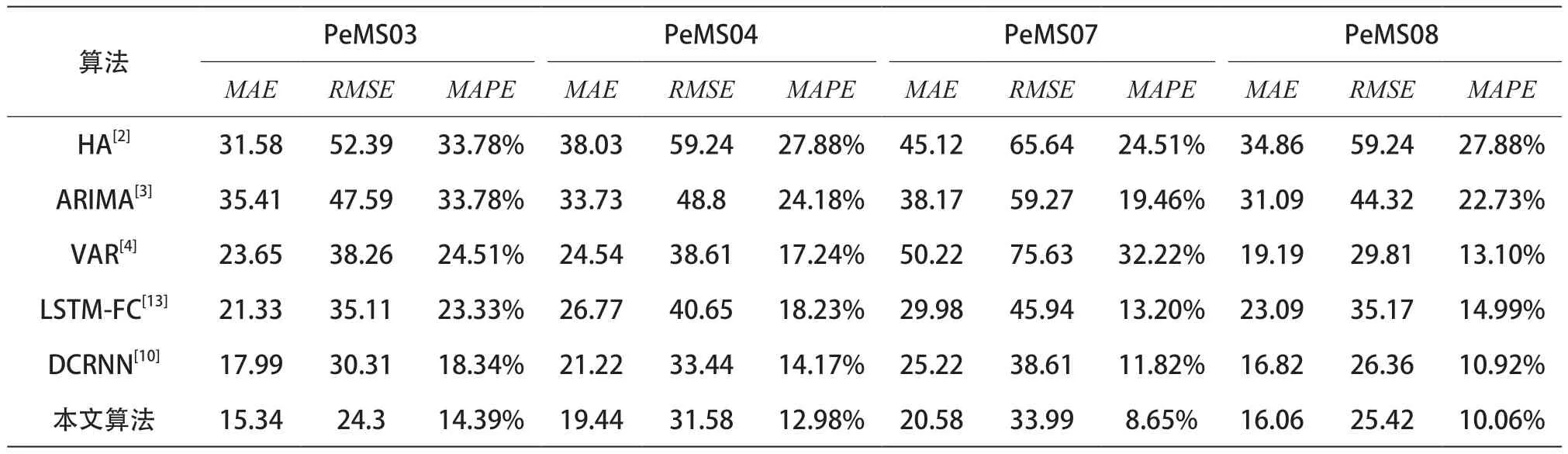
表2 本文算法与其他算法的预测性能比较

为更加直观的观察算法预测性能，在PeMS04中随机选择2个节点（节点1和节点99），将流量真实值与本文算法预测值进行可视化展示，如图4所示。可以看到，真实值曲线非常不规则，在某些时间点上波动很大，同时，不同节点的交通流变化模式也非常不同。而本文模型能够准确地捕捉并拟合不同节点中交通流量剧烈变化时的不同规律，尤其是在显著变化的峰值或波谷时对流量变化较敏感，预测结果接近实际值。

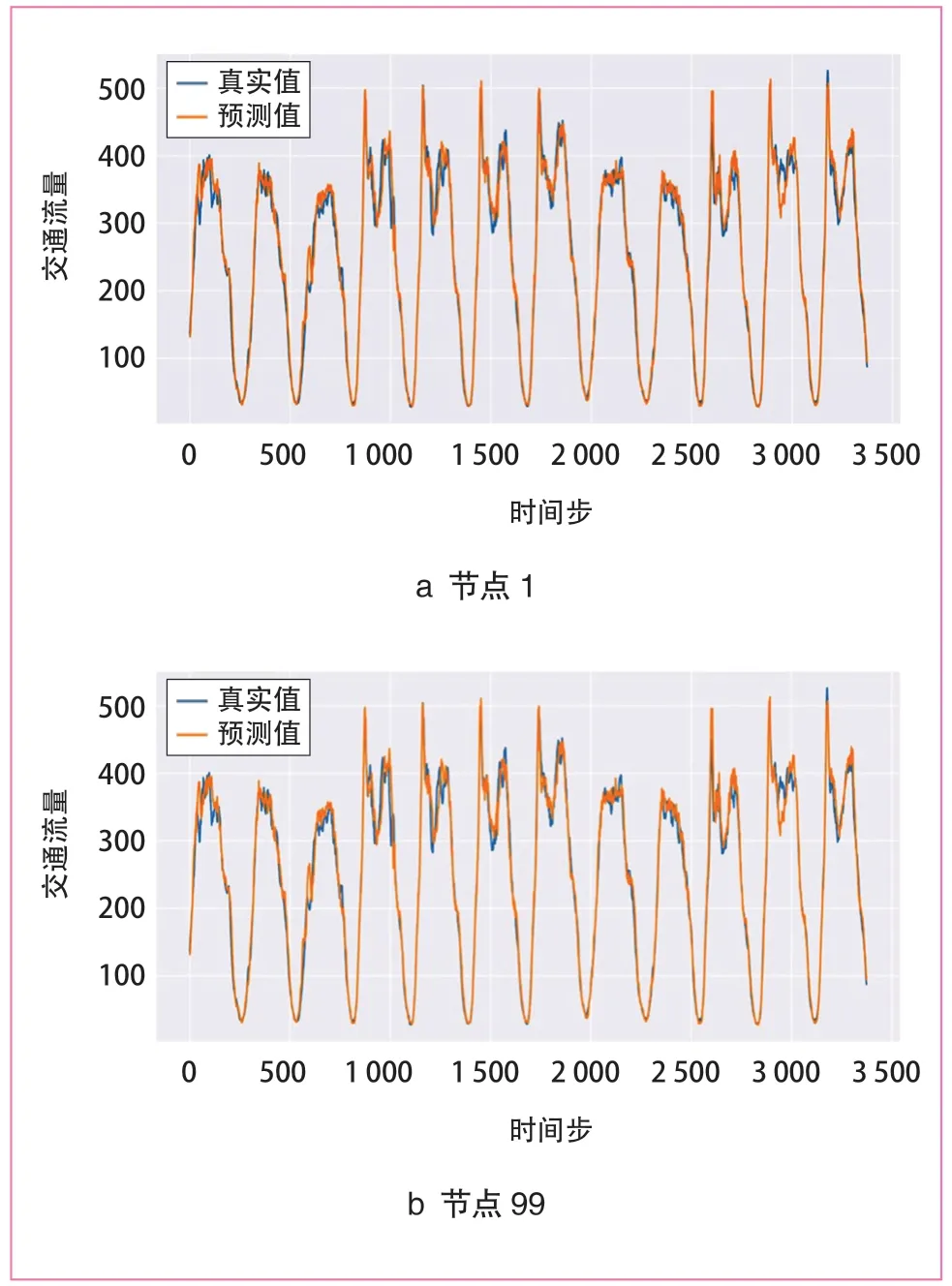
图4 PeMS04中节点1和节点99的真实值与预测值比较

5 结论

本文针对大规模交通网络的流量预测问题，改进了门控循环网络结构，通过增加残差连接，提出基于残差增强门控循环网络的交通流量预测算法来预测未来时间步长的交通状况。在4个公开交通数据集上的实验表明，本文算法在预测精度方面具有显著竞争力，能够同时捕捉不同节点的流量变化规律，即使在流量变化非常不规则且变化较大的时间步，仍然能够给出较准确的预测结果。

高性能交通流量预测算法能够及时有效地获取未来某段时间内的交通信息，及时做出合理的人员安排和引流部署，节约处理交通拥堵问题的经济开支，可缓解很多交通预测领域的现实问题，具有较高的研究价值和应用价值。未来我们的研究将侧重于同时考虑交通网络的时间-空间变化特征，同时将影响交通流量的天气、节假日信息和交通事故等因素纳入模型，以进一步提高预测精度。