基于Voronoi网格研究ZnO压敏电阻微观参数对其电气性能的影响
程宽,赵洪峰
(新疆大学 电气工程学院 电力系统及大型发电设备安全控制和仿真国家重点实验室风光储分室,新疆 乌鲁木齐 830046)
ZnO压敏电阻的电气特性由ZnO晶粒(欧姆元件)与晶界(非线性元件)串、并联所构成的复杂网络决定[1-3]。ZnO晶粒的尺寸、几何形状和拓扑结构以及晶界层的性能和电气特性分布都对ZnO压敏电阻的宏观电气特性有明显影响[3]。然而,目前对于ZnO压敏电阻微观结构的性能和分布,与形成宏观ZnO压敏电阻的随机网络整体行为之间的关系只有粗略的认识。高性能ZnO压敏电阻的研发仍旧以大量的尝试性试验研究为主,不仅浪费时间,而且效果不明显。高性能ZnO压敏电阻的研发非常需要有针对性的理论指导以及材料的设计方法,从而避免许多尝试性的试验,缩短研发周期,节约研发成本。通过模拟分析ZnO压敏电阻的实际微观结构和电气特性,可以有效分析不同掺杂剂和烧结工艺对晶粒尺寸、泄漏电流、非线性系数等电气性能参数的影响[4],有助于揭示其微观结构与宏观特性之间的联系[5],对于高性能直流ZnO压敏电阻的研发具有重要的指导意义。
研究学者们通过微接触法测量了ZnO压敏电阻中单个晶界的电流-电压(I-U)特性,发现并非所有的晶界都表现出优异的非线性I-U特性[6]。早期的研究者将晶界简单地分为“好”和“坏”2种:“好”意味着晶界具有良好的非线性I-U特性;“坏”则表示非线性不佳,甚至表现出线性特性[7-8]。上述晶界分类包含了描述压敏电阻晶界模型的基本物理特征,编程也相对简单,但过于理想化,不能反映晶界的真实复杂情况。Bartkowiak和Mahan首次提出一个电路模型,并使用Voronoi网格(一组由连接2个邻点直线的垂直平分线组成的连续多边形组成的网络)描述ZnO压敏电阻的实际微观结构,其中晶粒和晶界随机分布[9]。Bartkowiak等人在前人的研究基础上,在仿真模型中对晶界进行了进一步的划分,将其分为高非线性的“好”晶界、非线性差的“不良”晶界、低电阻率线性欧姆晶界[10-11]。上述模型中的晶界分类均基于以前的经验公式描述压敏电阻的电气特性,而不是基于实际的晶界传导机理。这意味着上述模型所呈现的电气特性都是现象,而不是物理描述。Long等人考虑了晶界的详细物理描述,特别是晶界的电容特性,这使得模拟ZnO压敏电阻的交流和冲击性能成为可能[12]。在此之后,研究学者基于真实的ZnO压敏电阻的晶界导电模型及微观参数,提出了新的计算模型和算法,利用Voronoi网格模拟ZnO压敏电阻在交流和冲击下的电气特性[12]。
研究工作者们利用Voronoi网格主要模拟了晶粒尺寸、气孔率、尖晶石等变化对ZnO压敏电阻电气性能的影响[5,13]。然而,却少有学者基于真实的ZnO压敏电阻的晶界导电模型,利用Voronoi网格模拟ZnO压敏电阻在施加直流电压作用下,其微观参数的变化对宏观电气性能的影响。ZnO压敏电阻在老化过程中,变化的微观参数主要是施主浓度Nd和表面态密度Ni等,这些微观参数的变化直接影响ZnO压敏电阻的电气特性[14]。因此,可以将ZnO压敏电阻的微观参数与电气特性之间的复杂关系转化为多变量和多目标的优化问题。本文基于真实的晶界导电模型和算法,模拟研究ZnO压敏电阻微观参数变化时其电气特性宏观参数的变化规律。这有助于理解其微观参数与电气特性的复杂关系,对直流ZnO压敏电阻的掺杂改善研究具有指导意义。
1 ZnO压敏电阻的仿真模型
1.1 晶界I-U特性的仿真模型
相邻2个ZnO晶粒之间的晶界是压敏电阻非欧姆特性的起源[13-14],ZnO压敏电阻的电气特性是众多晶粒和晶界串、并联后的综合效应。晶界的I-U特性与ZnO压敏电阻整体的I-U特性相似,模拟ZnO压敏电阻微观结构与整体电气特性之间复杂联系的关键,在于分析晶界的计算模型和电气特性。Bartkowiak等以往的模拟都是基于ZnO压敏电阻单晶界的I-U特性模型,并利用该模型分析其电气性能和热特性[14]。然而上述模拟却存在着严重缺陷:使用以往近似的经验公式而不是晶界的实际传导机理来描述晶界的电气性能。
多年来,研究学者们提出了多种理论以解释晶界层的传导机理[14]。截至目前,由Pike、Blatter等人提出的基于电荷填充表面态导致肖特基势垒高度φb降低的导电机理,得到越来越多研究者的支持,能够解释绝大多数实验现象[15]。在理想情况下,通过热电子发射描述电流跨晶界输运的完整I-U特性可以更好地提高模拟精度;然而,ZnO压敏电阻在外施电压的作用下,其内部的电流除了主要通过双肖特基势垒所形成的主流路径外,还会有较小的泄漏电流流经厚度较大且具有高阻特性的晶间相。旁路路径的存在必然会对压敏电阻的电气特性产生相应的影响。为此,清华大学的胡军等基于Eda介绍的晶界旁路效应模型重新划分晶界层,将晶界层分成3种类型,如图1所示[5]。该模型是目前被研究者公认的较为完善的仿真模型,能够更准确地反映晶界层的真实情况[5,11]。

图1 单个晶界层的分区模型Fig.1 Zoning model of single grain boundary layer
I型(无晶间层):在2个晶粒之间的接触区域无晶间层。由于晶粒电阻率较小,相比于较厚晶间层的阻抗和较薄晶间层区的非线性阻抗,可以完全忽略该区域阻抗,因此该区域很少被关注及研究。
II型(薄的晶间层):富Bi2O3的晶间层在接近晶粒的接触点时变得非常薄,其厚度约为10~1 000 Å,因此很难通过电子显微镜观察到晶间层的存在。该区域位于相邻的ZnO晶粒的紧密接触位置,非线性的双肖特基势垒在此区域形成,它是压敏电阻非线性的起源。
III型(较厚的晶间层):具有较大厚度的富Bi2O3晶间层存在于相邻2个晶粒的边缘区域,其厚度约为0.1~1 μm。在液相辅助烧结的冷却阶段,融入液相中的大量添加剂在此区域发生偏析,导致该区域电阻率较高,然而在此区域却无肖特基势垒形成。
Tao M等对单个晶界层的电气特性进行了大量的研究,发现其各项参数都近似正态分布[16]。因此,本课题组在新的晶界层分区模型中,将I型、II型、III型这3个区域所对应的晶界面积与晶界的总面积之比分别定义为AI、AII、AIII,并使用正态分布函数进行模拟。
参数x(AI、AII、AIII)的正态分布模型为:
(1)

(2)
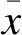
本文主要研究ZnO压敏电阻在直流电压下,其宏观电气性能与微观结构的联系。在此情况下,可以忽略晶界电容的存在,仅考虑晶界的实际传导机理。因此,本文依据电荷填充表面态致使肖特基的势垒高度φb降低的导电机理,建立单个晶界的仿真模型,如图2(a)所示,其中RIL、RDB分别为晶粒之间III型区域的电阻、II型区域的非线性电阻,RA1和RA2、RB1和RB2、RC1和RC2分别为III型区域、II型区域、I型区域两侧晶粒的部分电阻。该电路模型可以从Blatter和Greuter提出的实际传导机制推论得出模型参数[14]。RDB可根据施加在晶界上的电压U与通过势垒面积为S的电流密度J之比计算获得[4-5]:
(3)

为了方便计算晶界的状态方程,本文通过合并一些电阻元件对图2(a)所示的等效电路进行优化处理,图2(b)为优化后的单个晶界层的等效电路,其中RB、YAC、YDB分别为等效电阻和等效导纳。
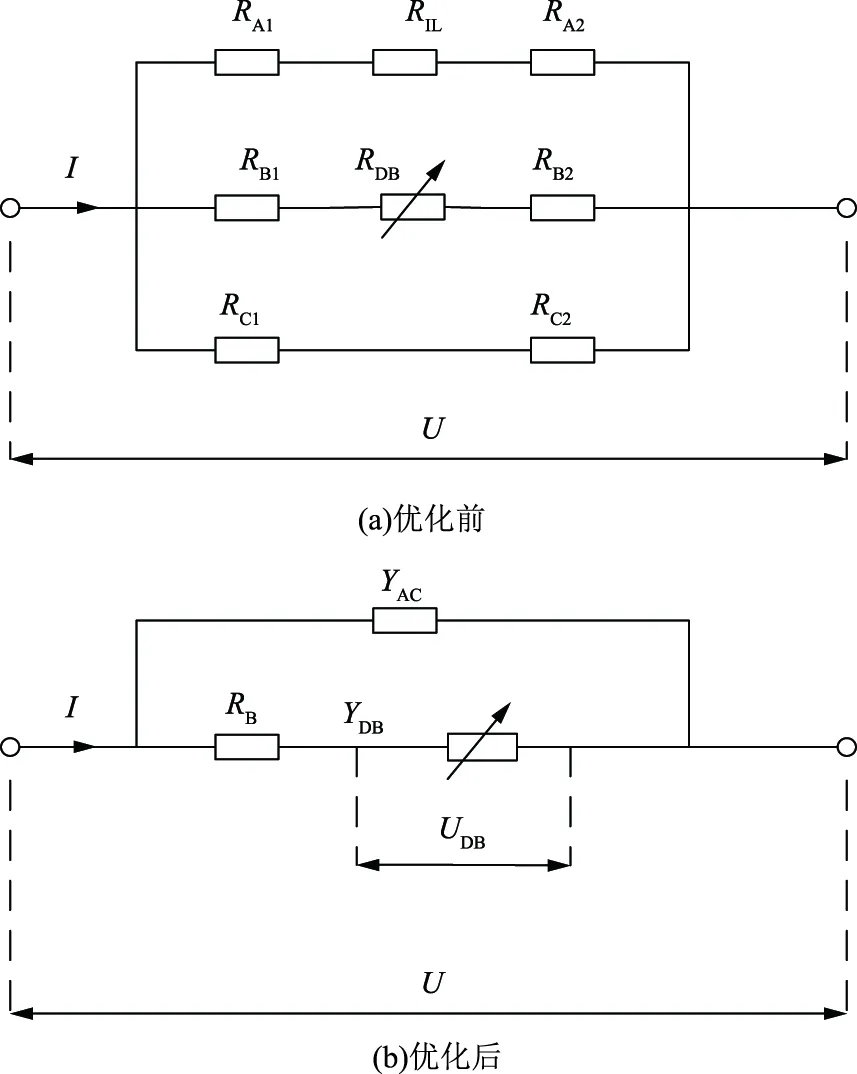
图2 单个晶界层的等效电路Fig.2 Equivalent circuit of single grain boundary layer
(4)
1.2 基于Voronoi网格的二维仿真模型
图3、图4分别为ZnO压敏电阻实际的扫描电子显微镜(scanning electron microscope,SEM)图像和Voronoi网格的拓扑结构图。
由图3可知,压敏电阻的微观结构由大小不一的晶粒和晶界构成,类似填充蜂窝状。由Voronoi网格模拟生成的ZnO压敏电阻的几何形状和拓扑结构(图4),与实际ZnO压敏电阻样品的微观结构非常相似。使用Voronoi网格对ZnO压敏电阻复杂的微观结构进行建模,可以简单形象地模拟出ZnO晶粒在高温烧结过程中随机生长的过程。

图3 ZnO压敏电阻样品实际微观结构的SEMFig.3 SEM image of actual microstructure of the sample

图4 种子随机分布的Voronoi网格拓扑结构Fig.4 Topology of Voronoi grid with random seed distribution
Voronoi网格由随机生成的多边形组成,并且相邻多边形之间没有间隙,这些多边形覆盖了一个空间区域。Voronoi网格是通过在规定的区域内生成n个随机种子来建立的,其生成算法如下:首先确定Voronoi网格生成区域,然后定义种子点的阵列,该阵列能够以某种方式关联或者完全随机地生成种子。Voronoi网格通过连接相邻种子直线的垂直平分线相交而形成[7],该结构由完美堆积在一起的平面多面体组成,任何多边形与其相邻的多边形之间的形状都是相互依赖的。生成种子的分布决定了多边形的几何形状,使用不同初始分布时,可以生成不同几何形状的多边形。如果种子点以相同的间隙(间隙H=1)排列,则通过在半径为r的圆内围绕种子的原始位置移动各个种子点来引入无序,其中r以三角形网格中最近邻居之间的距离为单位来定义,称为无序度[7-8]。然后施加周期性的边界条件,使单元总数保持不变。可以通过改变无序度来调节Voronoi网格的不均匀性[10]。
从物理上讲,Voronoi网格可以被解释为一个二维的生长过程,该过程同时在所有成核种子处开始,并以恒定的均匀速率在平面中进行,直到2个接近的生长前沿彼此到达时终止[11]。因此,Voronoi网格的几何形状和拓扑结构与晶粒的生长非常相似。基于上述微观结构和晶界模型,ZnO压敏电阻样品的二维Voronoi网格的等效电路如图5所示(其中Us为电源电压,Rij为晶界电阻),Voronoi多边形的每条边线都应该被晶界的等效电路支路﹝如图2(b)所示﹞所代替。Voronoi网格中的每个多边形代表1个晶粒,而彼此相邻的多边形共享的每条边则对应1个晶界。使用Voronoi网格可以有效地模拟ZnO压敏电阻的无序结构,并且通过改变无序度来模拟ZnO压敏电阻的不均匀性[8,11]。然后,根据Voronoi网格模型推导出晶粒间的电气关系。如果2个多边形之间存在共享边,则使用非线性电阻来模拟它们之间的电气关系。在ZnO压敏电阻高温烧结过程中会产生尖晶石和气孔,它们的存在对ZnO压敏电阻的电气性能具有非常明显的影响。为了真实模拟ZnO压敏电阻内部的微观结构,本文根据气孔和尖晶石的占比随机指定一些多边形并调整其边界参数,将其调整为绝缘状态和高阻状态,以此来模拟ZnO压敏电阻内部的气孔和尖晶石。
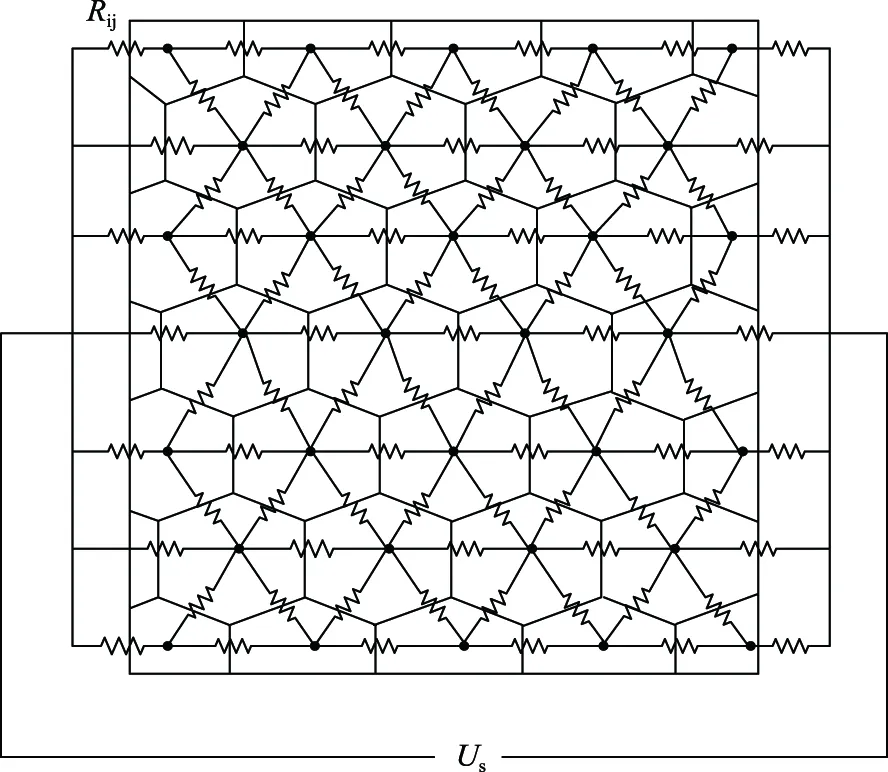
图5 ZnO压敏电阻的等效电路Fig.5 Equivalent circuit of ZnO varistor
2 求解等效电路的算法
在测量压敏电阻电流密度-电压梯度(J-E)特性曲线时,外施在其两端的电压是逐步增加的。在等效电路的求解过程中,本文采取类似的策略逐步增加外施电压,晶界的动态电阻率随外施电压的变化而变化,需对其进行离散和分段线性处理以简化计算。根据图5所示的ZnO压敏电阻的非线性阻抗网络,基于基尔霍夫定律可建立一组非线性方程[4]:
(5)
式中:I、U分别为支路电流、电压b维向量(b为电路支路的数量);UN为节点电压的(n-1)维向量(n为电路节点的数量),其最后一个元素等于外部施加的电压Us;A为描述所有节点和分支关系的(n-1)×b维矩阵;f为各支路(不包括外加电压源支路)电流和电压的函数;Ij、Uj分别为支路j的电流、电压。
非线性方程组(5)相比于以前的简单经验公式复杂得多,传统的牛顿迭代法已经无法满足其求解问题。因此,本文采用如图6所示的快速分段线性方法求解,其中U(L)和I(L)分别为等效电路中各节点和各支路第L步迭代(以上标(L)表示,下同)的电压和电流。该方法无需求解每一步外施电压下各个节点及支路的电流、电压,只需根据前一步的求解结果计算电压变量对各个节点及支路的影响,从而获得此刻外施电压下的相关数据[5]。在计算求解过程中,电压变量的设定一般较小,可以使用小信号分析法对ZnO压敏电阻的非线性等效电路进行线性化处理,该处理方法能够明显降低计算过程,缩短计算时间。

图6 求解非线性等效电路的快速分段线性方法Fig.6 Fast piecewise linear method for solving nonlinear equivalent circuit
将第L+1步与第L步非线性方程组相减可得:
(6)

(7)

令
(8)
整理可得:
(9)
图2(b)所对应的晶界等效电路的状态方程可以表示为:
(10)
当外部施加的电压由L步增到L+1步时:
(11)
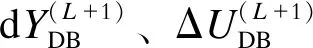
由式(11)的第1个方程可得
(12)
(13)
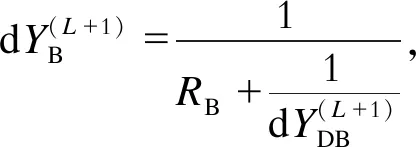
(14)

ΔI(L+1)=dY(L+1)ΔU(L+1).
(15)
因此,在施加直流电压的情况下,式(6)可转化为:
(16)
对于直流电源,根据式(16)可以快速求解ZnO压敏电阻原始非线性等效电路的响应。
3 ZnO压敏电阻电气性能的仿真与验证
3.1 仿真模型与输入参数的选取
本文基于ZnO压敏电阻晶界层的实际导电机理和新的分区模型,使用其本征的物理参数建立仿真模型,考虑直流电压下ZnO压敏电阻的微观结构、晶界特性与宏观电气参数之间的复杂关系,进行仿真模拟分析。相关研究已经证明,使用30×60个ZnO晶粒所构成的小规模尺寸仿真模型与60×60个ZnO晶粒所构成的仿真模型在计算结果差异较小[5]。使用小规模尺寸仿真模型,能够有效地与工厂生产的ZnO压敏电阻样品的实测数据保持一致,并且仿真结果的误差小于5%,在可接受的范围内[5]。因此,本文将30×60个ZnO晶粒所构成的小规模尺寸仿真模型作为后续仿真模拟的基本尺度。
为了真实地反映ZnO压敏电阻实际微观结构与电气性能的关系,本文仿真模型中所输入的物理参数部分选自ZnO压敏电阻样品实测数据。ZnO压敏电阻的平均晶粒尺寸d和无序度σ等参数,可以通过ZnO压敏电阻微观结构的SEM图像测量和统计获得,d和σ的计算公式为[14]:
(17)
(18)
式中:l为SEM上的随机线长度;M为SEM的放大倍数;N为线所截取晶界的数量;di为第i个ZnO晶粒的实际尺寸;s为实际测量晶粒的总数。为了减少误差,在每个ZnO压敏电阻的SEM图像中进行了多次测量并求取平均值。
3.2 仿真模型与输入参数的选取
为了检验本文选用的仿真模型和输入参数的准确性,对实际ZnO压敏电阻的J-E特性进行仿真,并使用数字源表(Keithley 2410)测量该实际ZnO压敏电阻在预击穿区域的J-E特性。ZnO压敏电阻的仿真结果与实际测量结果的对比如图7所示,可以看出仿真曲线与实测曲线非常吻合。
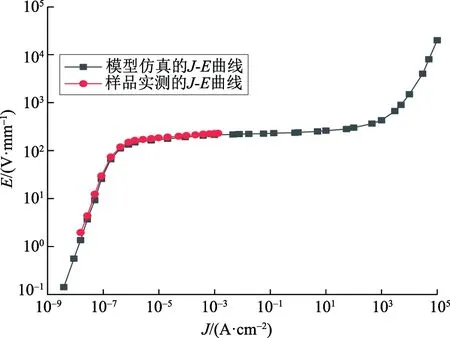
图7 ZnO压敏电阻J-E特性曲线Fig.7 J-E characteristic curves of ZnO varistor
4 不同微观参数对ZnO压敏电阻电气特性的影响分析
对ZnO压敏电阻微观结构和电学特性的仿真模拟,可以分析ZnO压敏电阻的d、ρ、Nd、Ni等微观参数的变化对整体电学特性的影响,以便理解压敏电阻微观结构与宏观电气性能之间的复杂关系。为了避免其他因素的干扰,本文采用单一变量原则,即在多变量仿真过程中改变指定参数,同时维持其他参数不变。
4.1 d对ZnO压敏电阻电气特性的影响
d的变化对ZnO压敏电阻样品J-E特性曲线的影响如图8所示,对样品电气性能的影响见表1,其中,E1mA为1 mA直流电流密度下的电压梯度,α为非线性系数,JL为泄漏电流密度,K为残压比。

图8 d的变化对样品J-E特性曲线的影响Fig.8 Effect of changes of d on J-E characteristic curves of sample

表1 d的变化对样品电气性能的影响Tab.1 Effect of d changes on electrical properties of sample
由表1可知:随着d的增大,E1mA明显减小,K则逐渐增大;d的变化对JL、α的影响较小。E1mA的计算公式为[3]:
(19)
式中:Ugb为单个晶界的击穿电压;Ng为单位长度内晶界层的数量。由式(19)可知,ZnO压敏电阻的E1mA取决于单位厚度内晶界层的数量和单个晶界的击穿电压。ZnO压敏电阻内部单个晶界的击穿电压基本不变,约为3 V[4,17]。d的增大将导致ZnO压敏电阻单位厚度内的晶界层数目减少,这是d增大致使ZnO压敏电阻的E1mA减小的根本原因。ZnO压敏电阻的残压比K可由其在上升区域大电流密度下的电压梯度E与E1mA相比计算获得,即[4]
(20)
由式(20)可知,降低K值可以通过以下2种途径实现:①降低ZnO压敏电阻在上升区域的E;②提高ZnO压敏电阻在预击穿区域的E1mA。ZnO压敏电阻的K随着d的增大而逐渐增大,这是由于d的变化对ZnO压敏电阻在预击穿区域的E1mA有明显影响,E1mA的降低将致使K增大。因而,可以通过抑制晶粒生长来减小d值,从而提高ZnO压敏电阻的E1mA,降低K值,改善ZnO压敏电阻的电气性能。
4.2 ρ对ZnO压敏电阻电气特性的影响
ρ是ZnO压敏电阻的重要微观参数,对ZnO压敏电阻的电气性能有非常明显的影响。ρ的变化对ZnO压敏电阻样品J-E特性曲线的影响如图9所示,对样品电气性能的影响见表2。由表2可知,ρ的变化对E1mA、JL、α的影响相对较小,但对K值的影响非常明显。

图9 ρ的变化对样品J-E特性曲线的影响Fig.9 Effect of changes of ρ on J-E characteristic curve of sample

表2 ρ的变化对样品电气特性的影响Tab.2 Effect of ρ changes on electrical properties of sample
4.3 Nd对ZnO压敏电阻电气特性的影响
Nd的变化对ZnO压敏电阻样品J-E特性曲线的影响如图10所示,对样品电气性能的影响见表3。随着Nd的增大,E1mA和α明显降低,而JL则表现出与之相反的变化趋势,这些参数的变化意味着ZnO压敏电阻电气性能的下降。Nd的减小能够明显提高ZnO压敏电阻在预击穿区域的电气性能,而对上升区域的影响则相对较小。在上升区域的E基本不变的情况下,可以通过增大E1mA来降低K值。Nd对K值的影响,是通过改变E1mA来实现的。因此,可以通过抑制Nd的增大来降低K,增大E1mA。

图10 Nd的变化对样品J-E特性曲线的影响Fig.10 Effect of changes of Nd on J-E characteristic curve of sample
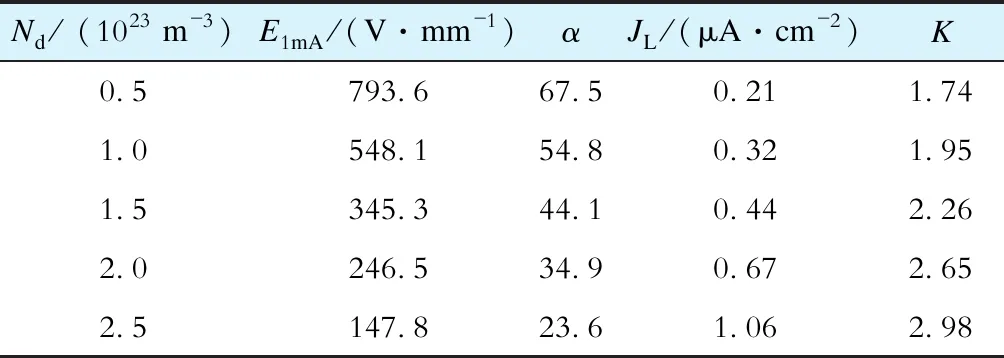
表3 Nd的变化对样品电气性能的影响Tab.3 Effect of Nd changes on electrical properties of sample
4.4 晶粒边界参数对ZnO压敏电阻电气性能的影响
在第2章中,本文将整个晶界分为Ⅰ型、Ⅱ型、Ⅲ型3种类型,这3种类型所对应的面积在整个晶界中的占比不同,晶界将表现出不同的电气性能。晶界电气性能的好坏严重影响着ZnO压敏电阻的宏观电气性能。为此,本文对晶粒边界参数对其电气性能的影响进行研究。如图1所示,在直接接触区域,2个ZnO晶粒之间彼此接触,无晶间层的存在。通过改变直接接触区域的面积在整个晶界中的占比AI,来研究其对ZnO压敏电阻的E1mA、JL、α、K的影响。实验结果如图11和表4所示,AI的大小对压敏电阻的α、JL有明显影响,而对K值的影响则微乎其微。
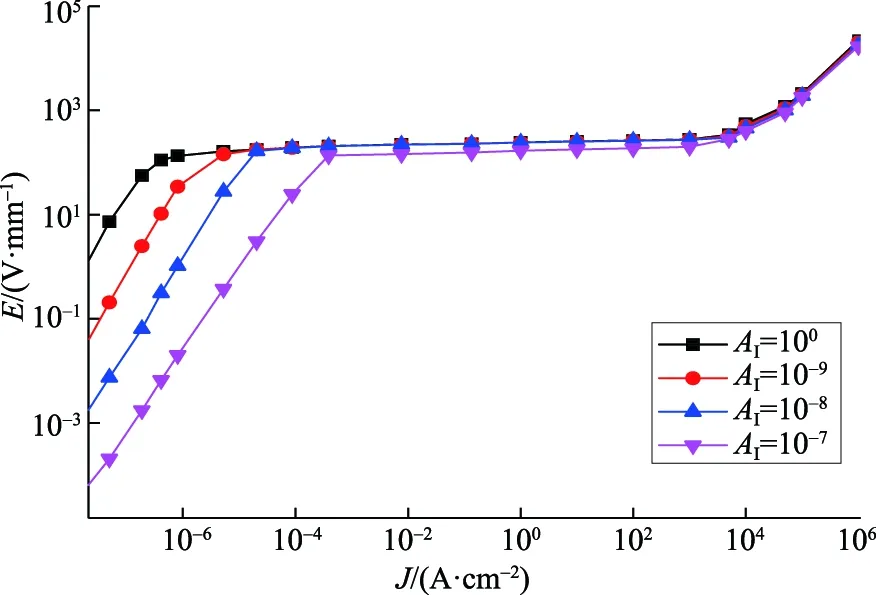
图11 AI的变化对样品J-E特性曲线的影响Fig.11 Effect of changes of AI on J-E characteristic curve of sample
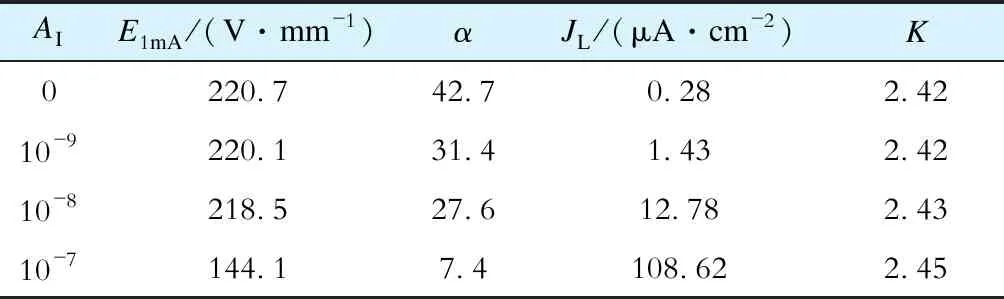
表4 AI的变化对样品电气性能的影响Tab.4 Effect of AI changes on electrical properties of sample
α是极其重要的电气参数,其值越大意味着压敏电阻在其非线性区域的J-E特性曲线越平坦,ZnO压敏电阻保护性能越好[17]。非线性区域的J-E特性曲线可以延伸超过6个或7个数量级的电流,即使JL急剧增大,ZnO压敏电阻的电压也仅有小幅提升[4]。这能够有效抑制电力系统中的过电压。ZnO压敏电阻的α随着AI的增加而逐渐减小,当AI为10-7时,ZnO压敏电阻的α减小至7.4。这意味ZnO压敏电阻上的电压降明显增加,致使相关的电气设备遭受更多瞬态浪涌冲击的影响,严重威胁特高压电力系统的安全稳定运行。ZnO压敏电阻的非线性起源于晶粒之间的势垒区[5],该区域在整个晶界中的占比越大,则ZnO压敏电阻的α越大,JL越小。AI的增加将导致晶粒之间的势垒区减小,这是导致ZnO压敏电阻的α急剧减小、JL明显增大的根本原因。
图12和表5显示了厚晶间相区在整个晶界中的占比AⅢ对ZnO压敏电阻样品电气性能的影响。富含Bi2O3的厚晶界相占据着相邻2个晶粒的边缘区域,其具有较高的电阻率。然而,AⅢ的变化对ZnO压敏电阻的电气性能影响很小。随着AⅢ的增大,ZnO压敏电阻的JL和K仅有较小幅度的增加,E1mA和α的变化则可忽略不计。因此,可以忽略AⅢ的变化对ZnO压敏电阻电气特性造成的影响。
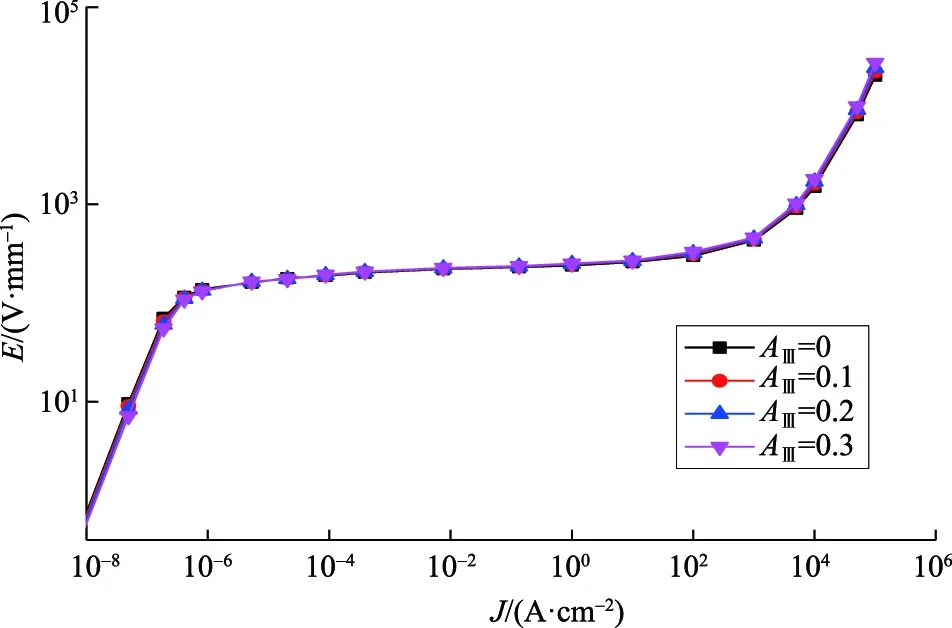
图12 AⅢ的变化对样品J-E特性曲线的影响Fig.12 Effect of changes of AⅢ on J-E characteristic curve of sample

表5 AⅢ的变化对样品电气性能的影响Tab.5 Effect of AⅢ changes on electrical properties of sample
厚晶界相区的电阻率较高,在AⅢ大小不变的情况下,厚晶界相电阻率ρⅢ的变化对ZnO压敏电阻样品电气性能的影响如图13和表6所示。ρⅢ的变化对ZnO压敏电阻的电气性能有明显影响。随着ρⅢ的降低,ZnO压敏电阻的JL明显增大。当ρⅢ减小至109Ω·m时,JL高达128 μA/cm2,严重超过了IEC 60099-4-2014规定的技术指标限值。

图13 ρⅢ的变化对样品J-E特性曲线的影响Fig.13 Effect of changes of ρⅢ on J-E characteristic curve of sample
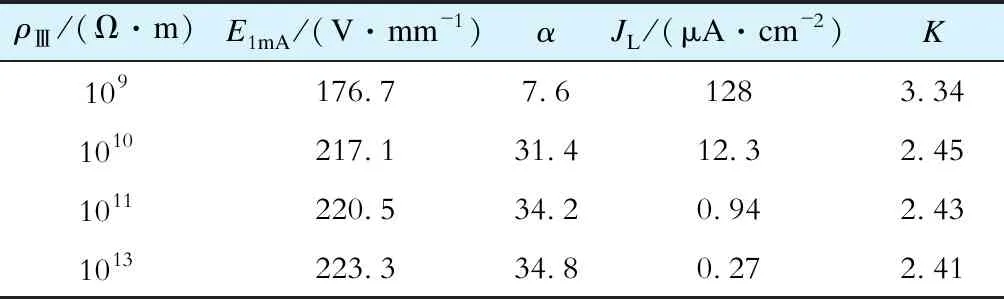
表6 ρⅢ的变化对样品电气性能的影响Tab.6 Effect of ρⅢ changes on electrical properties of sample
JL的大小不仅决定着ZnO压敏电阻在正常工作电压下的功率损耗,还决定其所能够承受的最大工作电压[18]。较大的JL会加速ZnO压敏电阻的热老化,使其电气性能进一步降低(如E1mA降低、JL增大等),电气性能的降低又将反向加速ZnO压敏电阻的老化[19]。这样的恶性循环将最终导致ZnO压敏电阻热失控,进而发生热崩溃或者热穿孔。在其两端外施电压时,JL总是寻找晶界数最少的路径通过ZnO压敏电阻;该路径将决定ZnO压敏电阻的E1mA和整体J-E特性。ρⅢ的减小将使更多的JL绕过晶粒之间的势垒区而通过厚晶界相区,致使ZnO压敏电阻的E1mA降低、α减小。ρⅢ减小至某一数值时,ZnO压敏电阻将失去非线性。由图13可知,ρⅢ的变化对ZnO压敏电阻在上升区域的影响非常小。E1mA的减小将导致K明显增大,从而抬高电力系统的绝缘水平和电网的造价成本[20-21]。因此,在研制高性能的ZnO压敏电阻时,应使ρⅢ维持在较高的数值。
4.5 Ni对ZnO压敏电阻电气性能的影响
Ni的变化对ZnO压敏电阻样品电气性能的影响如图14和表7所示。随着Ni的增大,E1mA和α明显增大,而JL和K则呈现出相反的变化趋势。这些参数的变化意味着ZnO压敏电阻电气性能的提高,有助于改善金属氧化物避雷器(metal oxide arrester,MOA)的保护性能。由φb的计算公式可知,晶界层的φb主要受Ni控制,与Ni的平方成正比,而与Nd成反比[22]。相关研究已经证明,ZnO压敏电阻的非线性主要受晶界层的φb控制,φb越高则其非线性越好,晶界层的击穿电压越大[13-14]。ZnO压敏电阻电气性能的改善可归因于Ni的增大提高了晶界层的φb,从而改善α,抑制JL增大。由图14可知,K的减小是由于Ni的增大提高了ZnO压敏电阻在预击穿区域的E1mA;因此,为了改善ZnO压敏电阻的电气性能,提高MOA对过电压的抑制能力,应尽可能提高Ni。
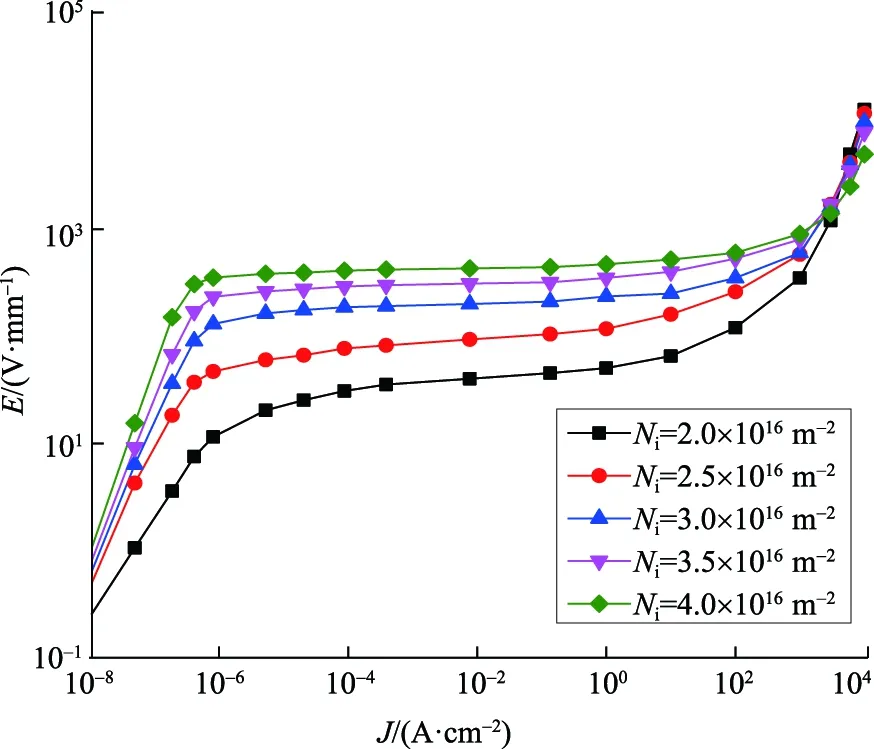
图14 Ni的变化对样品J-E特性曲线的影响Fig.14 Effect of Ni changes on J-E characteristic curve of sample

表7 Ni的变化对样品电气性能的影响Tab.7 Effect of Ni changes on electrical properties of sample
5 高梯度、低残压ZnO压敏电阻的研发策略
在第4章中,本文所分析的不同微观参数的变化对ZnO压敏电阻宏观电气特性的影响,都是在理想条件下进行的,在现实中很难实现。例如:通过提高ρⅢ或者减小AⅠ能有效地改善ZnO压敏电阻的电气性能,但ZnO晶粒在实际的液相辅助烧结过程中,其生长是随机和无序的,难以人为控制其微观参数的变化,也难以实现其微观参数的精确测量。
在提高ZnO压敏电阻E1mA的所有措施中,较容易实现且效果最为明显的措施是减小d。减小d的方法有很多,在过去的实际生产中,经常采用的方法是在ZnO压敏电阻配方中引入SiO2、Sb2O3等添加剂,或在烧结过程中通过降低烧结温度、缩短保温时间等措施来抑制ZnO晶粒的生长,从而达到减小d目的[4]。然而,上述方法对E1mA的改善效果并不理想。目前,最常用的方法是通过掺杂稀土元素以减小d,稀土元素的掺杂能够明显抑制晶粒的生长[22-24]。E1mA的提高对降低ZnO压敏电阻的K也具有明显的效果。K是表征ZnO压敏电阻保护效果的一个重要指标,也是以ZnO压敏电阻为核心元件的MOA的重要参数[22]。然而,在降低ZnO压敏电阻K的所有措施中,仅有降低ρ的措施能非常明显降低ZnO压敏电阻K,而对其他电气参数的变化无明显影响。在配方中引入三价的施主类型掺杂剂(如Al2O3、Ga2O3等)可以有效地降低ρ,从而维持ZnO压敏电阻的K在较低的水平[22]。在高梯度、低残压ZnO压敏电阻的研发过程中,应通过减小d和ρ作为研究的主要路线。当d和ρ减小到一定程度,再通过降低Nd、提高Ni等辅助措施进一步提高ZnO压敏电阻的E1mA,以降低残压比K。
6 结论
本文在新的晶界分区模型的基础上,根据研究条件对晶界层的等效电路模型进行了优化处理。根据晶界的真实导电机理和实际物理参数建立仿真模型,仿真分析压敏电阻在直流电压作用下的电气性能。通过分析不同微观参数的变化对ZnO压敏电阻宏观电气参数的影响,得出以下结论:
a)通过减小d、提高Ni或者降低Nd等微观参数,能够明显提高ZnO压敏电阻的E1mA,并降低残压比K。
b)在降低ZnO压敏电阻K值的所有措施中,仅有降低ρ的措施能在减小ZnO压敏电阻K值的同时,对其他电气参数无明显影响。根据仿真结果,本文提出高梯度、低残压的ZnO压敏电阻的研发策略,应以减小d、降低ρ作为主研究路线,以提高Ni、降低Nd等作为辅助措施。

